Статистические критерии 1 Распределение Стьюдента t-критерий Позволяет находить

Статистические критерии 1. Распределение Стьюдента (t-критерий) Позволяет находить генеральное среднее или проверять статистические гипотезы при малых объемах выборки. где В общем случае разного объема. и s 2 могут определяться по выборкам Квантили распределения Стьюдента зависят от объема выборки N или числа степеней свободы f = N-1, с которым определена дисперсия s 2.

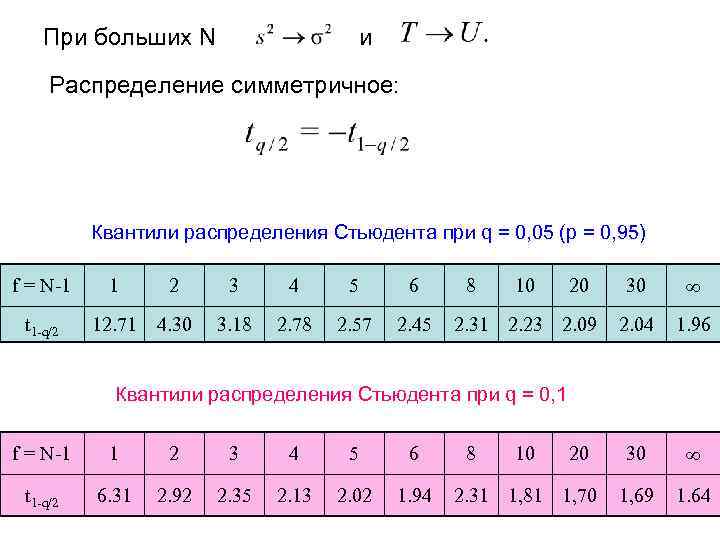При больших N и Распределение симметричное: Квантили распределения Стьюдента при q = 0, 05 (р = 0, 95) f = N-1 t 1 -q/2 1 2 12. 71 4. 30 3 4 5 6 3. 18 2. 78 2. 57 2. 45 8 10 20 2. 31 2. 23 2. 09 30 2. 04 1. 96 30 1, 69 1. 64 Квантили распределения Стьюдента при q = 0, 1 f = N-1 1 2 3 4 5 6 t 1 -q/2 6. 31 2. 92 2. 35 2. 13 2. 02 1. 94 8 10 20 2. 31 1, 81 1, 70

2. Распределение Фишера (F-критерий) Используется для проверки однородности двух выборочных дисперсий свободы f 1 и f 2 и определенных с числом степеней. Если то дисперсии однородны, то есть принадлежат одной генеральной совокупности. Если то гипотеза об однородности дисперсий отвергается на принятом уровне значимости.

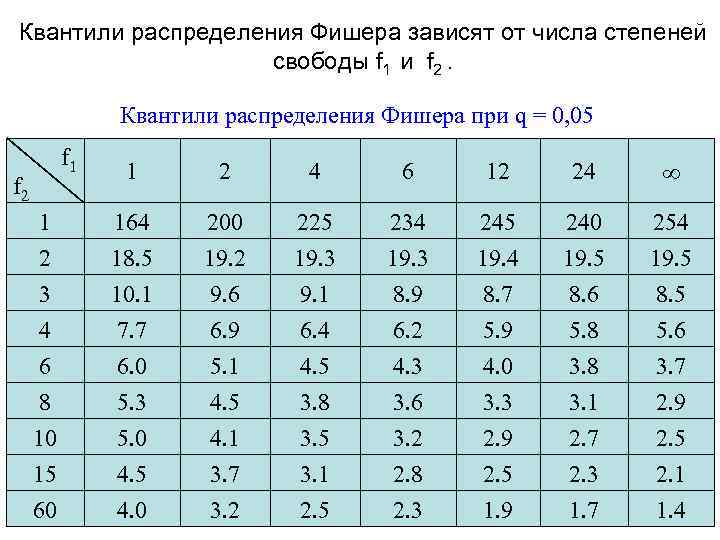Квантили распределения Фишера зависят от числa степеней свободы f 1 и f 2. Квантили распределения Фишера при q = 0, 05 f 1 1 2 4 6 12 24 1 2 164 18. 5 200 19. 2 225 19. 3 234 19. 3 245 19. 4 240 19. 5 254 19. 5 3 4 6 8 10 15 60 10. 1 7. 7 6. 0 5. 3 5. 0 4. 5 4. 0 9. 6 6. 9 5. 1 4. 5 4. 1 3. 7 3. 2 9. 1 6. 4 4. 5 3. 8 3. 5 3. 1 2. 5 8. 9 6. 2 4. 3 3. 6 3. 2 2. 8 2. 3 8. 7 5. 9 4. 0 3. 3 2. 9 2. 5 1. 9 8. 6 5. 8 3. 1 2. 7 2. 3 1. 7 8. 5 5. 6 3. 7 2. 9 2. 5 2. 1 1. 4 f 2

3. Распределение Пирсона ( - критерий) Используется для оценки генеральной дисперсии выборочной s 2. по Квантили распределения Пирсона зависят от числа степеней свободы f = N-1. Распределение несимметричное. Квантили распределения Пирсона при q = 0, 05 f 1 2 0. 0039 0. 103 3. 8 6. 00 3 4 5 7 0. 352 0. 71 1. 14 2. 17 7. 8 9. 5 11. 1 14. 1 10 20 3. 94 10. 90 18. 3 31. 4 30 16. 30 43. 4

4. Распределение Кохрена (G-критерий) Используется для проверки однородности k выборочных дисперсий, определенных с одинаковым числом степеней свободы f = N-1. Если то дисперсии однородны. Если то гипотеза об однородности дисперсий отвергается на принятом уровне значимости. Для однородных дисперсий общей наилучшей оценкой является дисперсия:

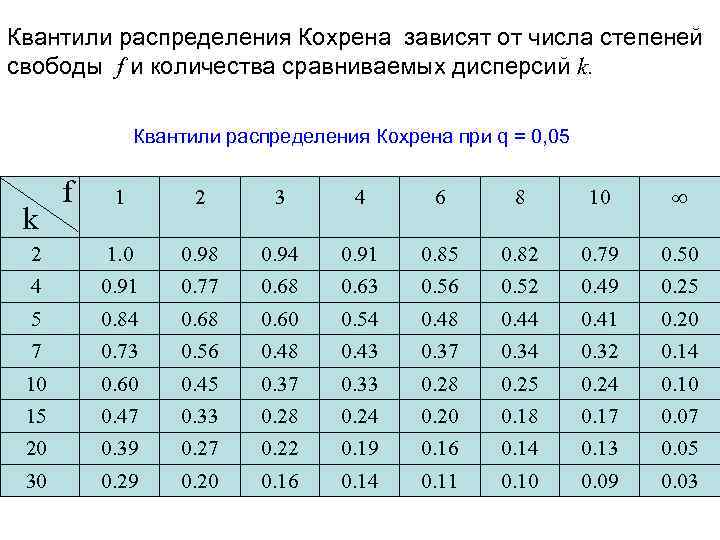Квантили распределения Кохрена зависят от числа степеней свободы f и количества сравниваемых дисперсий k. Квантили распределения Кохрена при q = 0, 05 f 1 2 3 4 6 8 10 2 1. 0 0. 98 0. 94 0. 91 0. 85 0. 82 0. 79 0. 50 4 0. 91 0. 77 0. 68 0. 63 0. 56 0. 52 0. 49 0. 25 5 0. 84 0. 68 0. 60 0. 54 0. 48 0. 44 0. 41 0. 20 7 0. 73 0. 56 0. 48 0. 43 0. 37 0. 34 0. 32 0. 14 10 0. 60 0. 45 0. 37 0. 33 0. 28 0. 25 0. 24 0. 10 15 0. 47 0. 33 0. 28 0. 24 0. 20 0. 18 0. 17 0. 07 20 0. 39 0. 27 0. 22 0. 19 0. 16 0. 14 0. 13 0. 05 30 0. 29 0. 20 0. 16 0. 14 0. 11 0. 10 0. 09 0. 03 k

5. - распределение ( -критерий) Используется для проверки однородности наблюдений в выборке и отсеивания грубых ошибок (промахов, выбросов). Хкр - крайний элемент в выборке. Квантили распределения зависят от объема выборки и принятого уровня значимости. Квантили - распределения при q = 0, 05 3 4 5 6 7 8 9 10 15 20 N 1 -q 1. 41 1. 69 1. 87 2. 00 2. 09 2. 17 2. 24 2. 29 2. 49 2. 62

Все рассмотренные распределения предполагают нормальность закона распределения случайной величины. При малых выборках проверку нормальности распределения можно провести по критериям согласия, основанным на выборочных асимметрии, эксцессе и их дисперсиях: Критерии согласия: Если и , то распределение можно считать нормальным.

Сравнение средних Задача сравнения средних может быть сведена к проверке нулевой гипотезы и решена с помощью критерия Стьюдента. Пусть имеем две однотипные СВ, заданные выборками: X ( x 1, x 2, . . x. N ) объемом N; Y ( y 1, y 2, . . . y. M ) объемом M. Требуется проверить гипотезу: 1. Вычисляются и их дисперсии определенные с числом степеней свободы fx = N – 1; 2. fy = M – 1. 2. Вводится новая СВ 3. Выполняется проверка однородности дисперсий

4. Если дисперсии однородны, то их общей оценкой будет дисперсия: Тогда Если то нулевая гипотеза не отвергается и Если то нулевая гипотеза отвергается и

Если дисперсии неоднородны: Определив квантили t. Т для fx и для Если fy, рассчитываем: то нулевая гипотеза отвергается.