СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И ДОСТОВЕРНОСТЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК ЦЕЛИ

СТАТИСТИЧЕСКИЕ ГИПОТЕЗЫ И ДОСТОВЕРНОСТЬ СТАТИСТИЧЕСКИХ ХАРАКТЕРИСТИК

ЦЕЛИ: 1. Ознакомиться с понятием «статистическая гипотеза» . 2. Изучить основной принцип проверки статистических гипотез. 3. Изучить алгоритм выбора критерия для сравнения двух средних арифметических генеральных совокупностей.

1. Статистические гипотезы (понятие, цель). 2. Проверка статистических гипотез и ее основные этапы. 3. Алгоритм выбора критерия для сравнения двух средних арифметических генеральных совокупностей.

Гипотеза - это научное предположение, выдвигаемое для объяснения к. -л. явления и требующая проверки на опыте и теоретического обоснования, чтобы стать достоверной научной истиной Статистической гипотезой наз. проверяемое математическими методами предположение относительно статистических характеристик результатов измерений. (обозначение гипотезы: Н) Н 0 - нулевая гипотеза, Н 1 - конкурирующая гипотеза

Проверка статистических гипотез Процедура проверки гипотез сводится: • выдвигаются две гипотезы Н 0, Н 1 • по выборочным данным вычисляется значение некоторой величины - Критерий (K) • Кнабл < > Ккрит (из табл. ) какую выбрать гипотезу? Область принятия гипотезы Н 0 Ккрит Критическая область Н 1 (схема односторонней критической области) К 1 крит К 2 крит Критическая область Область принятия гипотезы (схема двухсторонней критической области) Критическая Область

Н 0/Н 0 – приняли за достоверную Н 0 и она верна Н 1/Н 1 – приняли за достоверную Н 1 и она верна 1) Ошибки проверке гипотез Н 1/Н 0 – приняли за достоверную Н 1, а верна Н 0 (ошибка 1 -го рода) 2) Н 0/Н 1 – приняли за достоверную Н 0, а верна Н 1 (ошибка 2 -го рода) α – уровень значимости – вероятность того, что мы приняли за достоверную Н 1, а верна Н 0 Р(Н 1/Н 0) = α (0, 1; 0, 05; 0, 01; 0, 001)

Критерии для проверки гипотез 1. Параметрические 2. Непараметрические

Основные этапы проверки статистических гипотез Выбор критерия: 1. Формулировка гипотез (Н 0 и Н 1) 1. От объема выборки (малая, большая) 2. Выбор уровня значимости из ряда 2. От закона распределения α 3. От степени 0, 001) (0, 1; 0, 05; 0, 01; зависимости выборок (зависимые или независимые) 3. Определение выборочного значения 4. Известны или неизвестны расчета) статистических характеристик (из 2 генеральные дисперсии ( ген) 4. Выбор критерия для проверки 5. Одинаковы или различны статистических гипотез генеральные дисперсии 6. Возможна ли количественная или 5. Сравнение расчетного значения критерия качественная оценка (Кнабл) с критическим (Ккрит) для рассматриваемого явленияиз гипотез выбранного α и принятия одной

Выбор критерия • Известны генеральные дисперсии ( 2 ген) (Z – критерий) • Неизвестны 2 ген Z – критерий используется как приближенный

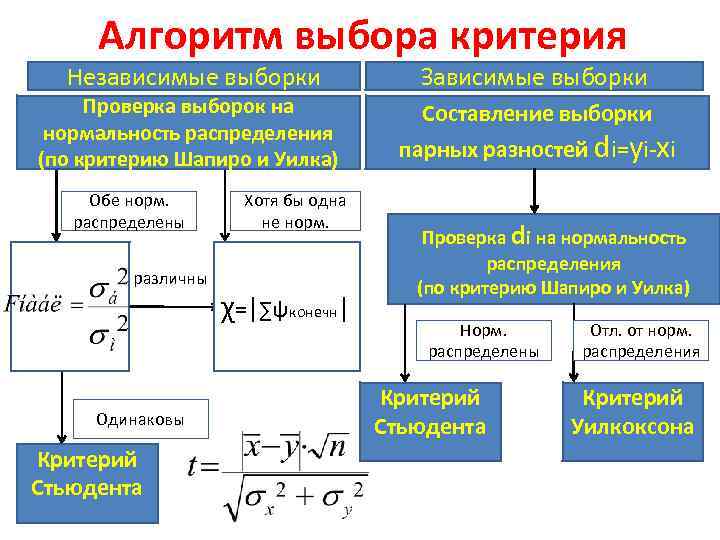Алгоритм выбора критерия Независимые выборки Зависимые выборки Проверка выборок на нормальность распределения (по критерию Шапиро и Уилка) Составление выборки Обе норм. распределены Сравнение их различны дисперсий по критерию Фишера Одинаковы Критерий Стьюдента Хотя бы одна не норм. Критерий Вандер =|∑ψконечн| Вардена χ парных разностей di=yi-xi Проверка di на нормальность распределения (по критерию Шапиро и Уилка) Норм. распределены Критерий Стьюдента Отл. от норм. распределения Критерий Уилкоксона