Статистическая взаимосвязь.ppt
- Количество слайдов: 21
 Статистическая взаимосвязь социальноправовых явлений Понятие о статистической взаимосвязи социально-правовых явлений. Параметрические и Непараметрические методы исследования статистической взаимосвязи
Статистическая взаимосвязь социальноправовых явлений Понятие о статистической взаимосвязи социально-правовых явлений. Параметрические и Непараметрические методы исследования статистической взаимосвязи
 Статистическая взаимосвязь социально-правовых явлений n Понятие о статистической взаимосвязи социально-правовых явлений n Непараметрические методы исследования статистической взаимосвязи n Параметрические методы исследования статистической взаимосвязи
Статистическая взаимосвязь социально-правовых явлений n Понятие о статистической взаимосвязи социально-правовых явлений n Непараметрические методы исследования статистической взаимосвязи n Параметрические методы исследования статистической взаимосвязи
 Понятие о статистической взаимосвязи явлений и процессов Функциональной зависимостью некоторой величины Y от нескольких переменных x 1, x 2, …, xn называется связь, в соответствии с которой результативная величина Y зависит только от набора факторов x 1, x 2, …, xn и ни от чего больше Статистической (стохастической) зависимостью некоторой стохастической величины Y от нескольких переменных x 1, x 2, …, xn называется связь, в которой результативная величина Y может принимать любые значения с некоторыми вероятностями, но её среднее значение или иные статистические характеристики изменяются по определённому закону
Понятие о статистической взаимосвязи явлений и процессов Функциональной зависимостью некоторой величины Y от нескольких переменных x 1, x 2, …, xn называется связь, в соответствии с которой результативная величина Y зависит только от набора факторов x 1, x 2, …, xn и ни от чего больше Статистической (стохастической) зависимостью некоторой стохастической величины Y от нескольких переменных x 1, x 2, …, xn называется связь, в которой результативная величина Y может принимать любые значения с некоторыми вероятностями, но её среднее значение или иные статистические характеристики изменяются по определённому закону
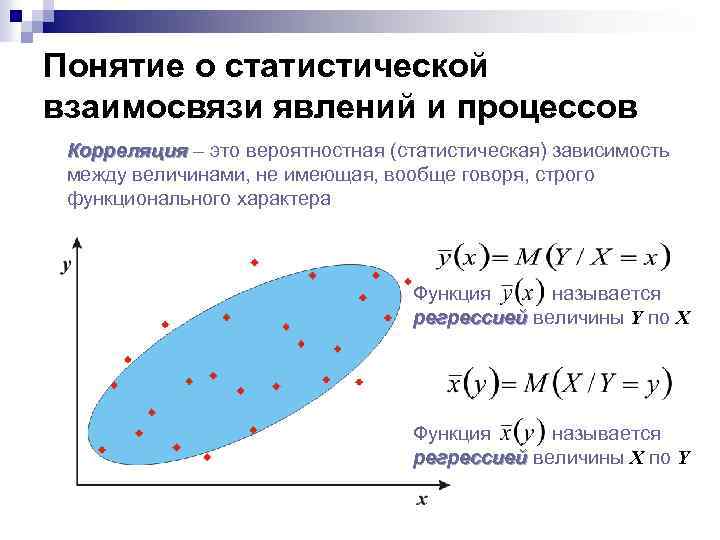 Понятие о статистической взаимосвязи явлений и процессов Корреляция – это вероятностная (статистическая) зависимость между величинами, не имеющая, вообще говоря, строго функционального характера Функция называется регрессией величины Y по X Функция называется регрессией величины X по Y
Понятие о статистической взаимосвязи явлений и процессов Корреляция – это вероятностная (статистическая) зависимость между величинами, не имеющая, вообще говоря, строго функционального характера Функция называется регрессией величины Y по X Функция называется регрессией величины X по Y
 Корреляционный анализ – это метод обработки данных статистического наблюдения, позволяющий найти форму, направление и величину взаимной связи показателей По форме взаимной связи: q линейная q нелинейная По направлению взаимной связи: q прямая q обратная
Корреляционный анализ – это метод обработки данных статистического наблюдения, позволяющий найти форму, направление и величину взаимной связи показателей По форме взаимной связи: q линейная q нелинейная По направлению взаимной связи: q прямая q обратная
 Задачи и условия применения корреляционного анализа Задачи применения корреляционного анализа • установление аналитического выражения (формы и направления) взаимной связи явлений или процессов; • определения степени (тесноты) взаимной связи между исследуемыми величинами; • оценка ошибок статистических показателей. Условия применения корреляционного анализа • наличие данных достаточно большой совокупности; • качественная однородность исследуемой совокупности; • совокупность результативного Y и факторного X признаков распределена по нормальному закону
Задачи и условия применения корреляционного анализа Задачи применения корреляционного анализа • установление аналитического выражения (формы и направления) взаимной связи явлений или процессов; • определения степени (тесноты) взаимной связи между исследуемыми величинами; • оценка ошибок статистических показателей. Условия применения корреляционного анализа • наличие данных достаточно большой совокупности; • качественная однородность исследуемой совокупности; • совокупность результативного Y и факторного X признаков распределена по нормальному закону
 Коэффициент корреляции – числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь В зависимости от показателя (качественный или количественный) и от его шкалы измерения (номинальная, ранговая или метрическая) используются различные методы расчёта коэффициента корреляции. различают: q параметрические – методы, использующие количественные характеристики параметров распределения (средние, дисперсия и т. п. ); q непараметрические – методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения параметров распределения.
Коэффициент корреляции – числовая характеристика совместного распределения двух случайных величин, выражающая их взаимосвязь В зависимости от показателя (качественный или количественный) и от его шкалы измерения (номинальная, ранговая или метрическая) используются различные методы расчёта коэффициента корреляции. различают: q параметрические – методы, использующие количественные характеристики параметров распределения (средние, дисперсия и т. п. ); q непараметрические – методы, с помощью которых можно измерить связь между явлениями, не используя при этом количественные значения параметров распределения.
 Непараметрические методы определения статистической связи коэффициент ассоциации и коэффициент контингенции – вычисляются при исследовании тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков; коэффициент взаимной сопряжённости Пирсона и Чупрова – используется когда необходимо оценить тесноту связи между качественными признаками, которые могут принимать любое число вариантов значений; ранговые коэффициенты корреляции – коэффициенты, в основу вычисления которых положен принцип нумерации значений статистического ряда;
Непараметрические методы определения статистической связи коэффициент ассоциации и коэффициент контингенции – вычисляются при исследовании тесноты связи между качественными признаками, каждый из которых представлен в виде альтернативных признаков; коэффициент взаимной сопряжённости Пирсона и Чупрова – используется когда необходимо оценить тесноту связи между качественными признаками, которые могут принимать любое число вариантов значений; ранговые коэффициенты корреляции – коэффициенты, в основу вычисления которых положен принцип нумерации значений статистического ряда;
 Коэффициент ассоциации и коэффициент контингенции Группы 1 2 Признаки 1 2 a b c d Сумма a + c Сумма Коэффициент ассоциации: a + b c + d b + d Коэффициент контингенции: Примечание: для одних и тех же данных коэффициент контингенции всегда меньше коэффициента ассоциации.
Коэффициент ассоциации и коэффициент контингенции Группы 1 2 Признаки 1 2 a b c d Сумма a + c Сумма Коэффициент ассоциации: a + b c + d b + d Коэффициент контингенции: Примечание: для одних и тех же данных коэффициент контингенции всегда меньше коэффициента ассоциации.
 Коэффициент взаимной сопряжённости Пирсона и Чупрова Группы признака А Группы признака В Итого В 1 В 2 В 3 А 1 f 12 f 13 А 2 f 21 f 22 f 23 А 3 f 31 f 32 f 33 Итого
Коэффициент взаимной сопряжённости Пирсона и Чупрова Группы признака А Группы признака В Итого В 1 В 2 В 3 А 1 f 12 f 13 А 2 f 21 f 22 f 23 А 3 f 31 f 32 f 33 Итого
 Коэффициент взаимной сопряжённости Пирсона и Чупрова Коэффициент Пирсона: Пирсона , где – средний показатель квадратической сопряжённости. Коэффициент Чупрова: Чупрова , где K 1, K 2 – число возможных значений статистических величин по столбцам и строкам статистической таблицы
Коэффициент взаимной сопряжённости Пирсона и Чупрова Коэффициент Пирсона: Пирсона , где – средний показатель квадратической сопряжённости. Коэффициент Чупрова: Чупрова , где K 1, K 2 – число возможных значений статистических величин по столбцам и строкам статистической таблицы
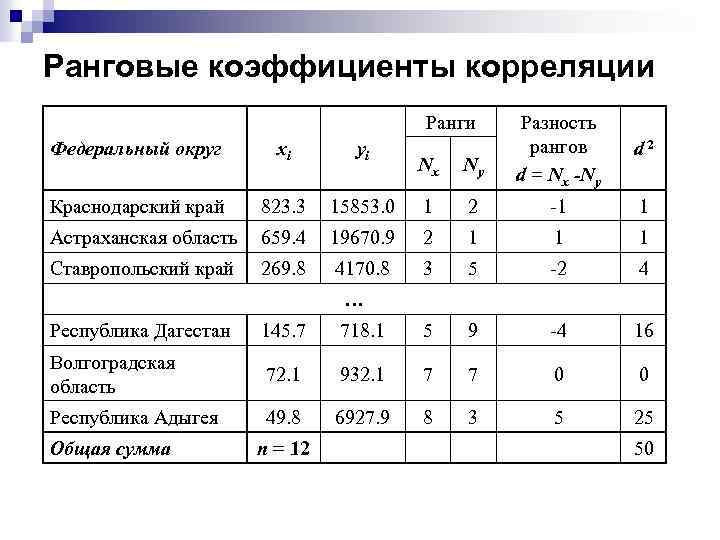 Ранговые коэффициенты корреляции Ранги Федеральный округ xi yi Краснодарский край 823. 3 Астраханская область Ставропольский край Разность рангов d = Nx -Ny d 2 Nx Ny 15853. 0 1 2 -1 1 659. 4 19670. 9 2 1 1 1 269. 8 4170. 8 3 5 -2 4 … Республика Дагестан 145. 7 718. 1 5 9 -4 16 Волгоградская область 72. 1 932. 1 7 7 0 0 Республика Адыгея 49. 8 6927. 9 8 3 5 25 Общая сумма n = 12 50
Ранговые коэффициенты корреляции Ранги Федеральный округ xi yi Краснодарский край 823. 3 Астраханская область Ставропольский край Разность рангов d = Nx -Ny d 2 Nx Ny 15853. 0 1 2 -1 1 659. 4 19670. 9 2 1 1 1 269. 8 4170. 8 3 5 -2 4 … Республика Дагестан 145. 7 718. 1 5 9 -4 16 Волгоградская область 72. 1 932. 1 7 7 0 0 Республика Адыгея 49. 8 6927. 9 8 3 5 25 Общая сумма n = 12 50
 Ранговые коэффициенты корреляции Коэффициент корреляции рангов Спирмена – основан на рассмотрении разности рангов значений результативного и факторного признаков Коэффициент конкордации (согласованности) рангов согласованности Кендела – используется для определения меры тесноты связи между произвольным числом (n > 2) исследуемых признаков где S – сумма квадратов отклонений суммы рангов от их средней величины; m – число ранжируемых признаков, n – число наблюдений
Ранговые коэффициенты корреляции Коэффициент корреляции рангов Спирмена – основан на рассмотрении разности рангов значений результативного и факторного признаков Коэффициент конкордации (согласованности) рангов согласованности Кендела – используется для определения меры тесноты связи между произвольным числом (n > 2) исследуемых признаков где S – сумма квадратов отклонений суммы рангов от их средней величины; m – число ранжируемых признаков, n – число наблюдений
 Параметрические методы определения статистической связи Коэффициент Фехнера – основан на определении корреляции знаков и используется в случае, когда наблюдаемая совокупность представлена небольшим числом исходных данных где С – число совпадений знаков; H – число несовпадений знаков; С + H – общее число наблюдаемых единиц.
Параметрические методы определения статистической связи Коэффициент Фехнера – основан на определении корреляции знаков и используется в случае, когда наблюдаемая совокупность представлена небольшим числом исходных данных где С – число совпадений знаков; H – число несовпадений знаков; С + H – общее число наблюдаемых единиц.
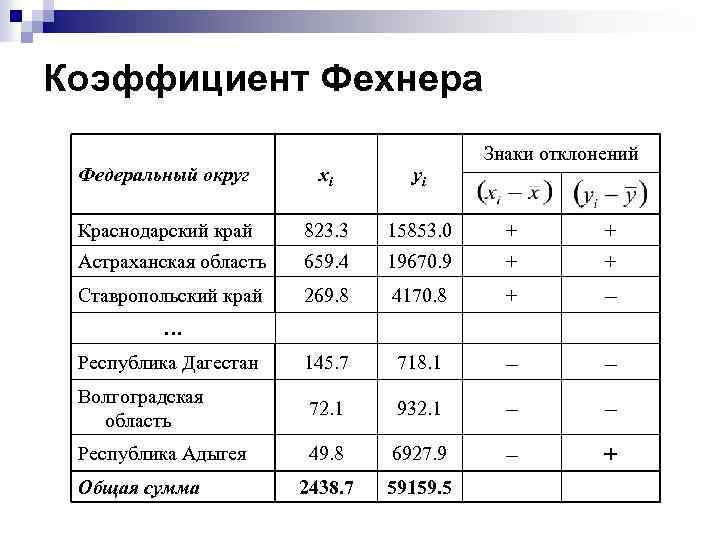 Коэффициент Фехнера Знаки отклонений Федеральный округ xi yi Краснодарский край 823. 3 15853. 0 + + Астраханская область 659. 4 19670. 9 + + Ставропольский край 269. 8 4170. 8 + – Республика Дагестан 145. 7 718. 1 – – Волгоградская область 72. 1 932. 1 – – Республика Адыгея 49. 8 6927. 9 – + 2438. 7 59159. 5 … Общая сумма
Коэффициент Фехнера Знаки отклонений Федеральный округ xi yi Краснодарский край 823. 3 15853. 0 + + Астраханская область 659. 4 19670. 9 + + Ставропольский край 269. 8 4170. 8 + – Республика Дагестан 145. 7 718. 1 – – Волгоградская область 72. 1 932. 1 – – Республика Адыгея 49. 8 6927. 9 – + 2438. 7 59159. 5 … Общая сумма
 Линейный коэффициент корреляции – применяется для оценки тесноты взаимной связи между количественными результативным Y и факторным X признаками в случае их линейной зависимости где sx, sy – среднеквадратические отклонения, соответственно, результативного Y и факторного X признаков.
Линейный коэффициент корреляции – применяется для оценки тесноты взаимной связи между количественными результативным Y и факторным X признаками в случае их линейной зависимости где sx, sy – среднеквадратические отклонения, соответственно, результативного Y и факторного X признаков.
 Основные свойства линейного коэффициента корреляции 1. Коэффициент корреляции изменяется в интервале (-1, 1), или -1 < rxy < 1 2. Если между факторами x и y взаимосвязь отсутствует, то rxy = 0 3. Условие |rxy| = 1 является необходимым и достаточным для существования линейной функциональной зависимости между x и y Следствие: чем ближе |rxy| к единице, тем ближе корреляционная зависимость между величинами x и y к линейной функциональной зависимости, и, наоборот, чем выше степень линейной корреляционной зависимости между величинами x и y, тем ближе |rxy| к единице
Основные свойства линейного коэффициента корреляции 1. Коэффициент корреляции изменяется в интервале (-1, 1), или -1 < rxy < 1 2. Если между факторами x и y взаимосвязь отсутствует, то rxy = 0 3. Условие |rxy| = 1 является необходимым и достаточным для существования линейной функциональной зависимости между x и y Следствие: чем ближе |rxy| к единице, тем ближе корреляционная зависимость между величинами x и y к линейной функциональной зависимости, и, наоборот, чем выше степень линейной корреляционной зависимости между величинами x и y, тем ближе |rxy| к единице
 Линейный коэффициент корреляции Качественная интерпретация коэффициента корреляции (таблица Чеддока) Значения rxy Интерпретация связи rxy = 0 0 < rxy < 0. 25 < rxy < 0. 50 < rxy < 0. 75 < rxy < 1. 0 rxy = 1 отсутствует слабая умеренная значительная сильная функциональная
Линейный коэффициент корреляции Качественная интерпретация коэффициента корреляции (таблица Чеддока) Значения rxy Интерпретация связи rxy = 0 0 < rxy < 0. 25 < rxy < 0. 50 < rxy < 0. 75 < rxy < 1. 0 rxy = 1 отсутствует слабая умеренная значительная сильная функциональная
 Парная линейная регрессия представляет собой математическую модель, в которой усреднённое значение результативного Y признака (зависимая переменная) рассматривается как линейная функция факторного X признака (независимая переменная) где – коэффициент регрессии; – постоянная регрессии.
Парная линейная регрессия представляет собой математическую модель, в которой усреднённое значение результативного Y признака (зависимая переменная) рассматривается как линейная функция факторного X признака (независимая переменная) где – коэффициент регрессии; – постоянная регрессии.
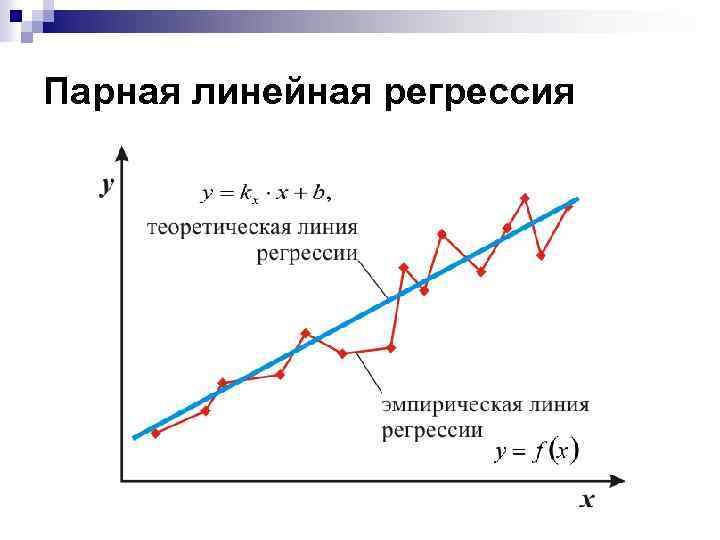 Парная линейная регрессия
Парная линейная регрессия
 Основные свойства коэффициента линейной регрессии 1. Чем выше значение коэффициента регрессии, тем сильнее проявляется влияние фактора x на фактор y 2. Положительное значение kx свидетельствует о прямой связи между факторами, отрицательное – об обратной
Основные свойства коэффициента линейной регрессии 1. Чем выше значение коэффициента регрессии, тем сильнее проявляется влияние фактора x на фактор y 2. Положительное значение kx свидетельствует о прямой связи между факторами, отрицательное – об обратной


