1. Статистическая обработка данных.pptx
- Количество слайдов: 22

Статистическая обработка данных психологопедагогического обследования Лектор: Фатихова Лидия Фаварисовна, кандидат педагогических наук, доцент кафедры специальной педагогики и психологии ФГБОУ ВПО «Башкирский государственный педагогический университет им. М. Акмуллы»

План лекции: 1. Обоснование необходимости графической презентации и проведения статистической обработки данных. 2. Графическая презентация данных массового обследования (гистограммы, круговые диаграммы, графики). 3. Статистические критерии: назначение, вычисление.

1. Обоснование необходимости графической презентации и проведения статистической обработки данных Научно-исследовательская деятельность становится одним из важнейших направлений профессиональной деятельности педагога, вообще, и дефектолога, в частности. В связи с этим педагогу-дефектологу необходимо проводить исследование образовательных процессов и психического развития лиц с ОВЗ. После проведения исследования становится необходимым презентовать полученные данные для того, чтобы поделиться этой информацией с коллегами и другими участниками коррекционно-образовательного процесса.

Одними из основных средств презентации результатов исследования являются построение диаграмм и использование средств математической статистики.

2. Графическая презентация данных массового обследования (гистограммы, круговые диаграммы, графики) Когда речь идет о динамике, т. е. изменении какогото массового явления, например, изменении количества детей с девиантным (общественно опасным) поведением, на основании учета количества этих детей, проживающих на территории деятельности комиссии можно отразить для наглядности как в виде графика, так и в виде столбиковой диаграммы (гистограммы).
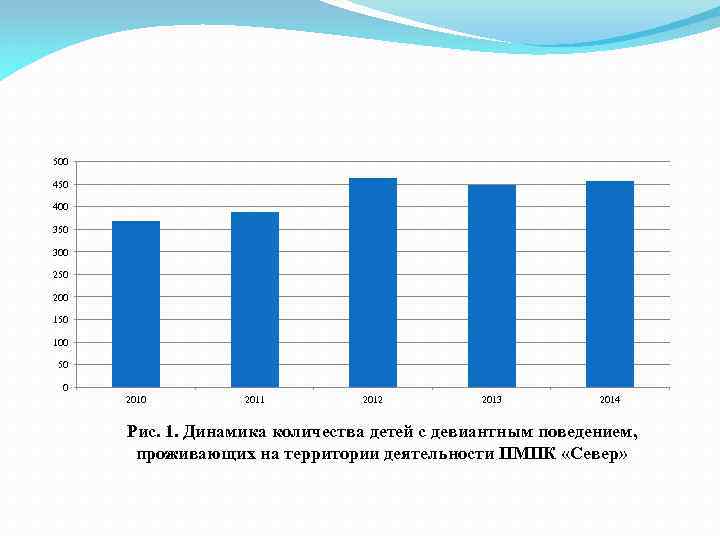
500 450 400 350 300 250 200 150 100 50 0 2011 2012 2013 2014 Рис. 1. Динамика количества детей с девиантным поведением, проживающих на территории деятельности ПМПК «Север»
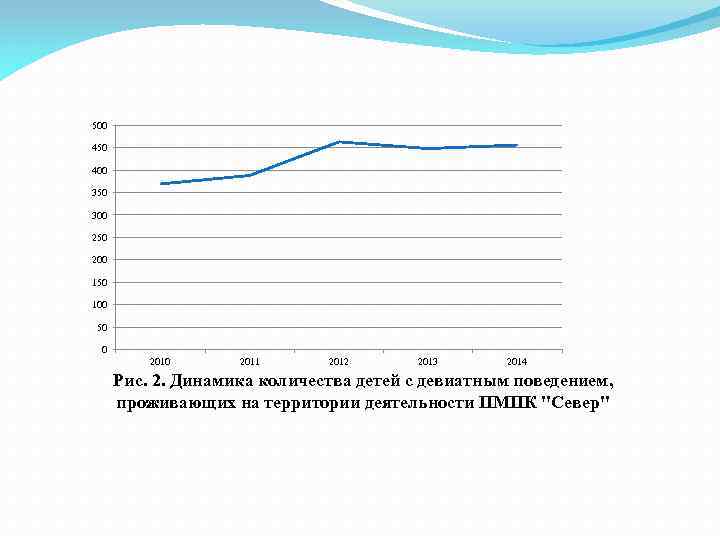
500 450 400 350 300 250 200 150 100 50 0 2011 2012 2013 2014 Рис. 2. Динамика количества детей с девиатным поведением, проживающих на территории деятельности ПМПК "Север"

Когда стоит задача сравнить группы (например, районы или категории лиц с ОВЗ) по характеру и интенсивности динамики какого-то явления, то это также можно изобразить в виде графика или гистограммы.
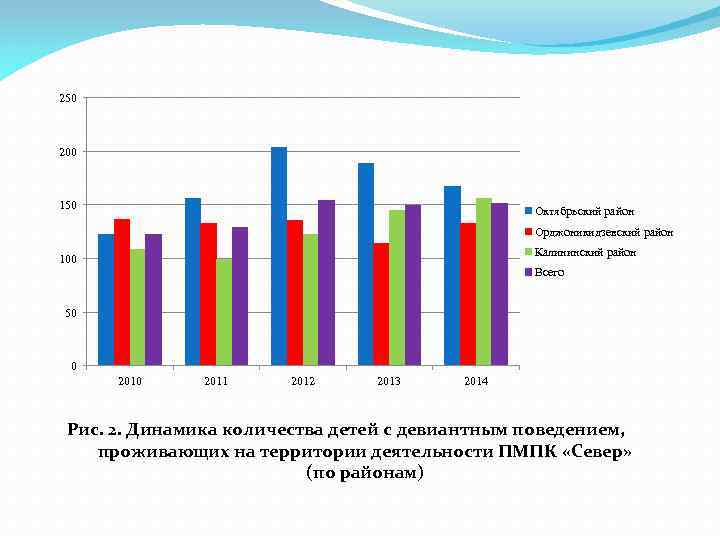
250 200 150 Октябрьский район Орджоникидзевский район Калининский район 100 Всего 50 0 2011 2012 2013 2014 Рис. 2. Динамика количества детей с девиантным поведением, проживающих на территории деятельности ПМПК «Север» (по районам)
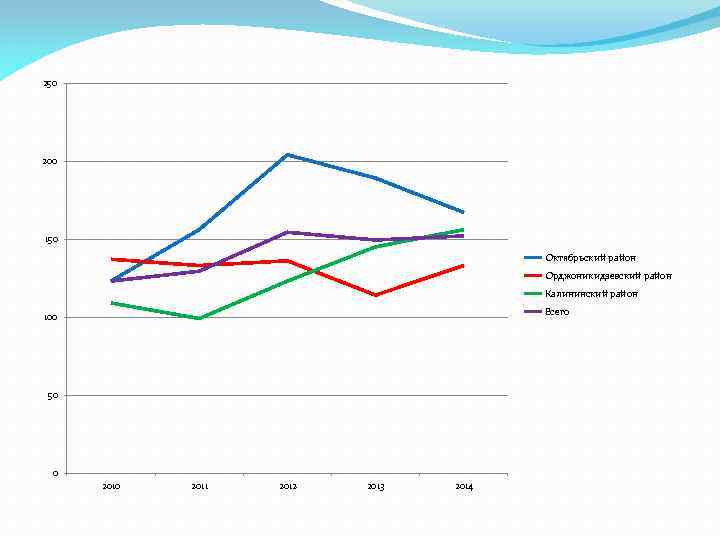
250 200 150 Октябрьский район Орджоникидзевский район Калининский район Всего 100 50 0 2011 2012 2013 2014
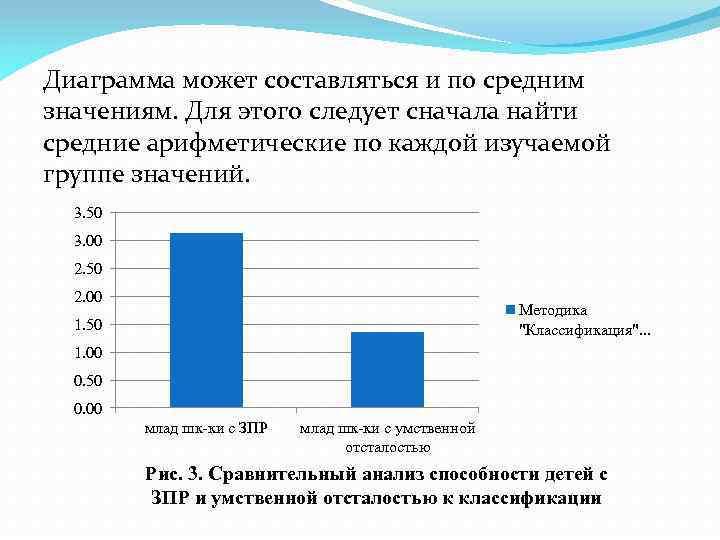
Диаграмма может составляться и по средним значениям. Для этого следует сначала найти средние арифметические по каждой изучаемой группе значений. 3. 50 3. 00 2. 50 2. 00 Методика "Классификация". . . 1. 50 1. 00 0. 50 0. 00 млад шк-ки с ЗПР млад шк-ки с умственной отсталостью Рис. 3. Сравнительный анализ способности детей с ЗПР и умственной отсталостью к классификации
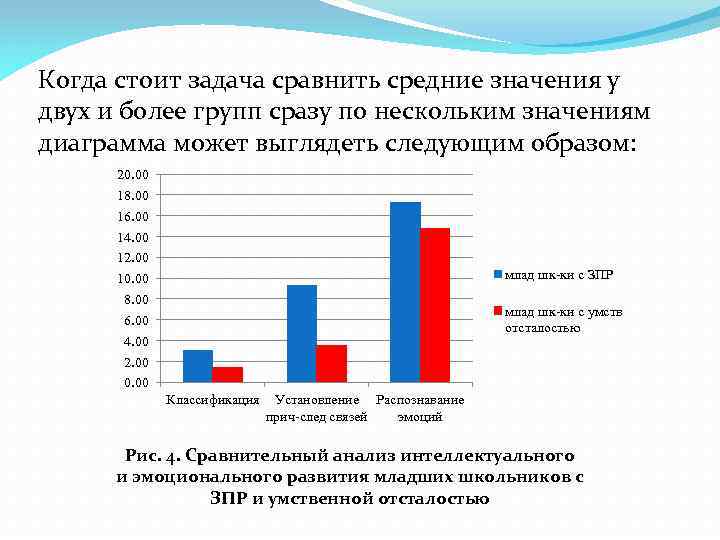
Когда стоит задача сравнить средние значения у двух и более групп сразу по нескольким значениям диаграмма может выглядеть следующим образом: 20. 00 18. 00 16. 00 14. 00 12. 00 10. 00 8. 00 6. 00 4. 00 2. 00 0. 00 млад шк-ки с ЗПР млад шк-ки с умств отсталостью Классификация Установление Распознавание прич-след связей эмоций Рис. 4. Сравнительный анализ интеллектуального и эмоционального развития младших школьников с ЗПР и умственной отсталостью
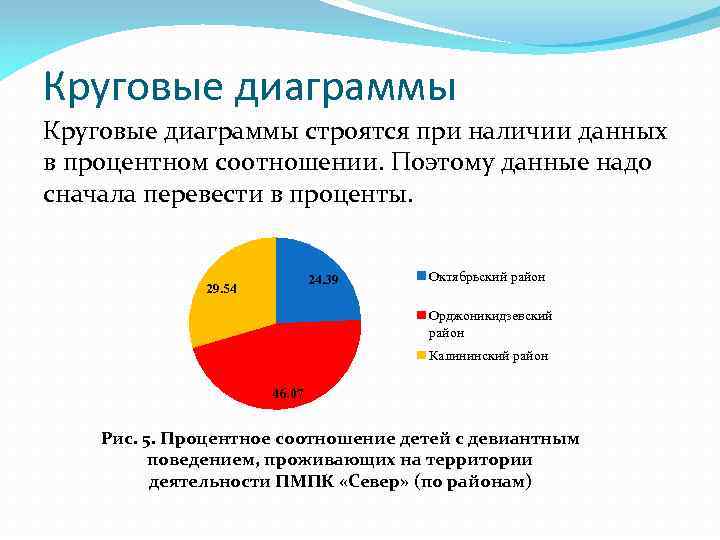
Круговые диаграммы строятся при наличии данных в процентном соотношении. Поэтому данные надо сначала перевести в проценты. 24. 39 29. 54 Октябрьский район Орджоникидзевский район Калининский район 46. 07 Рис. 5. Процентное соотношение детей с девиантным поведением, проживающих на территории деятельности ПМПК «Север» (по районам)

3. Статистические критерии: назначение, вычисление Среди задач, которые можно решать в практике психологопедагогических исследований средствами математической статистики можно выделить следующие: 1) выявления различий в уровне исследуемого признака (например стоит задача выявить различия в уровне развития мышлений у детей с ЗПР и ОНР); 2) оценка сдвига значений исследуемого признака (например, стоит задача в выявлении эффективности предпринятого коррекционного воздействия); 3) выявление взаимосвязи между признаками(например, стоит задача выявить, существует ли взаимосвязь между уровнем развития речи и мышления у детей с отклонениями в развитии); 4) выявление влияния какого-либо фактора на данные (например, стоит задача выявить, влияет ли тип семейного воспитания на проявления нарушений эмоциональной сферы у детей с ОВЗ).
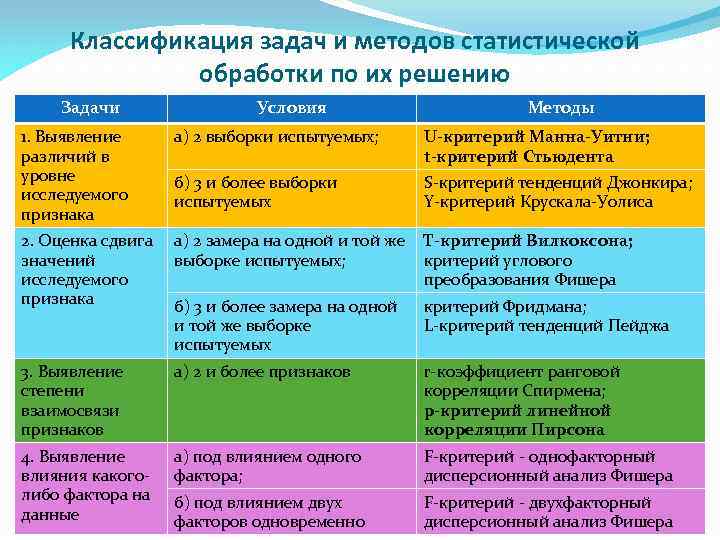
Классификация задач и методов статистической обработки по их решению Задачи Условия Методы 1. Выявление различий в уровне исследуемого признака а) 2 выборки испытуемых; U-критерий Манна-Уитни; t-критерий Стьюдента б) 3 и более выборки испытуемых S-критерий тенденций Джонкира; Y-критерий Крускала-Уолиса 2. Оценка сдвига значений исследуемого признака а) 2 замера на одной и той же Т-критерий Вилкоксона; выборке испытуемых; критерий углового преобразования Фишера б) 3 и более замера на одной и той же выборке испытуемых критерий Фридмана; L-критерий тенденций Пейджа 3. Выявление степени взаимосвязи признаков а) 2 и более признаков r-коэффициент ранговой корреляции Спирмена; p-критерий линейной корреляции Пирсона 4. Выявление влияния какоголибо фактора на данные а) под влиянием одного фактора; F-критерий - однофакторный дисперсионный анализ Фишера б) под влиянием двух факторов одновременно F-критерий - двухфакторный дисперсионный анализ Фишера

1. Среднее значение или среднее арифметическое (в математике и статистике) — одна из наиболее распространённых мер центральной тенденции, представляющая собой сумму всех зафиксированных значений, делённую на их количество. Среднее значение рассчитывается, как правило, для проведения дальнейшей обработки данных.
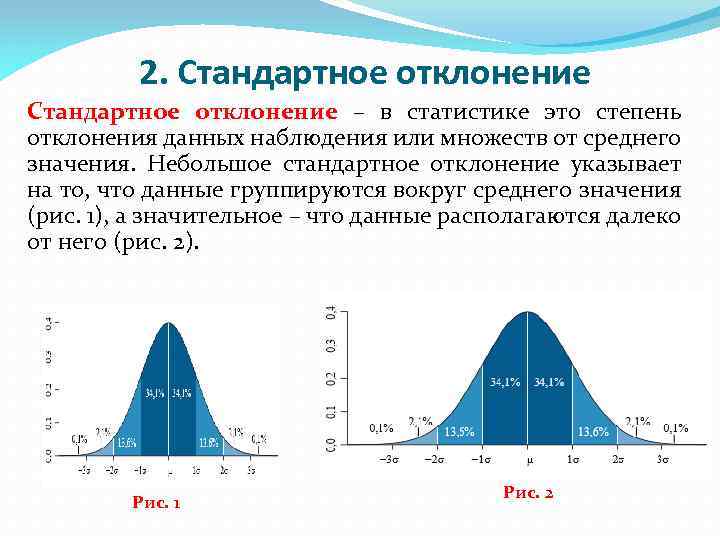
2. Стандартное отклонение – в статистике это степень отклонения данных наблюдения или множеств от среднего значения. Небольшое стандартное отклонение указывает на то, что данные группируются вокруг среднего значения (рис. 1), а значительное – что данные располагаются далеко от него (рис. 2). Рис. 1 Рис. 2

3. t-критерий Стьюдента — общее название для класса методов статистической проверки гипотез, основанных на распределении Стьюдента. Наиболее частые случаи применения t-критерия связаны с проверкой равенства средних значений в двух выборках. Это параметрический критерий, т. е. он основан на вычислении среднего значения и стандартного отклонения.

4. U-критерий Манна-Уитни - статистический критерий, используемый для оценки различий между двумя независимыми выборками по уровню какого-либо признака, измеренного количественно. Позволяет выявлять различия в значении параметра между малыми выборками. Это непараметрический критерий, т. е. он не основан на вычислении среднего значения и стандартного отклонения.

5. Т-критерий Вилкоксона - статистический критерий, используемый для сопоставления показателей в двух разных условиях на одной и той же выборке испытуемых. Он позволяет установить направленность изменений и их выраженность, например, насколько сильно повлияло то или иное воздействие или условие на степень выраженности измеренного качества.

6. Корреляционные методы Выделяют 2 основных метода выявления корреляционной зависимости переменных – коэффициент ранговой корреляции Спирмена (r -коэффиент) и коэффициент линейной корреляции Пирсона (р-коэффициент). Первый метод вычисляется на основе ранжирования данных (упорядочивания), а второй метод основан на предварительном вычислении среднего значения и стандартного отклонения.

7. F-критерий Фишера - статистический критерий, используемый для выявления того, повлиял ли какой-то фактор на изменения измеряемых переменных. В случае когда стоит задача выявить влияние одного фактора проводится однофакторный дисперсионный анализ, для выявления влияния двух факторов на переменные, используется двухфакторный дисперсионный анализ.
1. Статистическая обработка данных.pptx