Statistical Approach to No C Design Itamar Cohen

Statistical Approach to No. C Design Itamar Cohen, Ori Rottenstreich and Isaac Keslassy Technion (Israel)

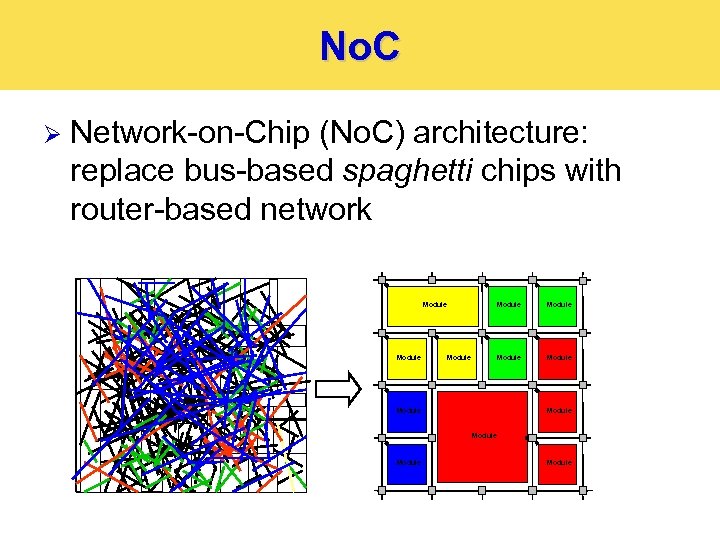No. C Ø Network-on-Chip (No. C) architecture: replace bus-based spaghetti chips with router-based network Module Network link Module Module Module Network router Computing module Bus

Problem The traffic matrix in No. Cs is often-changing and unpredictable makes No. Cs hard to design

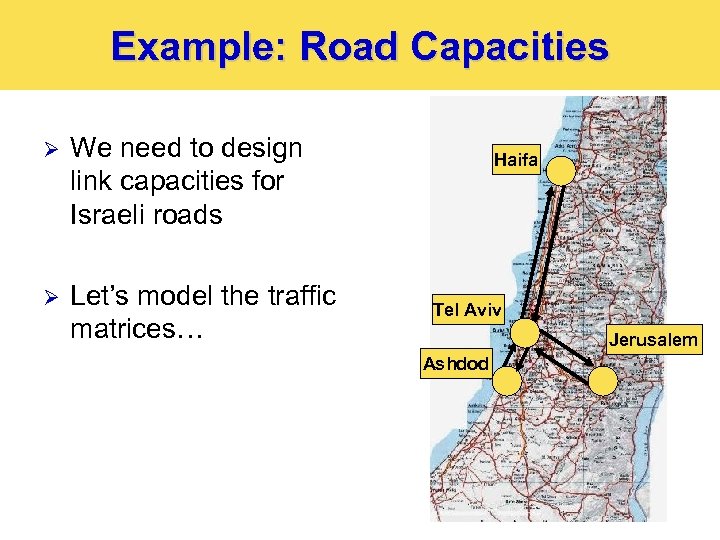Example: Road Capacities Ø We need to design link capacities for Israeli roads Ø Let’s model the traffic matrices… Haifa Tel Aviv Jerusalem Ashdod

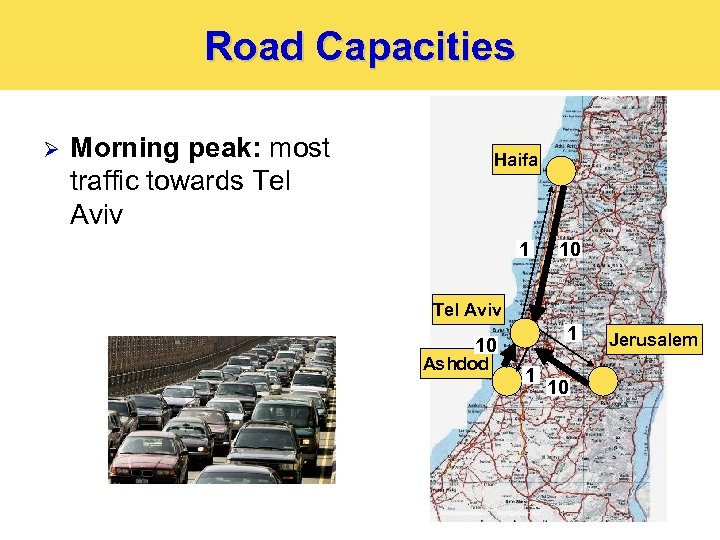Road Capacities Ø Morning peak: most traffic towards Tel Aviv Haifa 1 10 Tel Aviv 1 10 Ashdod 1 10 Jerusalem

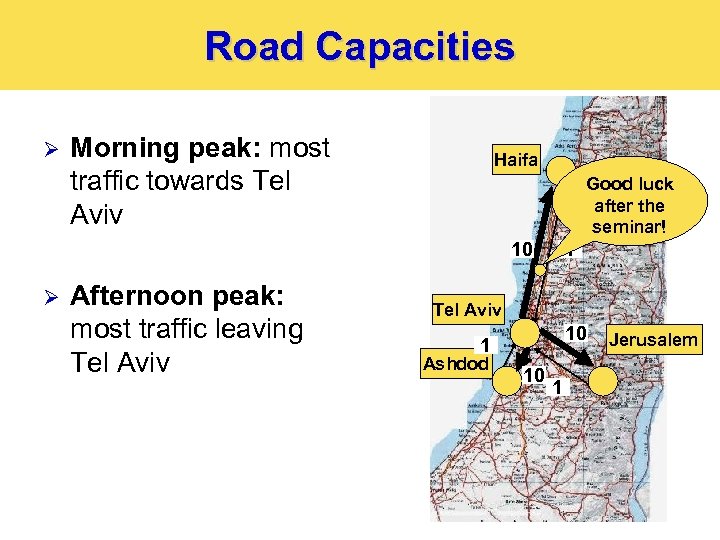Road Capacities Ø Morning peak: most traffic towards Tel Aviv Haifa Good luck after the seminar! 10 Ø Afternoon peak: most traffic leaving Tel Aviv 10 1 Ashdod 10 1 Jerusalem

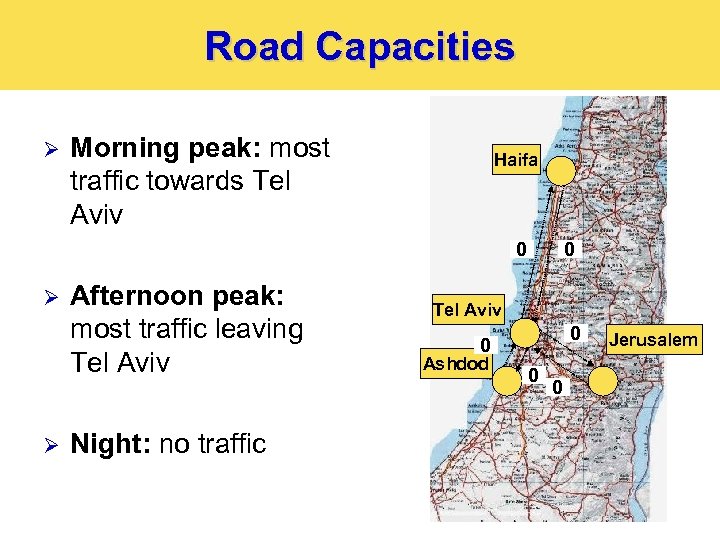Road Capacities Ø Morning peak: most traffic towards Tel Aviv Haifa 0 Ø Ø Afternoon peak: most traffic leaving Tel Aviv Night: no traffic 0 Tel Aviv 0 0 Ashdod 0 0 Jerusalem

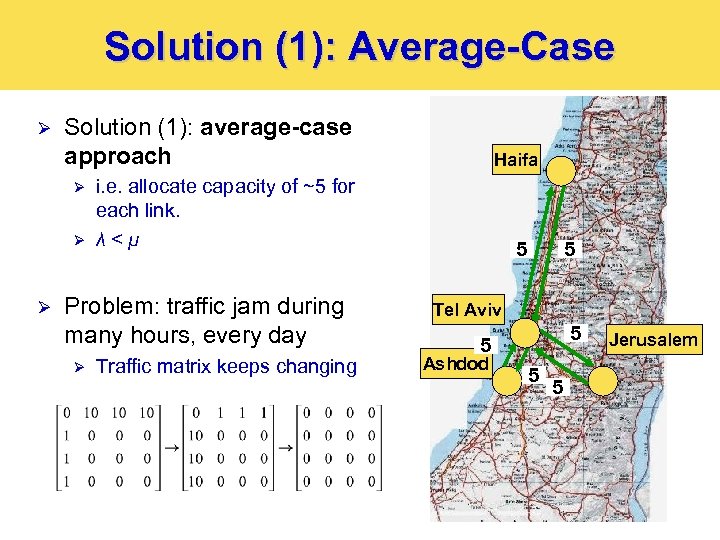Solution (1): Average-Case Ø Solution (1): average-case approach Ø Ø Ø i. e. allocate capacity of ~5 for each link. λ<μ Problem: traffic jam during many hours, every day Ø Haifa Traffic matrix keeps changing 5 5 Tel Aviv 5 5 Ashdod 5 5 Jerusalem

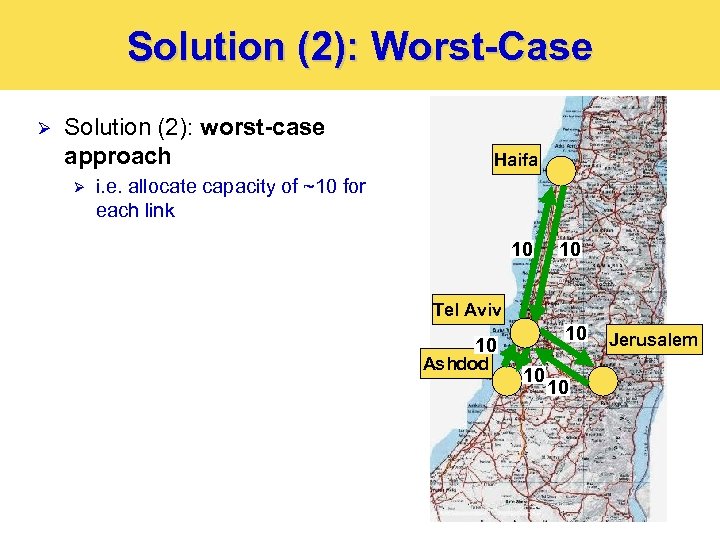Solution (2): Worst-Case Ø Solution (2): worst-case approach Ø Haifa i. e. allocate capacity of ~10 for each link 10 10 Tel Aviv 10 10 Ashdod 10 10 Jerusalem

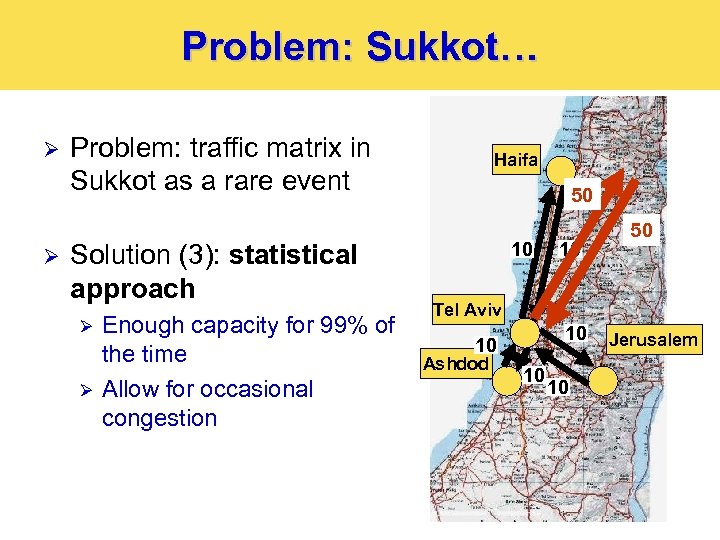Problem: Sukkot… Ø Ø Problem: traffic matrix in Sukkot as a rare event Solution (3): statistical approach Ø Ø Enough capacity for 99% of the time Allow for occasional congestion Haifa 50 10 10 50 Tel Aviv 10 10 Ashdod 10 10 Jerusalem

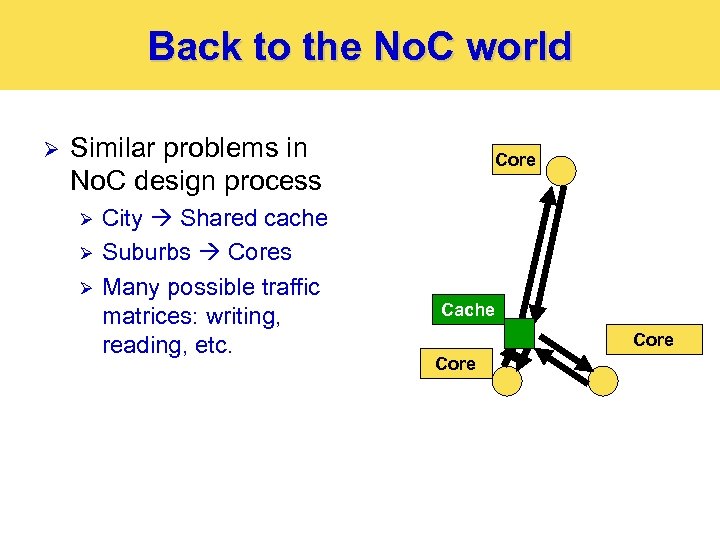Back to the No. C world Ø Similar problems in No. C design process Ø Ø Ø City Shared cache Suburbs Cores Many possible traffic matrices: writing, reading, etc. Core Cache Core

Statistical Approach to No. C Design Given: Ø Set of traffic matrices Ø Topology Ø Routing Ø Link capacities Compute congestion guarantee Ø “ 99% of traffic matrices will receive enough capacity”

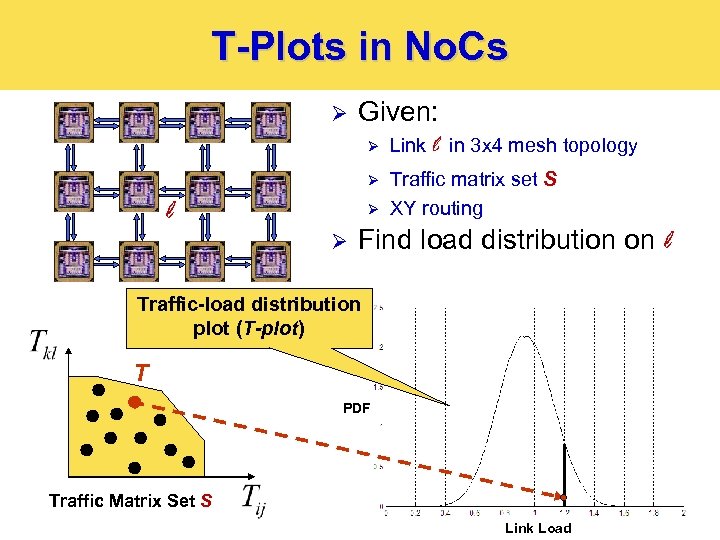T-Plots in No. Cs 2 2 Given: 2 2 1 1 1 2 2 Ø 1 1 1 l 2 1 2 2 Ø Link l in 3 x 4 mesh topology Ø 1 Traffic matrix set S XY routing 2 Ø 2 1 2 2 1 1 1 2 1 Ø Find load distribution on l 2 Traffic-load distribution plot (T-plot) T PDF Traffic Matrix Set S Link Load

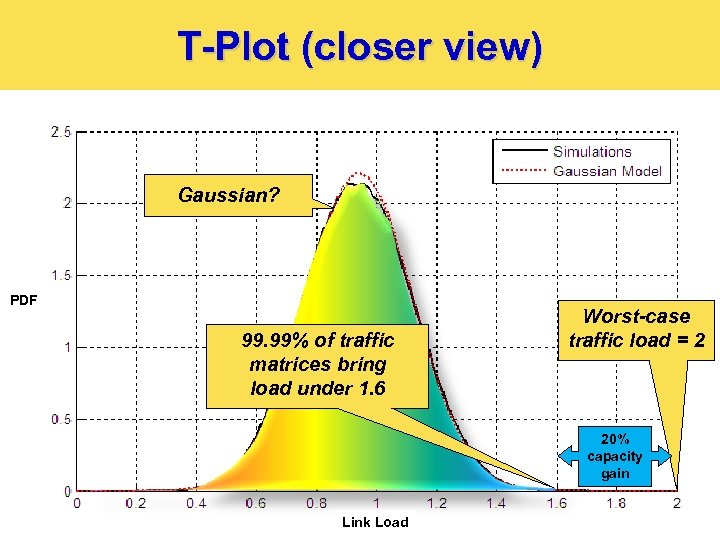T-Plot (closer view) Gaussian? PDF 99. 99% of traffic matrices bring load under 1. 6 Worst-case traffic load = 2 20% capacity gain 14 Link Load

Computing T-Plots Ø Theorem: for an arbitrary graph and routing, computing the T-Plot is #P-complete. Ø #P-complete problems are at least as hard as NPcomplete problems. Ø Ø NP: “Is there a solution? ” #P: “How many solutions? ”

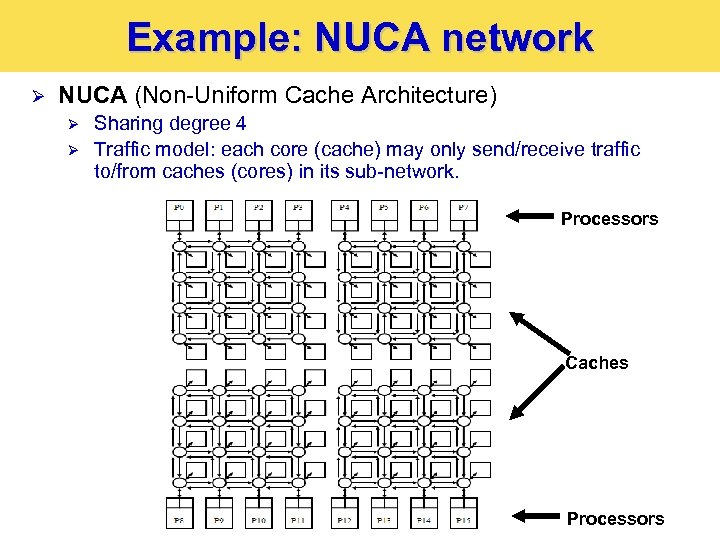Example: NUCA network Ø NUCA (Non-Uniform Cache Architecture) Ø Ø Sharing degree 4 Traffic model: each core (cache) may only send/receive traffic to/from caches (cores) in its sub-network. Processors Caches Processors

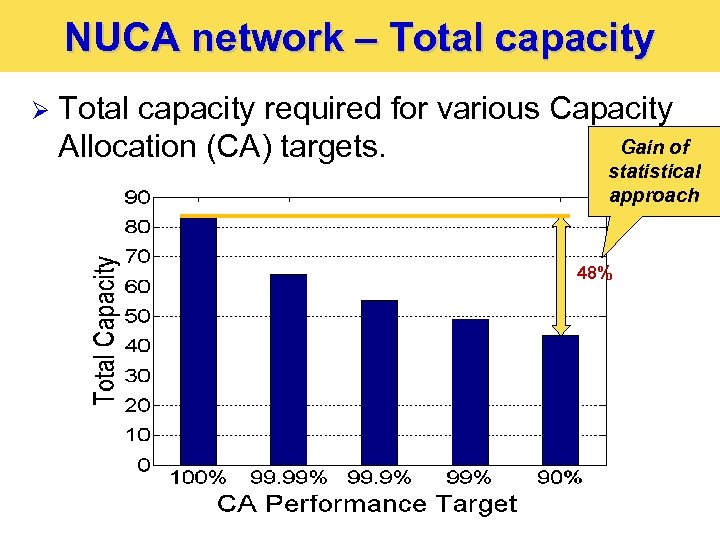NUCA network – Total capacity Ø Total capacity required for various Capacity Gain of Allocation (CA) targets. statistical approach 48%

Summary Ø Statistical approach Ø Deals with several traffic matrices Ø Can apply to nearly any network Ø Networks-on-Chip are a new and exciting field Ø Multi-core chips (Intel, AMD) Ø Technion No. C research group: www. ee. technion. ac. il/matrics

Thank you.