f05940e6485aae45b68c675d154f2f4b.ppt
- Количество слайдов: 67

Statistic Models for Web/Sponsored Search Click Log Analysis The Chinese University of Hong Kong Some slides are revised from Mr Guo Fan’s tutorial at CIKM 2009. 1
![Index • Background. • A Simple Click Model. – Dependent click model [WSDM 09]. Index • Background. • A Simple Click Model. – Dependent click model [WSDM 09].](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-2.jpg)
Index • Background. • A Simple Click Model. – Dependent click model [WSDM 09]. • Advanced Design. – Five extension directions. • Advanced Estimation. – Bayesian framework and the rationale. – Bayesian browsing model (BBM) [Liu 09]. – Click chain model (CCM) [Guo 09]. • Course Project. 2
Scenario: Web Search • Organic Results. • Sponsored Results. 3

User Click Log 36 1 23 2 18 3 4 5 11 36 • Which organic/sponsored result is more relevant to the query? • Is result 1 and result 5 equally relevant? 4

Eye-tracking User Study • Users have bias to examine the top results. 5
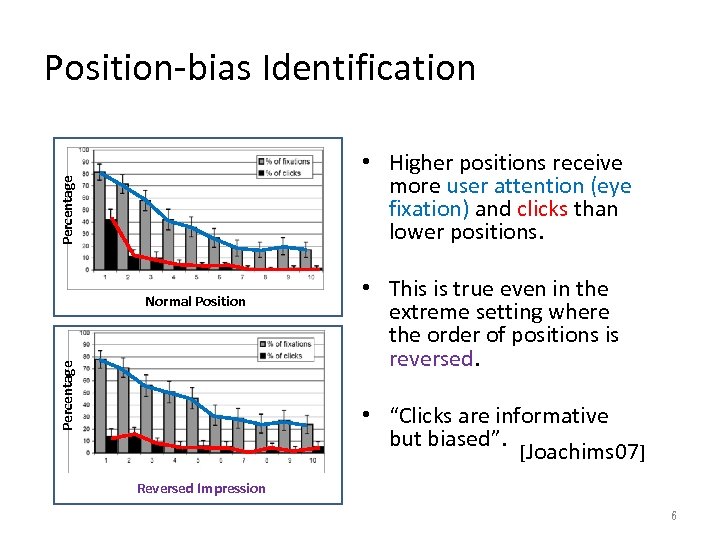
Position-bias Identification Percentage • Higher positions receive more user attention (eye fixation) and clicks than lower positions. Percentage Normal Position • This is true even in the extreme setting where the order of positions is reversed. • “Clicks are informative but biased”. [Joachims 07] Reversed Impression 6

Answer to Previous Example 36 1 23 2 18 3 4 5 11 36 • Result 5 is more relevant compared with Result 1. • Because Result 5 has less opportunity to be examined. 7

Click Model Motivation • Modeling the user’s click behavior in an interpreted manner and estimate the pure relevance of a query-document/ad pair regardless of bias. – Position-bias is the main problem. – Other kinds of bias. • • Influence among documents/ads Attractiveness bias Search intent bias … • Pure relevance of a query-document/ad pair intuition. – When the query is submitted to the search engine and only one single document/ad is shown, what is the click-through rate of this querydocument/ad pair? 8
![Examination Hypothesis [Richardson 07] • A document must be examined before a click. • Examination Hypothesis [Richardson 07] • A document must be examined before a click. •](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-9.jpg)
Examination Hypothesis [Richardson 07] • A document must be examined before a click. • The probability of click conditioned on being examined depends on the pure relevance of the query-document/ad pair. • The click probability could be decomposed. – Global component. • the examination probability which reflects the position-bias. – Local component (pure relevance). • click probability of the (query, URL) pair conditioned on being examined. 9

Click Models • Key tasks. – How to design the user examination behavior? – How to estimate the relevance of a query-doc/ad pair? • Desired Properties. – Effective: aware of the position-bias/other-bias and address it properly. – Scalable: linear complexity for both time and space, easy to parallel. – Incremental: flexible for model update based on new data. From this slide, “relevance” is equal to “pure relevance”. 10
Importance of Understanding Logs • Better matching query and documents/ads. • All the participants would benefit. – Users: better relevance. – Search engines: more revenue from advertisers and more users. – Advertisers: more return on investment (ROI). Advertiser Publisher User Better Match 11
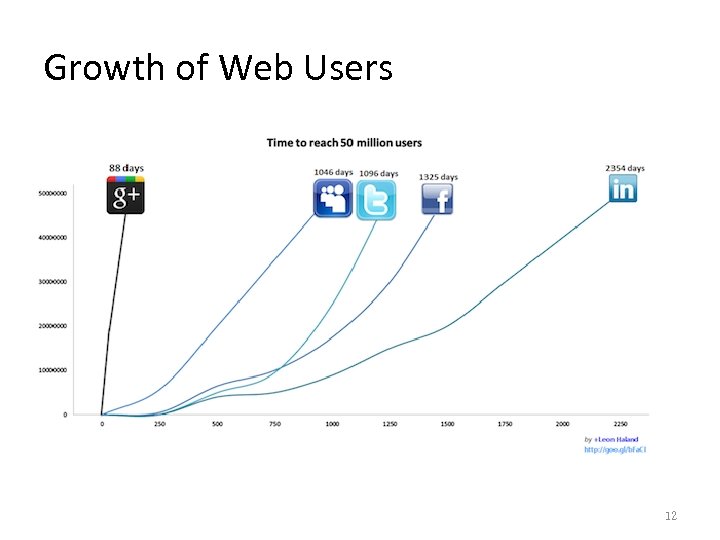
Growth of Web Users 12
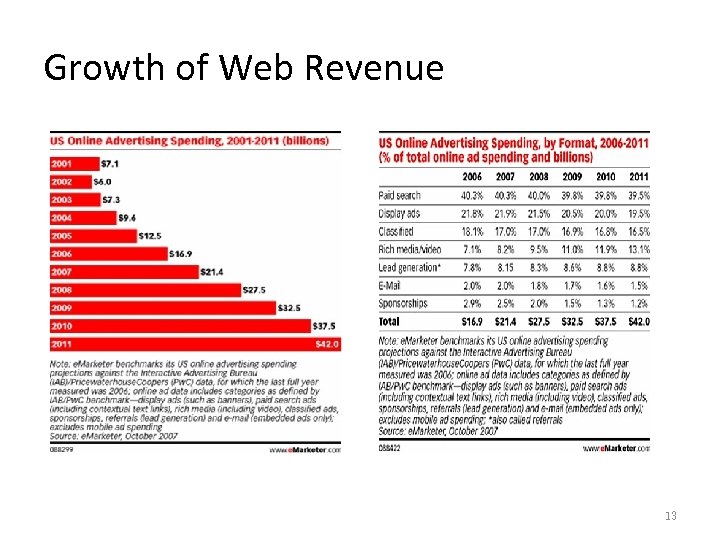
Growth of Web Revenue 13
![Index • Background. • A Simple Click Model. – Dependent Click Model [WSDM 09]. Index • Background. • A Simple Click Model. – Dependent Click Model [WSDM 09].](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-14.jpg)
Index • Background. • A Simple Click Model. – Dependent Click Model [WSDM 09]. • Advanced Design. • Advanced Estimation. • Projects. 14

Notations – Ei • binary r. v. for Examination Event on position i; – Ci • binary r. v. for Click Event on position i; – ri = p(Ci = 1| Ei = 1) • relevance for the query-document pair on position i. 15
![Click Model Design Dependent Click Model (DCM) [GUO 09] 16 Click Model Design Dependent Click Model (DCM) [GUO 09] 16](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-16.jpg)
Click Model Design Dependent Click Model (DCM) [GUO 09] 16

Parameters in DCM • r=p(C=1|E=1) is local parameter. – Modeling the relevance of a query-document/ad pair. – The position-bias has been modeled by p(E=1). • λ is global parameter. – Modeling p(Ei+1=1|Ci=1, Ei=1). Parameters estimation Maximum log-likelihood method 17

Estimation of r: Step 1 • Define as last click position. • When there is no click, is the last position. cikm Query Pos URL Click 1 2 3 4 5 6 cikm 2008. org www. cikm. org www. fc. ul. pt/cikmconf. org www. cikm. com/. . . Ir. iit. edu/cikm 2004 0 1 0 cikm Query Pos URL Click 1 2 3 4 5 6 cikm 2008. org www. cikm. org www. fc. ul. pt/cikmconf. org www. cikm. com/. . . Ir. iit. edu/cikm 2004 0 0 0 18
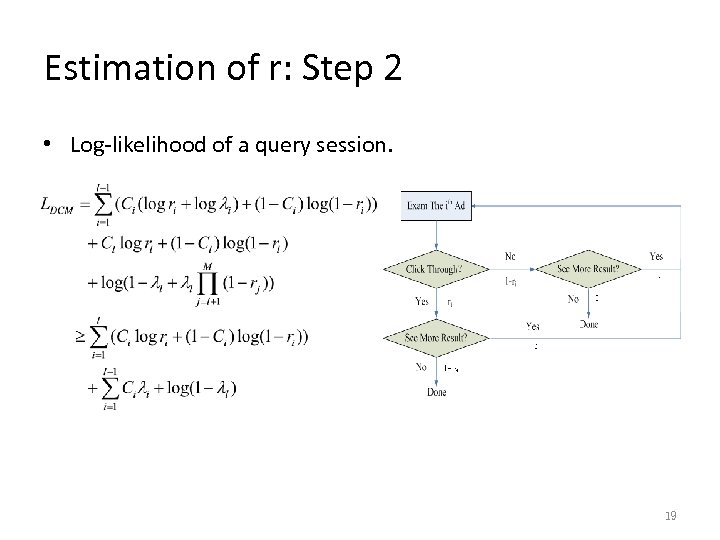
Estimation of r: Step 2 • Log-likelihood of a query session. 19

Estimation of r: Step 3 • By maximizing the lower bound of the log-likelihood, we have Suppose the current pair has occurred in different sessions. For M sessions, it occurs before/on l and has been clicked; for N sessions, it occurs before/on l and is not clicked. 20

Estimation of λ • For a specific , By maximizing the lower bound of the loglikelihood, we have Suppose there are totally A sessions. In B sessions, the position l is large than position i and click event happens in position i. In C sessions, the position l is just equal to position i. Other cases happen in the other A-B-C sessions. 21
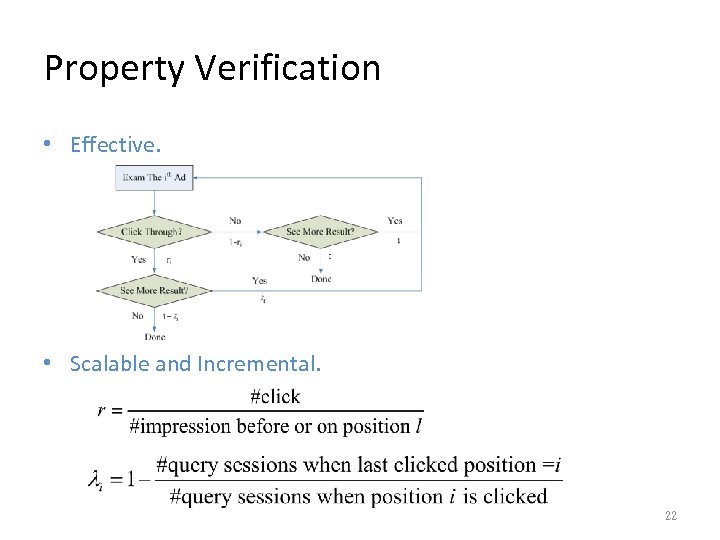
Property Verification • Effective. • Scalable and Incremental. 22

Evaluation Criteria for DCM • Log-likelihood. – Given the document impression in the test set. – Compute the chance to recover the entire click vector. – Averaged over different query sessions. 23
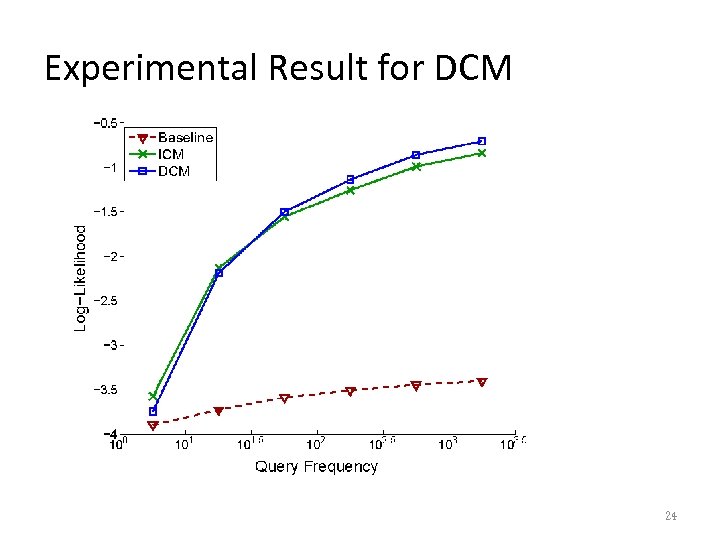
Experimental Result for DCM 24

Some Other Evaluations • Log-likelihood. – http: //en. wikipedia. org/wiki/Likelihood_function#Log-likelihood • Perplexity. – http: //en. wikipedia. org/wiki/Perplexity • Root mean square error (RMSE). – http: //en. wikipedia. org/wiki/Root-mean-square_deviation • Area under ROC curve. – http: //en. wikipedia. org/wiki/Receiver_operating_characteristic 25

Index • Background. • A Simple Click Model. • Advanced Design. – Five extension directions. • Advanced Estimation. • Project. 26
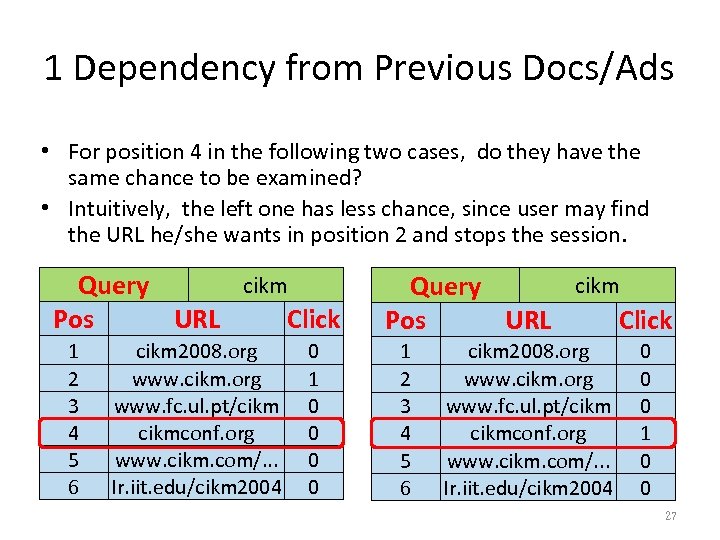
1 Dependency from Previous Docs/Ads • For position 4 in the following two cases, do they have the same chance to be examined? • Intuitively, the left one has less chance, since user may find the URL he/she wants in position 2 and stops the session. cikm Query Pos URL Click 1 2 3 4 5 6 cikm 2008. org www. cikm. org www. fc. ul. pt/cikmconf. org www. cikm. com/. . . Ir. iit. edu/cikm 2004 0 1 0 0 cikm Query Pos URL Click 1 2 3 4 5 6 cikm 2008. org www. cikm. org www. fc. ul. pt/cikmconf. org www. cikm. com/. . . Ir. iit. edu/cikm 2004 0 0 0 1 0 0 27
![Solution: Click Chain Model [Guo 09] • The chance of being examined depend on Solution: Click Chain Model [Guo 09] • The chance of being examined depend on](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-28.jpg)
Solution: Click Chain Model [Guo 09] • The chance of being examined depend on the relevance of previous documents/ads. • Other similar work includes [Dupret 08][Liu 09]. 28
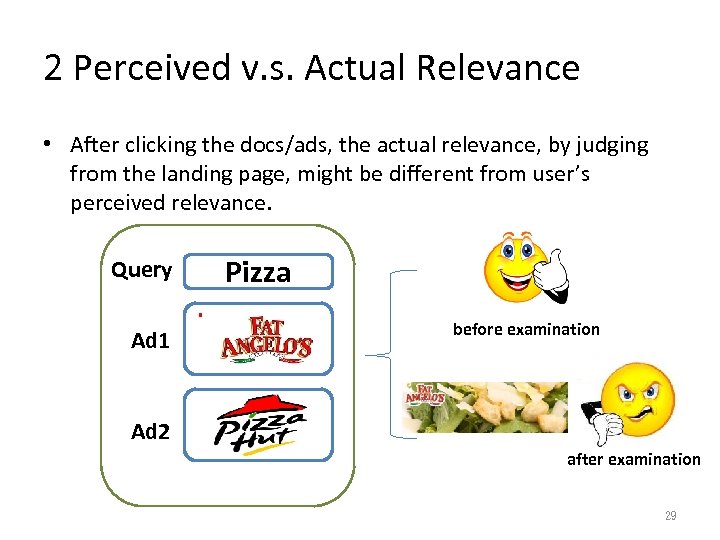
2 Perceived v. s. Actual Relevance • After clicking the docs/ads, the actual relevance, by judging from the landing page, might be different from user’s perceived relevance. Query Ad 1 Pizza before examination Ad 2 after examination 29
![Solution: Dynamic Bayesian Network [Chapelle 09] • For each ad, two kinds of relevance Solution: Dynamic Bayesian Network [Chapelle 09] • For each ad, two kinds of relevance](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-30.jpg)
Solution: Dynamic Bayesian Network [Chapelle 09] • For each ad, two kinds of relevance are defined, perceived relevance r and actual relevance s. s would influence the examination probability of the latter docs/ads. 30
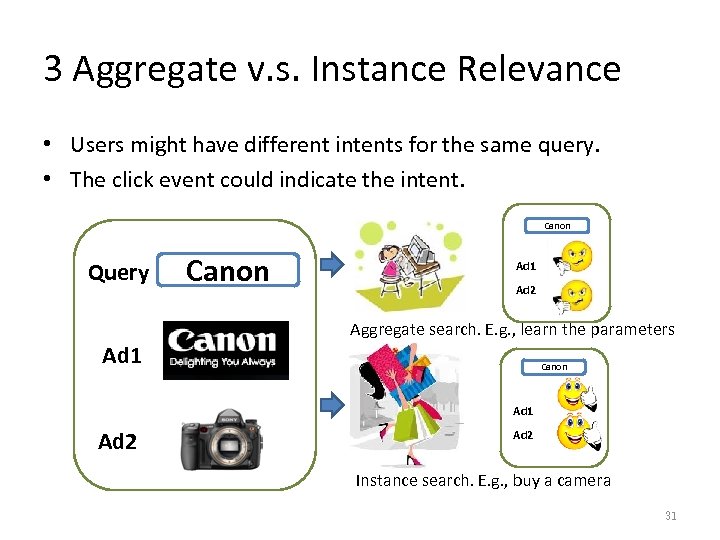
3 Aggregate v. s. Instance Relevance • Users might have different intents for the same query. • The click event could indicate the intent. Canon Query Canon Ad 1 Ad 2 Aggregate search. E. g. , learn the parameters Ad 1 Canon Ad 1 Ad 2 Instance search. E. g. , buy a camera 31
![Solution: Joint Relevance Examination Model [Srikant 10] • Add a correction factor , which Solution: Joint Relevance Examination Model [Srikant 10] • Add a correction factor , which](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-32.jpg)
Solution: Joint Relevance Examination Model [Srikant 10] • Add a correction factor , which is determined by the click events of other docs/ads. • Other similar work includes [Hu 11]. 32
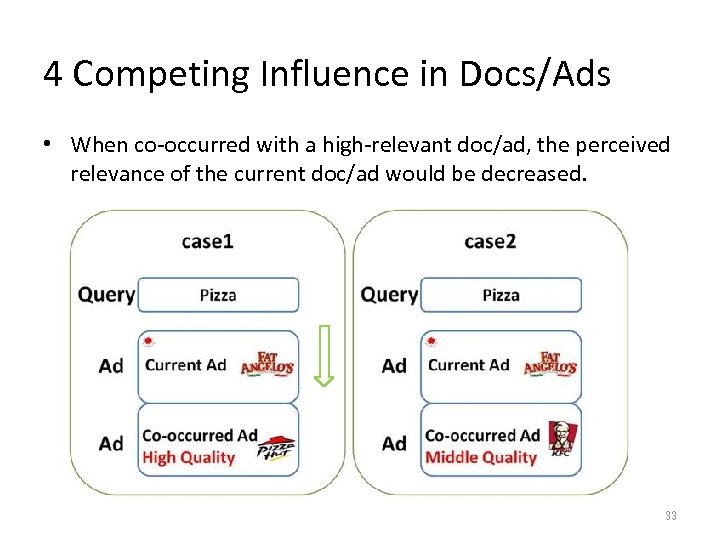
4 Competing Influence in Docs/Ads • When co-occurred with a high-relevant doc/ad, the perceived relevance of the current doc/ad would be decreased. 33
![Solution: Temporal Click Model [Xu 10] • The docs/ads are competed to win the Solution: Temporal Click Model [Xu 10] • The docs/ads are competed to win the](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-34.jpg)
Solution: Temporal Click Model [Xu 10] • The docs/ads are competed to win the priority to be examined. 34
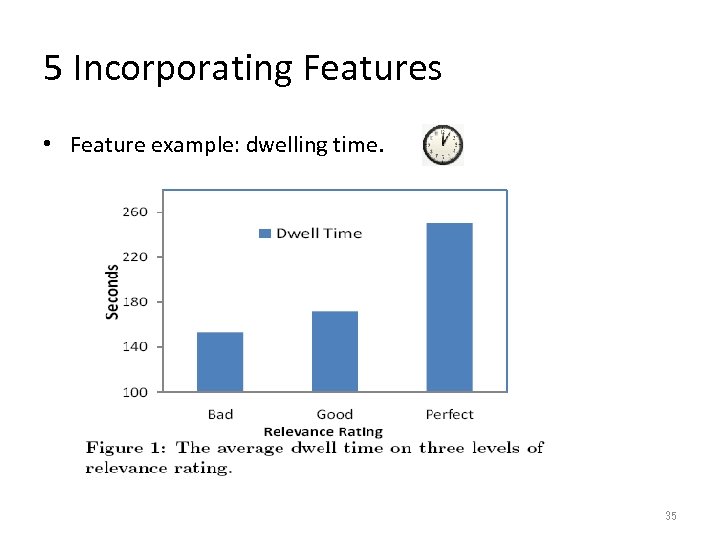
5 Incorporating Features • Feature example: dwelling time. 35
![Solution: Post-Clicked Click Model [Zhong 10] • Incorporating features to determine the relevance. • Solution: Post-Clicked Click Model [Zhong 10] • Incorporating features to determine the relevance. •](https://present5.com/presentation/f05940e6485aae45b68c675d154f2f4b/image-36.jpg)
Solution: Post-Clicked Click Model [Zhong 10] • Incorporating features to determine the relevance. • Other similar work include [Zhu 10]. 36

Index • • Background. A Simple Click Model. Advanced Design. Advanced Estimation. – Bayesian framework and the rationale. – Bayesian browsing model. – Click chain model. • Project. 37

Limitation of Maximum Log-likelihood • Cannot fit the scalable and incremental properties. – It has difficulty in getting closed-formula, when the model is complex. – Even in DCM as shown in this page, we need to approximate a lower bound for easy calculation. • No prior information could be utilized in such sparse data environment. Log-likelihood of DCM 38

An Coin-Toss Example for Bayesian Framework • Scenario: to estimate the probability of tossing a head according to the following five training samples. • The probability is a variable X = x. • Each training sample is denoted by Ci , e. g. , C 1 = 1, C 4=0. • According to Bayesian rule, we have 39
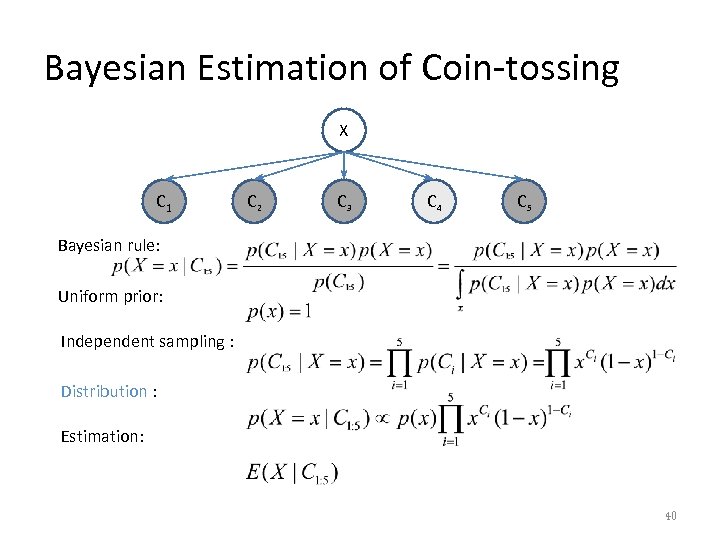
Bayesian Estimation of Coin-tossing X C 1 C 2 C 3 C 4 C 5 Bayesian rule: Uniform prior: Independent sampling : Distribution : Estimation: 40

Density Function Update of Cointossing Posterior Prior Density Function (not normalized) x 1(1 -x)0 x 2(1 -x)0 x 3(1 -x)1 x 4(1 -x)1 41
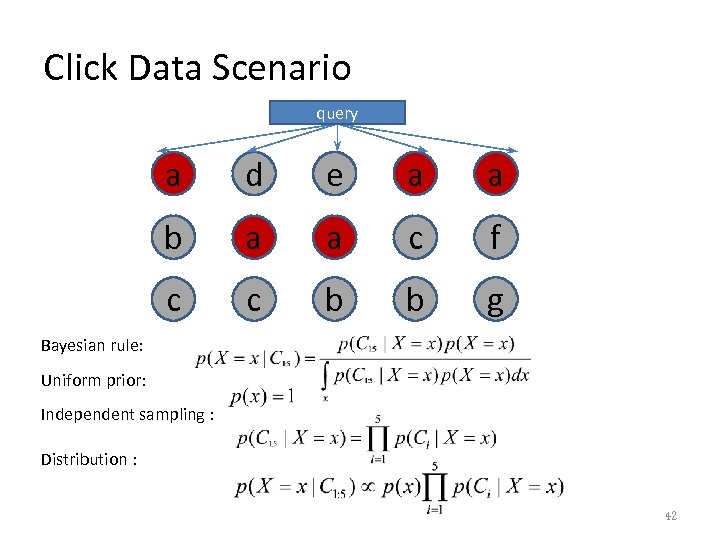
Click Data Scenario query a d e a a b a a c f c c b b g Bayesian rule: Uniform prior: Independent sampling : Distribution : 42

Factor Trick Distribution : • If the factors of p(C|X) are arbitrary, for each training sample, a unique factor of p(X) must be stored. Thus it is space consuming; • However if the factors of p(C|X) are from a small discrete set, only the exponents are needed to be stored. 43
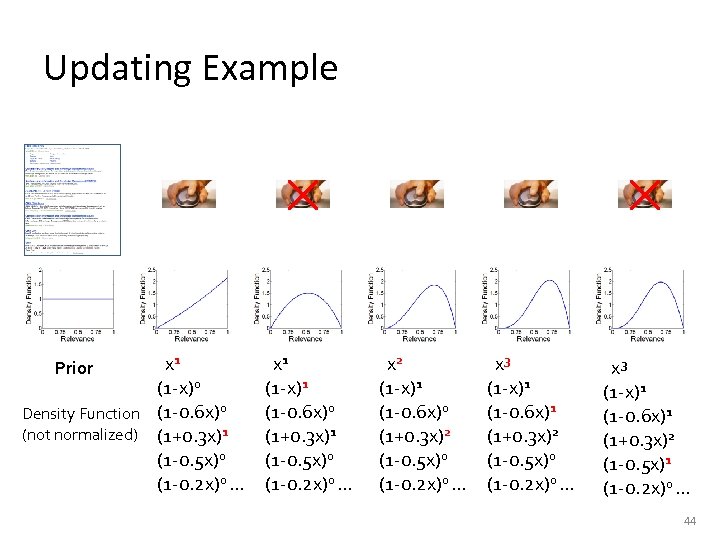
Updating Example x 1 (1 -x)0 Density Function (1 -0. 6 x)0 (not normalized) (1+0. 3 x)1 (1 -0. 5 x)0 (1 -0. 2 x)0 … Prior x 1 (1 -x)1 (1 -0. 6 x)0 (1+0. 3 x)1 (1 -0. 5 x)0 (1 -0. 2 x)0 … x 2 (1 -x)1 (1 -0. 6 x)0 (1+0. 3 x)2 (1 -0. 5 x)0 (1 -0. 2 x)0 … x 3 (1 -x)1 (1 -0. 6 x)1 (1+0. 3 x)2 (1 -0. 5 x)1 (1 -0. 2 x)0 … 44

How to realize the factor trick? • Setting a global parameter for all cases. – Bayesian browsing model (BBM) [Liu 09]. • Assuming all other docs/ads follows the same distribution and integrating them. – Click chain model (CCM) [Guo 09]. In the following two example, we only concern the estimation of r using Bayesian framework. The estimation of other parameters are all based on maximizing the log -likelihood similarly as shown in DCM. Please refer the original paper for details. 45

Index • • Background. A Simple Click Model. Advanced Design. Advanced Estimation. – Bayesian framework and the rationale. – Bayesian browsing model. – Click chain model. • Project. 46

BBM Variable Definition • For a specific query session, let – ri, the relevance variable at position i. – Ei, the binary examination variable at position i. – Ci, the binary click variable at position i. – ni, last click position before position i. – di, the distance between position i and its previous clicked position. 47

Small Discrete Set of Beta • Suppose M = 3 for simplicity illustration. • There are only 6 values of beta. n=0 d=1 n=0 d=2 n=0 d=3 n=1 d=1 n=1 d=2 n=2 d=1 48

Estimation Algorithms How many times the Doc/ad was clicked How many times the Doc/ad was not clicked with the probability of betan, d 49

Toy Example Step 1 • Only top M=3 positions are shown, 3 query sessions and 4 distinct URLs. Position 1 2 3 Query Session 1 1 2 3 Query Session 2 1 3 4 Query Session 3 1 3 4 50

Toy Example Step 2 • Initialize M(M+1)/2+1 counts for each URL Clicks n=0 d=1 n=0 d=2 n=0 d=3 n=1 d=1 n=1 d=2 n=2 d=1 4 0 0 0 0 51

Toy Example Step 3 • Update counts for URL 4. – If not impressed, do nothing; – If clicked, increment “clicks” by 1; – Otherwise, locate the right r and d to increment. URL Clicks n=0 d=1 n=0 d=2 n=0 d=3 n=1 d=1 n=1 d=2 n=2 d=1 4 0 0 0 0 52

Toy Example Step 4 • Update counts for URL 4. – If not impressed, do nothing; – If clicked, increment “clicks” by 1; – Otherwise, locate the right r and d to increment. URL Clicks n=0 d=1 n=0 d=2 n=0 d=3 n=1 d=1 n=1 d=2 n=2 d=1 4 0 0 0 1 53

Toy Example Step 5 • Update counts for URL 4. – If not impressed, do nothing; – If clicked, increment “clicks” by 1; – Otherwise, locate the right r and d to increment. URL Clicks n=0 d=1 n=0 d=2 n=0 d=3 n=1 d=1 n=1 d=2 n=2 d=1 4 1 0 0 0 1 54

Toy Example Step 6 • The posterior for URL 4. URL Clicks n=0 d=1 n=0 d=2 n=0 d=3 n=1 d=1 n=1 d=2 n=2 d=1 4 1 0 0 0 1 • Interpretation: – The larger the probability of examination, the stronger the penalty for a non-click. 55

Algorithm Complexities • Let • Initializing and updating the counts: – Time: Space: Linear to the size of the click log Almost constant storage required 56

Index • • Background. A Simple Click Model. Advanced Design. Advanced Estimation. – Bayesian framework and the rationale. – Bayesian browsing model. – Click chain model. • Project. 57
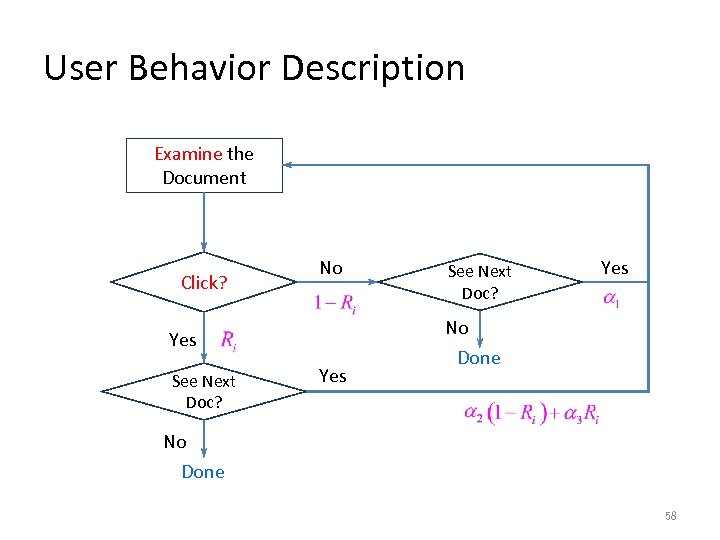
User Behavior Description Examine the Document Click? No Yes See Next Doc? Yes No Done 58

Estimation Algorithms • By assuming other docs/ads in a session follow the same distribution and integrate them, the factors f p(C|R) could be described from a small discrete set. 59

Five Cases • The current doc/ad may occur in five different cases. • For each case, there would be unique factors for p(C|Ri). 60
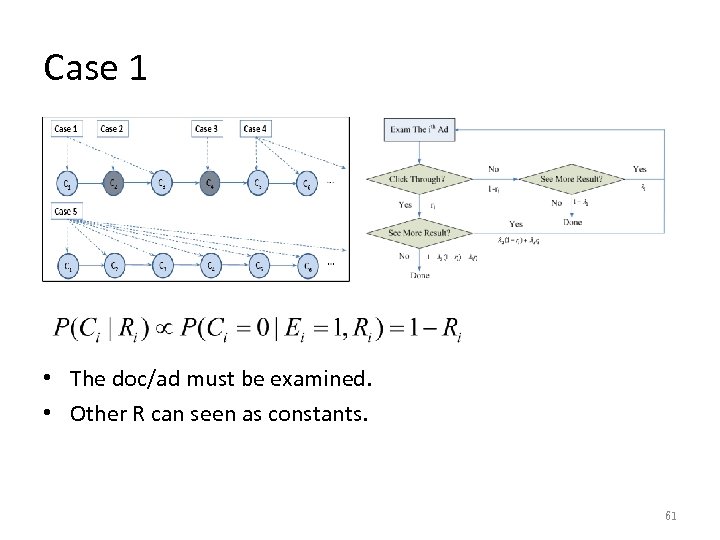
Case 1 • The doc/ad must be examined. • Other R can seen as constants. 61
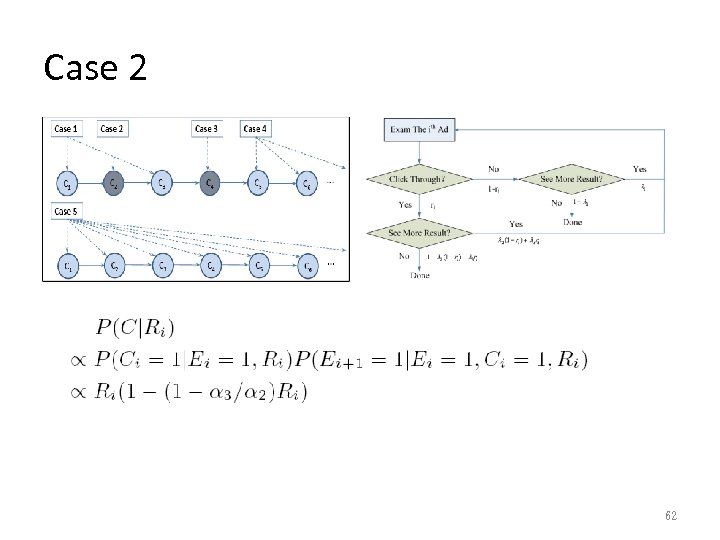
Case 2 62
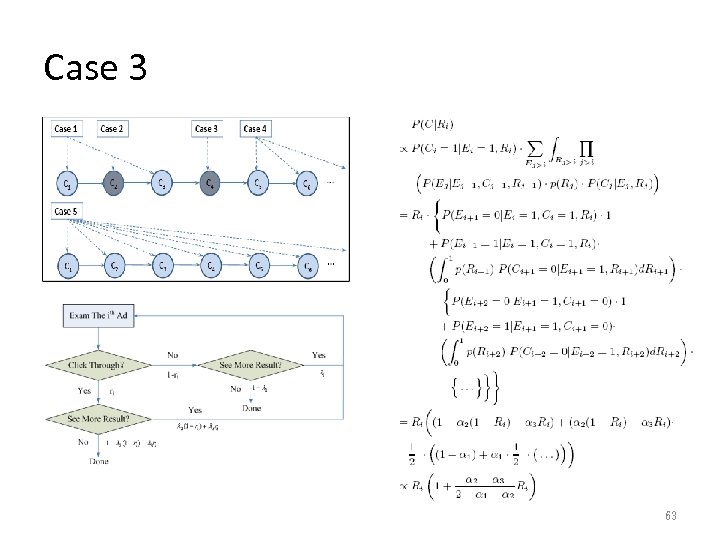
Case 3 63

All Cases • By assuming other docs/ads in a session follows the same distribution and integrate them, the factors f p(C|R) could be described from a small discrete set. 64

Index • • • Background. A Simple Click Model. Advanced Design. Advanced Estimation. Project. 65

Description • Fake dataset. • Format. – – query. Id ad 1 Id, click ad 2 Id, click ad 3 Id, click • Evaluation Metric: ROC. • Baseline. – Average (Avg). • Current competitive method. – Simplified CCM (SCCM). • Task. – Implement another advanced click model. – Compare the result with the Avg and SCCM. – Analyzing the reasons of improvement. 66

End 67
f05940e6485aae45b68c675d154f2f4b.ppt