СТАТИКА ЛЕКЦИЯ 4 ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ 1

СТАТИКА ЛЕКЦИЯ 4: ПРОСТРАНСТВЕННАЯ СИСТЕМА СИЛ

1. СТАТИЧЕСКИЕ ИНВАРИАНТЫ По теореме Пуансо любая система сил приведении к произвольно выбранному центру О заменяется одной силой FО и одной парой с моментом МО При изменении центра приведения Главный вектор остается без изменения: он представляет собой инвариант системы по отношению к изменению центра. Cкалярное произведение тоже инвариант Первый статический инвариант Второй статический инвариант , узком смысле

2. ДИНАМО Если то проекция главного момента на направление главного вектора не меняется Для центра приведения , где модуль главного момента минимален. В этом случае Система силы и пары с моментом коллинеарном силе называется динамой или динамическим винтом Правый винт Левый винт

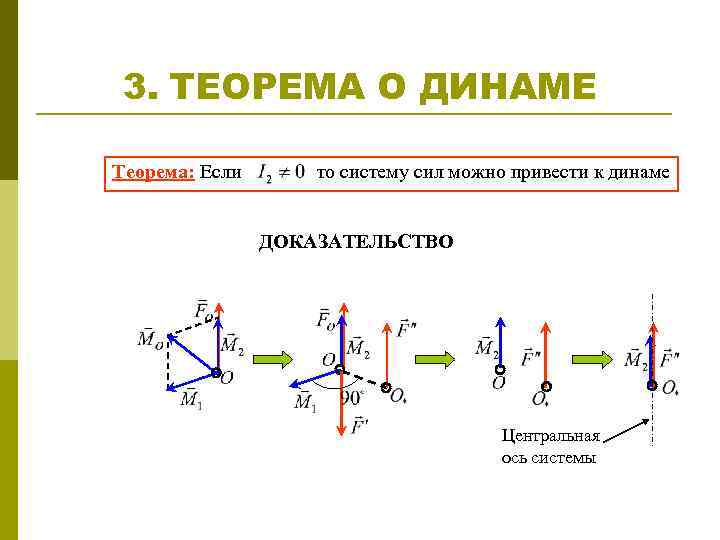3. ТЕОРЕМА О ДИНАМЕ Теорема: Если то систему сил можно привести к динаме ДОКАЗАТЕЛЬСТВО Центральная ось системы

4. УРАВНЕНИЕ ЦЕНТРАЛЬНОЙ ОСИ Известны Найти центральную ось системы

5. РАВНОДЕЙСТВУЮЩАЯ, ТЕОРЕМА ВАРИНЬОНА Система приводится к равнодействующей тогда и только тогда когда Необходимость очевидна. Достаточность Теорема Вариньона. Если система сил имеет равнодействующую, то момент этой равнодействующей относительно произвольного центра равен сумме моментов всех сил системы относительно того же центра. Пусть О лежит на линии действия равнодействующей, О 1 – любая другая точка ч. т. д.

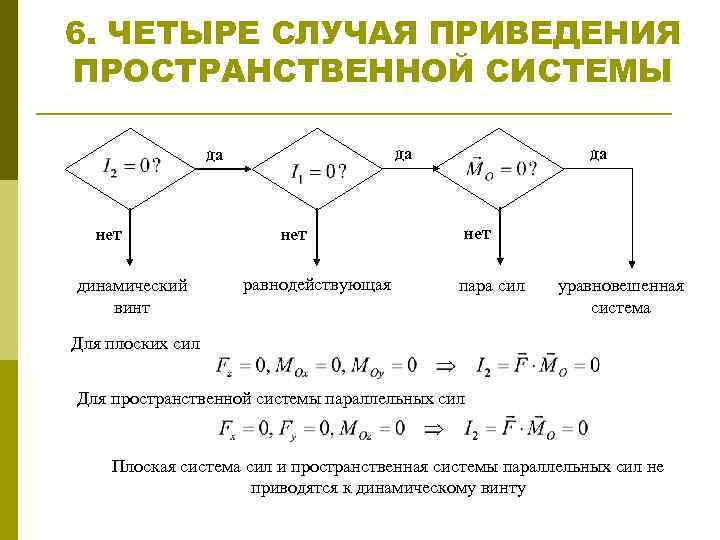6. ЧЕТЫРЕ СЛУЧАЯ ПРИВЕДЕНИЯ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ нет динамический винт да да да нет равнодействующая нет пара сил уравновешенная система Для плоских сил Для пространственной системы параллельных сил Плоская система сил и пространственная системы параллельных сил не приводятся к динамическому винту

7. УРАВНЕНИЯ РАВНОВЕСИЯ ПРОСТРАНСТВЕННОЙ СИСТЕМЫ В векторной форме два необходимых и достаточных условия равновесия произвольной системы сил имеют вид В проекциях на оси координат число условий равновесия для пространственной системы сил будет равно шести Если тело полностью закреплено, то эти условия служат для определения опорных реакций. Для пространственной системы параллельных сил условия равновесия принимают вид

8. УРАВНЕНИЯ РАВНОВЕСИЯ ТЕЛА С 1 -й НЕПОДВИЖНОЙ ТОЧКОЙ Тело прикреплено к неподвижной точке А сферическим шарниром. Служат для определения реакций Устанавливают зависимости между активными силами, необходимые для равновесия тела Условием равновесия тела с неподвижной точкой является равенство нулю сумм моментов активных сил относительно неподвижной токи

9. УРАВНЕНИЯ РАВНОВЕСИЯ ТЕЛА С 2 -мя НЕПОДВИЖНЫМИ ТОЧКАМИ Тело прикреплено к неподвижным точкам А и В сферическими шарнирами. Устанавливает зависимости между активными силами, необходимые для равновесия тела Условием равновесия тела с 2 -мя неподвижными точками является равенство нулю сумм моментов активных сил относительно оси, проходящей через неподвижные точки

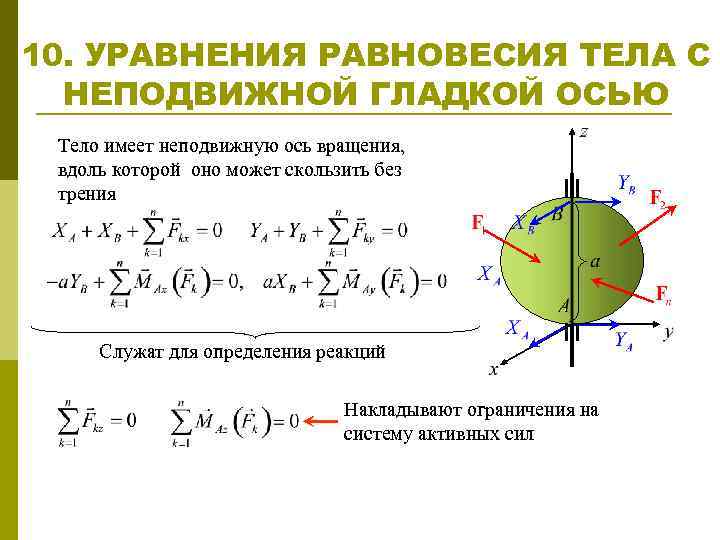10. УРАВНЕНИЯ РАВНОВЕСИЯ ТЕЛА С НЕПОДВИЖНОЙ ГЛАДКОЙ ОСЬЮ Тело имеет неподвижную ось вращения, вдоль которой оно может скользить без трения Служат для определения реакций Накладывают ограничения на систему активных сил