СТАТИКА ЛЕКЦИЯ 1 ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ

СТАТИКА ЛЕКЦИЯ 1: ОСНОВНЫЕ ПОНЯТИЯ И ИСХОДНЫЕ ПОЛОЖЕНИЯ СТАТИКИ

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА ПО КУРСУ СТАТИКИ • • М. И. БАТЬ, Г. Ю. ДЖАНЕЛИДЗЕ, А. С. КЕЛЬЗОН ТЕОРЕТИЧЕСКАЯ МЕХАНИКА В ПРИМЕРАХ И ЗАДАЧАХ ТОМ ПЕРВЫЙ : СТАТИКА И КИНЕМАТИКА С. М. ТАРГ КРАТКИЙ КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ Н. Н. БУХГОЛЬЦ ОСНОВНОЙ КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ ЧАСТЬ ПЕРВАЯ: КИНЕМАТИКА, СТАТИКА, ДИНАМИКА МАТЕРИАЛЬНОЙ ТОЧКИ Н. В. БУТЕНИН, Я. Л. ЛУНЦ, Д. Р. МЕРКИН КУРС ТЕОРЕТИЧЕСКОЙ МЕХАНИКИ ТОМ ПЕРВЫЙ : СТАТИКА И КИНЕМАТИКА

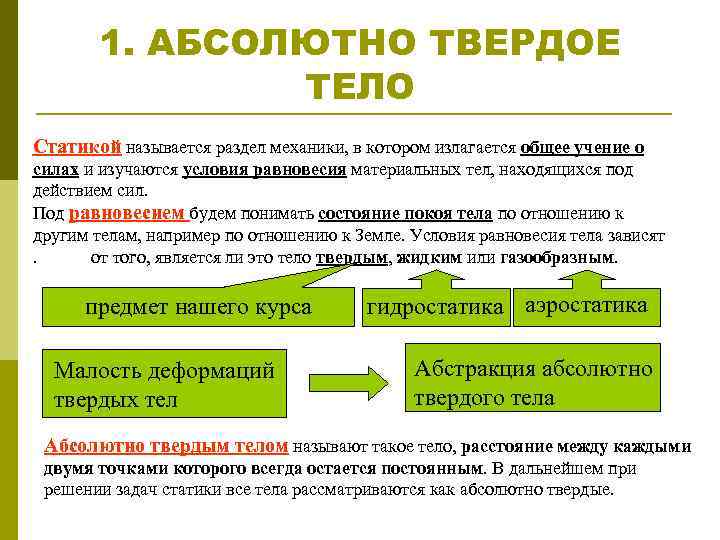1. АБСОЛЮТНО ТВЕРДОЕ ТЕЛО Статикой называется раздел механики, в котором излагается общее учение о силах и изучаются условия равновесия материальных тел, находящихся под действием сил. Под равновесием будем понимать состояние покоя тела по отношению к другим телам, например по отношению к Земле. Условия равновесия тела зависят. от того, является ли это тело твердым, жидким или газообразным. предмет нашего курса Малость деформаций твердых тел гидростатика аэростатика Абстракция абсолютно твердого тела Абсолютно твердым телом называют такое тело, расстояние между каждыми двумя точками которого всегда остается постоянным. В дальнейшем при решении задач статики все тела рассматриваются как абсолютно твердые.

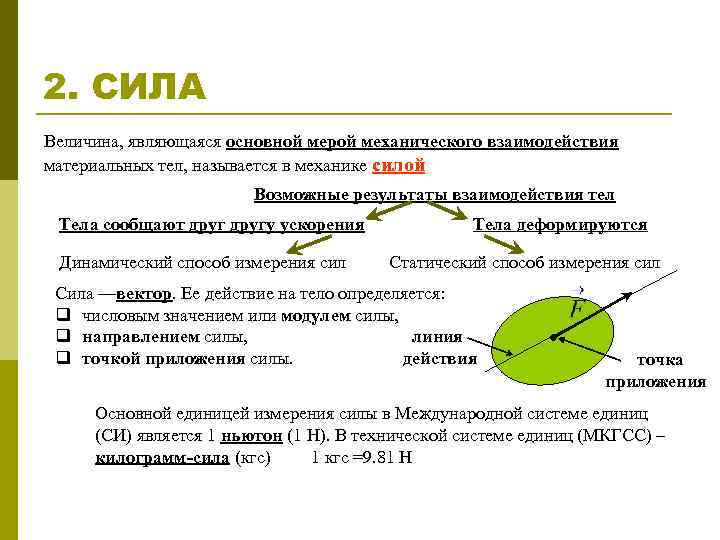2. СИЛА Величина, являющаяся основной мерой механического взаимодействия материальных тел, называется в механике силой Возможные результаты взаимодействия тел Тела сообщают другу ускорения Динамический способ измерения сил Тела деформируются Статический способ измерения сил Сила —вектор. Ее действие на тело определяется: q числовым значением или модулем силы, линия q направлением силы, действия q точкой приложения силы. точка приложения Основной единицей измерения силы в Международной системе единиц (СИ) является 1 ньютон (1 Н). В технической системе единиц (МКГСС) – килограмм-сила (кгс) 1 кгс =9. 81 Н

3. ОПРЕДЕЛЕНИЯ 1)Система сил = совокупность сил, действующих на рассматриваемое тело. 2) Если линии действия всех сил лежат в одной плоскости система сил – плоская 3) Если линии действия не лежат в одной плоскости— пространственная 4) Силы, линии действия которых пересекаются в одной точке —сходящиеся. 5) Силы, линии действия которых параллельны другу, — параллельные. 6) Если не изменяя состояния тела, одну систему сил, (F 1, F 2, …, Fn) можно заменить другой системой, (G 1, G 2, …, Gk), то такие две системы сил называются эквивалентными (F 1, F 2, …, Fn) (G 1, G 2, …, Gk). Замечания • Не изменяя состояния тела означает не изменяя скоростей точек тела • Понятия эквивалентности сил и равенства изображающих их векторов различны. В математике два вектора равны если они параллельны, направлены в одну сторону и равны по модулю. Такие вектора в механике называются свободными. В определении силы однако участвует еще и точка приложения!

4. ОПРЕДЕЛЕНИЯ 7) Если (F 1, F 2, …, Fn) G то G - равнодействующая Замечание: Не всякая система сил имеет равнодействующую 8) Система сил, под действием которой твердое тело может находиться в покое, называется уравновешенной или эквивалентной нулю. (F 1, F 2, …, Fn) 0 Замечание: Почему нулю? Потому что твердое тело находиться в покое когда на него не действуют никакие силы (1 -й закон Ньютона) 9) Силы, действующие на тело (или систему тел), разделяют на внешние и внутренние. Внешние - силы, которые действуют на это тело (или на тела системы) со стороны других тел, а внутренние — силы, с которыми части данного тела (или тела данной системы) действуют друг на друга.

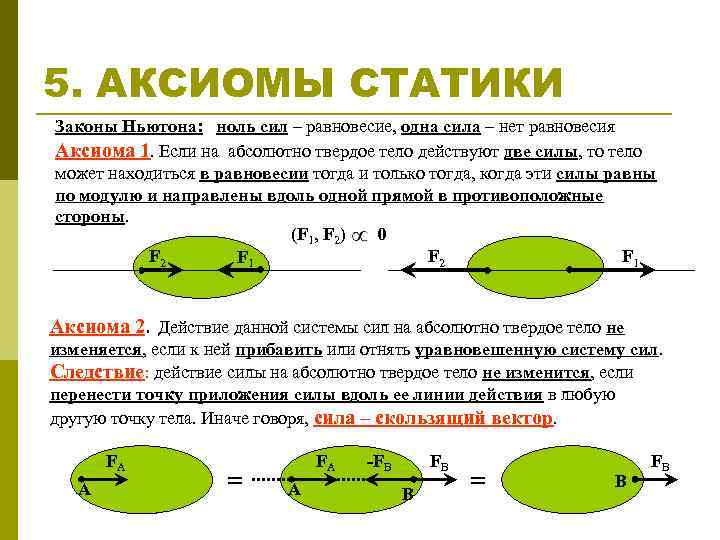5. АКСИОМЫ СТАТИКИ Законы Ньютона: ноль сил – равновесие, одна сила – нет равновесия Аксиома 1. Если на абсолютно твердое тело действуют две силы, то тело может находиться в равновесии тогда и только тогда, когда эти силы равны по модулю и направлены вдоль одной прямой в противоположные стороны. (F 1, F 2) 0 F 2 F 1 Аксиома 2. Действие данной системы сил на абсолютно твердое тело не изменяется, если к ней прибавить или отнять уравновешенную систему сил. Следствие: действие силы на абсолютно твердое тело не изменится, если перенести точку приложения силы вдоль ее линии действия в любую другую точку тела. Иначе говоря, сила – скользящий вектор. FA A = FA A -FB FB B = B FB

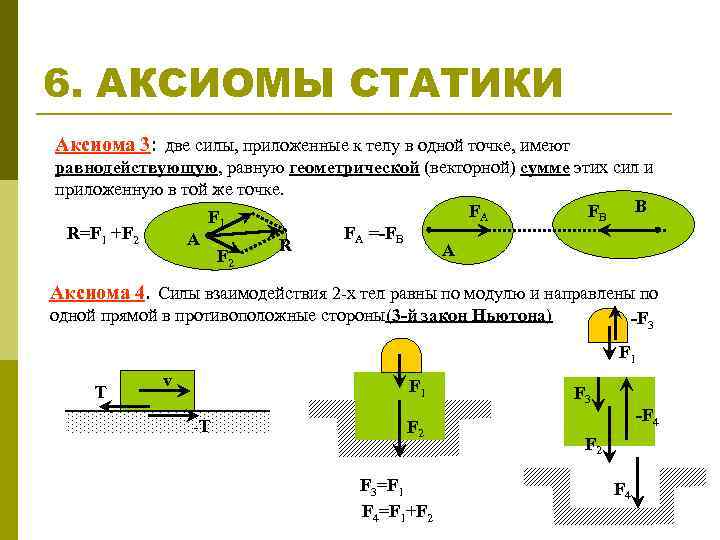6. АКСИОМЫ СТАТИКИ Аксиома 3: две силы, приложенные к телу в одной точке, имеют равнодействующую, равную геометрической (векторной) сумме этих сил и приложенную в той же точке. B FA FB F 1 FA =-FB R=F 1 +F 2 A R A F 2 Аксиома 4. Силы взаимодействия 2 -х тел равны по модулю и направлены по одной прямой в противоположные стороны(3 -й закон Ньютона) -F 3 F 1 T v F 1 -T F 2 F 3=F 1 F 4=F 1+F 2 F 3 -F 4 F 2 F 4

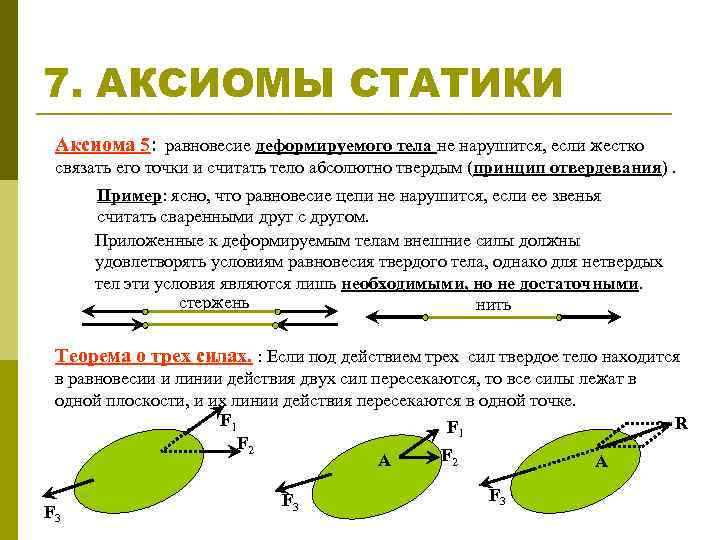7. АКСИОМЫ СТАТИКИ Аксиома 5: равновесие деформируемого тела не нарушится, если жестко связать его точки и считать тело абсолютно твердым (принцип отвердевания). Пример: ясно, что равновесие цепи не нарушится, если ее звенья считать сваренными друг с другом. Приложенные к деформируемым телам внешние силы должны удовлетворять условиям равновесия твердого тела, однако для нетвердых тел эти условия являются лишь необходимыми, но не достаточными. стержень нить Теорема о трех силах. : Если под действием трех сил твердое тело находится в равновесии и линии действия двух сил пересекаются, то все силы лежат в одной плоскости, и их линии действия пересекаются в одной точке. F 1 F 2 A A F 3 F 3 R

8. СВЯЗИ И ИХ РЕАКЦИИ По определению, тело, которое может совершать из данного положения любые перемещения в пространство, называется свободным. Тело, перемещениям которого в пространстве препятствуют какие-нибудь другие, скрепленные или соприкасающиеся с ним, тела, называется несвободным. Все то, что ограничивает перемещения данного тела в пространстве, называют связью. Сила, с которой данная связь действует на тело, препятствуя тем или иным его перемещениям, называется силой реакции связи или просто реакцией связи. Принцип освобождаемости: несвободное тело можно рассматривать как свободное, если действие связей заменить их реакциями, приложенными к данному телу. Все силы при этом оказываются разбиты на две группы : активные (не зависящие от связей) и пассивные (реакции связей) Значение реакции связи зависит от других действующих сил и наперед неизвестно; для ее определения надо решить соответствующую задачу механики. Направлена реакция связи в сторону, противоположную той, куда связь не дает перемещаться телу. Когда связь может препятствовать перемещениям тела по нескольким направлениям, направление реакции такой связи тоже наперед неизвестно и должно определяться в результате решения

9. ВИДЫ СВЯЗЕЙ: гладкая поверхность или опора Гладкой будем называть поверхность, трением о которую данного тела можно в первом приближении пренебречь. Такая поверхность не дает телу перемещаться только по направлению общего перпендикуляра (нормали) к поверхностям соприкасающихся тел в точке их касания. Поэтому реакция N гладкой поверхности или опоры направлена по общей нормали к поверхностям соприкасающихся тел в точке их касания и приложена в этой точке. N N 2 N N 1 Ny N Nx

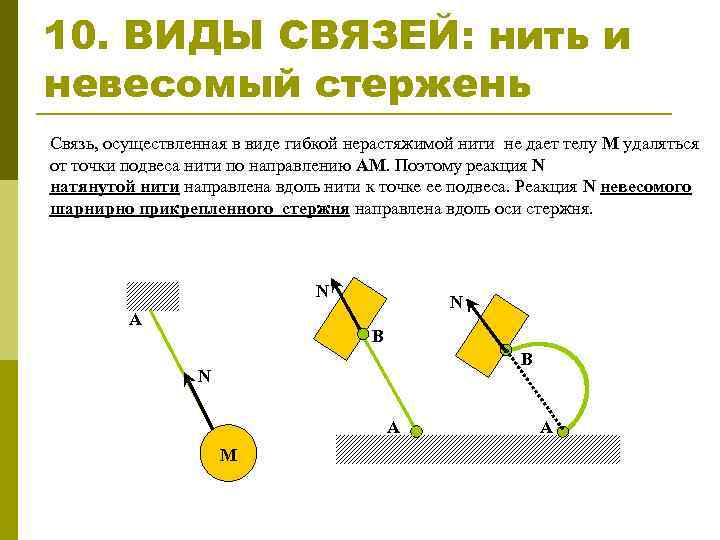10. ВИДЫ СВЯЗЕЙ: нить и невесомый стержень Связь, осуществленная в виде гибкой нерастяжимой нити не дает телу М удаляться от точки подвеса нити по направлению AM. Поэтому реакция N натянутой нити направлена вдоль нити к точке ее подвеса. Реакция N невесомого шарнирно прикрепленного стержня направлена вдоль оси стержня. N A N B B N A M A

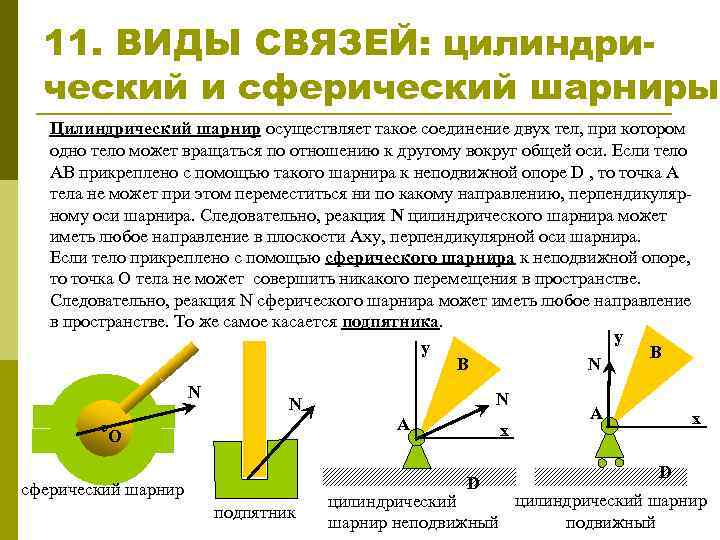11. ВИДЫ СВЯЗЕЙ: цилиндрический и сферический шарниры Цилиндрический шарнир осуществляет такое соединение двух тел, при котором одно тело может вращаться по отношению к другому вокруг общей оси. Если тело АB прикреплено с помощью такого шарнира к неподвижной опоре D , то точка А тела не может при этом переместиться ни по какому направлению, перпендикулярному оси шарнира. Следовательно, реакция N цилиндрического шарнира может иметь любое направление в плоскости Аху, перпендикулярной оси шарнира. Если тело прикреплено с помощью сферического шарнира к неподвижной опоре, то точка O тела не может совершить никакого перемещения в пространстве. Следовательно, реакция N сферического шарнира может иметь любое направление в пространстве. То же самое касается подпятника. y y B B N N A O x D сферический шарнир подпятник A x D цилиндрический шарнир цилиндрический подвижный шарнир неподвижный

12. ОСНОВНЫЕ ЗАДАЧИ СТАТИКИ Задача о приведении системы сил: как данную систему сил заменить другой, в частности наиболее простой, ей эквивалентной? Задача о равновесии: каким условиям должна удовлетворять система сил, приложенная к данному телу, чтобы она была уравновешенной системой? Первая задача имеет важное значение не только в статике, но и в динамике Вторая задача ставится когда известно, что тело находится в равновесии, которое обеспечивается связями, наложенными на тело. При этом условия равновесия устанавливают зависимость между всеми силами, приложенными к телу; это, в частности, позволяет определить опорные реакции. Последние необходимы для последующего расчета прочности конструкции

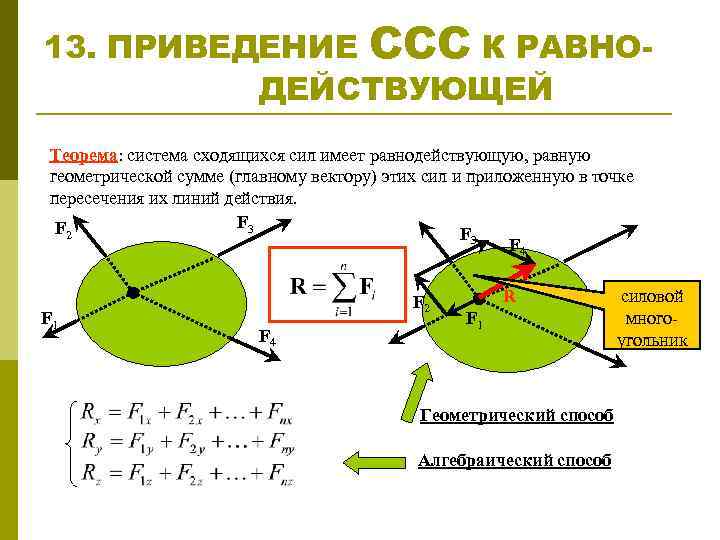13. ПРИВЕДЕНИЕ ССС К РАВНОДЕЙСТВУЮЩЕЙ Теорема: система сходящихся сил имеет равнодействующую, равную геометрической сумме (главному вектору) этих сил и приложенную в точке пересечения их линий действия. F 3 F 2 F 3 F 4 F 1 F 2 F 4 R F 1 Геометрический способ Алгебраический способ силовой многоугольник

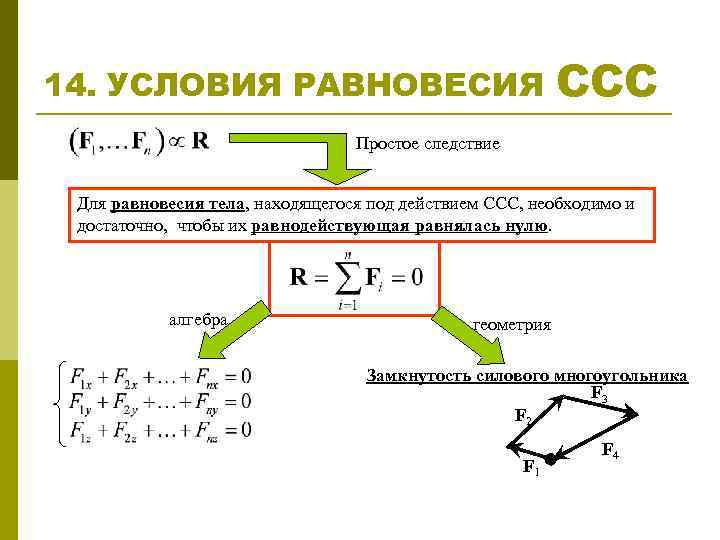14. УСЛОВИЯ РАВНОВЕСИЯ ССС Простое следствие Для равновесия тела, находящегося под действием ССС, необходимо и достаточно, чтобы их равнодействующая равнялась нулю. алгебра геометрия Замкнутость силового многоугольника F 3 F 2 F 1 F 4

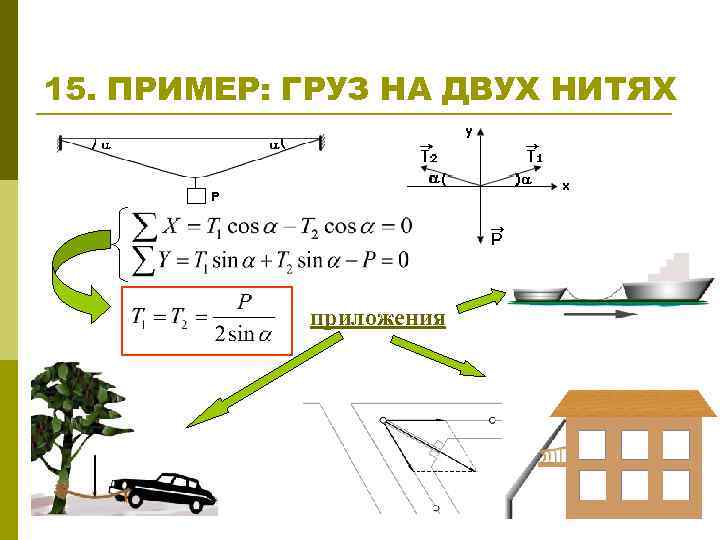15. ПРИМЕР: ГРУЗ НА ДВУХ НИТЯХ приложения

16. ПРИМЕР: ПРОСТЕЙШАЯ СТЕРЖНЕВАЯ КОНСТРУКЦИЯ Стержень AO растянут, BO – сжат. Оптимальный вариант: при каком конструкция имеет наименьший вес? Чтобы выдержать нагрузку стержень должен иметь площадь поперечного сечения не меньше, чем , где - постоянная материала.