Статические структуры данных Векторы Вектор одномерный массив

Статические структуры данных

Векторы Вектор (одномерный массив) - структура данных с фиксированным числом элементов одного и того же типа. Каждый элемент вектора имеет уникальный в рамках заданного вектора номер. Обращение к элементу вектора выполняется по имени вектора и номеру требуемого элемента.

var m 1: array[-2. . 2] of real;

Количество байтов непрерывной области памяти, занятых одновременно вектором Byte. Sise = ( k - n + 1 ) * Sizeof (тип) Обращение к i-тому элементу вектора выполняется по адресу вектора плюс смещение к данному элементу. Смещение i-ого элемента вектора определяется по формуле: Byte. Numer = ( i- n ) * Sizeof (тип), а адрес его: @ Byte. Number = @ имя + Byte. Number где @ имя - адрес первого элемента вектора.

var МAS: array [ 5. . 10 ] of word Смещение +0 (байт) +2 +4 +6 +8 + 10 Идентифик MAS[5] атор поля MAS[6] MAS[7] MAS[8] MAS[9] MAS[10]

вектор будет занимать в памяти: (10 -5+1)*2 = 12 байт. Смещение к элементу вектора с номером 8: (8 -5)*2 = 6 Адрес элемента с номером 8: @ MAS + 6 адрес i-го элемента может быть вычислен: @Имя[i] = @Имя + i*Sizeof(тип) - n*Sizeof(тип) на этапе выполнения, должны быть известны параметры: @Имя Sizeof(тип), n, при каждом обращении должны выполняться две операции умножения и две - сложения. @Имя[i] = A 0 + i*Sizeof(тип) A 0 = @Имя - n*Sizeof(тип)

Дескриптор сократить время доступа обеспечивает проверку правильности обращения -обращения к дескриптору - это команды -память как для размещения самого дескриптора, так и команд, с ним работающих.

C Дескриптор вектора отсутствует (не сохраняется на этапе выполнения) Индексация массивов в C обязательно начинается с нуля Компилятор каждое обращение к элементу массива заменяет на последовательность команд, реализующую частный случай формулы при n = 0: @Имя[i] = @Имя + i*Sizeof(тип) Имя[i] = *(Имя+i).

Массивы Массив - структура данных, которая характеризуется: фиксированным набором элементов одного и того же типа; каждый элемент имеет уникальный набор значений индексов; количество индексов определяют мерность массива, например, два индекса - двумерный массив, три индекса трехмерный массив, один индекс - одномерный массив или вектор; обращение к элементу массива выполняется по имени массива и значениям индексов для данного элемента. Другое определение: массив - это вектор, каждый элемент которого - вектор.

< Имя > : Array [n 1. . k 1] [n 2. . k 2]. . [nn. . kn] of < Тип > Mas 2 D : Array [n 1. . k 1] [n 2. . k 2] of < Тип > Mas 2 D : Array [n 1. . k 1 , n 2. . k 2] of < Тип >

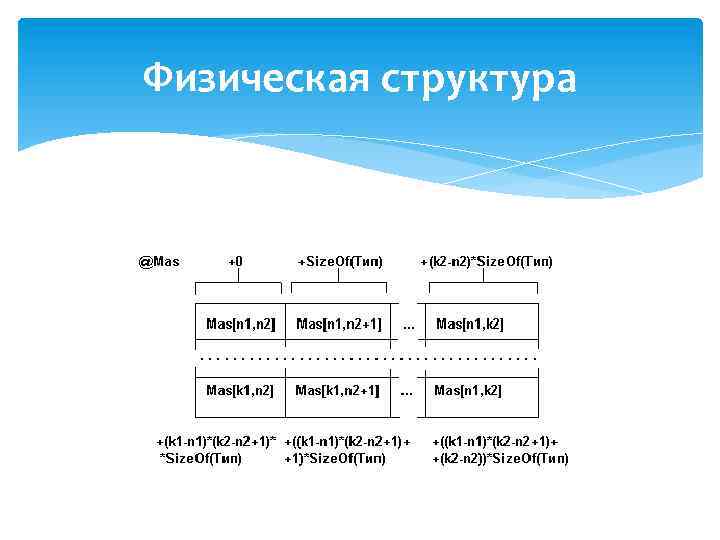
Физическая структура

Количество байтов : Byte. Size = (k 1 -n 1+1)*(k 2 -n 2+1)*Size. Of(Тип) Адресом массива является адрес первого байта начального компонента массива. Смещение к элементу массива Mas[i 1, i 2] определяется по формуле: Byte. Number = [(i 1 -n 1)*(k 2 -n 2+1)+(i 2 -n 2)]*Size. Of(Тип) адрес : @Byte. Number = @mas + Byte. Number.

A[i] , i: integer A[i], i: string _root[“a”+i].

var Mas : Array [3. . 5] [7. . 8] of Word; @Mas+((4 -3)*(8 -7+1)+(8 -7)*2 = @Mas+6 Смещение (байт) Идентификатор поля +0 Mas[3, 7] +2 Mas[3, 8] +4 Mas[4, 7] +6 Mas[4, 8] +8 Mas[5, 7] + 10 Mas[5, 8]

Addr[I(1), I(2)] = Addr[B(1), B(2)] + { [I(1)-B(1)] * [E(2)-B(2)+1] + [I(2)-B(2)] }*Size. Of(Тип) Mas[B(1). . E(2)][B(2). . E(2)]. . . [B(n). . E(n)] Addr[I(1), I(2), . . . , I(n)] = Addr[B(1), B(2), . . . B(n)] Sizeof(Тип)*СУММА[B(m)*D(m)] + Sizeof(Тип)*СУММА[I(m)*D(m)] где Dm зависит от способа размещения массива. При размещении по строкам: D(m)=[E(m+1)-B(m+1)+1]*D(m+1), где m = n-1, . . . , 1 и D(n)=1 при размещении по столбцам: D(m)=[E(m-1)-B(m-1)+1]*D(m-1), где m = 2, . . . , n и D(1)=1

1 4 5 4 2 6 5 6 3

D(m) также могут быть вычислены заранее и сохраняться в дескрипторе массива начальный адрес массива - Addr[I(1), I(2), . . . , I(n)]; число измерений в массиве - n; постоянную составляющую формулы линеаризации для каждого из n измерений массива: значения граничных индексов - B(i), E(i); множитель формулы линеаризации - D(i).

PL/1 DECLARE A(10, 10) BINARY FIXED; A[*, I] - будет обращаться к одномерному массиву, состоящему из элементов: A(1, I), A(2, I), . . . , A(10, I).

Адресация элементов с помощью векторов Айлиффа

Симметричные массивы количество строк равно количеству столбцов называется квадратной матрицей. Квадратная матрица, у которой элементы, расположенные симметрично относительно главной диагонали, попарно равны другу, называется симметричной. Если матрица порядка n симметрична, то в ее физической структуре достаточно отобразить не n^2, а лишь n*(n+1)/2 элементов

преобразования индексов матрицы в индекс вектора, формирования вектора и записи в него элементов верхнего треугольника элементов исходной матрицы, получения значения элемента матрицы из ее упакованного представления. При таком подходе обращение к элементам исходной матрицы выполняется опосредованно, через указанные функции.

Разреженные массивы массив, большинство элементов которого равны между собой, так что хранить в памяти достаточно лишь небольшое число значений отличных от основного (фонового) значения остальных элементов. два типа разреженных массивов: 1) массивы, в которых местоположения элементов со значениями отличными от фонового, могут быть математически описаны; 2) массивы со случайным расположением элементов.

Массивы с математическим описанием местоположения нефоновых элементов массивы, у которых местоположения элементов со значениями отличными от фонового, могут быть математически описаны, т. е. в их расположении есть какаялибо закономерность. Элементы, значения которых являются фоновыми, называют нулевыми; элементы, значения которых отличны от фонового, - ненулевыми. Ненулевые значения хранятся, как правило, в одномерном массиве, а связь между местоположением в исходном, разреженном, массиве и в новом, одномерном, описывается математически с помощью формулы, преобразующей индексы массива в индексы вектора. На практике для работы с разреженным массивом разрабатываются функции: для преобразования индексов массива в индекс вектора; для получения значения элемента массива из ее упакованного представления по двум индексам (строка, столбец); для записи значения элемента массива в ее упакованное представление по двум индексам.

2 2 2

Пример Unit Compr. Matr; Interface Function Put. Tab(y, x, value : integer) : boolean; Function Get. Tab(x, y: integer) : integer; Implementation Const XM=. . . ; Var arrp: array[1. . XM*XM div 2] of integer; Function New. Index(y, x : integer) : integer; var i: integer; begin New. Index: =((y-1)*XM+x) div 2); end; Function Put. Tab(y, x, value : integer) : boolean; begin if NOT ((x mod 2<>0) and (y mod 2<>0)) or NOT ((x mod 2=0) and (y mod 2=0)) then begin arrp[New. Index(y, x)]: =value; Put. Tab: =true; end else Put. Tab: =false; end; Function Get. Tab(x, y: integer) : integer; begin if ((x mod 2<>0) and (y mod 2<>0)) or ((x mod 2=0) and (y mod 2=0)) then Get. Tab: =0 else Get. Tab: =arrp[New. Index(y, x)]; end;

Пример Unit Compr. Matr; Interface Function Put. Tab(y, x, value : integer) : boolean; Function Get. Tab(x, y: integer) : integer; Procedure Init. Tab; Implementation Const XM=. . . ; Var arrp: array[1. . XM*XM div 2] of integer; desc: array[1. . XM] of integer; Procedure Init. Tab; var i : integer; begin desc[1]: =0; for i: =1 to XM do desc[i]: =desc[i-1]+XM; end; Function New. Index(y, x : integer) : integer; var i: integer; begin New. Index: =desc[y]+x div 2; end.

Разреженные массивы со случайным расположением элементов местоположения элементов со значениями отличными от фонового, не могут быть математически описаны, т. е. в их расположении нет какой-либо закономерности

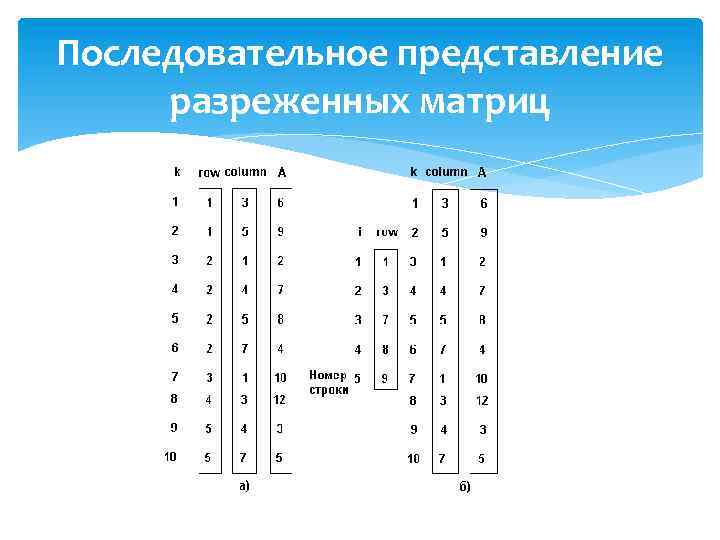Последовательное представление разреженных матриц

Представление разреженных матриц методом связанных структур Для представления разреженных матриц требуется базовая структура вершины называемая MATRIX_ELEMENT ("элемент матрицы"). Поля V, R и С каждой из этих вершин содержат соответственно значение, индексы строки и столбца элемента матрицы. Поля LEFT и UP являются указателями на следующий элемент для строки и столбца в циклическом списке, содержащем элементы матрицы. Поле LEFT указывает на вершину со следующим наименьшим номером строки.

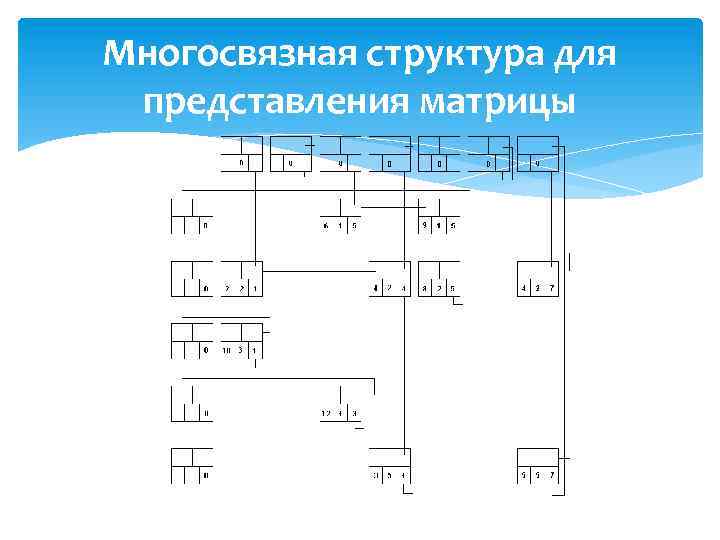Многосвязная структура для представления матрицы

Множества

Логическая структура Множество - такая структура, которая представляет собой набор неповторяющихся данных одного и того же типа. Множество может принимать все значения базового типа. Базовый тип не должен превышать 256 возможных значений. Поэтому базовым типом множества могут быть byte, char и производные от них типы

Физическая структура Множество в памяти хранится как массив битов, в котором каждый бит указывает является ли элемент принадлежащим объявленному множеству или нет. максимальное число элементов множества 256 данные типа множество могут занимать не более 32 байт. Число байтов: Byte. Size = (max div 8)-(min div 8) + 1 max и min - верхняя и нижняя границы базового типа данного множества. Номер байта: Byte. Number = (E div 8)-(min div 8) номер бита внутри этого байта по формуле: Bit. Number = E mod 8

const max=255; min=0; E=13; var S : set of byte; Byte. Size, Byte. Numb, Bit. Numb : byte; begin S: =[]; { обнуление множества } S: =S+[E]; { запись числа в множество } Byte. Size: =(max div 8)-(min div 8)+1; Bytenumb: =(E div 8)-(min div 8); Bit. Numb: =E mod 8; writeln(bytesize); { на экране 32 } writeln(bytenumb); { на экране 1 } writeln(bitnumb); { на экране 5 } end.

Числовые множества

Символьные множества S : set of char; S: =['A', 'C']; В этом случае представление множества S в памяти выглядит следующим образом : @S+0 - 0000. . . @S+31 - 0000 @S+8 - 00001010

Множество из элементов перечислимого типа Type Video=(MDA, CGA, HGC, EGAm, VGAm, SVGA, PGA, XGA); Var S : set of Video; В памяти будет занимать : Byte. Size = (9 div 8)-(0 div 8)+1=2 байта

S: =[CGA, SVGA] содержимое памяти при этом будет: @S+0 - 10000010 @S+1 - 0000

Множество от интервального типа type S=10. . 17; var I: set of S; из формулы вычисления смещения внутри байта 10 mod 8 = 2, смещение первого элемента множества I начнётся со второго бита множество этого интервала могло поместиться в один байт, оно займёт (17 div 8)-(10 div 8)+1 = 2 байта.

Операции над множествами Объединение множеств: S 2+S 3. Результатом является множество, содержащее элементы обоих исходных множеств. Пересечение множеств: S 2*S 3. Результатом является множество, содержащее общие элементы обоих исходных множеств. Проверка на вхождение элемента в множество: a in S 1. Результатом этой операции является значение логического типа - true, если элемент a входит в множество S 1, false - в противном случае.

Записи

Логическое и машинное представление записей var rec: record num : byte; { личный номер студента } name : string[20]; { Ф. И. О. } fac, group: string[7]; { факультет, группа } math, comp, lang : byte; {оценки по математике, выч. технике, ин. языку } end;

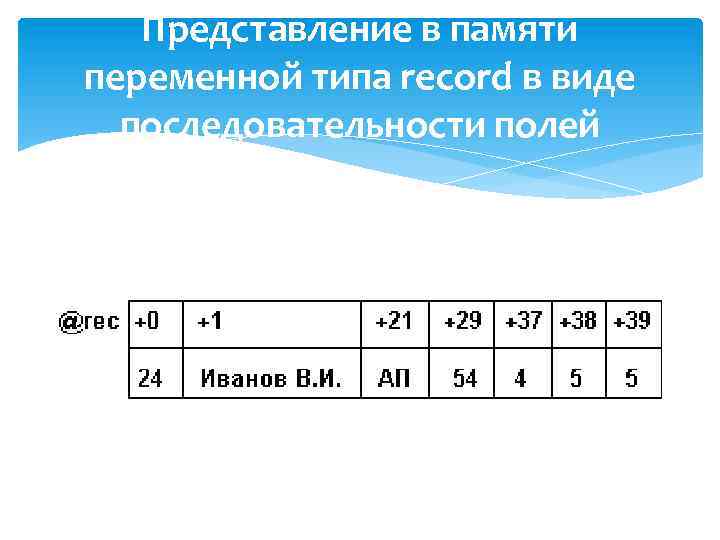Представление в памяти переменной типа record в виде последовательности полей

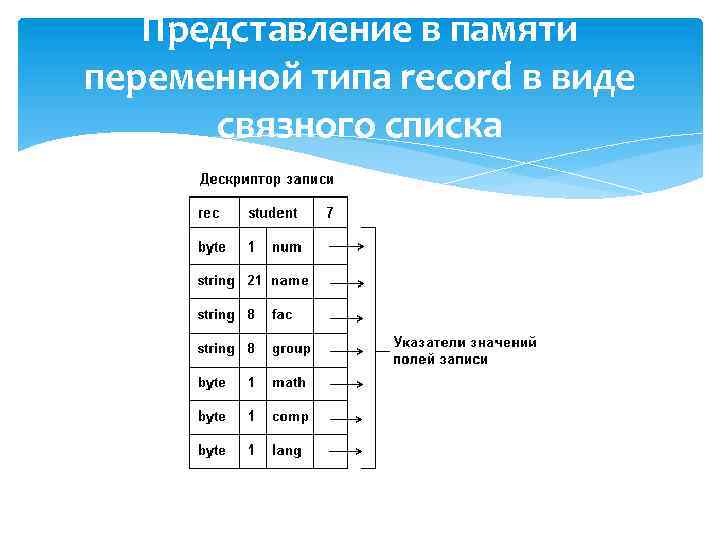Представление в памяти переменной типа record в виде связного списка

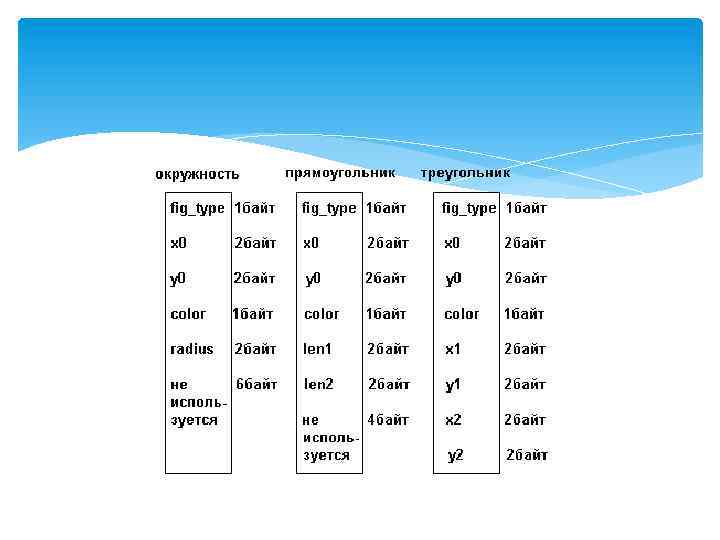
Записи с вариантами type figure = record fig_type : char; { тип фигуры } x 0, y 0 : word; { координаты опорной точки } color : byte; { цвет } case fig_t : char of 'C': ( radius : word); { радиус окружности } 'R': (len 1, len 2 : word); { длины сторон прямоугольника } 'T': (x 1, y 1, x 2, y 2 : word); { координаты двух вершин } end;

typedef struct { char fig_type; /* тип фигуры */ unsigned int x 0, y 0; /* координаты опорной точки */ unsigned char color; /* цвет */ union { struct { unsigned int radius; /* радиус окружности */ } cyrcle; struct { unsigned int len 1, len 2; /* длины сторон прямоугольника */ } rectangle; struct { unsigned int x 1, y 1, x 2, y 2; /* координаты двух вершин */ } triangle; } fig_t; } figure;

Операции логического уровня над статическими структурами

Последовательный или линейный поиск Бинарный поиск Сортировка простой выборкой Обменная сортировка простой выборкой Пузырьковая сортировка Сортировка Шелла Сортировка простыми вставками Пузырьковая сортировка вставками Турнирная сортировка Сортировка частично упорядоченным деревом Поразрядная цифровая сортировка Быстрая сортировка Хоара Сортировка попарным слиянием

1, 2, 3, 4, 5, 6, 7, 8, 9

1 -мерный массив: поиск (ф-я, процедура) 1 -мерный массив: 3 любые способа сортировки 1 -мерный массив: поиск по отсортированному массиву Массив записей : поиск Массив записей : сортировка

1, 7, 10, 12