STAT 6202 Chapter 2 2012/2013 1 CHAPTER 2























- Размер: 688.5 Кб
- Количество слайдов: 44
Описание презентации STAT 6202 Chapter 2 2012/2013 1 CHAPTER 2 по слайдам
 STAT 6202 Chapter 2 2012/2013 1 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 1 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
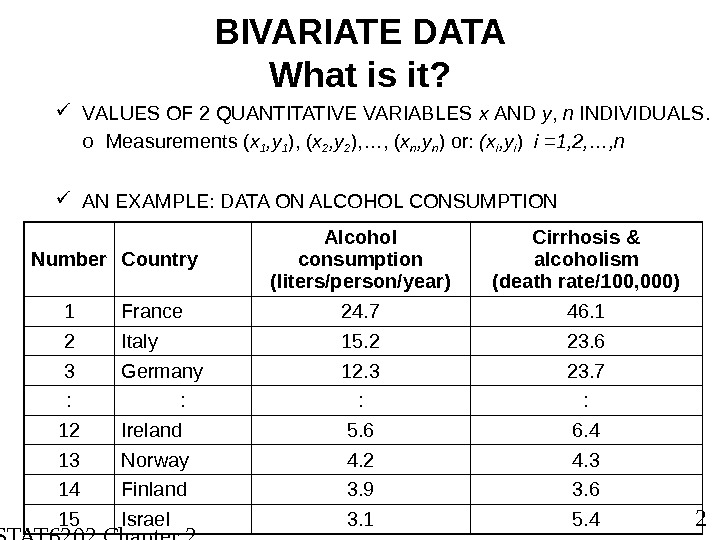
 STAT 6202 Chapter 2 2012/2013 2 BIVARIATE DATA What is it? V ALUES OF 2 QUANTITATIVE VARIABLES x AND y , n INDIVIDUALS. o Measurements ( x 1 , y 1 ), ( x 2 , y 2 ), … , ( x n , y n ) or: (x i , y i ) i =1, 2, …, n AN EXAMPLE: DATA ON ALCOHOL CONSUMPTION Number Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) 1 France 24. 7 46. 1 2 Italy 15. 2 23. 6 3 Germany 12. 3 23. 7 : : 12 Ireland 5. 6 6. 4 13 Norway 4. 2 4. 3 14 Finland 3. 9 3. 6 15 Israel 3. 1 5.
STAT 6202 Chapter 2 2012/2013 2 BIVARIATE DATA What is it? V ALUES OF 2 QUANTITATIVE VARIABLES x AND y , n INDIVIDUALS. o Measurements ( x 1 , y 1 ), ( x 2 , y 2 ), … , ( x n , y n ) or: (x i , y i ) i =1, 2, …, n AN EXAMPLE: DATA ON ALCOHOL CONSUMPTION Number Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) 1 France 24. 7 46. 1 2 Italy 15. 2 23. 6 3 Germany 12. 3 23. 7 : : 12 Ireland 5. 6 6. 4 13 Norway 4. 2 4. 3 14 Finland 3. 9 3. 6 15 Israel 3. 1 5.
 STAT 6202 Chapter 2 2012/2013 3 BIVARIATE DATA Notation 2 QUANTITATIVE VARIABLES x AND y , n INDIVIDUALS o Some old statistics, 1 )( , 2 n xx s n x x i n i iiyy n i iixx n i iiiixy ynyyy. Cxnxxx. C yxnyxyyxx. C 1 222 1 )()( ))(( 1 )( , 2 n yy s n y y i yx xy xy iixy xy ss s r n yyxx n C s 1 ))(( 1 o And some new
STAT 6202 Chapter 2 2012/2013 3 BIVARIATE DATA Notation 2 QUANTITATIVE VARIABLES x AND y , n INDIVIDUALS o Some old statistics, 1 )( , 2 n xx s n x x i n i iiyy n i iixx n i iiiixy ynyyy. Cxnxxx. C yxnyxyyxx. C 1 222 1 )()( ))(( 1 )( , 2 n yy s n y y i yx xy xy iixy xy ss s r n yyxx n C s 1 ))(( 1 o And some new
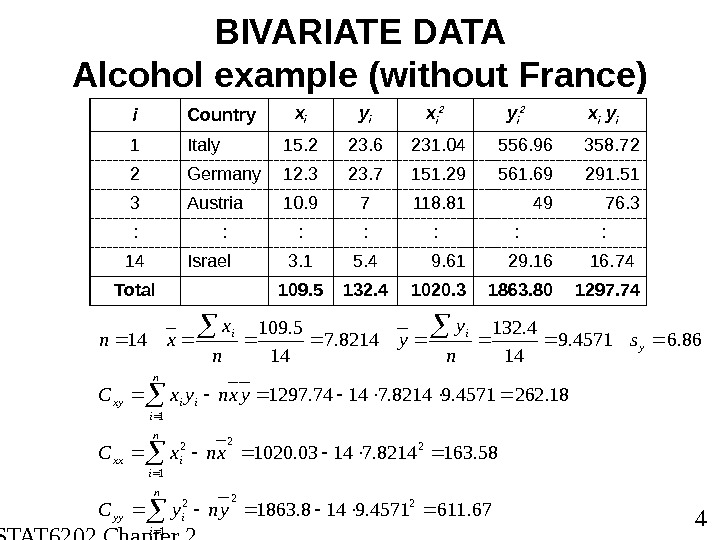
 STAT 6202 Chapter 2 2012/2013 4 BIVARIATE DATA Alcohol example (without France) n i iyy n i ixx n i iixy y ii yny. C xnx. C yxnyx. C s n y y n x xn 1 222 2 1 22 1 67. 6114571. 9148. 1863 58. 1638214. 71403. 1020 18. 2624571. 98214. 71474. 1297 86. 64571. 9 14 4. 132 8214. 7 14 5. 109 14 i Country x i y i x i 2 y i 2 x i y i 1 Italy 15. 2 23. 6 231. 04 556. 96 358. 72 2 Germany 12. 3 23. 7 151. 29 561. 69 291. 51 3 Austria 10. 9 7 118. 81 49 76. 3 : : : : 14 Israel 3. 1 5. 4 9. 61 2 9. 1 6 16. 74 Total 109. 5 132. 4 1020. 3 1863. 80 1297.
STAT 6202 Chapter 2 2012/2013 4 BIVARIATE DATA Alcohol example (without France) n i iyy n i ixx n i iixy y ii yny. C xnx. C yxnyx. C s n y y n x xn 1 222 2 1 22 1 67. 6114571. 9148. 1863 58. 1638214. 71403. 1020 18. 2624571. 98214. 71474. 1297 86. 64571. 9 14 4. 132 8214. 7 14 5. 109 14 i Country x i y i x i 2 y i 2 x i y i 1 Italy 15. 2 23. 6 231. 04 556. 96 358. 72 2 Germany 12. 3 23. 7 151. 29 561. 69 291. 51 3 Austria 10. 9 7 118. 81 49 76. 3 : : : : 14 Israel 3. 1 5. 4 9. 61 2 9. 1 6 16. 74 Total 109. 5 132. 4 1020. 3 1863. 80 1297.
 STAT 6202 Chapter 2 2012/2013 5 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 5 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
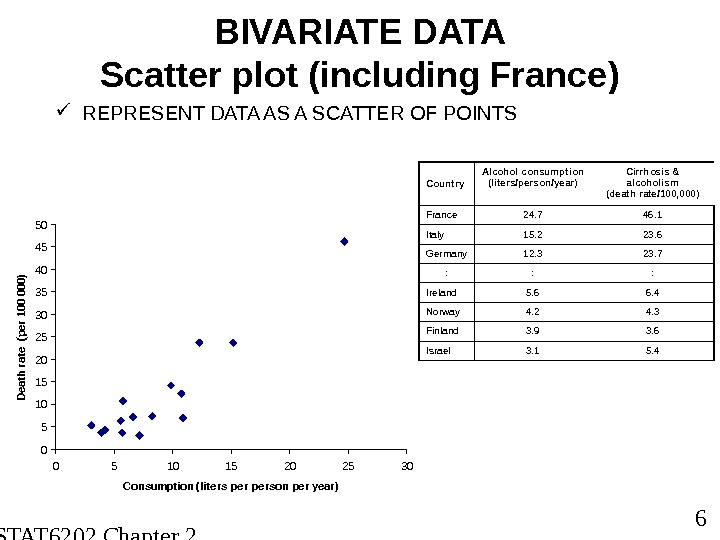
 STAT 6202 Chapter 2 2012/2013 6 BIVARIATE DATA Scatter plot (including France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) France 24. 7 46. 1 Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 05101520253035404550 0 5 10 15 20 25 30 Consumption (liters person per year)Death rate (per 100 000)
STAT 6202 Chapter 2 2012/2013 6 BIVARIATE DATA Scatter plot (including France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) France 24. 7 46. 1 Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 05101520253035404550 0 5 10 15 20 25 30 Consumption (liters person per year)Death rate (per 100 000)
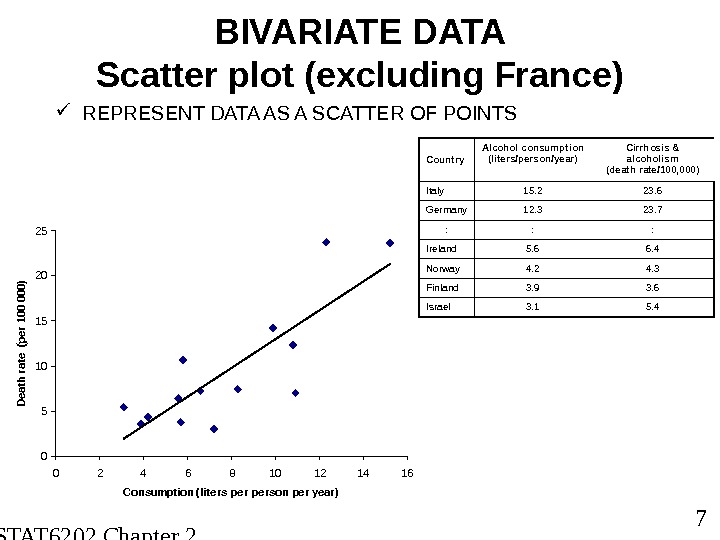
 STAT 6202 Chapter 2 2012/2013 7 BIVARIATE DATA Scatter plot (excluding France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000)
STAT 6202 Chapter 2 2012/2013 7 BIVARIATE DATA Scatter plot (excluding France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000)
 STAT 6202 Chapter 2 2012/2013 8 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 8 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
 STAT 6202 Chapter 2 2012/2013 9 REGRESSION What is it? It’s everywhere! TRYING TO PREDICT (/EXPLAIN) ONE VARIABLE AS A FUNCTION OF ANOTHER ONE o Or multiple other ones ONE OF THE MOST OFTEN USED STATISTICAL TOOLS REGRESSION CAN BE VERY POWERFUL AND COMPLEX WE WILL LOOK AT THE MOST BASIC o Simple linear regression: Linear relationship between two variables
STAT 6202 Chapter 2 2012/2013 9 REGRESSION What is it? It’s everywhere! TRYING TO PREDICT (/EXPLAIN) ONE VARIABLE AS A FUNCTION OF ANOTHER ONE o Or multiple other ones ONE OF THE MOST OFTEN USED STATISTICAL TOOLS REGRESSION CAN BE VERY POWERFUL AND COMPLEX WE WILL LOOK AT THE MOST BASIC o Simple linear regression: Linear relationship between two variables
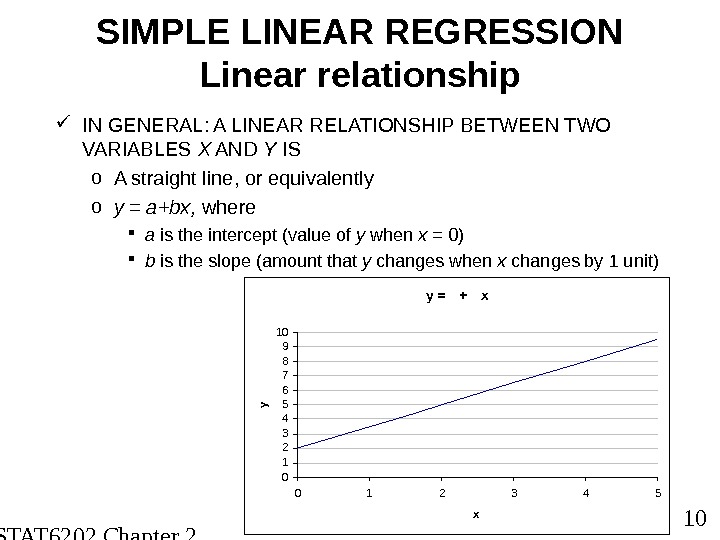
 STAT 6202 Chapter 2 2012/2013 10 SIMPLE LINEAR REGRESSION Linear relationship IN GENERAL: A LINEAR RELATIONSHIP BETWEEN TWO VARIABLES X AND Y IS o A straight line, or equivalently o y = a+bx, where a is the intercept (value of y when x = 0) b is the slope (amount that y changes when x changes by 1 unit) y = + x 012345678910 0 1 2 3 4 5 xy
STAT 6202 Chapter 2 2012/2013 10 SIMPLE LINEAR REGRESSION Linear relationship IN GENERAL: A LINEAR RELATIONSHIP BETWEEN TWO VARIABLES X AND Y IS o A straight line, or equivalently o y = a+bx, where a is the intercept (value of y when x = 0) b is the slope (amount that y changes when x changes by 1 unit) y = + x 012345678910 0 1 2 3 4 5 xy
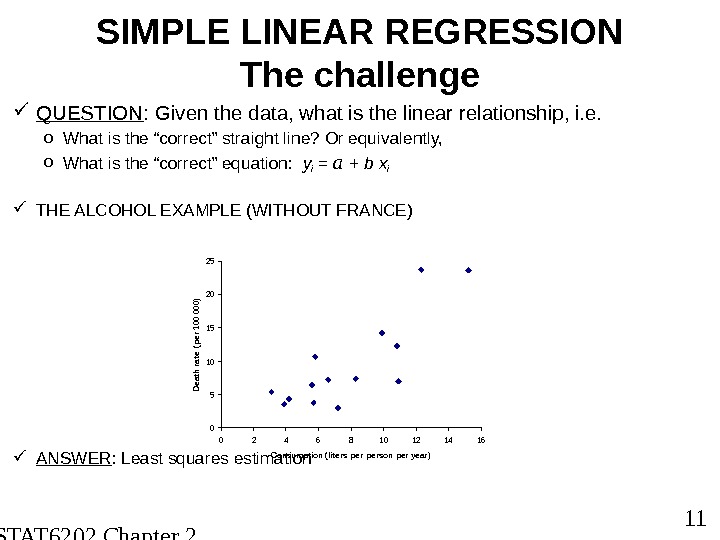
 STAT 6202 Chapter 2 2012/2013 11 SIMPLE LINEAR REGRESSION The challenge QUESTION : Given the data, what is the linear relationship, i. e. o What is the “correct” straight line? Or equivalently, o What is the “correct” equation: y i = a + b x i THE ALCOHOL EXAMPLE (WITHOUT FRANCE) ANSWER : Least squares estimation 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000)
STAT 6202 Chapter 2 2012/2013 11 SIMPLE LINEAR REGRESSION The challenge QUESTION : Given the data, what is the linear relationship, i. e. o What is the “correct” straight line? Or equivalently, o What is the “correct” equation: y i = a + b x i THE ALCOHOL EXAMPLE (WITHOUT FRANCE) ANSWER : Least squares estimation 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000)
 STAT 6202 Chapter 2 2012/2013 12 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 12 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
 STAT 6202 Chapter 2 2012/2013 13 SIMPLE LINEAR REGRESSION Least Squares Estimation COMPUTING THE STRAIGHT LINE WHICH IS CLOSER TO THE DATA POINTS THAN ANY OTHER LINE MINIMIZING THE SUM OF SQUARED RESIDUALS n i ii n i ibxaye 1 2 )( xbya C C b xx xy Estimated change in mean y for a 1 unit increase in x Estimated mean y for x = 0 LEAST SQUARES ESTIMATORS AR
STAT 6202 Chapter 2 2012/2013 13 SIMPLE LINEAR REGRESSION Least Squares Estimation COMPUTING THE STRAIGHT LINE WHICH IS CLOSER TO THE DATA POINTS THAN ANY OTHER LINE MINIMIZING THE SUM OF SQUARED RESIDUALS n i ii n i ibxaye 1 2 )( xbya C C b xx xy Estimated change in mean y for a 1 unit increase in x Estimated mean y for x = 0 LEAST SQUARES ESTIMATORS AR
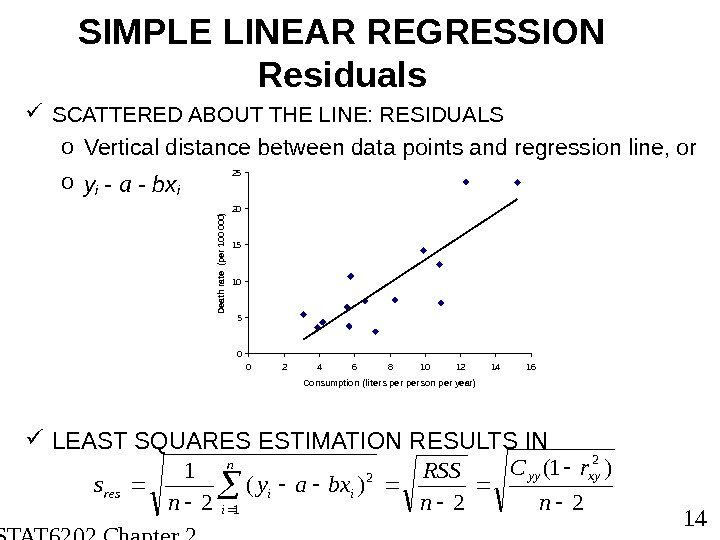
 STAT 6202 Chapter 2 2012/2013 14 SIMPLE LINEAR REGRESSION Residuals SCATTERED ABOUT THE LINE: RESIDUALS o Vertical distance between data points and regression line, or o yi — a — bxi 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters per pe rson per year) Death rate (per 100 000) 2 )1( 2 )( 2 1 2 n r. C n RSS bxay n s xyyy n i iires LEAST SQUARES ESTIMATION RESULTS IN
STAT 6202 Chapter 2 2012/2013 14 SIMPLE LINEAR REGRESSION Residuals SCATTERED ABOUT THE LINE: RESIDUALS o Vertical distance between data points and regression line, or o yi — a — bxi 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters per pe rson per year) Death rate (per 100 000) 2 )1( 2 )( 2 1 2 n r. C n RSS bxay n s xyyy n i iires LEAST SQUARES ESTIMATION RESULTS IN
 STAT 6202 Chapter 2 2012/2013 15 SIMPLE LINEAR REGRESSION The alcohol example (without France) LEAST SQUARES ESTIMATES ARE ESTIMATED LINEAR REGRESSION EQUATION -3. 0786 + 1. 6027 xi 0786. 38214. 76027. 14571. 9 6027. 1 58. 163 18. 262 xbya C C b xx xy
STAT 6202 Chapter 2 2012/2013 15 SIMPLE LINEAR REGRESSION The alcohol example (without France) LEAST SQUARES ESTIMATES ARE ESTIMATED LINEAR REGRESSION EQUATION -3. 0786 + 1. 6027 xi 0786. 38214. 76027. 14571. 9 6027. 1 58. 163 18. 262 xbya C C b xx xy
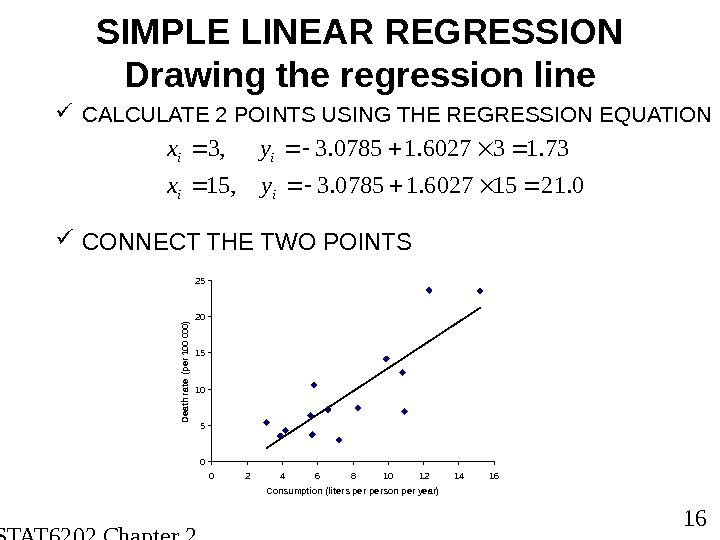
 STAT 6202 Chapter 2 2012/2013 16 SIMPLE LINEAR REGRESSION Drawing the regression line CALCULATE 2 POINTS USING THE REGRESSION EQUATION 0510152025 0 2 4 6 8 10 12 14 16 Consumption (lite rs person per year)Death rate (per 100 000) 0. 21156027. 10785. 3, 15 73. 136027. 10785. 3, 3 ii ii yx yx CONNECT THE TWO POINTS
STAT 6202 Chapter 2 2012/2013 16 SIMPLE LINEAR REGRESSION Drawing the regression line CALCULATE 2 POINTS USING THE REGRESSION EQUATION 0510152025 0 2 4 6 8 10 12 14 16 Consumption (lite rs person per year)Death rate (per 100 000) 0. 21156027. 10785. 3, 15 73. 136027. 10785. 3, 3 ii ii yx yx CONNECT THE TWO POINTS
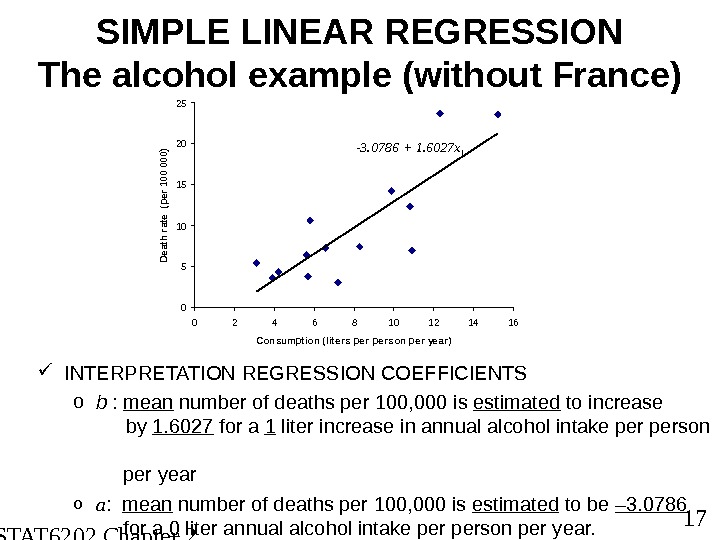
 STAT 6202 Chapter 2 2012/2013 17 SIMPLE LINEAR REGRESSION The alcohol example (without France) INTERPRETATION REGRESSION COEFFICIENTS o b : mean number of deaths per 100, 000 is estimated to increase by 1. 6027 for a 1 liter increase in annual alcohol intake person per year o a : mean number of deaths per 100, 000 is estimated to be – 3. 0786 for a 0 liter annual alcohol intake person per year. 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000) -3. 0786 + 1. 6027 x i
STAT 6202 Chapter 2 2012/2013 17 SIMPLE LINEAR REGRESSION The alcohol example (without France) INTERPRETATION REGRESSION COEFFICIENTS o b : mean number of deaths per 100, 000 is estimated to increase by 1. 6027 for a 1 liter increase in annual alcohol intake person per year o a : mean number of deaths per 100, 000 is estimated to be – 3. 0786 for a 0 liter annual alcohol intake person per year. 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000) -3. 0786 + 1. 6027 x i
 STAT 6202 Chapter 2 2012/2013 18 SIMPLE LINEAR REGRESSION Prediction WHAT IS THE EXPECTED DEATH RATE FOR AN ANNUAL ALCOHOL INTAKE OF 15 LITERS P. P. PER YEAR? o Don’t read from graph, use the regression equation o Answer: 21. 0 deaths per 100, 000 people WHAT IS THE STANDARD DEVIATION OF THE DEATH RATE FOR A GIVEN LEVEL OF ALCOHOL INTAKE? 98. 3 12 )83. 01(67. 611 2 )1( 2 22 n r. C n RSS s xyyy res )0. 21156027. 10785. 3, 15(iiyx
STAT 6202 Chapter 2 2012/2013 18 SIMPLE LINEAR REGRESSION Prediction WHAT IS THE EXPECTED DEATH RATE FOR AN ANNUAL ALCOHOL INTAKE OF 15 LITERS P. P. PER YEAR? o Don’t read from graph, use the regression equation o Answer: 21. 0 deaths per 100, 000 people WHAT IS THE STANDARD DEVIATION OF THE DEATH RATE FOR A GIVEN LEVEL OF ALCOHOL INTAKE? 98. 3 12 )83. 01(67. 611 2 )1( 2 22 n r. C n RSS s xyyy res )0. 21156027. 10785. 3, 15(iiyx
 STAT 6202 Chapter 2 2012/2013 19 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 19 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
 STAT 6202 Chapter 2 2012/2013 20 SIMPLE LINEAR REGRESSION Watch out! YOU CAN ALWAYS DRAW A REGRESSION LINE, BUT o Not always appropriate/good fity x o Relationship does not necessarily hold outside range Average death rate for alcohol intake of 1 liter p. p. p. y? o Regression causality Drawing a line does not prove that one variable is causing a change in another one Causality could be the case, but just a line is not proof There can be confounding variables An example: national ice cream sales and my mood
STAT 6202 Chapter 2 2012/2013 20 SIMPLE LINEAR REGRESSION Watch out! YOU CAN ALWAYS DRAW A REGRESSION LINE, BUT o Not always appropriate/good fity x o Relationship does not necessarily hold outside range Average death rate for alcohol intake of 1 liter p. p. p. y? o Regression causality Drawing a line does not prove that one variable is causing a change in another one Causality could be the case, but just a line is not proof There can be confounding variables An example: national ice cream sales and my mood
 STAT 6202 Chapter 2 2012/2013 21 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 21 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
 STAT 6202 Chapter 2 2012/2013 22 LOG TRANSFORMS IN REGRESSION Why/When? When natural comparisons are in terms of ratios. REMEMBER: LOG APPROXIMATION PROPERTY o Difference between two numbers, as a fraction of their mean, approximately equals difference between their natural logs: o This works well for fractional differences up to 0. 5 20067. 0)90(log)110(log 20. 0 100 90110 10008. 0)95(log)105(log 10. 0 100 95105 ee ee
STAT 6202 Chapter 2 2012/2013 22 LOG TRANSFORMS IN REGRESSION Why/When? When natural comparisons are in terms of ratios. REMEMBER: LOG APPROXIMATION PROPERTY o Difference between two numbers, as a fraction of their mean, approximately equals difference between their natural logs: o This works well for fractional differences up to 0. 5 20067. 0)90(log)110(log 20. 0 100 90110 10008. 0)95(log)105(log 10. 0 100 95105 ee ee
 STAT 6202 Chapter 2 2012/2013 23 LOG TRANSFORMS IN REGRESSION Why/When? When natural comparisons are in terms of ratios. When data vary over several orders of magniture. For transforming a positively skewed distribution to a more symmetric scale. o An example: the handbook of Biological Statistics ( http: // udel. edu /~ mcdonald / stattransform. html ) Eastern mudminnow (Umbra pygmaea).
STAT 6202 Chapter 2 2012/2013 23 LOG TRANSFORMS IN REGRESSION Why/When? When natural comparisons are in terms of ratios. When data vary over several orders of magniture. For transforming a positively skewed distribution to a more symmetric scale. o An example: the handbook of Biological Statistics ( http: // udel. edu /~ mcdonald / stattransform. html ) Eastern mudminnow (Umbra pygmaea).
 STAT 6202 Chapter 2 2012/2013 24 LOG TRANSFORMS IN REGRESSION Why/When? When natural comparisons are in terms of ratios. When data vary over several orders of magniture. For transforming a positively skewed distribution to a more symmetric scale. For making relationships more linear:
STAT 6202 Chapter 2 2012/2013 24 LOG TRANSFORMS IN REGRESSION Why/When? When natural comparisons are in terms of ratios. When data vary over several orders of magniture. For transforming a positively skewed distribution to a more symmetric scale. For making relationships more linear:
 STAT 6202 Chapter 2 2012/2013 25 PREVIOUSLY WE SAW FOR y = a + bx o Least square estimates: o Interpretations: b : mean y is estimated to increase by b for a 1 unit increase in x a : mean y is estimated to be a when x is 0 THE ABOVE NEEDS TO BE ‘TRANSLATED’ FOR TRANSFORMATIONS AN EXAMPLE: y = a + bz, where z=log(x) o Least square estimates: o Interpretations: b : mean y is estimated to increase by b for a 1 unit increase in z a : mean y is estimated to be a when z is 0, i. e. mean y is estimated to be a when x is 1 LOG TRANSFORMS IN REGRESSION Pay attention to the followingxbya. CCbxxxy, / zbya. CCbzzzy, /
STAT 6202 Chapter 2 2012/2013 25 PREVIOUSLY WE SAW FOR y = a + bx o Least square estimates: o Interpretations: b : mean y is estimated to increase by b for a 1 unit increase in x a : mean y is estimated to be a when x is 0 THE ABOVE NEEDS TO BE ‘TRANSLATED’ FOR TRANSFORMATIONS AN EXAMPLE: y = a + bz, where z=log(x) o Least square estimates: o Interpretations: b : mean y is estimated to increase by b for a 1 unit increase in z a : mean y is estimated to be a when z is 0, i. e. mean y is estimated to be a when x is 1 LOG TRANSFORMS IN REGRESSION Pay attention to the followingxbya. CCbxxxy, / zbya. CCbzzzy, /
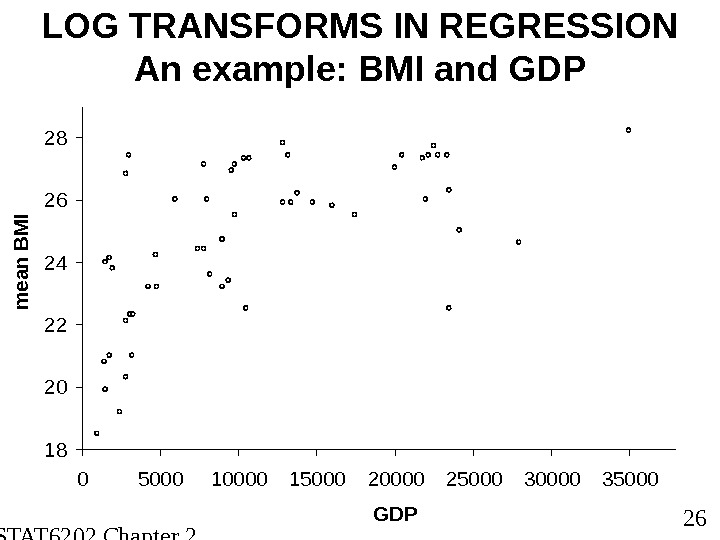
 STAT 6202 Chapter 2 2012/2013 26 LOG TRANSFORMS IN REGRESSION An example: BMI and GDP 18202224262830 0 5000 10000 15000 20000 25000 30000 35000 40000 GDPm e a n B M I
STAT 6202 Chapter 2 2012/2013 26 LOG TRANSFORMS IN REGRESSION An example: BMI and GDP 18202224262830 0 5000 10000 15000 20000 25000 30000 35000 40000 GDPm e a n B M I
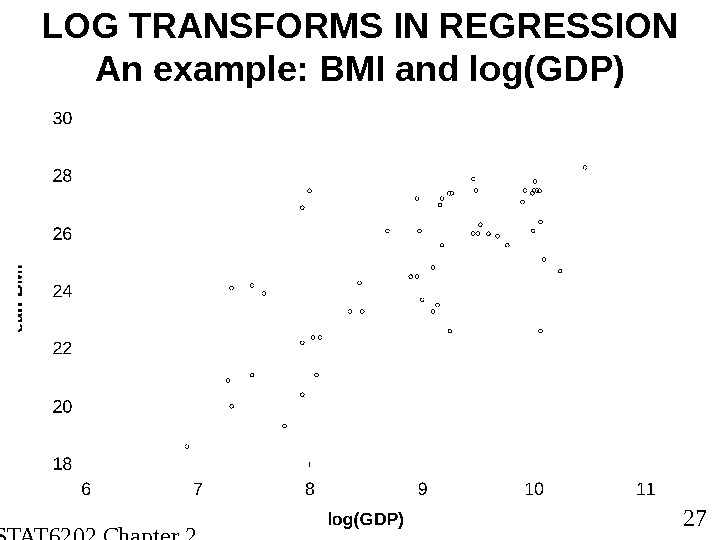
 STAT 6202 Chapter 2 2012/2013 27 LOG TRANSFORMS IN REGRESSION An example: BMI and log(GDP)
STAT 6202 Chapter 2 2012/2013 27 LOG TRANSFORMS IN REGRESSION An example: BMI and log(GDP)
 STAT 6202 Chapter 2 2012/2013 28 LOG TRANSFORMS IN REGRESSION An example: BMI and GDP DATA FOR BMI (kg/m 2 ) AND GDP FOR DIFFERENT COUNTRIES PREDICT BMI FOR COUNTRY WITH GDP OF 4000 APPLYING LOG-TRANSFORMATION MIGHT BE USEFUL REGRESSION EQUATION FOR BMI ON LOG(GDP) LOG e (4000)=8. 29, SO PREDICTED BMI IS BMI = 6. 89 + 2 · log e (4000) = 23. 5 BMI = 6. 89 + 2 · log e (GDP)
STAT 6202 Chapter 2 2012/2013 28 LOG TRANSFORMS IN REGRESSION An example: BMI and GDP DATA FOR BMI (kg/m 2 ) AND GDP FOR DIFFERENT COUNTRIES PREDICT BMI FOR COUNTRY WITH GDP OF 4000 APPLYING LOG-TRANSFORMATION MIGHT BE USEFUL REGRESSION EQUATION FOR BMI ON LOG(GDP) LOG e (4000)=8. 29, SO PREDICTED BMI IS BMI = 6. 89 + 2 · log e (4000) = 23. 5 BMI = 6. 89 + 2 · log e (GDP)
 STAT 6202 Chapter 2 2012/2013 29 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 29 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Watch out! o Log transformation and regression o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
 STAT 6202 Chapter 2 2012/2013 30 SIMPLE LINEAR REGRESSION A practical approach 1. DRAW A SCATTER PLOT 2. THINK OF POTENTIAL USEFUL TRANSFORMATIONS 3. TRANSFORM VARIABLES 4. SELECT VARIABLES WITH STRONGEST LINEAR RELATIONSHIP BY 1. Comparing scatterplots of original and transformed variables 2. Comparing correlation coefficients of original and transformed variables 5. USE VARIABLES WITH STRONGEST LINEAR RELATIONSHIP 6. CALCULATE REGRESSION EQUATION USING LEAST SQUARES ESTIMATION In this course we consider the following 4 options: a. y = a + b • x b. log e (y) = a + b • x c. y = a + b • log e (x) d. log e (y) = a + b • log e (x) ) 7. USE REGRESSION EQUATION FOR PREDICTION
STAT 6202 Chapter 2 2012/2013 30 SIMPLE LINEAR REGRESSION A practical approach 1. DRAW A SCATTER PLOT 2. THINK OF POTENTIAL USEFUL TRANSFORMATIONS 3. TRANSFORM VARIABLES 4. SELECT VARIABLES WITH STRONGEST LINEAR RELATIONSHIP BY 1. Comparing scatterplots of original and transformed variables 2. Comparing correlation coefficients of original and transformed variables 5. USE VARIABLES WITH STRONGEST LINEAR RELATIONSHIP 6. CALCULATE REGRESSION EQUATION USING LEAST SQUARES ESTIMATION In this course we consider the following 4 options: a. y = a + b • x b. log e (y) = a + b • x c. y = a + b • log e (x) d. log e (y) = a + b • log e (x) ) 7. USE REGRESSION EQUATION FOR PREDICTION
 STAT 6202 Chapter 2 2012/2013 31 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Log transformation and regression o Watch out! o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 31 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Log transformation and regression o Watch out! o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
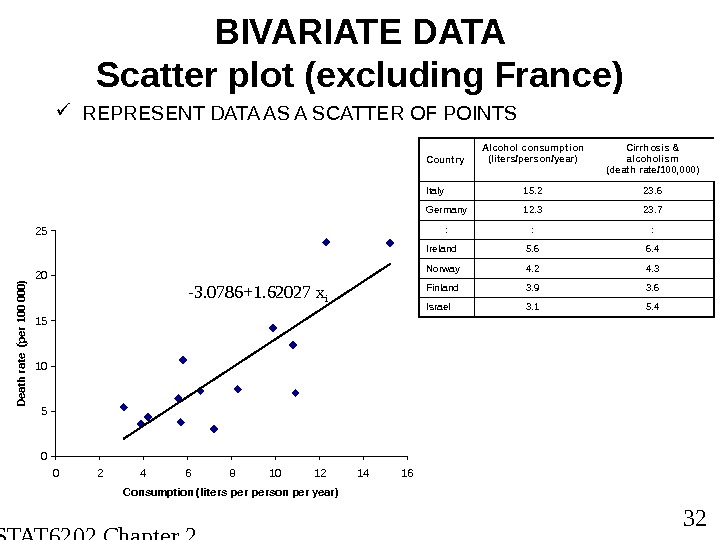
 STAT 6202 Chapter 2 2012/2013 32 BIVARIATE DATA Scatter plot (excluding France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000) -3. 0786+1. 62027 x i
STAT 6202 Chapter 2 2012/2013 32 BIVARIATE DATA Scatter plot (excluding France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000) -3. 0786+1. 62027 x i
 STAT 6202 Chapter 2 2012/2013 33 CORRELATION COEFFICIENT The theory CORRELATION COEFFICIENT MEASURES THE STRENGTH OF A LINEAR RELATIONSHIP BETWEEN TWO VARIABLES FORMULA: SOME PROPERTIES o – 1 ≤ r xy ≤ 1 o r xy > 0: y tends to increase as x increases and vice versa o r xy < 0: y tends to decrease as x increases and vice versa o r xy =1 or r xy =-1: all points (x 1 , y i ) lie on a straight line o the further r xy is away from 0, the closer the points are to a straight line o | r xy | is not affected by linear transformations yx xy yyxx xy xy ss s CC C r
STAT 6202 Chapter 2 2012/2013 33 CORRELATION COEFFICIENT The theory CORRELATION COEFFICIENT MEASURES THE STRENGTH OF A LINEAR RELATIONSHIP BETWEEN TWO VARIABLES FORMULA: SOME PROPERTIES o – 1 ≤ r xy ≤ 1 o r xy > 0: y tends to increase as x increases and vice versa o r xy < 0: y tends to decrease as x increases and vice versa o r xy =1 or r xy =-1: all points (x 1 , y i ) lie on a straight line o the further r xy is away from 0, the closer the points are to a straight line o | r xy | is not affected by linear transformations yx xy yyxx xy xy ss s CC C r
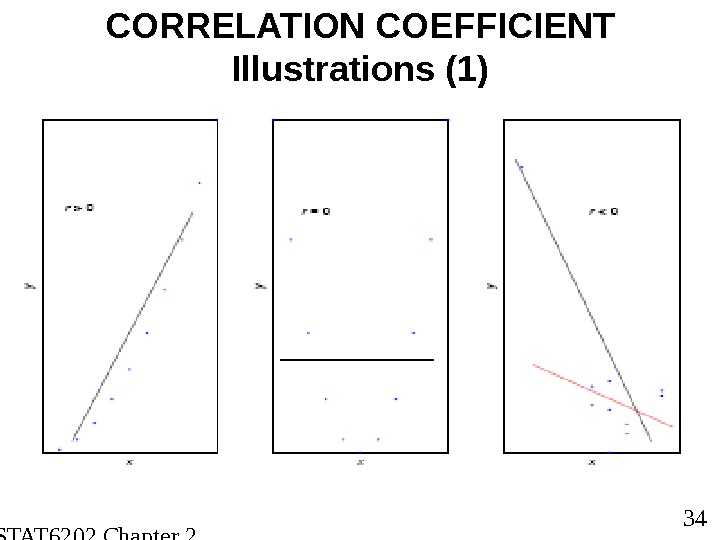
 STAT 6202 Chapter 2 2012/2013 34 CORRELATION COEFFICIENT Illustrations (1)
STAT 6202 Chapter 2 2012/2013 34 CORRELATION COEFFICIENT Illustrations (1)
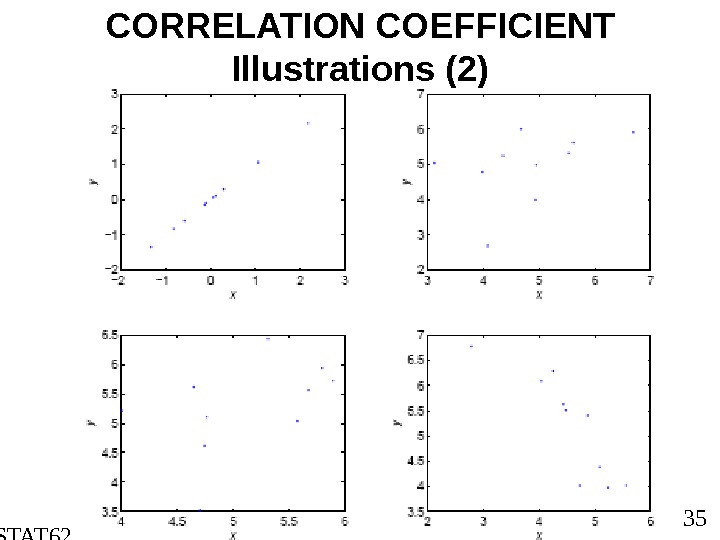
 STAT 6202 Chapter 2 2012/2013 35 CORRELATION COEFFICIENT Illustrations (2)
STAT 6202 Chapter 2 2012/2013 35 CORRELATION COEFFICIENT Illustrations (2)
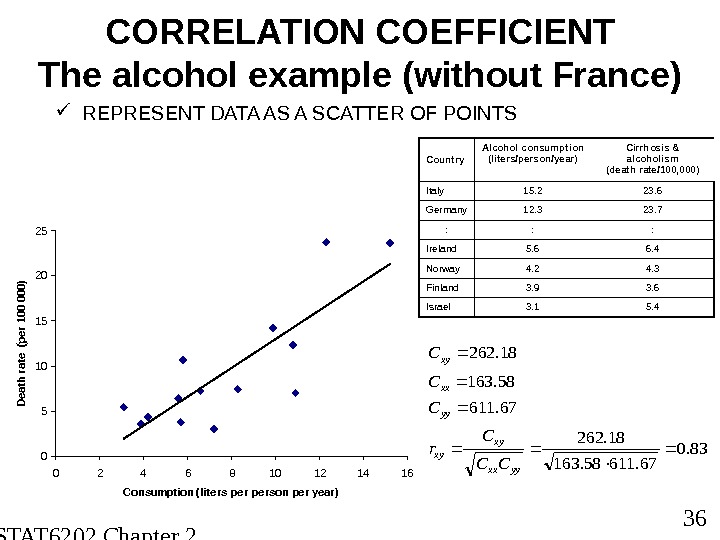
 STAT 6202 Chapter 2 2012/2013 36 CORRELATION COEFFICIENT The alcohol example (without France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000) 83. 0 67. 61158. 163 18. 262 67. 611 58. 163 18. 262 yyxx xy xy yy xx xy CC C r
STAT 6202 Chapter 2 2012/2013 36 CORRELATION COEFFICIENT The alcohol example (without France) REPRESENT DATA AS A SCATTER OF POINTS Country Alcohol consumption (liters/person/year) Cirrhosis & alcoholism (death rate/100, 000) Italy 15. 2 23. 6 Germany 12. 3 23. 7 : : : Ireland 5. 6 6. 4 Norway 4. 2 4. 3 Finland 3. 9 3. 6 Israel 3. 1 5. 4 0510152025 0 2 4 6 8 10 12 14 16 Consumption (liters person per year)Death rate (per 100 000) 83. 0 67. 61158. 163 18. 262 67. 611 58. 163 18. 262 yyxx xy xy yy xx xy CC C r
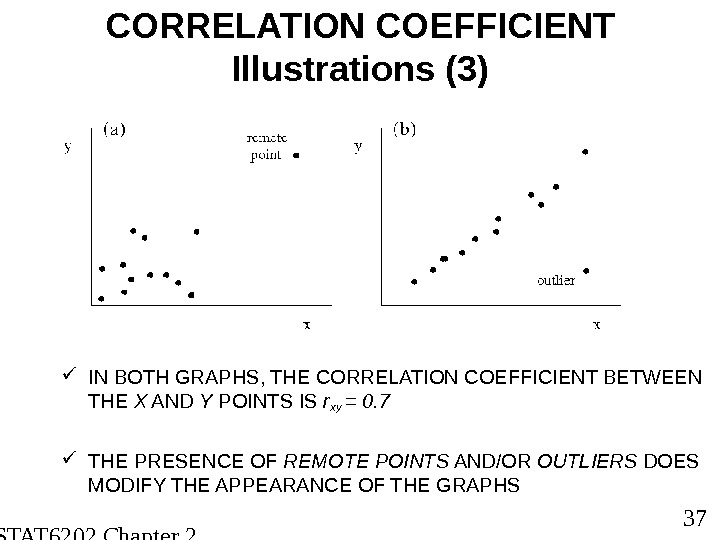
 STAT 6202 Chapter 2 2012/2013 37 CORRELATION COEFFICIENT Illustrations (3) IN BOTH GRAPHS, THE CORRELATION COEFFICIENT BETWEEN THE X AND Y POINTS IS r xy = 0. 7 THE PRESENCE OF REMOTE POINTS AND/OR OUTLIERS DOES MODIFY THE APPEARANCE OF THE GRAPHS
STAT 6202 Chapter 2 2012/2013 37 CORRELATION COEFFICIENT Illustrations (3) IN BOTH GRAPHS, THE CORRELATION COEFFICIENT BETWEEN THE X AND Y POINTS IS r xy = 0. 7 THE PRESENCE OF REMOTE POINTS AND/OR OUTLIERS DOES MODIFY THE APPEARANCE OF THE GRAPHS
 STAT 6202 Chapter 2 2012/2013 38 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Log transformation and regression o Watch out! o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
STAT 6202 Chapter 2 2012/2013 38 CHAPTER 2 Describing bivariate data NOTATION SCATTER PLOT SIMPLE LINEAR REGRESSION o What is it? o Least squares estimation o Log transformation and regression o Watch out! o A practical approach SAMPLE CORRELATION COEFFICIENT RANK CORRELATION COEFICIENT
 STAT 6202 Chapter 2 2012/2013 39 SPEARMAN’s CORRELATION COEFFICIENT The theory SPEARMAN’S RANK CORRELATION COEFFICIENT, r s , MEASURES THE STRENGHT OF THE LINEAR RELATIONSHIP BETWEEN ORDERINGS OF 2 VARIABLES FORMULA: o Where d i is the difference between the rank of x i and the rank of y i )1( 6 12 1 2 nn d r n i i S PROPERTIES (SIMILAR TO r xy ) – 1 ≤ r s ≤ 1 o r s > 0: y tends to increase as x increases and vice versa o r s < 0: y tends to decrease as x increases and vice versa o the further r s is away from 0, the stronger the relationship o | r s | is not affected by linear transformations
STAT 6202 Chapter 2 2012/2013 39 SPEARMAN’s CORRELATION COEFFICIENT The theory SPEARMAN’S RANK CORRELATION COEFFICIENT, r s , MEASURES THE STRENGHT OF THE LINEAR RELATIONSHIP BETWEEN ORDERINGS OF 2 VARIABLES FORMULA: o Where d i is the difference between the rank of x i and the rank of y i )1( 6 12 1 2 nn d r n i i S PROPERTIES (SIMILAR TO r xy ) – 1 ≤ r s ≤ 1 o r s > 0: y tends to increase as x increases and vice versa o r s < 0: y tends to decrease as x increases and vice versa o the further r s is away from 0, the stronger the relationship o | r s | is not affected by linear transformations
 STAT 6202 Chapter 2 2012/2013 40 RANKING DATA/OBSERVATIONS How to go about it? RANKING DATA o Put n observations in ascending order o Assign each observation its order number from 1 to n o Rank: For unique observations: the order number For identical observations: the average order number AN EXAMPLE: 20 40 30 20 10 20 30 o Order data: 10 20 20 30 40 o Assign order number: 1 2 3 4 5 6 7 o Final rank: 1 3 3 3 5. 5 7 2 + 3 + 4 3 5 +
STAT 6202 Chapter 2 2012/2013 40 RANKING DATA/OBSERVATIONS How to go about it? RANKING DATA o Put n observations in ascending order o Assign each observation its order number from 1 to n o Rank: For unique observations: the order number For identical observations: the average order number AN EXAMPLE: 20 40 30 20 10 20 30 o Order data: 10 20 20 30 40 o Assign order number: 1 2 3 4 5 6 7 o Final rank: 1 3 3 3 5. 5 7 2 + 3 + 4 3 5 +
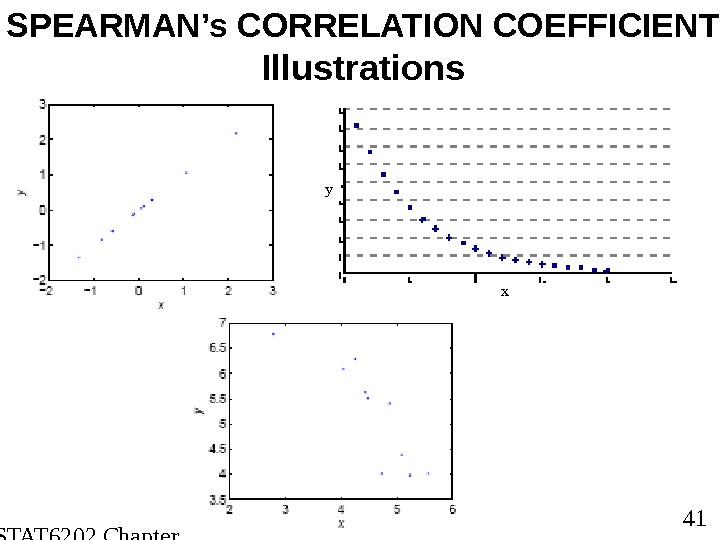
 STAT 6202 Chapter 2 2012/2013 41 SPEARMAN’s CORRELATION COEFFICIENT Illustrations xy
STAT 6202 Chapter 2 2012/2013 41 SPEARMAN’s CORRELATION COEFFICIENT Illustrations xy
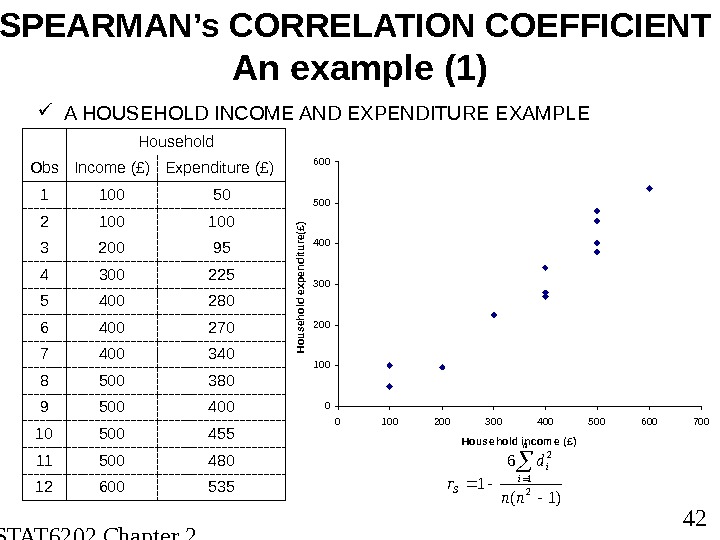
 STAT 6202 Chapter 2 2012/2013 42 SPEARMAN’s CORRELATION COEFFICIENT An example (1) A HOUSEHOLD INCOME AND EXPENDITURE EXAMPLE Household Obs Income (£) Expenditure (£) 1 100 50 2 100 3 200 95 4 300 225 5 400 280 6 400 270 7 400 340 8 500 380 9 500 400 10 500 455 11 500 480 12 600 535)1( 6 1 2 nn d r n i i S 0100200300400500600 0 100 200 300 400 500 600 700 Hous e hold incom e (£) Household expenditure(£)
STAT 6202 Chapter 2 2012/2013 42 SPEARMAN’s CORRELATION COEFFICIENT An example (1) A HOUSEHOLD INCOME AND EXPENDITURE EXAMPLE Household Obs Income (£) Expenditure (£) 1 100 50 2 100 3 200 95 4 300 225 5 400 280 6 400 270 7 400 340 8 500 380 9 500 400 10 500 455 11 500 480 12 600 535)1( 6 1 2 nn d r n i i S 0100200300400500600 0 100 200 300 400 500 600 700 Hous e hold incom e (£) Household expenditure(£)
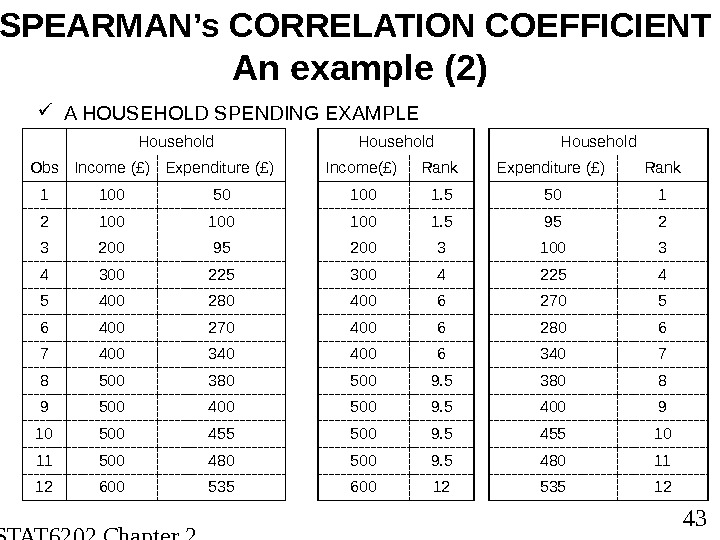
 STAT 6202 Chapter 2 2012/2013 43 SPEARMAN’s CORRELATION COEFFICIENT An example (2) A HOUSEHOLD SPENDING EXAMPLE Household Obs Income (£) Expenditure (£) 1 100 50 2 100 3 200 95 4 300 225 5 400 280 6 400 270 7 400 340 8 500 380 9 500 400 10 500 455 11 500 480 12 600 535 Household Income (£) Rank 100 1. 5 200 3 300 4 400 6 500 9. 5 600 12 Household Expenditure (£) Rank
STAT 6202 Chapter 2 2012/2013 43 SPEARMAN’s CORRELATION COEFFICIENT An example (2) A HOUSEHOLD SPENDING EXAMPLE Household Obs Income (£) Expenditure (£) 1 100 50 2 100 3 200 95 4 300 225 5 400 280 6 400 270 7 400 340 8 500 380 9 500 400 10 500 455 11 500 480 12 600 535 Household Income (£) Rank 100 1. 5 200 3 300 4 400 6 500 9. 5 600 12 Household Expenditure (£) Rank
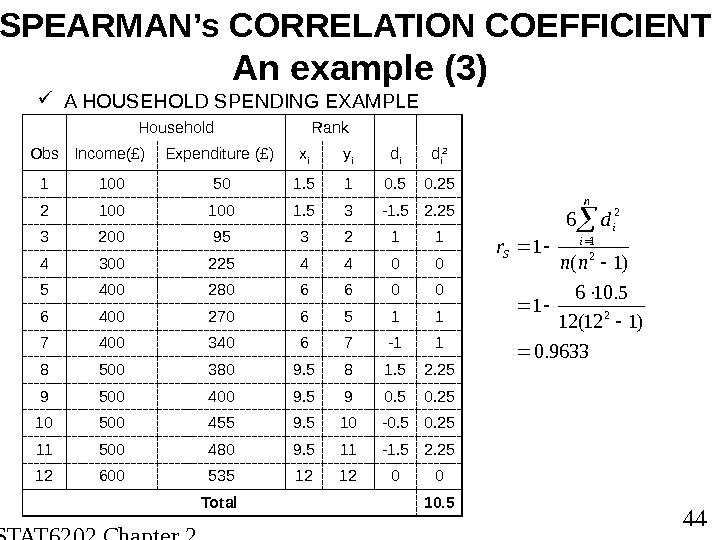
 STAT 6202 Chapter 2 2012/2013 44 SPEARMAN’s CORRELATION COEFFICIENT An example (3) A HOUSEHOLD SPENDING EXAMPLE Household Rank Obs Income (£) Expenditure (£) x i y i d i 2 1 100 50 1. 5 1 0. 5 0. 25 2 100 1. 5 3 -1. 5 2. 25 3 200 95 3 2 1 1 4 300 225 4 4 0 0 5 400 280 6 6 0 0 6 400 270 6 5 1 1 7 400 340 6 7 -1 1 8 500 380 9. 5 8 1. 5 2. 25 9 500 400 9. 5 9 0. 5 0. 25 10 500 455 9. 5 10 -0. 5 0. 25 11 500 480 9. 5 11 -1. 5 2. 25 12 600 535 12 12 0 0 Total 10. 59633. 0 )112(12 5. 106 1 )1( 6 1 2 2 1 2 nn d r n i i S
STAT 6202 Chapter 2 2012/2013 44 SPEARMAN’s CORRELATION COEFFICIENT An example (3) A HOUSEHOLD SPENDING EXAMPLE Household Rank Obs Income (£) Expenditure (£) x i y i d i 2 1 100 50 1. 5 1 0. 5 0. 25 2 100 1. 5 3 -1. 5 2. 25 3 200 95 3 2 1 1 4 300 225 4 4 0 0 5 400 280 6 6 0 0 6 400 270 6 5 1 1 7 400 340 6 7 -1 1 8 500 380 9. 5 8 1. 5 2. 25 9 500 400 9. 5 9 0. 5 0. 25 10 500 455 9. 5 10 -0. 5 0. 25 11 500 480 9. 5 11 -1. 5 2. 25 12 600 535 12 12 0 0 Total 10. 59633. 0 )112(12 5. 106 1 )1( 6 1 2 2 1 2 nn d r n i i S

