STAT 6202 Chapter 1 2012/2013 1 STAT 6202:



































- Размер: 1.2 Mегабайта
- Количество слайдов: 57
Описание презентации STAT 6202 Chapter 1 2012/2013 1 STAT 6202: по слайдам
 STAT 6202 Chapter 1 2012/2013 1 STAT 6202: Introductory Statistical Methods (B) Dr. Vera Raats Email: vera@stats. ucl. ac. uk Office hours: ? Office: Room 140, 1 -19 Torrington Place Course website: Moodle
STAT 6202 Chapter 1 2012/2013 1 STAT 6202: Introductory Statistical Methods (B) Dr. Vera Raats Email: vera@stats. ucl. ac. uk Office hours: ? Office: Room 140, 1 -19 Torrington Place Course website: Moodle
 STAT 6202 Chapter 1 2012/2013 2 ADMINISTRATION COURSE SET-UP o Weekly lectures: 2 hours o Weekly compulsory tutorials: 1 hour COURSE NOTES AND BOOKS o Print a copy of the course notes yourself o Supplementary reading list (not compulsory) COURSE ASSESSMENT o Two parts ICA (20%): 45 minutes on 14 Nov 2012 Exam (80%): 2. 5 hours in term 3 o Both open book (any printed/written material) and compulsory CALCULATORS: only college approved ones are allowed MOODLE COURSE WEBSITE: enrolment key is Milly
STAT 6202 Chapter 1 2012/2013 2 ADMINISTRATION COURSE SET-UP o Weekly lectures: 2 hours o Weekly compulsory tutorials: 1 hour COURSE NOTES AND BOOKS o Print a copy of the course notes yourself o Supplementary reading list (not compulsory) COURSE ASSESSMENT o Two parts ICA (20%): 45 minutes on 14 Nov 2012 Exam (80%): 2. 5 hours in term 3 o Both open book (any printed/written material) and compulsory CALCULATORS: only college approved ones are allowed MOODLE COURSE WEBSITE: enrolment key is Milly
 STAT 6202 Chapter 1 2012/2013 3 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 3 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
 STAT 6202 Chapter 1 2012/2013 4 POPULATION AND SAMPLES IN A SIMPLE RANDOM SAMPLE EACH INDIVIDUAL IS EQUALLY LIKELY TO GET INTO A SAMPLE. AN EXAMPLE? o The managing director of a large multinational company is interested in the age of managers across her company. o The statistician picks a manager at random from a database of UK managers and calls them. If he cannot make contact he calls another manger (picked at random from the database) until he has information about 20 managers.
STAT 6202 Chapter 1 2012/2013 4 POPULATION AND SAMPLES IN A SIMPLE RANDOM SAMPLE EACH INDIVIDUAL IS EQUALLY LIKELY TO GET INTO A SAMPLE. AN EXAMPLE? o The managing director of a large multinational company is interested in the age of managers across her company. o The statistician picks a manager at random from a database of UK managers and calls them. If he cannot make contact he calls another manger (picked at random from the database) until he has information about 20 managers.
 STAT 6202 Chapter 1 2012/2013 5 POPULATION AND SAMPLES Drawing a simple random sample ASSIGN A UNIQUE NUMBER TO EACH MEMBER OF POPULATION. THEN DRAW RANDOM NUMBERS. o One option: Table 1 o Another (often used) option: Computer randomly generated numbers SAMPLE CONSISTS OF POPULATION MEMBERS WITH (RANDOMLY) SELECTED NUMBERS.
STAT 6202 Chapter 1 2012/2013 5 POPULATION AND SAMPLES Drawing a simple random sample ASSIGN A UNIQUE NUMBER TO EACH MEMBER OF POPULATION. THEN DRAW RANDOM NUMBERS. o One option: Table 1 o Another (often used) option: Computer randomly generated numbers SAMPLE CONSISTS OF POPULATION MEMBERS WITH (RANDOMLY) SELECTED NUMBERS.
 STAT 6202 Chapter 1 2012/2013 6 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 6 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
 STAT 6202 Chapter 1 2012/2013 7 TYPES OF VARIABLES Categorical · hair color (nominal) · smoking status Qualitative Ordinal · degree class (ordered categorical) · severity of illness Discrete · no. of children in family (count) · no. accidents in a week Quantitative Continuous · weight (measurements) · time
STAT 6202 Chapter 1 2012/2013 7 TYPES OF VARIABLES Categorical · hair color (nominal) · smoking status Qualitative Ordinal · degree class (ordered categorical) · severity of illness Discrete · no. of children in family (count) · no. accidents in a week Quantitative Continuous · weight (measurements) · time
 STAT 6202 Chapter 1 2012/2013 8 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 8 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
 STAT 6202 Chapter 1 2012/2013 9 SUMMARY STATISTICS Overview LOCATION: o Mean o Median o Quartiles SPREAD: o Range (min, max) o Interquartile range (IQR) o Variance Or equivalently: standard deviation
STAT 6202 Chapter 1 2012/2013 9 SUMMARY STATISTICS Overview LOCATION: o Mean o Median o Quartiles SPREAD: o Range (min, max) o Interquartile range (IQR) o Variance Or equivalently: standard deviation
 STAT 6202 Chapter 1 2012/2013 10 SUMMARY STATISTICS Notation NOTATION: o Sample size: n o Data values: x 1 , x 2 , … , x n AN EXAMPLE: o Score data: 48 0 87 15 86 55 78 32 60 79 0 65 48 52 7 1 71 59 61 39 62 42 68 77 25 52 29 79 40 82 84 22 0 88 o Number of scores: n =34 o x 1 = 48, x 2 =0, … , x 34 =
STAT 6202 Chapter 1 2012/2013 10 SUMMARY STATISTICS Notation NOTATION: o Sample size: n o Data values: x 1 , x 2 , … , x n AN EXAMPLE: o Score data: 48 0 87 15 86 55 78 32 60 79 0 65 48 52 7 1 71 59 61 39 62 42 68 77 25 52 29 79 40 82 84 22 0 88 o Number of scores: n =34 o x 1 = 48, x 2 =0, … , x 34 =
 STAT 6202 Chapter 1 2012/2013 11 SUMMARY STATISTICS Measures of location: mean MEAN VALUE: SCORE DATA EXAMPLE: o n =34 o Mean: n x n xxx sizesample valuesdataofsum x in i i n 121. . . 68. 53 341825 34 88. . . 048 34. . . 3421 xxx n x x i
STAT 6202 Chapter 1 2012/2013 11 SUMMARY STATISTICS Measures of location: mean MEAN VALUE: SCORE DATA EXAMPLE: o n =34 o Mean: n x n xxx sizesample valuesdataofsum x in i i n 121. . . 68. 53 341825 34 88. . . 048 34. . . 3421 xxx n x x i
 STAT 6202 Chapter 1 2012/2013 12 SUMMARY STATISTICS Measures of location: median MEDIAN: o “ middle” observation o Calculations: (i) Put observations in increasing order (ii) If n is odd: median is value of th observation ( i i i) If n is even: median is average value of th and ( +1 ) th observations 2 1 n 2 n SCORE DATA EXAMPLE: 0 0 0 15 22 25 29 32 39 40 42 48 52 52 55 59 60 61 62 65 68 71 77 78 79 79 82 84 86 87 88 o 34 scores ( n=34 ) o Since n is even, median is the average value of the 17 th and 18 th observations, so median = (59+59)/2=
STAT 6202 Chapter 1 2012/2013 12 SUMMARY STATISTICS Measures of location: median MEDIAN: o “ middle” observation o Calculations: (i) Put observations in increasing order (ii) If n is odd: median is value of th observation ( i i i) If n is even: median is average value of th and ( +1 ) th observations 2 1 n 2 n SCORE DATA EXAMPLE: 0 0 0 15 22 25 29 32 39 40 42 48 52 52 55 59 60 61 62 65 68 71 77 78 79 79 82 84 86 87 88 o 34 scores ( n=34 ) o Since n is even, median is the average value of the 17 th and 18 th observations, so median = (59+59)/2=
 STAT 6202 Chapter 1 2012/2013 13 SUMMARY STATISTICS Measures of location: quartiles QUARTILES: o Lower quartile: q L = v alue that ¼ of data points are less than o Upper quartile: q U = v alue that ¾ of data points are less than o The lower and upper quartiles are also called 25 and 75 percentiles o Calculations: (i) Put data values in increasing order (ii) If n/4 is not a whole number: — q L is j th value, where j is the next integer larger than n/4 — q U is k th value, where k is the next integer larger than 3 n/4 (iii) If n/4 is a whole number: — q L is the average of th and ( +1)th values — q U is the average of th and ( +1)th value s 4 n 4 n 4 3 n
STAT 6202 Chapter 1 2012/2013 13 SUMMARY STATISTICS Measures of location: quartiles QUARTILES: o Lower quartile: q L = v alue that ¼ of data points are less than o Upper quartile: q U = v alue that ¾ of data points are less than o The lower and upper quartiles are also called 25 and 75 percentiles o Calculations: (i) Put data values in increasing order (ii) If n/4 is not a whole number: — q L is j th value, where j is the next integer larger than n/4 — q U is k th value, where k is the next integer larger than 3 n/4 (iii) If n/4 is a whole number: — q L is the average of th and ( +1)th values — q U is the average of th and ( +1)th value s 4 n 4 n 4 3 n
 STAT 6202 Chapter 1 2012/2013 14 SUMMARY STATISTICS Measures of spread RANGE: Largest data value – Smallest data value INTERQUARTILE RANGE: IQR = q U — q L o IQR = distance between upper and lower quartile SAMPLE VARIANCE: STANDARD DEVIATION: Square root of variance On calculator: σ n-1 1 1 22 22 n xxxxxx xx nn x x n s n ii ix 1 22 22 12 n xxxxxx ss n xx
STAT 6202 Chapter 1 2012/2013 14 SUMMARY STATISTICS Measures of spread RANGE: Largest data value – Smallest data value INTERQUARTILE RANGE: IQR = q U — q L o IQR = distance between upper and lower quartile SAMPLE VARIANCE: STANDARD DEVIATION: Square root of variance On calculator: σ n-1 1 1 22 22 n xxxxxx xx nn x x n s n ii ix 1 22 22 12 n xxxxxx ss n xx
 STAT 6202 Chapter 1 2012/2013 15 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 15 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
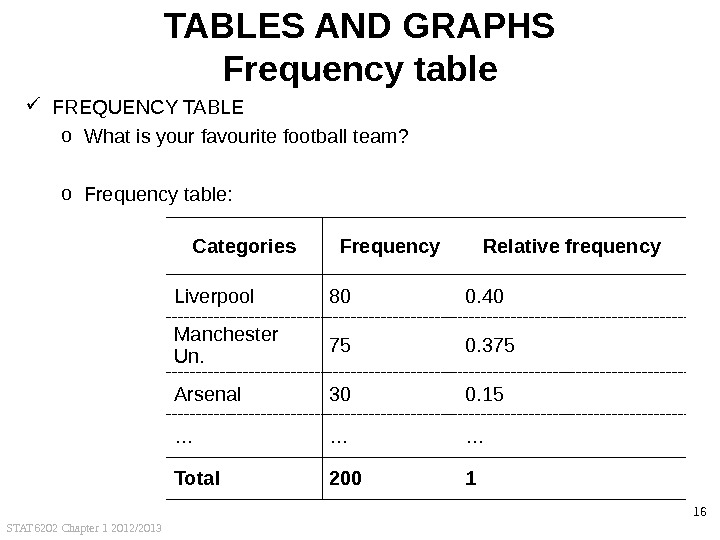
 STAT 6202 Chapter 1 2012/2013 16 TABLES AND GRAPHS Frequency table FREQUENCY TABLE o What is your favourite football team? o Frequency table: Categories Frequency Relative frequency Liverpool 80 0. 40 Manchester Un. 75 0. 375 Arsenal 30 0. 15 … … … Total
STAT 6202 Chapter 1 2012/2013 16 TABLES AND GRAPHS Frequency table FREQUENCY TABLE o What is your favourite football team? o Frequency table: Categories Frequency Relative frequency Liverpool 80 0. 40 Manchester Un. 75 0. 375 Arsenal 30 0. 15 … … … Total
 STAT 6202 Chapter 1 2012/2013 17 TABLES AND GRAPHS A graph overview DISPLAYS OF VARIABLES: Type of variable Graph Qualitative Bar plot Discrete Relative frequency chart (+ below) Continuous Dot plot Stem plot Histogram Box plot
STAT 6202 Chapter 1 2012/2013 17 TABLES AND GRAPHS A graph overview DISPLAYS OF VARIABLES: Type of variable Graph Qualitative Bar plot Discrete Relative frequency chart (+ below) Continuous Dot plot Stem plot Histogram Box plot
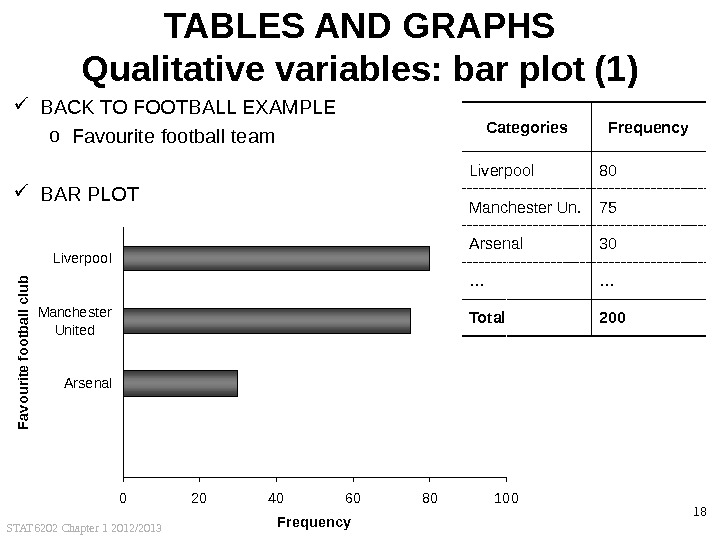
 STAT 6202 Chapter 1 2012/2013 18 TABLES AND GRAPHS Qualitative variables: bar plot (1) BACK TO FOOTBALL EXAMPLE o Favourite football team BAR PLOT Categories Frequency Liverpool 80 Manchester Un. 75 Arsenal 30 … … Total 200 0 20 40 60 80 100 Arsenal. Manchester United. Liverpool. Favourite football club Frequency
STAT 6202 Chapter 1 2012/2013 18 TABLES AND GRAPHS Qualitative variables: bar plot (1) BACK TO FOOTBALL EXAMPLE o Favourite football team BAR PLOT Categories Frequency Liverpool 80 Manchester Un. 75 Arsenal 30 … … Total 200 0 20 40 60 80 100 Arsenal. Manchester United. Liverpool. Favourite football club Frequency
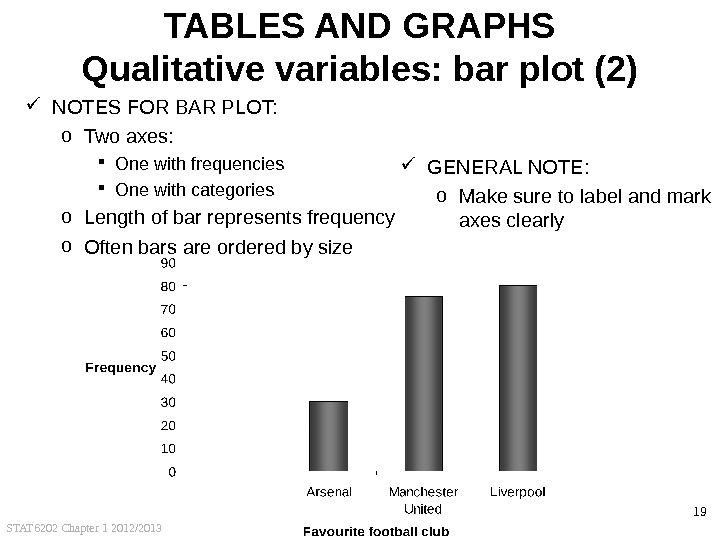
 STAT 6202 Chapter 1 2012/2013 19 TABLES AND GRAPHS Qualitative variables: bar plot (2) NOTES FOR BAR PLOT: o Two axes: One with frequencies One with categories o Length of bar represents frequency o Often bars are ordered by size GENERAL NOTE: o Make sure to label and mark axes clearly
STAT 6202 Chapter 1 2012/2013 19 TABLES AND GRAPHS Qualitative variables: bar plot (2) NOTES FOR BAR PLOT: o Two axes: One with frequencies One with categories o Length of bar represents frequency o Often bars are ordered by size GENERAL NOTE: o Make sure to label and mark axes clearly
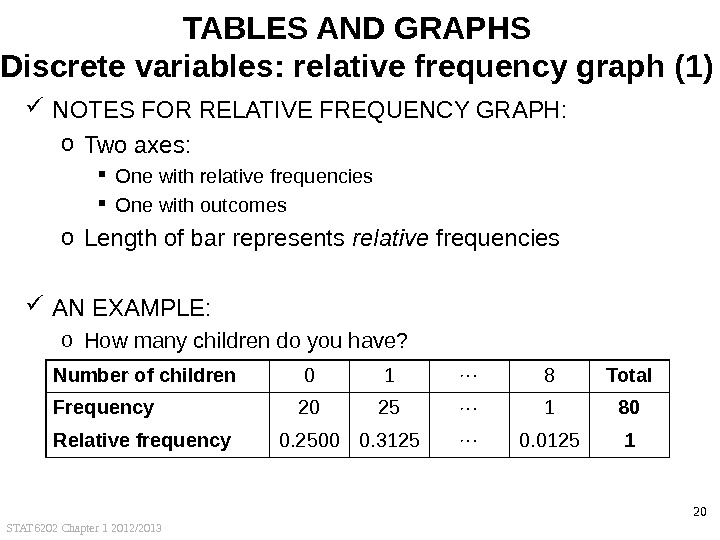
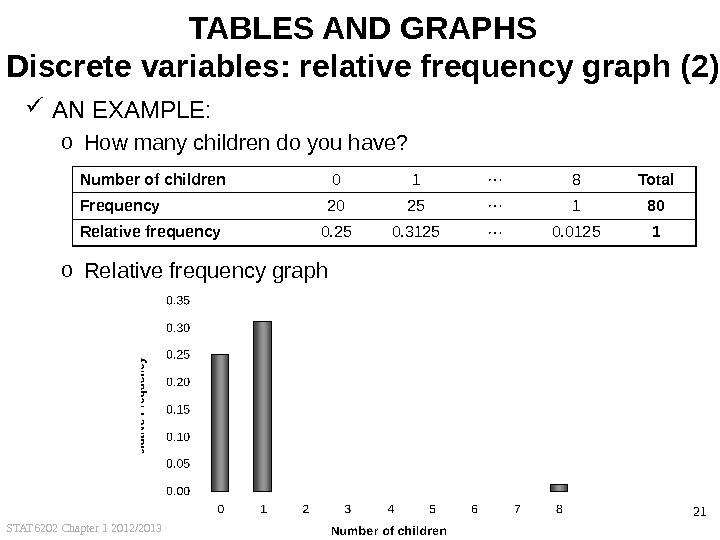
 STAT 6202 Chapter 1 2012/2013 20 TABLES AND GRAPHS Discrete variables: relative frequency graph (1) NOTES FOR RELATIVE FREQUENCY GRAPH: o Two axes: One with relative frequencies One with outcomes o Length of bar represents relative frequencies AN EXAMPLE: o How many children do you have? Number of children 0 1 8 Total Frequency 20 25 1 80 Relative frequency 0. 2500 0. 3125 0.
STAT 6202 Chapter 1 2012/2013 20 TABLES AND GRAPHS Discrete variables: relative frequency graph (1) NOTES FOR RELATIVE FREQUENCY GRAPH: o Two axes: One with relative frequencies One with outcomes o Length of bar represents relative frequencies AN EXAMPLE: o How many children do you have? Number of children 0 1 8 Total Frequency 20 25 1 80 Relative frequency 0. 2500 0. 3125 0.
 STAT 6202 Chapter 1 2012/2013 21 TABLES AND GRAPHS Discrete variables: relative frequency graph (2) AN EXAMPLE: o How many children do you have? o Relative frequency graph. Number of children 0 1 8 Total Frequency 20 25 1 80 Relative frequency 0. 25 0. 3125 0.
STAT 6202 Chapter 1 2012/2013 21 TABLES AND GRAPHS Discrete variables: relative frequency graph (2) AN EXAMPLE: o How many children do you have? o Relative frequency graph. Number of children 0 1 8 Total Frequency 20 25 1 80 Relative frequency 0. 25 0. 3125 0.
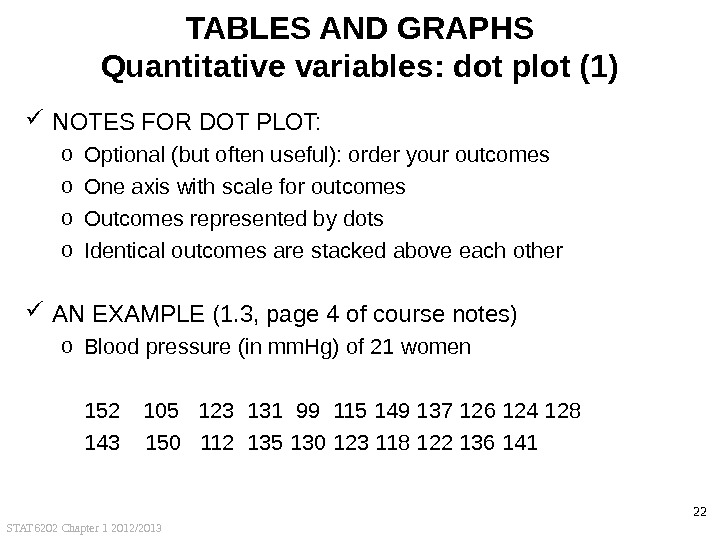
 STAT 6202 Chapter 1 2012/2013 22 TABLES AND GRAPHS Quantitative variables: dot plot (1) NOTES FOR DOT PLOT: o Optional (but often useful): order your outcomes o One axis with scale for outcomes o Outcomes represented by dots o Identical outcomes are stacked above each other AN EXAMPLE (1. 3, page 4 of course notes) o Blood pressure (in mm. Hg) of 21 women
STAT 6202 Chapter 1 2012/2013 22 TABLES AND GRAPHS Quantitative variables: dot plot (1) NOTES FOR DOT PLOT: o Optional (but often useful): order your outcomes o One axis with scale for outcomes o Outcomes represented by dots o Identical outcomes are stacked above each other AN EXAMPLE (1. 3, page 4 of course notes) o Blood pressure (in mm. Hg) of 21 women
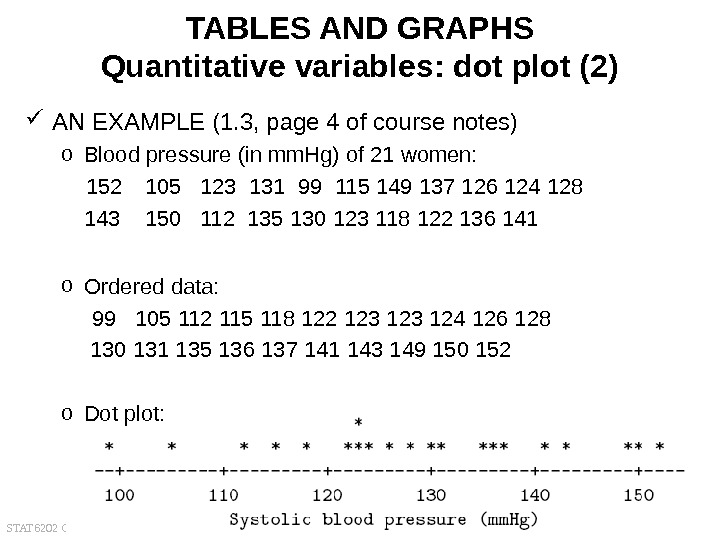
 STAT 6202 Chapter 1 2012/2013 23 TABLES AND GRAPHS Quantitative variables: dot plot (2) AN EXAMPLE (1. 3, page 4 of course notes) o Blood pressure (in mm. Hg) of 21 women: 152 105 123 131 99 115 149 137 126 124 128 143 150 112 135 130 123 118 122 136 141 o Ordered data: 99 105 112 115 118 122 123 124 126 128 130 131 135 136 137 141 143 149 150 152 o Dot plot:
STAT 6202 Chapter 1 2012/2013 23 TABLES AND GRAPHS Quantitative variables: dot plot (2) AN EXAMPLE (1. 3, page 4 of course notes) o Blood pressure (in mm. Hg) of 21 women: 152 105 123 131 99 115 149 137 126 124 128 143 150 112 135 130 123 118 122 136 141 o Ordered data: 99 105 112 115 118 122 123 124 126 128 130 131 135 136 137 141 143 149 150 152 o Dot plot:
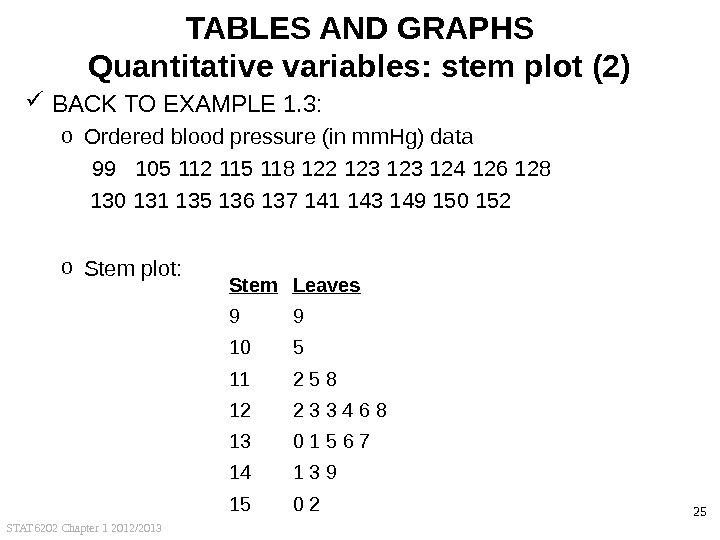
 STAT 6202 Chapter 1 2012/2013 24 TABLES AND GRAPHS Quantitative variables: stem plot (1) NOTES FOR STEM PLOT: o Optional (but often useful): order your outcomes o Often: take the last digit as “leaf”, rest is stem o Usually aim at 5 -15 stem values, otherwise Round values (example on page 5 of course notes) Repeat stem (example in a couple of slides) o Stem plot is less suitable for large amounts of data BACK TO EXAMPLE 1. 3: o Ordered blood pressure (in mm. Hg) data:
STAT 6202 Chapter 1 2012/2013 24 TABLES AND GRAPHS Quantitative variables: stem plot (1) NOTES FOR STEM PLOT: o Optional (but often useful): order your outcomes o Often: take the last digit as “leaf”, rest is stem o Usually aim at 5 -15 stem values, otherwise Round values (example on page 5 of course notes) Repeat stem (example in a couple of slides) o Stem plot is less suitable for large amounts of data BACK TO EXAMPLE 1. 3: o Ordered blood pressure (in mm. Hg) data:
 STAT 6202 Chapter 1 2012/2013 25 TABLES AND GRAPHS Quantitative variables: stem plot (2) BACK TO EXAMPLE 1. 3: o Ordered blood pressure (in mm. Hg) data 99 105 112 115 118 122 123 124 126 128 130 131 135 136 137 141 143 149 150 152 o Stem plot: Stem Leaves
STAT 6202 Chapter 1 2012/2013 25 TABLES AND GRAPHS Quantitative variables: stem plot (2) BACK TO EXAMPLE 1. 3: o Ordered blood pressure (in mm. Hg) data 99 105 112 115 118 122 123 124 126 128 130 131 135 136 137 141 143 149 150 152 o Stem plot: Stem Leaves
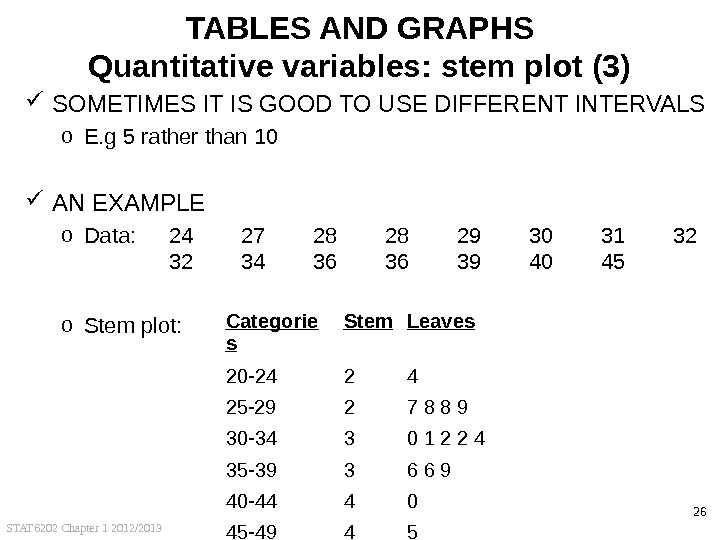
 STAT 6202 Chapter 1 2012/2013 26 TABLES AND GRAPHS Quantitative variables: stem plot (3) SOMETIMES IT IS GOOD TO USE DIFFERENT INTERVALS o E. g 5 rather than 10 AN EXAMPLE o Data: 24 27 28 28 29 30 31 32 32 34 36 36 39 40 45 o Stem plot: Categorie s Stem Leaves 20 -24 2 4 25 -29 2 7 8 8 9 30 -34 3 0 1 2 2 4 35 -39 3 6 6 9 40 -44 4 0 45 —
STAT 6202 Chapter 1 2012/2013 26 TABLES AND GRAPHS Quantitative variables: stem plot (3) SOMETIMES IT IS GOOD TO USE DIFFERENT INTERVALS o E. g 5 rather than 10 AN EXAMPLE o Data: 24 27 28 28 29 30 31 32 32 34 36 36 39 40 45 o Stem plot: Categorie s Stem Leaves 20 -24 2 4 25 -29 2 7 8 8 9 30 -34 3 0 1 2 2 4 35 -39 3 6 6 9 40 -44 4 0 45 —
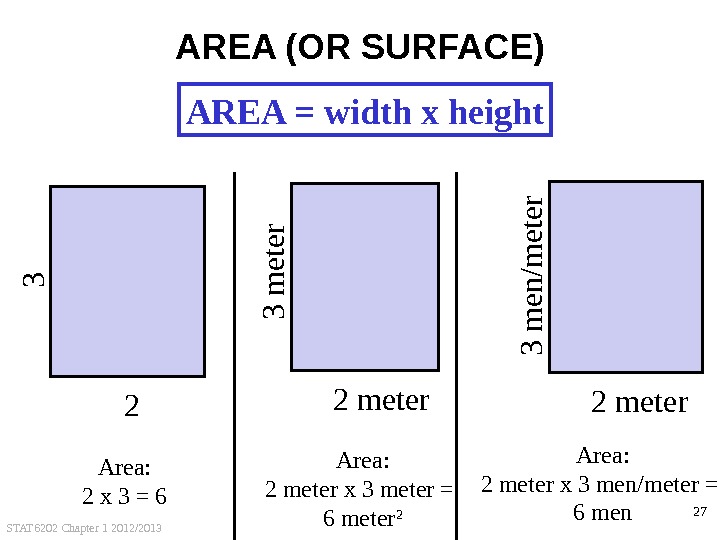
 STAT 6202 Chapter 1 2012/2013 27 AREA (OR SURFACE) 23 Area: 2 x 3 = 6 Area: 2 meter x 3 meter = 6 meter 2 Area: 2 meter x 3 men/meter = 6 men. AREA = width x height 2 meter 3 m e n /m e te r 2 meter 3 m e te r
STAT 6202 Chapter 1 2012/2013 27 AREA (OR SURFACE) 23 Area: 2 x 3 = 6 Area: 2 meter x 3 meter = 6 meter 2 Area: 2 meter x 3 men/meter = 6 men. AREA = width x height 2 meter 3 m e n /m e te r 2 meter 3 m e te r
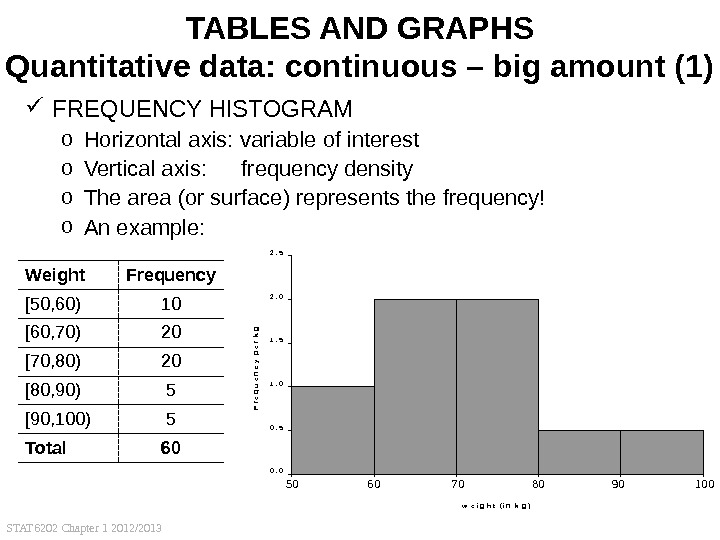
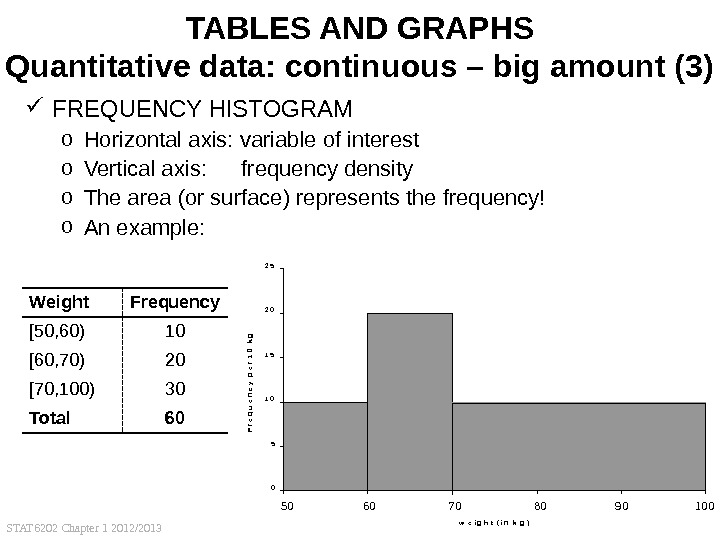
 STAT 6202 Chapter 1 2012/2013 28 TABLES AND GRAPHS Quantitative data: continuous – big amount (1) FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: frequency density o The area (or surface) represents the frequency! o An example: Weight Frequency [50, 60) 10 [60, 70) 20 [70, 80) 20 [80, 90) 5 [90, 100) 5 Total 60 0. 00. 51. 01. 52. 02. 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Frequency per kg 50 60 70 80 90 1000. 51. 01. 52. 02. 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Frequency per kg
STAT 6202 Chapter 1 2012/2013 28 TABLES AND GRAPHS Quantitative data: continuous – big amount (1) FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: frequency density o The area (or surface) represents the frequency! o An example: Weight Frequency [50, 60) 10 [60, 70) 20 [70, 80) 20 [80, 90) 5 [90, 100) 5 Total 60 0. 00. 51. 01. 52. 02. 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Frequency per kg 50 60 70 80 90 1000. 51. 01. 52. 02. 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Frequency per kg
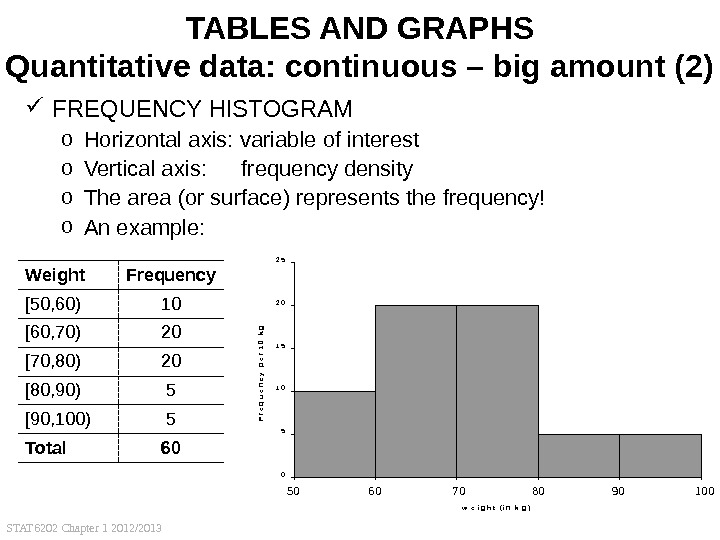
 STAT 6202 Chapter 1 2012/2013 29051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Frequency per 10 kg 50 60 70 80 90 100051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Frequency per 10 kg 50 60 70 80 90 100 TABLES AND GRAPHS Quantitative data: continuous – big amount (2) FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: frequency density o The area (or surface) represents the frequency! o An example: Weight Frequency [50, 60) 10 [60, 70) 20 [70, 80) 20 [80, 90) 5 [90, 100) 5 Total
STAT 6202 Chapter 1 2012/2013 29051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Frequency per 10 kg 50 60 70 80 90 100051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Frequency per 10 kg 50 60 70 80 90 100 TABLES AND GRAPHS Quantitative data: continuous – big amount (2) FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: frequency density o The area (or surface) represents the frequency! o An example: Weight Frequency [50, 60) 10 [60, 70) 20 [70, 80) 20 [80, 90) 5 [90, 100) 5 Total
 STAT 6202 Chapter 1 2012/2013 30 TABLES AND GRAPHS Quantitative data: continuous – big amount (3) FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: frequency density o The area (or surface) represents the frequency! o An example: Weight Frequency [50, 60) 10 [60, 70) 20 [70, 100) 30 Total 60 051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Frequency per 10 kg 50 60 70 80 90 100051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Frequency per 10 kg
STAT 6202 Chapter 1 2012/2013 30 TABLES AND GRAPHS Quantitative data: continuous – big amount (3) FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: frequency density o The area (or surface) represents the frequency! o An example: Weight Frequency [50, 60) 10 [60, 70) 20 [70, 100) 30 Total 60 051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Frequency per 10 kg 50 60 70 80 90 100051 01 52 02 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Frequency per 10 kg
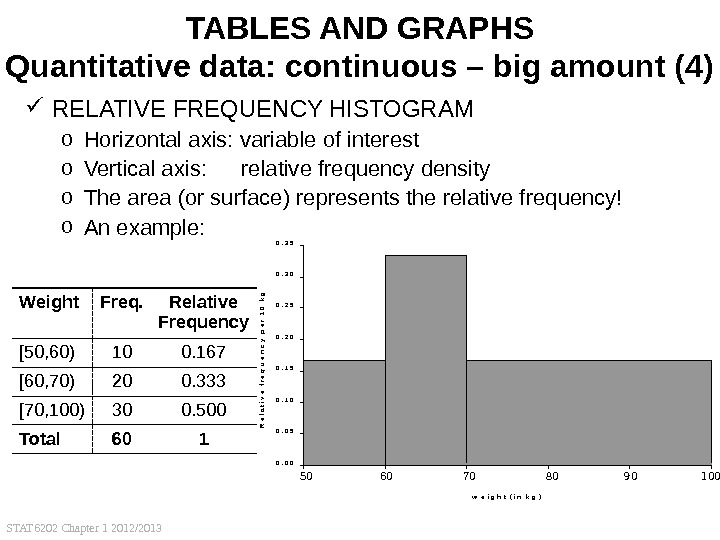
 STAT 6202 Chapter 1 2012/2013 310. 0 00. 0 50. 1 00. 1 50. 2 00. 2 50. 3 00. 3 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Relative frequency per 10 kg 50 60 70 80 90 1000. 0 50. 1 00. 1 50. 2 00. 2 50. 3 00. 3 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Relative frequency per 10 kg 50 60 70 80 90 100 TABLES AND GRAPHS Quantitative data: continuous – big amount (4) RELATIVE FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: relative frequency density o The area (or surface) represents the relative frequency! o An example: Weight Freq. Relative Frequency [50, 60) 10 0. 167 [60, 70) 20 0. 333 [70, 100) 30 0. 500 Total
STAT 6202 Chapter 1 2012/2013 310. 0 00. 0 50. 1 00. 1 50. 2 00. 2 50. 3 00. 3 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g )Relative frequency per 10 kg 50 60 70 80 90 1000. 0 50. 1 00. 1 50. 2 00. 2 50. 3 00. 3 5 5 0 — 6 0 — 7 0 — 8 0 — 9 0 — 1 0 0 w e i g h t ( i n k g ) Relative frequency per 10 kg 50 60 70 80 90 100 TABLES AND GRAPHS Quantitative data: continuous – big amount (4) RELATIVE FREQUENCY HISTOGRAM o Horizontal axis: variable of interest o Vertical axis: relative frequency density o The area (or surface) represents the relative frequency! o An example: Weight Freq. Relative Frequency [50, 60) 10 0. 167 [60, 70) 20 0. 333 [70, 100) 30 0. 500 Total
 STAT 6202 Chapter 1 2012/2013 32 QUIZ 50 people questioned owned 1 computer Frequency histogram How many people owned 2 or 3 computers? (a) 50 (b) 100 (c)
STAT 6202 Chapter 1 2012/2013 32 QUIZ 50 people questioned owned 1 computer Frequency histogram How many people owned 2 or 3 computers? (a) 50 (b) 100 (c)
 STAT 6202 Chapter 1 2012/2013 33 TABLES AND GRAPHS Quantitative variables: histogram (5) EXAMPLE CONTINUED: o Relative frequency histogram
STAT 6202 Chapter 1 2012/2013 33 TABLES AND GRAPHS Quantitative variables: histogram (5) EXAMPLE CONTINUED: o Relative frequency histogram
 STAT 6202 Chapter 1 2012/2013 34 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 34 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
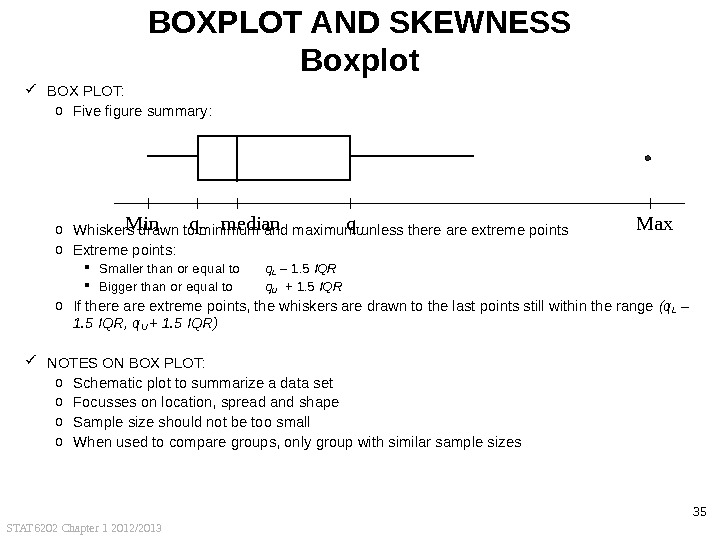
 STAT 6202 Chapter 1 2012/2013 35 BOXPLOT AND SKEWNESS Boxplot BOX PLOT: o Five figure summary: o Whiskers drawn to minimum and maximum unless there are extreme points o Extreme points: Smaller than or equal to q L – 1. 5 IQR Bigger than or equal to q U + 1. 5 IQR o If there are extreme points, the whiskers are drawn to the last points still within the range (q L – 1. 5 IQR, q U + 1. 5 IQR) NOTES ON BOX PLOT: o Schematic plot to summarize a data set o Focusses on location, spread and shape o Sample size should not be too small o When used to compare groups, only group with similar sample sizes Min q L median q U Max
STAT 6202 Chapter 1 2012/2013 35 BOXPLOT AND SKEWNESS Boxplot BOX PLOT: o Five figure summary: o Whiskers drawn to minimum and maximum unless there are extreme points o Extreme points: Smaller than or equal to q L – 1. 5 IQR Bigger than or equal to q U + 1. 5 IQR o If there are extreme points, the whiskers are drawn to the last points still within the range (q L – 1. 5 IQR, q U + 1. 5 IQR) NOTES ON BOX PLOT: o Schematic plot to summarize a data set o Focusses on location, spread and shape o Sample size should not be too small o When used to compare groups, only group with similar sample sizes Min q L median q U Max
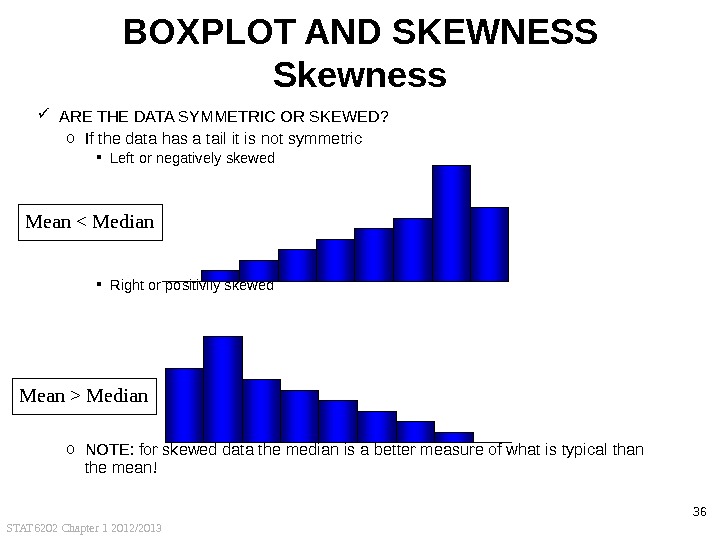
 STAT 6202 Chapter 1 2012/2013 36 BOXPLOT AND SKEWNESS Skewness ARE THE DATA SYMMETRIC OR SKEWED? o If the data has a tail it is not symmetric Left or negatively skewed Right or positivily skewed o NOTE: for skewed data the median is a better measure of what is typical than the mean!Mean Median
STAT 6202 Chapter 1 2012/2013 36 BOXPLOT AND SKEWNESS Skewness ARE THE DATA SYMMETRIC OR SKEWED? o If the data has a tail it is not symmetric Left or negatively skewed Right or positivily skewed o NOTE: for skewed data the median is a better measure of what is typical than the mean!Mean Median
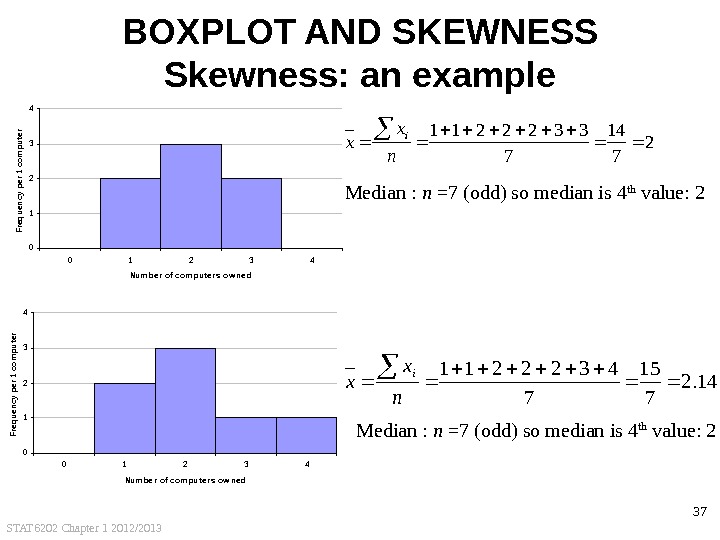
 STAT 6202 Chapter 1 2012/2013 37 BOXPLOT AND SKEWNESS Skewness: an example 2 7 14 7 3322211 n x xi Median : n =7 (odd) so median is 4 th value: 2 14. 2 7 15 7 4322211 n x x i Median : n =7 (odd) so median is 4 th value: 2 01234 0 1 2 3 4 Num be r of com pute r s ow ne d Frequency per 1 computer
STAT 6202 Chapter 1 2012/2013 37 BOXPLOT AND SKEWNESS Skewness: an example 2 7 14 7 3322211 n x xi Median : n =7 (odd) so median is 4 th value: 2 14. 2 7 15 7 4322211 n x x i Median : n =7 (odd) so median is 4 th value: 2 01234 0 1 2 3 4 Num be r of com pute r s ow ne d Frequency per 1 computer
 STAT 6202 Chapter 1 2012/2013 38 DESCRIPTIVE STATISTICS What are we trying to do? DETECT MAIN DATA FEATURES AND PATTERNS o Location, spread, shape o Exception to the general pattern, e. g. outliers o Comparison between groups (see appendix) o Relationships between variables SUMMARIZE THE ESSENTIAL INFORMATION o Often combination of text, summary statistics and graphs best PRESENT RESULTS INFORMATIVELY AND WITH INTEGRITY SEE THROUGH INADEQUATE AND MISLEADING PRESENTATION
STAT 6202 Chapter 1 2012/2013 38 DESCRIPTIVE STATISTICS What are we trying to do? DETECT MAIN DATA FEATURES AND PATTERNS o Location, spread, shape o Exception to the general pattern, e. g. outliers o Comparison between groups (see appendix) o Relationships between variables SUMMARIZE THE ESSENTIAL INFORMATION o Often combination of text, summary statistics and graphs best PRESENT RESULTS INFORMATIVELY AND WITH INTEGRITY SEE THROUGH INADEQUATE AND MISLEADING PRESENTATION
 STAT 6202 Chapter 1 2012/2013 39 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 39 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
 STAT 6202 Chapter 1 2012/2013 40 LINEAR TRANSFORMATIONS The theory SAY WE HAVE DATA xi WITH MEAN AND VARIANCE LINEAR TRANSFORMATIONS OF x i : ui = a + bxi WHAT ARE THE MEAN AND VARIANCE OF u i ? x 2 xs xu xu sbs xbau
STAT 6202 Chapter 1 2012/2013 40 LINEAR TRANSFORMATIONS The theory SAY WE HAVE DATA xi WITH MEAN AND VARIANCE LINEAR TRANSFORMATIONS OF x i : ui = a + bxi WHAT ARE THE MEAN AND VARIANCE OF u i ? x 2 xs xu xu sbs xbau
 STAT 6202 Chapter 1 2012/2013 41 COURSE MARKS (2) SOME SUMMARY STATISTICS: o Number of marks: 177 o Mean mark: 56. 85 o Median mark: 59 o Lowest mark: 11 o Highest mark: 89 o Standard deviation: 17. 99 o Variance: 323.
STAT 6202 Chapter 1 2012/2013 41 COURSE MARKS (2) SOME SUMMARY STATISTICS: o Number of marks: 177 o Mean mark: 56. 85 o Median mark: 59 o Lowest mark: 11 o Highest mark: 89 o Standard deviation: 17. 99 o Variance: 323.
 STAT 6202 Chapter 1 2012/2013 42 LINEAR TRANSFORMATIONS An example: the course marks TO RESCALE THREE OPTIONS ARE CONSIDERED 1. Give everyone 5 marks extra 2. Give everyone 5% of their marks extra 3. Give everyone 5% of their marks extra and then add 5 marks MEAN AND VARIANCE OF RESCALED MARKS 1. ui = 5 + 1 • xi 2. u i = 0 + 1. 05 • xi 3. u i = 5 + 1. 05 • xi 89. 18, 88. 356, 69. 64 89. 18, 88. 356, 69. 59 99. 17, 70. 323, 85. 61 2 2 2 uu uu uu ssu ssu
STAT 6202 Chapter 1 2012/2013 42 LINEAR TRANSFORMATIONS An example: the course marks TO RESCALE THREE OPTIONS ARE CONSIDERED 1. Give everyone 5 marks extra 2. Give everyone 5% of their marks extra 3. Give everyone 5% of their marks extra and then add 5 marks MEAN AND VARIANCE OF RESCALED MARKS 1. ui = 5 + 1 • xi 2. u i = 0 + 1. 05 • xi 3. u i = 5 + 1. 05 • xi 89. 18, 88. 356, 69. 64 89. 18, 88. 356, 69. 59 99. 17, 70. 323, 85. 61 2 2 2 uu uu uu ssu ssu
 STAT 6202 Chapter 1 2012/2013 43 LINEAR TRANSFORMATIONS Standardisation F OR A SAMPLE x 1 , x 2 , …, x n , LET THEN WE HAVE HENCE z 1 , z 2 , …, z n IS CALLED THE STANDARDISED SAMPLE o A nd this process is called standardisation x i xx i i s x x ss xx z 1 1 0 1 x x z xx s s x x s z
STAT 6202 Chapter 1 2012/2013 43 LINEAR TRANSFORMATIONS Standardisation F OR A SAMPLE x 1 , x 2 , …, x n , LET THEN WE HAVE HENCE z 1 , z 2 , …, z n IS CALLED THE STANDARDISED SAMPLE o A nd this process is called standardisation x i xx i i s x x ss xx z 1 1 0 1 x x z xx s s x x s z
 STAT 6202 Chapter 1 2012/2013 44 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
STAT 6202 Chapter 1 2012/2013 44 CHAPTER 1 Data summary and presentation POPULATION AND SAMPLES TYPES OF VARIABLES SUMMARY STATISTICS TABLES AND GRAPHS BOXPLOT AND SKEWNESS LINEAR TRANSFORMATIONS LOG TRANSFORMATIONS
 STAT 6202 Chapter 1 2012/2013 45 LOG TRANSFORMATIONS The log function: what is it? THE INVERSE FUNCTION OF “POWER” FUNCTION A “ 10” EXAMPLE o 1 0 2 = 100 o log 10 (100) = 2 In general o a y = x o log a ( x ) = y Natural logs o e ≈ 2. 7182845905 o e y = x o log e (x) = y log e (x)= log e (10) · log 10 (x) =2. 3026· log 10 (x)
STAT 6202 Chapter 1 2012/2013 45 LOG TRANSFORMATIONS The log function: what is it? THE INVERSE FUNCTION OF “POWER” FUNCTION A “ 10” EXAMPLE o 1 0 2 = 100 o log 10 (100) = 2 In general o a y = x o log a ( x ) = y Natural logs o e ≈ 2. 7182845905 o e y = x o log e (x) = y log e (x)= log e (10) · log 10 (x) =2. 3026· log 10 (x)
 STAT 6202 Chapter 1 2012/2013 46 LOG TRANSFORMATIONS The log function: some properties SOME PROPERTIES : o loga (x) only exists for x>0 o log a (x·z)= loga (x)+ loga (z) o equal ratios ↔ equal differences of log a e. g. 91629. 0)30(log)75(log 91629. 0)20(log)50(log 30 75 20 50 ee ee )(log)(logzx z x aaa
STAT 6202 Chapter 1 2012/2013 46 LOG TRANSFORMATIONS The log function: some properties SOME PROPERTIES : o loga (x) only exists for x>0 o log a (x·z)= loga (x)+ loga (z) o equal ratios ↔ equal differences of log a e. g. 91629. 0)30(log)75(log 91629. 0)20(log)50(log 30 75 20 50 ee ee )(log)(logzx z x aaa
 STAT 6202 Chapter 1 2012/2013 47 LOG TRANSFORMATIONS The log function: some approximations APPROXIMATION PROPERTY o Difference between two numbers, as a fraction of their mean, approximately equals difference between their natural logs: o This works well for fractional differences up to 0. 5 20067. 0)90(log)110(log 20. 0 100 90110 10008. 0)95(log)105(log 10. 0 100 95105 ee ee 847. 0)60(log)140(log 80. 0 100 60140 ee
STAT 6202 Chapter 1 2012/2013 47 LOG TRANSFORMATIONS The log function: some approximations APPROXIMATION PROPERTY o Difference between two numbers, as a fraction of their mean, approximately equals difference between their natural logs: o This works well for fractional differences up to 0. 5 20067. 0)90(log)110(log 20. 0 100 90110 10008. 0)95(log)105(log 10. 0 100 95105 ee ee 847. 0)60(log)140(log 80. 0 100 60140 ee
 STAT 6202 Chapter 1 2012/2013 48 SAMPLE x 1 , x 2 , …, x n o All x 1 , x 2 , …, x n need to be larger than 0 o Transformation results in sample of natural logarithms: log e (x 1 ), log e (x 2 ), …, log e (x n ) HOWEVER, PLEASE NOTE o Mean of log e (x) ≠ log e (mean of x) o S tandard deviation of log e (x) is approximately equal to standard deviation of x divided by the mean of x (this works well for relative standard deviations up to about 0. 5) LOG TRANSFORMATIONS Note for transforming data )( )( ))((log xmean xsd e 2 )( )( 21 ))(log())((log xmean xsd xmean e
STAT 6202 Chapter 1 2012/2013 48 SAMPLE x 1 , x 2 , …, x n o All x 1 , x 2 , …, x n need to be larger than 0 o Transformation results in sample of natural logarithms: log e (x 1 ), log e (x 2 ), …, log e (x n ) HOWEVER, PLEASE NOTE o Mean of log e (x) ≠ log e (mean of x) o S tandard deviation of log e (x) is approximately equal to standard deviation of x divided by the mean of x (this works well for relative standard deviations up to about 0. 5) LOG TRANSFORMATIONS Note for transforming data )( )( ))((log xmean xsd e 2 )( )( 21 ))(log())((log xmean xsd xmean e
 STAT 6202 Chapter 1 2012/2013 49 APPENDIX Comparing groups back
STAT 6202 Chapter 1 2012/2013 49 APPENDIX Comparing groups back
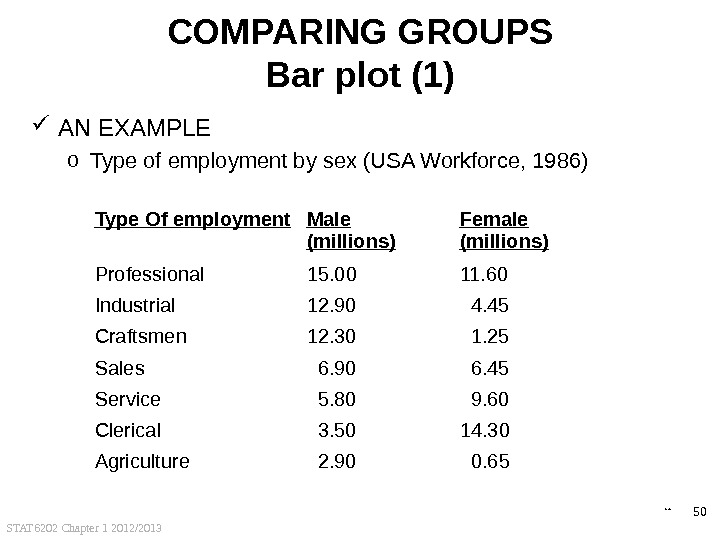
 STAT 6202 Chapter 1 2012/2013 50 COMPARING GROUPS Bar plot (1) AN EXAMPLE o Type of employment by sex (USA Workforce, 1986) Type Of employment Male (millions) Female (millions) Professional 15. 00 11. 60 Industrial 12. 90 4. 45 Craftsmen 12. 30 1. 25 Sales 6. 90 6. 45 Service 5. 80 9. 60 Clerical 3. 50 14. 30 Agriculture 2. 90 0. 65 back
STAT 6202 Chapter 1 2012/2013 50 COMPARING GROUPS Bar plot (1) AN EXAMPLE o Type of employment by sex (USA Workforce, 1986) Type Of employment Male (millions) Female (millions) Professional 15. 00 11. 60 Industrial 12. 90 4. 45 Craftsmen 12. 30 1. 25 Sales 6. 90 6. 45 Service 5. 80 9. 60 Clerical 3. 50 14. 30 Agriculture 2. 90 0. 65 back
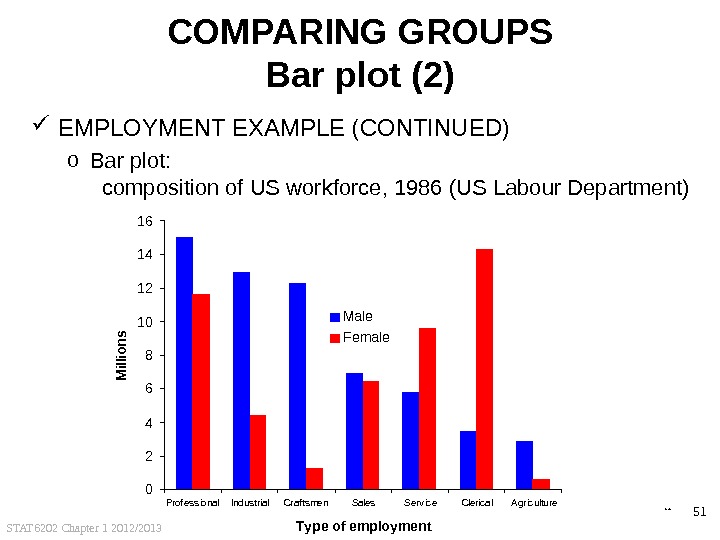
 STAT 6202 Chapter 1 2012/2013 51 COMPARING GROUPS Bar plot (2) EMPLOYMENT EXAMPLE (CONTINUED) o Bar plot: composition of US workforce, 1986 (US Labour Department) 0246810121416 Prof essional Industrial Craf tsmen Sales Service Clerical A griculture Type of employment. M illions Male Female back
STAT 6202 Chapter 1 2012/2013 51 COMPARING GROUPS Bar plot (2) EMPLOYMENT EXAMPLE (CONTINUED) o Bar plot: composition of US workforce, 1986 (US Labour Department) 0246810121416 Prof essional Industrial Craf tsmen Sales Service Clerical A griculture Type of employment. M illions Male Female back
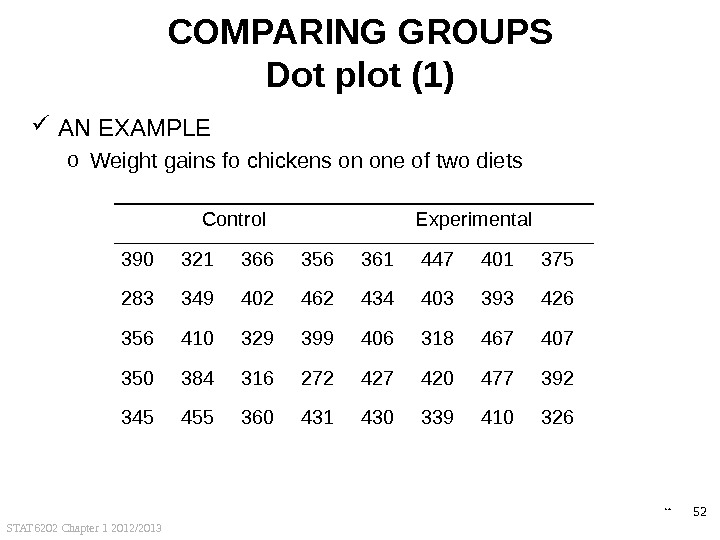
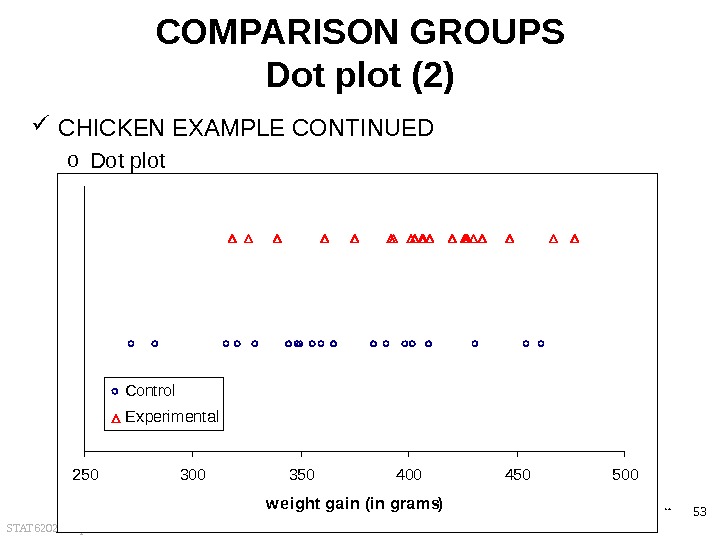
 STAT 6202 Chapter 1 2012/2013 52 COMPARING GROUPS Dot plot (1) AN EXAMPLE o Weight gains fo chickens on one of two diets Control Experimental 390 321 366 356 361 447 401 375 283 349 402 462 434 403 393 426 356 410 329 399 406 318 467 407 350 384 316 272 427 420 477 392 345 455 360 431 430 339 410 326 back
STAT 6202 Chapter 1 2012/2013 52 COMPARING GROUPS Dot plot (1) AN EXAMPLE o Weight gains fo chickens on one of two diets Control Experimental 390 321 366 356 361 447 401 375 283 349 402 462 434 403 393 426 356 410 329 399 406 318 467 407 350 384 316 272 427 420 477 392 345 455 360 431 430 339 410 326 back
 STAT 6202 Chapter 1 2012/2013 53 COMPARISON GROUPS Dot plot (2) CHICKEN EXAMPLE CONTINUED o Dot plot 250 300 350 400 450 500 w e ight ga in (in gra ms)Control Experimental back
STAT 6202 Chapter 1 2012/2013 53 COMPARISON GROUPS Dot plot (2) CHICKEN EXAMPLE CONTINUED o Dot plot 250 300 350 400 450 500 w e ight ga in (in gra ms)Control Experimental back
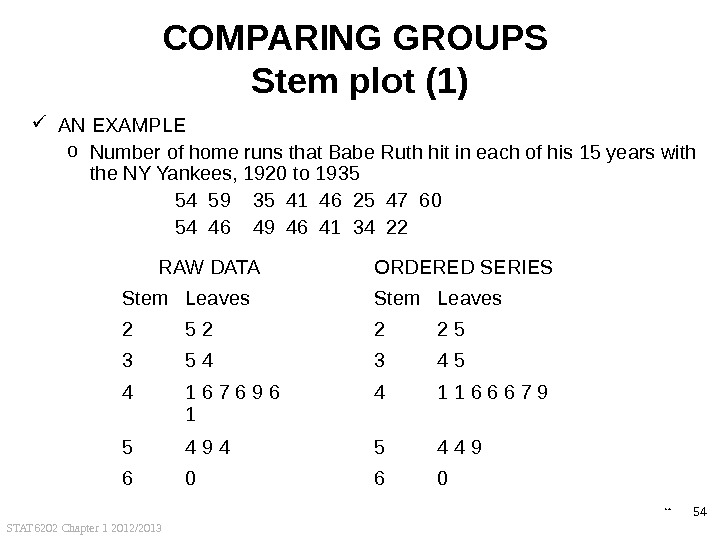
 STAT 6202 Chapter 1 2012/2013 54 COMPARING GROUPS Stem plot (1) AN EXAMPLE o Number of home runs that Babe Ruth hit in each of his 15 years with the NY Yankees, 1920 to 1935 54 59 35 41 46 25 47 60 54 46 49 46 41 34 22 RAW DATA ORDERED SERIES Stem Leaves 2 5 2 2 2 5 3 5 4 3 4 5 4 1 6 7 6 9 6 1 4 1 1 6 6 6 7 9 5 4 9 4 5 4 4 9 6 0 back
STAT 6202 Chapter 1 2012/2013 54 COMPARING GROUPS Stem plot (1) AN EXAMPLE o Number of home runs that Babe Ruth hit in each of his 15 years with the NY Yankees, 1920 to 1935 54 59 35 41 46 25 47 60 54 46 49 46 41 34 22 RAW DATA ORDERED SERIES Stem Leaves 2 5 2 2 2 5 3 5 4 3 4 5 4 1 6 7 6 9 6 1 4 1 1 6 6 6 7 9 5 4 9 4 5 4 4 9 6 0 back
 STAT 6202 Chapter 1 2012/2013 55 COMPARING GROUPS Stem plot (2) EXAMPLE CONTINUED o Home run data also given for Roger Marris: o Back to back stem plot: Babe Ruth Roger Marris Stem 0 8 5 2 1 3 4 6 5 2 2 3 6 8 5 4 3 3 9 9 7 6 6 6 1 1 4 9 4 4 5 0 6 6 1 back
STAT 6202 Chapter 1 2012/2013 55 COMPARING GROUPS Stem plot (2) EXAMPLE CONTINUED o Home run data also given for Roger Marris: o Back to back stem plot: Babe Ruth Roger Marris Stem 0 8 5 2 1 3 4 6 5 2 2 3 6 8 5 4 3 3 9 9 7 6 6 6 1 1 4 9 4 4 5 0 6 6 1 back
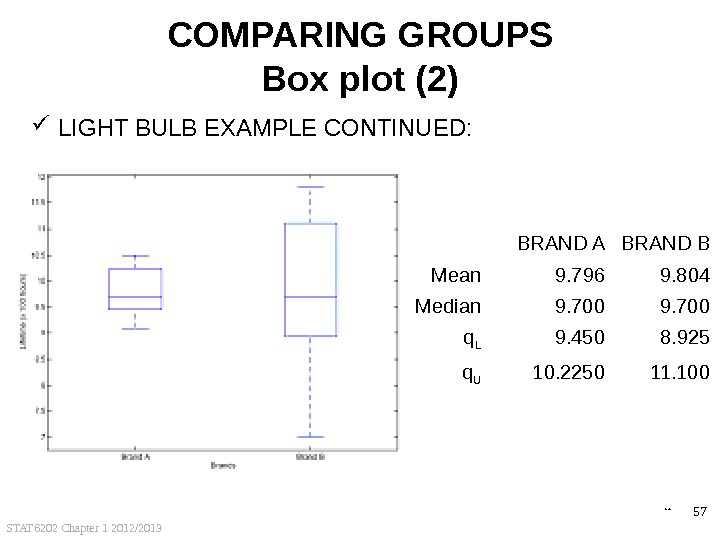
 STAT 6202 Chapter 1 2012/2013 56 COMPARING GROUPS Box plot (1) AN EXAMPLE: Compare lifetime of two light bulb brands (hundreds of hours) o Data: BRAND A BRAND B 10. 500 11. 300 9. 100 7. 000 10. 225 9. 700 10. 000 9. 600 9. 450 10. 500 9. 600 9. 700 11. 800 8. 925 back
STAT 6202 Chapter 1 2012/2013 56 COMPARING GROUPS Box plot (1) AN EXAMPLE: Compare lifetime of two light bulb brands (hundreds of hours) o Data: BRAND A BRAND B 10. 500 11. 300 9. 100 7. 000 10. 225 9. 700 10. 000 9. 600 9. 450 10. 500 9. 600 9. 700 11. 800 8. 925 back
 STAT 6202 Chapter 1 2012/2013 57 COMPARING GROUPS Box plot (2) LIGHT BULB EXAMPLE CONTINUED: BRAND A BRAND B Mean 9. 796 9. 804 Median 9. 700 q L 9. 450 8. 925 q U 10. 2250 11. 100 back
STAT 6202 Chapter 1 2012/2013 57 COMPARING GROUPS Box plot (2) LIGHT BULB EXAMPLE CONTINUED: BRAND A BRAND B Mean 9. 796 9. 804 Median 9. 700 q L 9. 450 8. 925 q U 10. 2250 11. 100 back

