STAGGERED MESH GODUNOV SMG SCHEMES FOR ALE HYDRODYNAMICS

STAGGERED MESH GODUNOV (SMG) SCHEMES FOR ALE HYDRODYNAMICS Gabi Luttwak 1 and Joseph Falcovitz 2 1 Rafael, P. O. Box 2250, Haifa 31021, Israel 2 Institute of Mathematics, The Hebrew University of Jerusalem, Israel

Hydro-Schemes 4 Classical Lagrange (CL) & ALE – staggered in space & time • even schemes are staggered in space with predictor-corrector time integration – pseudo-viscosity used for shock capturing 4 Second Order Godunov (Eulerian) – zone centered variables & gradients – gradients limited to preserve monotonic profiles – Riemann Problems (RP) solved at zone faces 4 We seek the best approach for an MM-ALE code – It is required to treat the flow in both Lagrangian and (Multi-material) Eulerian framework

Staggered Mesh Godunov - SMG schemes: – staggered in space & time • or staggered in space and even-time integration – use RP to capture shocks – bridge the Lagrange-to-Godunov “conceptual gap”

(MM)ALE code 4 Geometry Update (not necessary for pure Euler) – compute areas, volumes etc. 4 Lagrangian Phase – CL/SMG Scheme – Definition of pressure and stress in a MM zone 4 Advection Phase (not present for pure Lagrange) – Second order advection for cell-centered variables – Staggered Mesh Momentum advection • SALE • HIS (Benson) – Single step /Partially-split advected-volume integration – Interface tracking: VOF (Luttwak 1984, 2002) similar to Youngs scheme 4 Grid Motion Algorithm

Classical Lagrange (CL) Schemes 4 simple, efficient and robust – ~ second order accurate for smooth flow • on a uniform mesh with constant time steps – until grid gets distorted 4 pseudo-viscosity is used to capture shocks – over 3 -4 zones – + linear terms required for weak shocks

Pseudo-viscosity 4 form and coefficients somewhat arbitrary – not from first principles 4 unphysical heating in regions of isentropic flow – especially in Multi-D 4 second order Godunov-like methods help overcome deficiencies of classical Lagrange Q – e. g. Christensen, Benson, Caramana et al.

Second-order zone-centered Godunov 4 sharp shock resolution < 2 zone thick 4 second order accurate 4 physically intuitive BUT 4 hard to add more physics – Elastic-plastic flow, chemical reaction etc. 4 Multi-D is well formulated only in Eulerian coordinates (operator splitting)

Zone-Centered Godunov with Lagrange/ALE mesh 4 Vertex velocities obtained by interpolating either – zone-centered velocities (from momentum equation), or – face velocities (from RP solution) 4 Result: Weak coupling between node motion and zone deformation – Spurious grid deformation – Remedy: SMG scheme

SMG schemes 4 SMG/L scheme – RP solved only at zone faces • Zone-centered velocity obtained by interpolation of vertex velocities • Face-centered data extrapolated from the zone-centered data using the (limited) zone–centered gradients – Additional impulse due to RP solution distributed to neighboring vertices 4 SMG/G scheme – “collision” RP solved at corner-zone faces is used to update the momentum equation – “contact discontinuity” RP solved at zone faces serves to update the (total) energy equation 4 SMG/Q scheme (closest to CL)

Staggered Mesh 4 Zone-centered but node-centered velocity 4 velocity jump on corner-zone faces 4 Jump in only at the zone faces – zones k, edge-neighbor nodes i, i+1 – Corner-zones (i, k). – The faces separate corner-zones (i, k) and (i+1, k)

SMG/Q scheme 4 Data for “collision” RP at corner zone faces: – velocity jump at face – Continuous – : in zone k depends on velocity gradient in the zone and on velocity in neighboring nodes. for first order accuracy (sharp velocity jump). in regions of smooth flow. solution

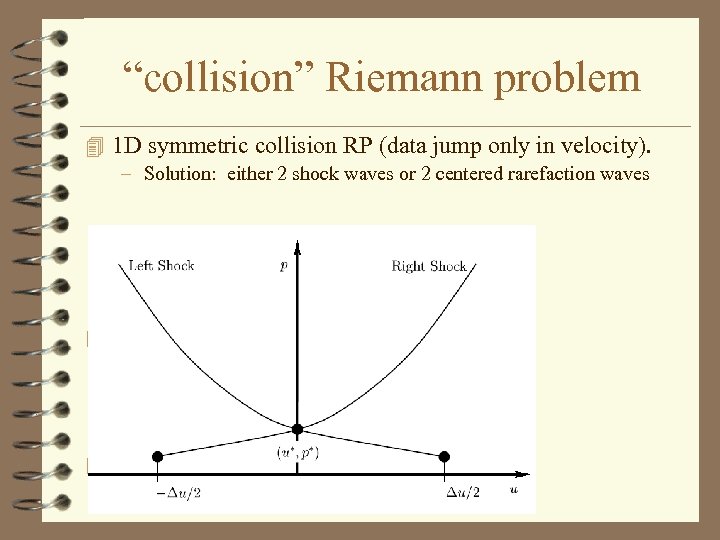“collision” Riemann problem 4 1 D symmetric collision RP (data jump only in velocity). – Solution: either 2 shock waves or 2 centered rarefaction waves 4 4

SMG/Q scheme 4 momentum equation: – sum up “corner face forces” on all faces surrounding node i 4 internal energy equation: – assume all work performed by against the deformation of zone k is deposited in the zone

SMG/Q characteristics 4 As each depends only on the velocity difference the Lagrange scheme is Galilei-Invariant (like CL). 4 As in “traditional” Godunov schemes no pseudo-viscosity is required. 4 Needs solution to a simple “collision” RP. 4 Formulated with internal energy. – see also Christensen, Caramana et al.

SMG/Q and pseudo-viscosity 4 We can regard as a kind of pseudo-viscosity. – as at a shock • except at phase changes or for reacting HE. – define it as a uni-axial tensor acting along the velocity difference (Not along ).

Uni-axial tensor Q 4 Edge-defined Q is better if related lumped forces are aligned with the velocity difference, instead of the edge (Margolin, Caramana et al. ). – a moment opposing edge rotation is thereby generated (a grid stabilizing effect). 4 Summing up “corner face forces” over all faces separating edge-neighbor nodes, produces normal-to-face forces. 4 Alternately define as uni-axial tensor along the direction of :

The Riemann Problem solutions 4 The RP solution is aimed to provide the necessary dissipation at shocks. 4 An approximate Riemann solution may be adequate for moderate shocks. 4 SMG/Q can be used for elastic-plastic and reactive flow even without solving the exact RP (with results at least similar to Q-based CL). – Using the specific RP solution in each case might further improve the results.

“Collision” RP solution 4 The Hugoniot is and the RP can be solved assuming a linear shock-to-particle-velocity relationship 4 The exact RP can be solved numerically (or, for an ideal gas, analytically) at strong shocks or strong rarefactions. 4 Note: two waves, each with half the velocity jump !! 4 Kuropatenko’s Q: single shock with full velocity jump!!

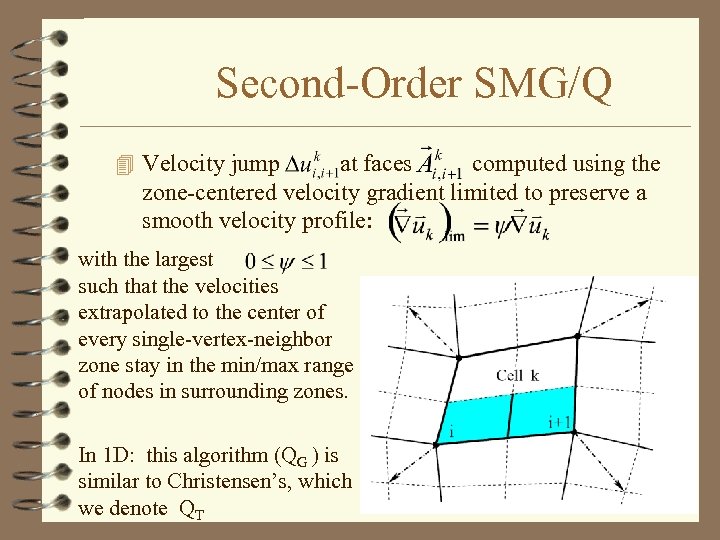Second-Order SMG/Q 4 Velocity jump at faces computed using the zone-centered velocity gradient limited to preserve a smooth velocity profile: with the largest such that the velocities extrapolated to the center of every single-vertex-neighbor zone stay in the min/max range of nodes in surrounding zones. In 1 D: this algorithm (QG ) is similar to Christensen’s, which we denote QT

The slope limiter 4 This limiter extends van Leer 1 D scheme to a multi-D staggered mesh – Uses average zone-centered velocity gradient – The limiter is defined on either structured or unstructured mesh – In 1 D it reduces to , while Christensen’s TVD-like limiter is:

Planar Noh Problem 4 with the data: 4 and analytic solution: 4 The 1 D calculation had 100 unit length zones 4 An exact Rieman solver was used in the 1 D simulations 4 Sharp and accurate shock capture and almost identical results for QG and QT

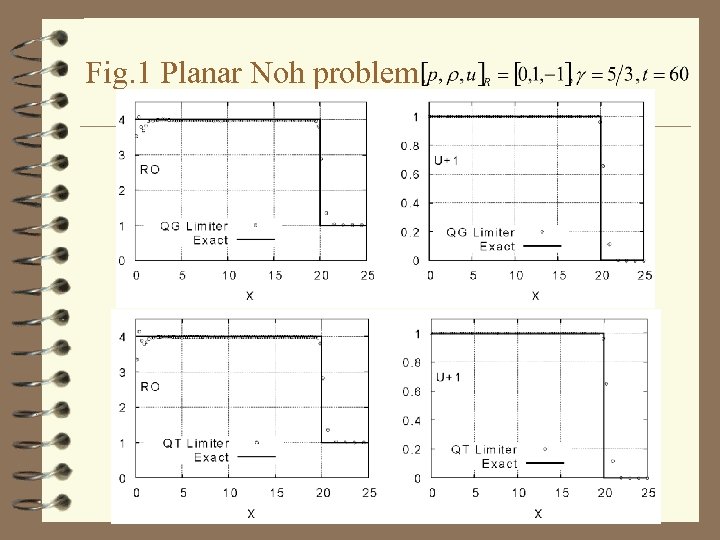Fig. 1 Planar Noh problem.

Centered Compression Wave (CCW) 4 The initial (t=0) smooth profile has steepened up to a sharp discontinuity at t=20 – The t=0 profile is the “inverse” of a centered rarefaction with a linear velocity distribution 4 Results show an almost isentropic compression

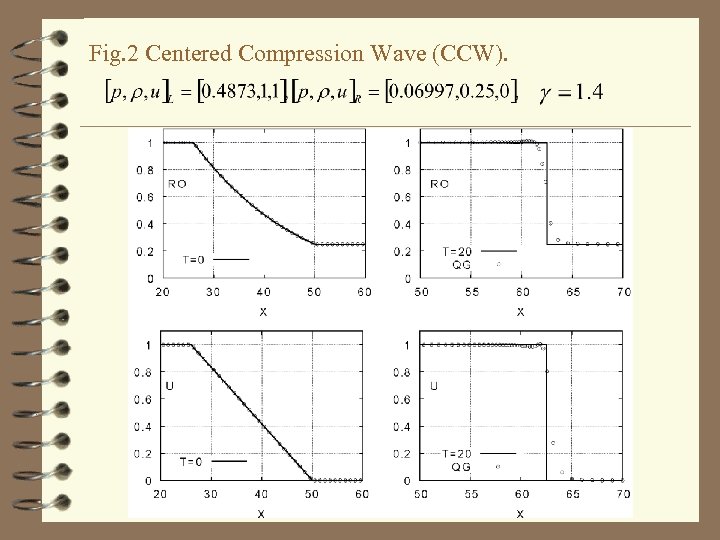Fig. 2 Centered Compression Wave (CCW).

The Sod Problem 4 The initial (shock tube) data: 4 It was run with 100 unit-size zones. 4 The results at t=20 compare favorably to those of the GRP (a genuine second-order Godunov scheme see Ben Artzi & Falcovitz) 4 SMG with even-time integration gave virtually identical results for this problem

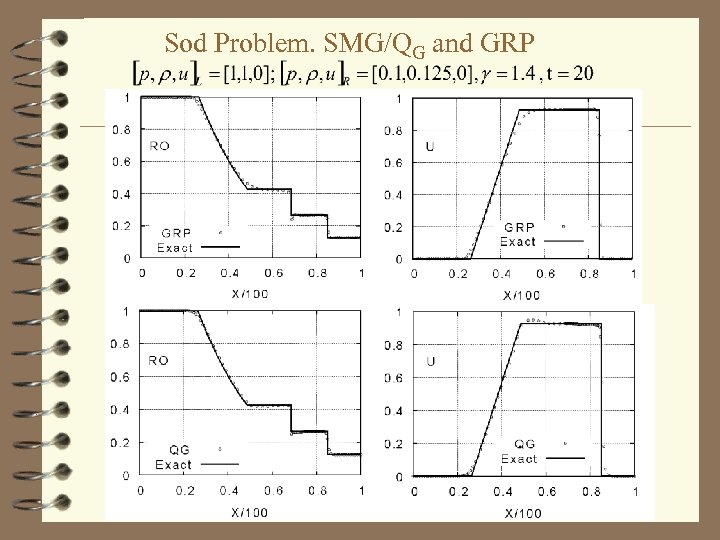Sod Problem. SMG/QG and GRP

Sedov-Taylor blast wave problem 4 The initial data is: ideal gas with a “point source” represented by setting in a single zone at the origin (see Caramana et al. ) 4 The physical space is a 253 box divided into a uniform 903 mesh 4 3 D computation conducted in the octant with the symmetry planes 4 The exact solution has a post-shock density and the front radius is at. cold

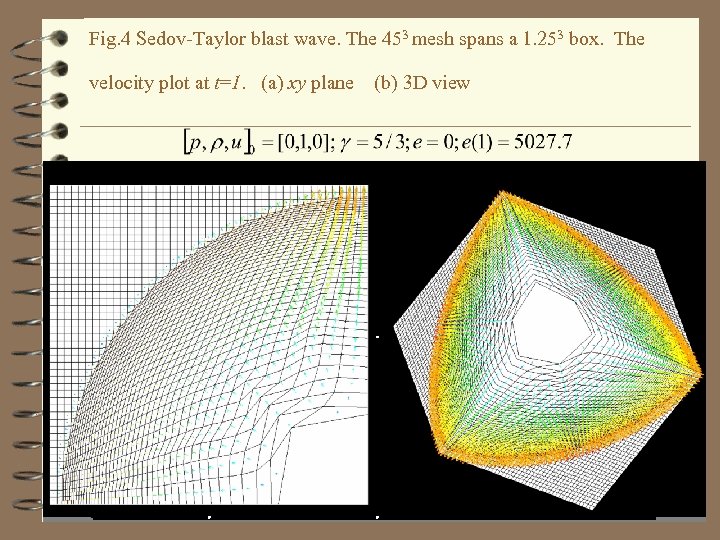Fig. 4 Sedov-Taylor blast wave. The 453 mesh spans a 1. 253 box. The velocity plot at t=1. (a) xy plane (b) 3 D view

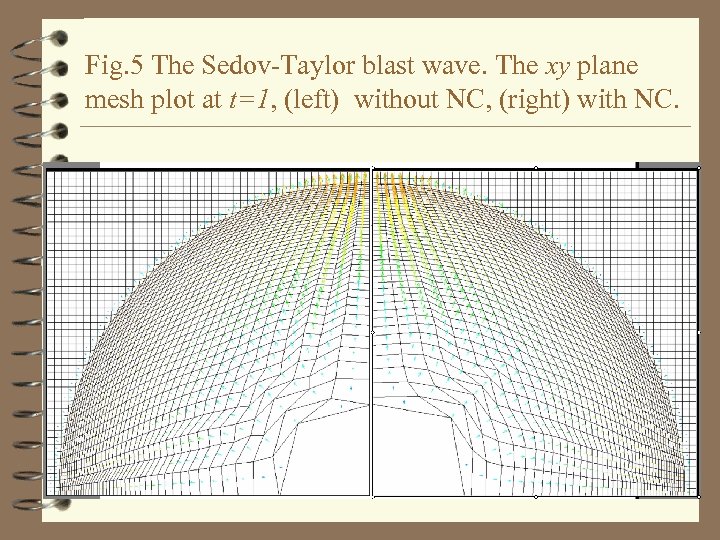Fig. 5 The Sedov-Taylor blast wave. The xy plane mesh plot at t=1, (left) without NC, (right) with NC.

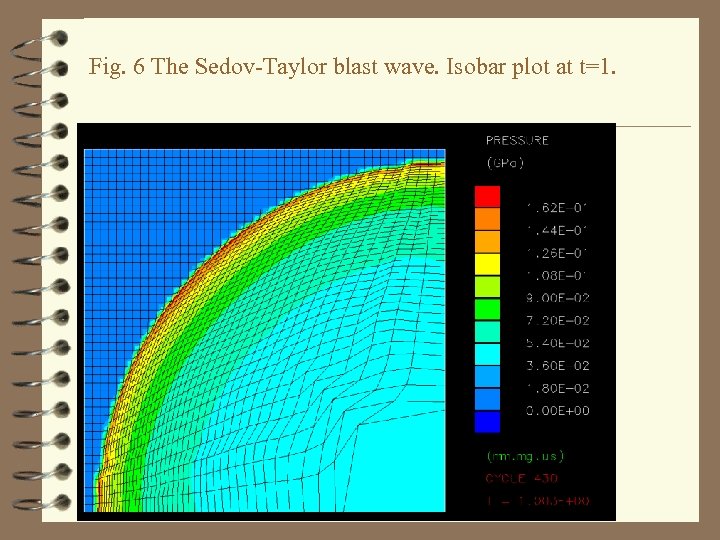Fig. 6 The Sedov-Taylor blast wave. Isobar plot at t=1.

Fig. 7 The Sedov-Taylor blast wave. Isodensity plot at t=1.

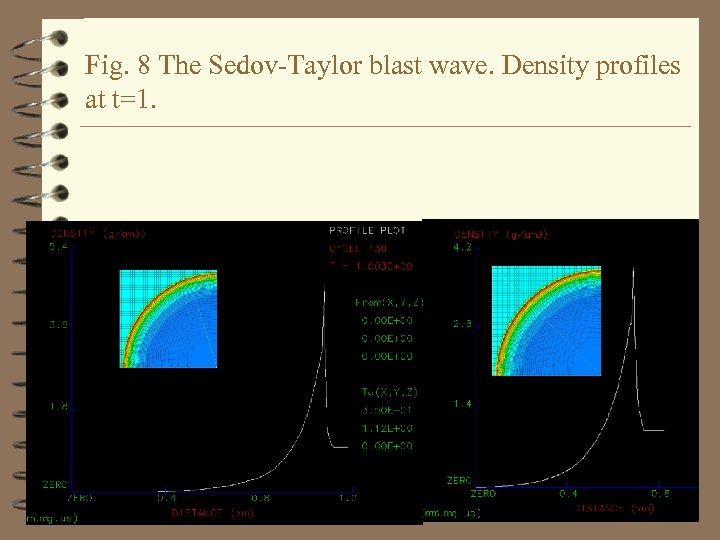Fig. 8 The Sedov-Taylor blast wave. Density profiles at t=1.

The Saltzman Problem 4 A piston moves with a velocity of u=10 into an almost cold ideal gas 4 This 1 D problem is solved on a 2 D mesh with planar symmetry 4 The 100 x 10 mesh shown above tests the propagation of a planar shock into an obliquelyinclined non-uniform mesh

Fig. 9 The Saltzman Problem. 100 x 10 Lagrange mesh at t=0. 7 (a) Scalar Q (b) SMG with uni-axial tensor q and NC (a) (b)

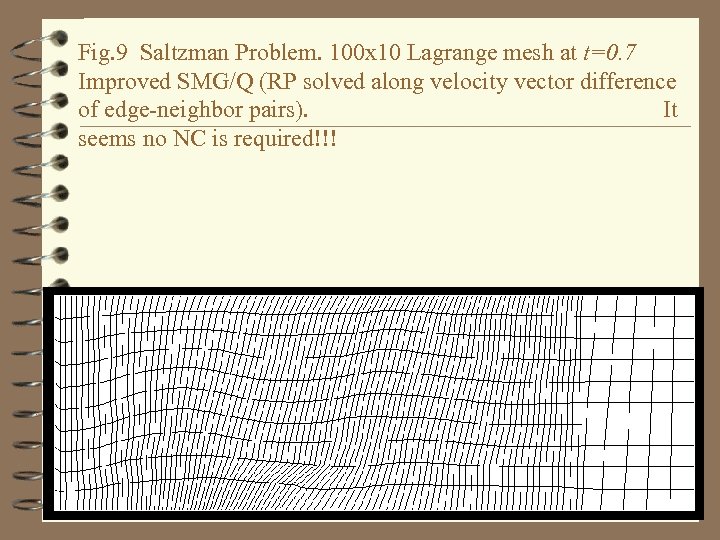Fig. 9 Saltzman Problem. 100 x 10 Lagrange mesh at t=0. 7 Improved SMG/Q (RP solved along velocity vector difference of edge-neighbor pairs). It seems no NC is required!!!

Cylindrical Noh Problem 4 with the data: 4 and analytic solution:

Cylindrical Noh problem 1 D Lagrangian mesh in 3 D code 4 3 D code can handle 1 D, 2 D mesh with axial symmetry. – The B. C. and the stability condition must be adjusted 4 A 100 equal size grid was used. 4 The over-shoot at the front might be caused by the use of the approximate RP solver in the 3 D code. An infinite strength shock in an ideal gas does not obey the linear shock to particle relationship. – t=0. 6

Cylindrical Noh problem 2 D ALE mesh in 3 D code 4 We consider a cylinder with a body-fitted grid which has 32 x 1 zones 4 There are symmetry planes at z=0, z=0. 05 4 The ALE grid motion keeps the mesh smooth while the outer radius shrinks

Cylindrical Noh problem 2 D ALE mesh in 3 D code at T=0. 6 (a) velocity plot (b) isobars

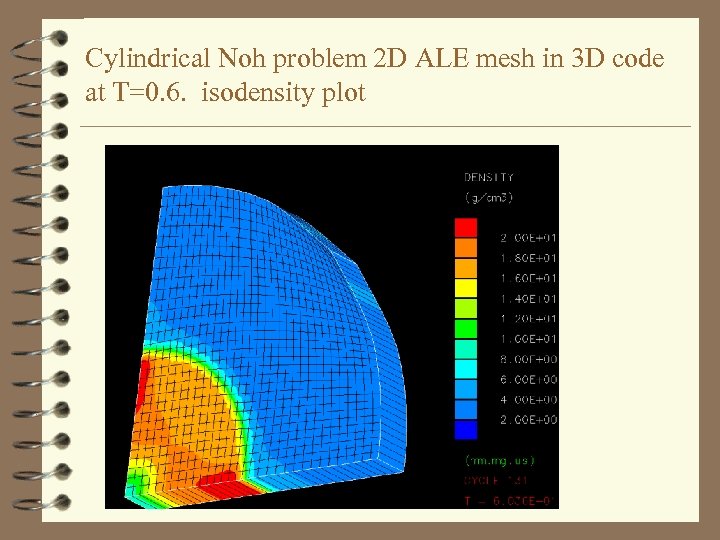Cylindrical Noh problem 2 D ALE mesh in 3 D code at T=0. 6. isodensity plot

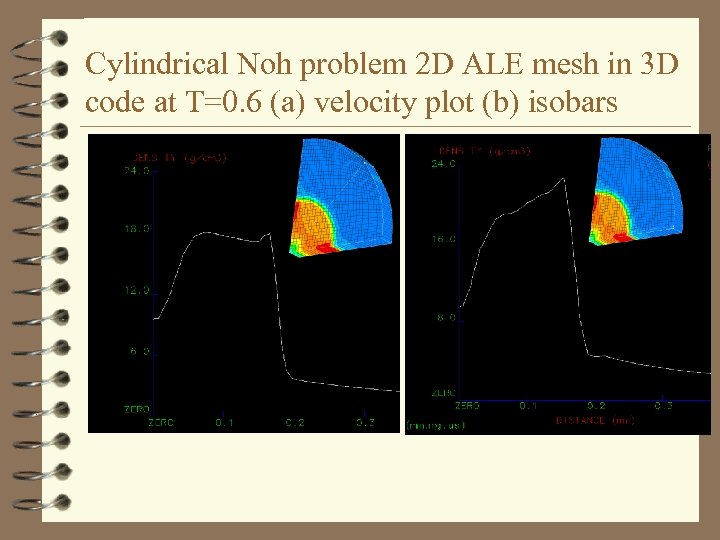Cylindrical Noh problem 2 D ALE mesh in 3 D code at T=0. 6 (a) velocity plot (b) isobars

Spherical Noh Problem 4 with the data: 4 and analytic solution: see Noh, Birman et. al.

3 D ALE mesh for Spherical Noh problem 4 The mesh is Cartesian. The ALE grid is uniformly contracting at a rate given by the grid velocity: 4 where is the velocity of a grid point at. is the spherical boundary at time t. 4 The 3 D mesh has 503 zones. The material boundary cuts through mesh zones.

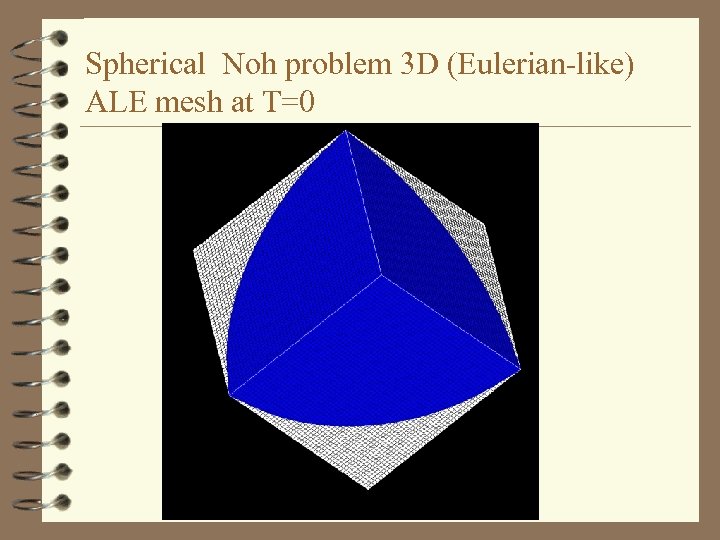Spherical Noh problem 3 D (Eulerian-like) ALE mesh at T=0

Spherical Noh problem 3 D (Eulerian-like) ALE mesh at T=0. 6. isobar plot

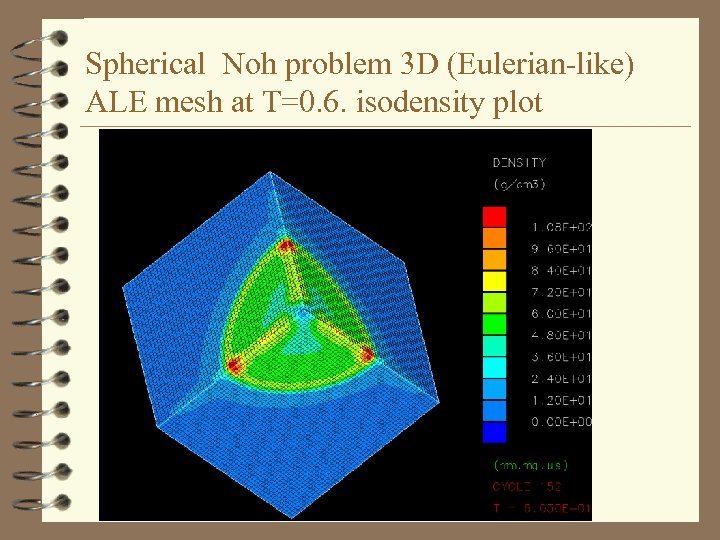Spherical Noh problem 3 D (Eulerian-like) ALE mesh at T=0. 6. isodensity plot

Concluding Remarks 4 SMG is a ‘dual scheme’. It is both a Godunov method and a classical-Lagrange method. 4 SMG/Q bridges the Lagrange-to-Godunov “conceptual gap”. 4 The second-order extension produces sharp shock capturing while minimizing entropy errors in regions of smooth compression. 4 The method can be applied to structured mesh, as well as to unstructured mesh.

Future Work 4 Improve the velocity limiter for multi-D structured and unstructured mesh 4 Explore alternate Q formulations: – Zone-centered “directional scalar Q” – Zone-centered “directional uni-axial tensor Q” 4 Elastic-plastic flow

References 4 Wilkins M. L. , "Calculation of Elastic-Plastic Flow”, Meth. Comp. 4 4 Phys. , 3, p 211, B. Alder et al. eds. , Academic Press (1964). van Leer B. , J. Comp. Phys. , 32, p 101, (1979). Ben Artzi M. , Falcovitz J. , "Generalized Riemann Problems in Computational Fluid Dynamics", Cambridge Univ. Press, London, (2003). Luttwak, G. , "Comparing Lagrangian Godunov and Pseudo-Viscosity Schemes for Multi-Dimensional Impact Simulations”, p 255 -258, Shock Compression of Condensed Matter-2001, Furnish M. D. et al Eds, (2002), AIP, CP 620. Luttwak, G. ”Staggered Mesh Godunov (SMG) Schemes for Lagrangian Hydrodynamics”, presented at the APS Topical Conference on Shock Compression of Condensed matter, Baltimore, MD, July 31 -Aug 5, 2005

References 4 4 4 4 Christensen R. B. , "Godunov Methods on a Staggered Mesh. An Improved Artificial Viscosity", L. L. N. L report UCRL-JC-105269, (1990). Benson D. J. , Schoenfeld S. , Comp. Mech. , 11, p 107 -121, (1993). Caramana E. J. , Shaskov M. J. , Whalen P. P. , J. Comp. Phys. 144, p 70, (1998). Margolin L. G. , LLNL report UCRL-5382, (1988) Noh F. W. , J. Comp. Phys. , 72, p 78, (1987) Sod G. , A. , J. Comp. Phys. , 27, p 1, (1978) Birman A. , Har’el N. Y. , Falcovitz J. , Ben-Artzi M. , Feldman U. , 22 nd Int. Symp. on Shock Waves, Imperial College, London, UK, July 18 -23, (1999)

More References 4 Luttwak G. , Cowler M. S. , "Remapping Techniques for Three Dimensional Meshes", presented at the 1999 Int. Workshop for New Models and Hydrocodes for Shock Wave Processes, held at the Univ. of Maryland, College Park, MD, (1999), to appear 4 Luttwak G. , "Interface Tracking in Eulerian and MMALE Calculations", p 283286, Shock Compression of Condensed Matter-2001, Furnish M. D. , et al. eds. , AIP, CP 620, (2002) 4 Luttwak G. , "On Rules for Grid Motion in 3 D ALE Codes", presented at the "New Models and Hydro-codes for Shock Wave Processes 2002", Edinburgh, Scotland, UK, May 2002, ed. by Klimenko V. Y. , to appear 4 Luttwak G. , "Partially Split Volume Integration scheme for the Advection Phase of Eulerian and MMALE Simulations", presented at the 2004 Int. Conf. for New Models and Hydro-codes for Shock Wave Processes, Univ. of Maryland, College Park, MD, 16 -21 May, 2004