bc1ebe0494b78196a4b76e9b34c6ad7b.ppt
- Количество слайдов: 41

Stability Analysis of Continuous. Time Switched Systems: A Variational Approach Michael Margaliot School of EE-Systems Tel Aviv University, Israel Joint work with: Michael S. Branicky (CWRU) Daniel Liberzon (UIUC) 1

Overview l l Switched systems Stability analysis: q A control-theoretic approach q A geometric approach q An integrated approach Conclusions 2
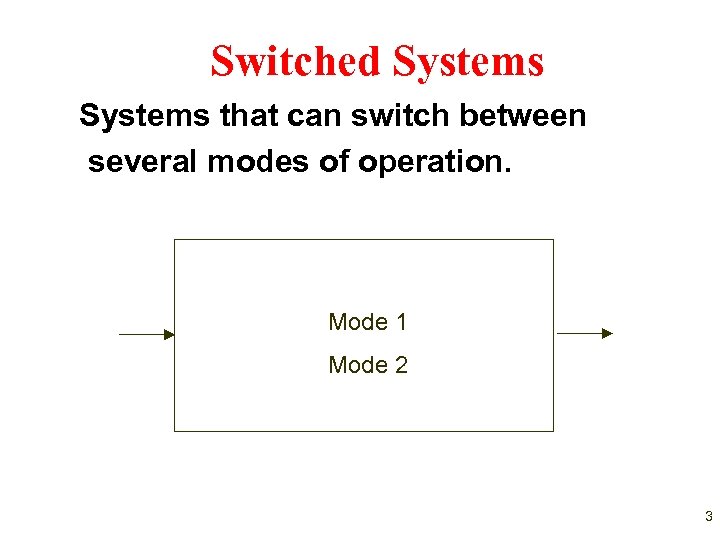
Switched Systems that can switch between several modes of operation. Mode 1 Mode 2 3
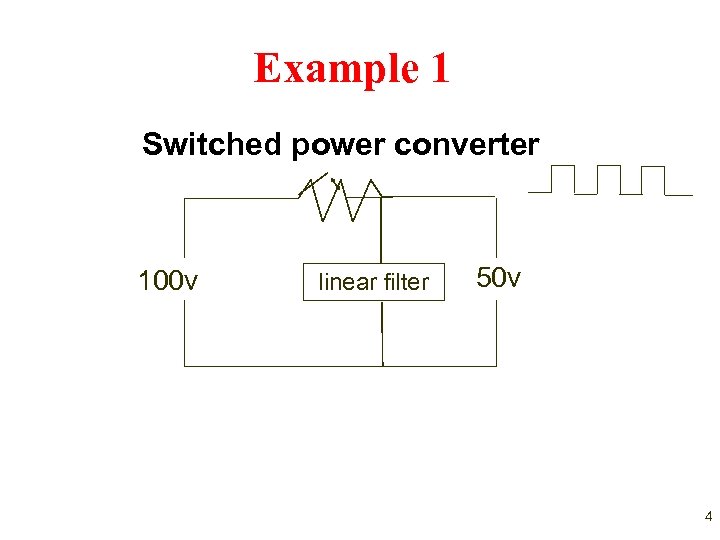
Example 1 Switched power converter 100 v linear filter 50 v 4
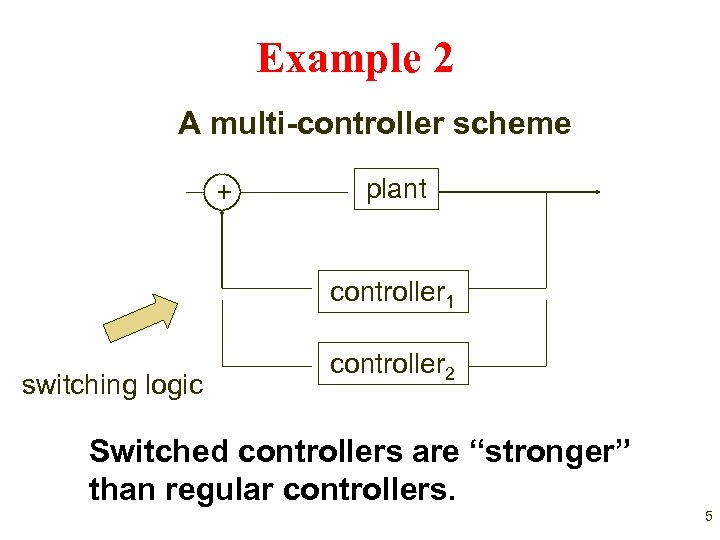
Example 2 A multi-controller scheme + plant controller 1 switching logic controller 2 Switched controllers are “stronger” than regular controllers. 5

More Examples l Air traffic control l Biological switches l Turbo-decoding l …… For more details, see: - Introduction to hybrid systems, Branicky - Basic problems in stability and design of switched systems, Liberzon & Morse 6

Synthesis of Switched Systems Driving: use mode 1 (wheels) Braking: use mode 2 (legs) The advantage: no compromise 7

Gestalt Principle “Switched systems are more than the sum of their subsystems. “ theoretically interesting practically promising 8

Differential Inclusions A solution is an absolutely continuous function satisfying (DI) for almost all t. Example: 9

Global Asymptotic Stability (GAS) Definition The differential inclusion is called GAS if for any solution (i) (ii) 10

The Challenge Why is stability analysis difficult? (i) A DI has an infinite number of solutions for each initial condition. (ii) The gestalt principle. 11
![Absolute Stability [Lure, 1944] 12 Absolute Stability [Lure, 1944] 12](https://present5.com/presentation/bc1ebe0494b78196a4b76e9b34c6ad7b/image-12.jpg)
Absolute Stability [Lure, 1944] 12

Absolute Stability The closed-loop system: A is Hurwitz, so CL is asym. stable for any Absolute Stability Problem Find For CL is asym. stable for any 13

Absolute Stability and Switched Systems Absolute Stability Problem Find 14
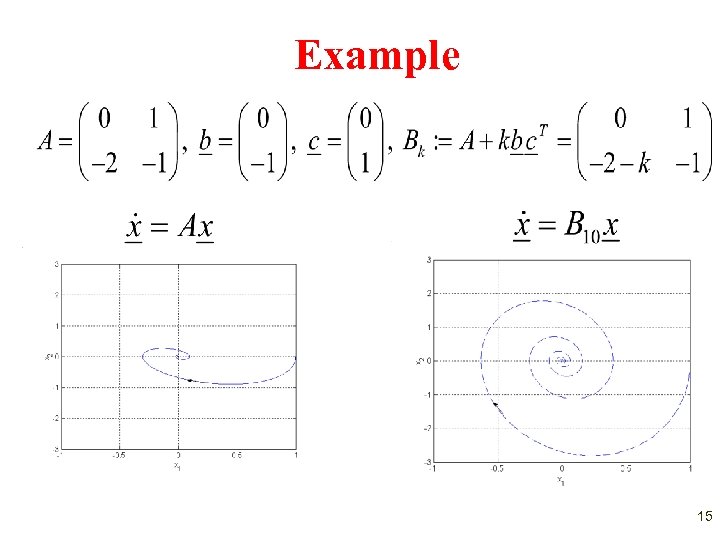
Example 15
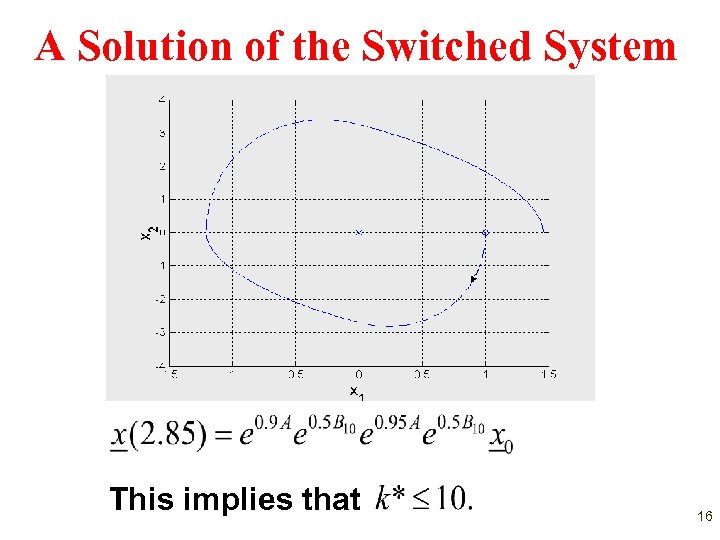
A Solution of the Switched System This implies that 16

Two Remarks Although both stable, and are is not stable. Instability requires repeated switching. 17

Optimal Control Approach Write system: Fix T as the bilinear control > 0. Define: Problem Find a control maximizing is the worst-case switching law (WCSL). Analyze the corresponding trajectory 18

Optimal Control Approach Consider as 19

Optimal Control Approach Theorem (Pyatnitsky) If (1) The function then: is finite, convex, positive, and homogeneous (i. e. ). (2) For every initial condition there exists a solution such that 20

Solving Optimal Control Problems is a functional: Two approaches: 1. Hamilton-Jacobi-Bellman (HJB) equation. 2. Maximum Principle. 21

HJB Equation Find such that Integrating: or An upper bound for , obtained for the maximizing Eq. (HJB). 22

The Case n=2 Margaliot & Langholz (2003) derived an explicit solution for when n=2. This yields an easily verifiable necessary and sufficient condition for stability of second-order switched linear systems. 23

Basic Idea The function of if We know that is a first integral so Thus, is a concatenation of two first integrals and 24
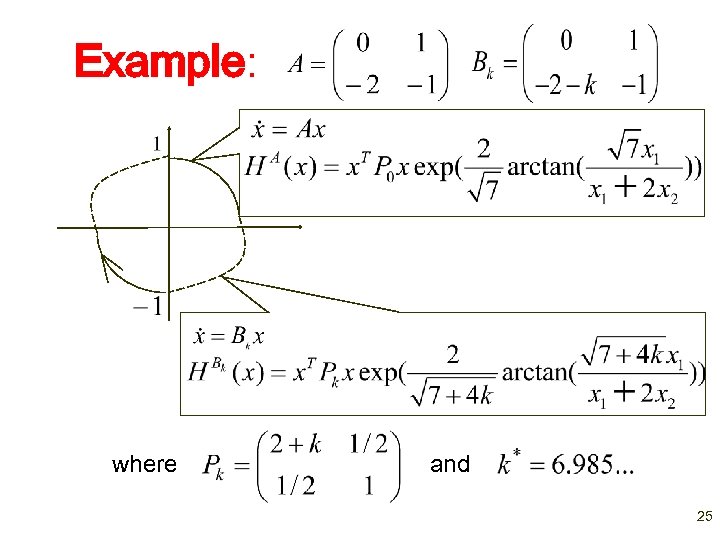
Example: where and 25
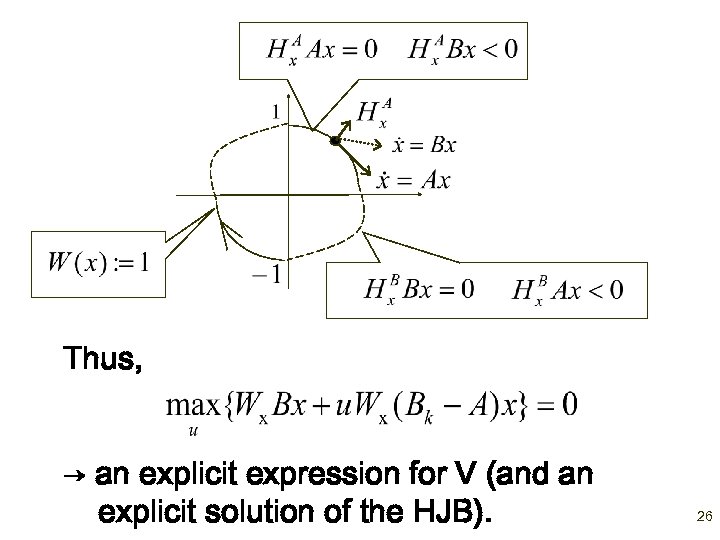
Thus, → an explicit expression for V (and an explicit solution of the HJB). 26

More on the Planar Case Theorem For a planar bilinear control system [Margaliot & Branicky, 2009] Corollary GAS of 2 nd-order positive linear switched systems. 27

Nonlinear Switched Systems where are GAS. Problem Find a sufficient condition guaranteeing GAS of (NLDI). 28

Lie-Algebraic Approach For simplicity, consider the linear differential inclusion: so 29

Commutation Relations and GAS Suppose that A and B commute, i. e. AB=BA, then Definition The Lie bracket of Ax and Bx is [Ax, Bx]: =ABx-BAx. Hence, [Ax, Bx]=0 implies GAS. 30

Lie Brackets and Geometry Consider Then: 31

Geometry of Car Parking This is why we can park our car. The term is the reason this takes so long. 32

Nilpotency Definition k’th order nilpotency: all Lie brackets involving k+1 terms vanish. 1 st order nilpotency: [A, B]=0 2 nd order nilpotency: [A, B]]=[B, [A, B]]=0 Q: Does k’th order nilpotency imply GAS? 33

Known Results Linear switched systems: l k = 2 implies GAS (Gurvits, 1995). l k’th order nilpotency implies GAS (Liberzon, Hespanha, & Morse, 1999) (Kutepov, 1982) Nonlinear switched systems: l k = 1 implies GAS (Mancilla-Aguilar, 2000). l An open problem: higher orders of k? (Liberzon, 2003) 34

A Partial Answer Theorem (Margaliot & Liberzon, 2004) 2 nd order nilpotency implies GAS. Proof By the PMP, the WCSL satisfies Let 35

Then 1 st order nilpotency Differentiating again yields: 2 nd order nilpotency up to a single switch in the WCSL. 36

Handling Singularity If m(t) 0, the Maximum Principle does not necessarily provide enough information to characterize the WCSL. Singularity can be ruled out using the notion of strong extremality (Sussmann, 1979). 37

3 rd Order Nilpotency In this case: further differentiation cannot be carried out. 38

3 rd Order Nilpotency Theorem (Sharon & Margaliot, 2007) 3 rd order nilpotency implies Proof (1) Hall-Sussmann canonical system; (2) A second-order MP (Agrachev&Gamkrelidze). 39

Conclusions l Switched systems and differential inclusions are important in various scientific fields, and pose interesting theoretical questions. l Stability analysis is difficult. A natural and powerful idea is to consider the “most unstable” trajectory. 40

More info on the variational approach: “Stability analysis of switched systems using variational principles: an introduction”, Automatica 42(12): 20592077, 2006. Available online: www. eng. tau. ac. il/~michaelm 41
bc1ebe0494b78196a4b76e9b34c6ad7b.ppt