СТ АТ ИС ТИ КА
ПАРАМЕТРЫ ВЫБОРОК Математическое ожидание (mean) Для непрерывной случайной величины: b M(X)= a Для дискретной случайной величины: n
ПАРАМЕТРЫ ВЫБОРОК Дисперсия Для непрерывной случайной величины: b D(X)= a Для дискретной случайной величины: D(X)= /n
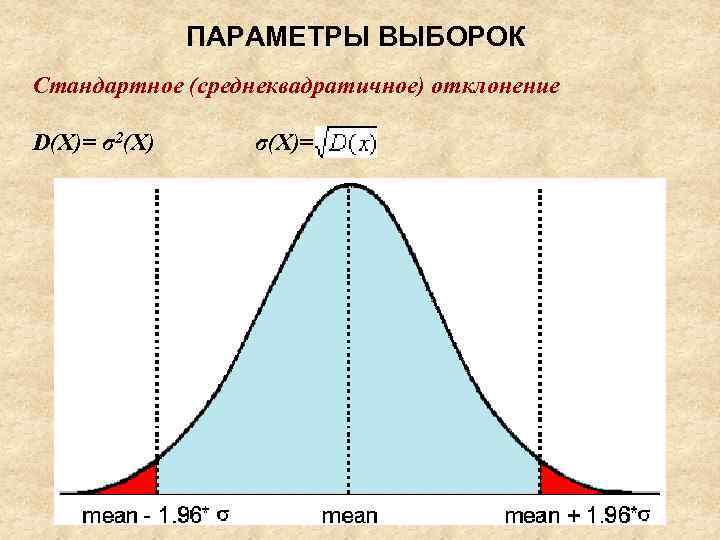ПАРАМЕТРЫ ВЫБОРОК Стандартное (среднеквадратичное) отклонение D(X)= σ2(X) σ(X)=
СВОБОДНЫЕ И СВЯЗАННЫЕ ВЫБОРКИ Определение: Свободными (независимыми) выборками называются выборки данных, полученные на разном физически независимом друг с другом материале. Определение: Связанными (зависимыми) выборками называются выборки данных, полученные на одном и том же материале в разных условиях.
ТИПЫ КРИТЕРИЕВ ОЦЕНКИ КОЛИЧЕСТВЕННЫХ ПАРАМЕТРОВ • Параметрические критерии предполагают, что выборка порождена нормальным распределением. Преимущество этих критериев в том, что они более мощные. Если выборка удовлетворяет дополнительным предположениям, то параметрические критерии дают более точные результаты. • Непараметрические критерии не опираются на дополнительные предположения о распределении. В частности, к этому типу критериев относится большинство ранговых критериев. • Гипотезы о виде распределения проверяются с помощью критериев согласия.
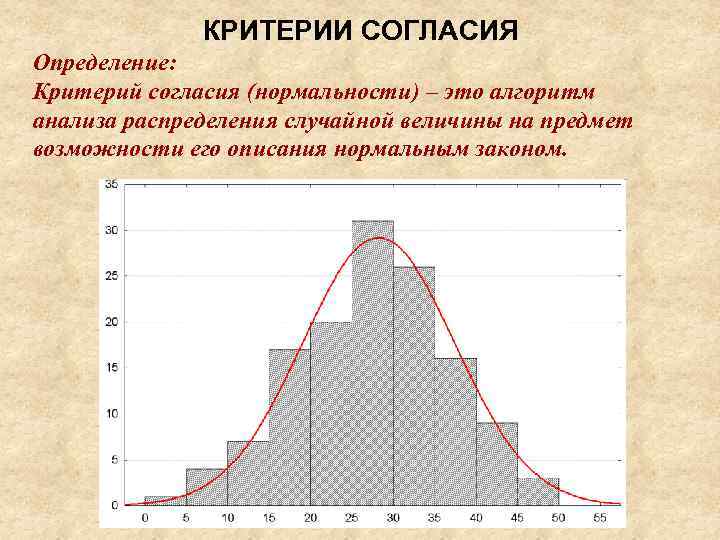КРИТЕРИИ СОГЛАСИЯ Определение: Критерий согласия (нормальности) – это алгоритм анализа распределения случайной величины на предмет возможности его описания нормальным законом.
КРИТЕРИЙ СОГЛАСИЯ КОЛМОГОРОВА Критерий согласия Колмогорова применяется для проверки правильности подбора теоретического распределения. Для его применения нужно найти максимальную по модулю разность между теоретической F(x) и эмпирической : D – максимальное значение разности между эмпирическими и теоретическими частотами; – сумма эмпирических частот.
t – КРИТЕРИЙ СТЬЮДЕНТА Критерий Стьюдента был разработан английским химиком У. Госсетом, когда он работал на пивоваренном заводе Гиннеса и по условиям контракта не имел права открытой публикации своих исследований. Публикации своих статей по t-критерию У. Госсет сделал в 1908 г. в журнале "Биометрика" под псевдонимом "Student". Простота вычисления t-критерия Стьюдента, а также его наличие в большинстве статистических пакетов и программ привели к широкому использованию этого критерия даже в тех условиях, когда он неприменим.
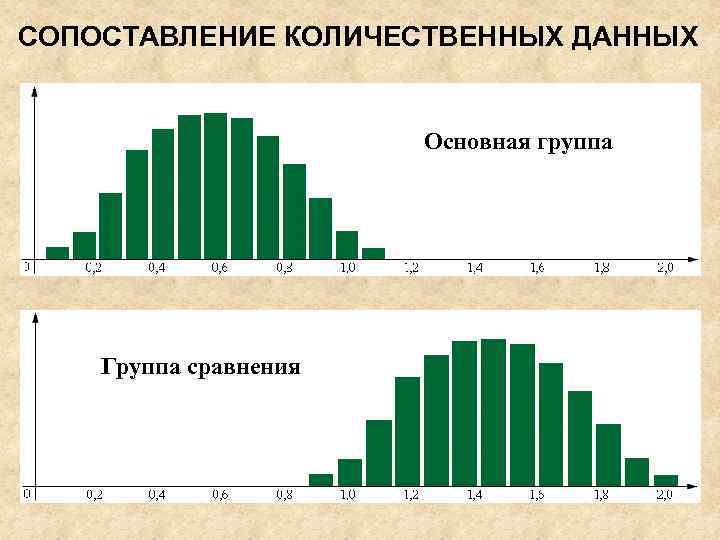СОПОСТАВЛЕНИЕ КОЛИЧЕСТВЕННЫХ ДАННЫХ Основная группа Группа сравнения
t – КРИТЕРИЙ СТЬЮДЕНТА Cтандартная ошибка разности средних арифметических для случая несвязанных выборок: n 1 и n 2 соответственно величины первой и второй выборки. t _ _ x и y – средние значения в основной и контрольной группах.
t – КРИТЕРИЙ СТЬЮДЕНТА Cтандартная ошибка разности средних арифметических для случая связанных выборок: n 1 = n 2 = n соответственно величина как первой, так и второй выборки. t _ _ x и y – средние значения в основной и контрольной группах.
ПРИМЕР РАСЧЕТА t-КРИТЕРИЯ Пример. В двух группах учащихся – основной и контрольной, получены следующие результаты по учебному предмету (тестовые баллы): Первая группа (экспериментальная) N 1 = 11 12 14 13 16 11 9 13 15 15 18 14 Вторая группа (контрольная) N 2=9 13 9 11 10 7 6 8 10 11
ПРИМЕР РАСЧЕТА t-КРИТЕРИЯ Общее количество членов выборки: n 1 = 11, n 2 = 9. Расчет средних арифметических: Хср = 13, 636; Yср = 9, 444 Стандартное отклонение: sx=2, 460; sy=2, 186 t t = 3, 981 табличное t = 2, 10 соответствует p = 0. 05 3, 981>2, 10
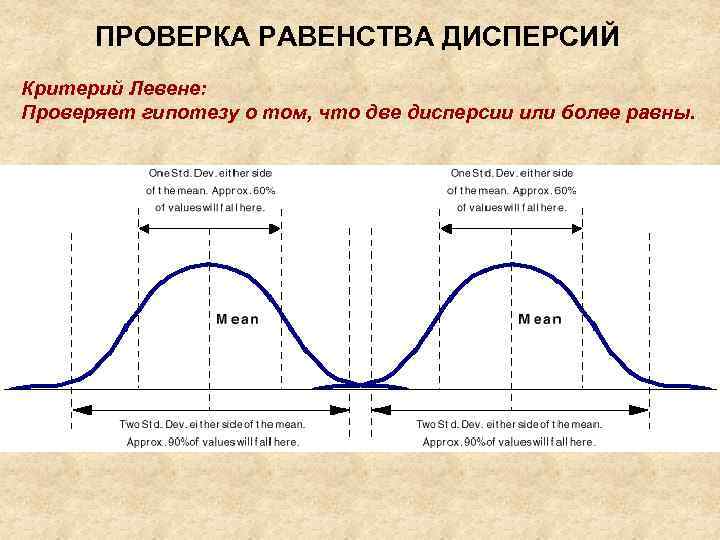ПРОВЕРКА РАВЕНСТВА ДИСПЕРСИЙ Критерий Левене: Проверяет гипотезу о том, что две дисперсии или более равны.
ЛИТЕРАТУРА http: //www. ami. nstu. ru/~headrd/seminar/Kontrol_Q/new%20 normal%20%20 r ed. htm http: //www. hi-edu. ru/e-books/xbook 096/01/index. html? part-007. htm http: //hm. tpu. ru/Geologi/galanov/html/L 6/sld 023. htm http: //www. statsoft. ru/home/portal/applications/Multivariatadvisor/TStudent/T-Student. htm http: //www. tspu. tula. ru/res/math/mop/lections/lection_6. htm http: //modeling. at. ua/publ/6 -1 -0 -22 http: //edu-main. narod. ru/math/statistica_book/gl 12. html