СТ АТ ИС ТИ К А
КОРРЕЛЯЦИЯ Определение: Корреляция – это статистическая взаимосвязь двух или нескольких случайных величин (либо величин, которые можно с некоторой допустимой степенью точности считать таковыми). При этом, изменения одной или нескольких из этих величин приводят к систематическому изменению другой или других величин. Математической мерой Корреляции двух случайных величин служит коэффициент Корреляции. 2
Метод сравнения параллельных рядов Приводится ряд данных по одному признаку и параллельно с ним по другому признаку, связь с которым предполагается. По вариации признака в первом и втором ряду судят о наличии связи признаков. Такой метод позволяет вывести только направление связи, но не измерить ее. 3
• Графический метод может использоваться как самостоятельно, так и совместно с другими методами. Если конкретные данные перенести на график, то получим поле точек. На оси абсцисс откладываются значения факторного признака x, а на оси ординат – значения результативного признака y. Каждая единица, обладающая определенным значением факторного и результативного признака, обозначается точкой. По совместному расположению точек на графике делают вывод о направлении и наличии зависимости 4
• Беспорядочное расположение говорит об отсутствии связи. Напротив, чем сильнее связь, тем теснее точки группируются вокруг определенной линии. Если точки на графике концентрируются вокруг прямой, идущей снизу вверх, зависимость между признаками прямая. Если точки концентрируются вокруг прямой, спускающейся сверху вниз, то это свидетельствует о наличии обратной зависимости. 5
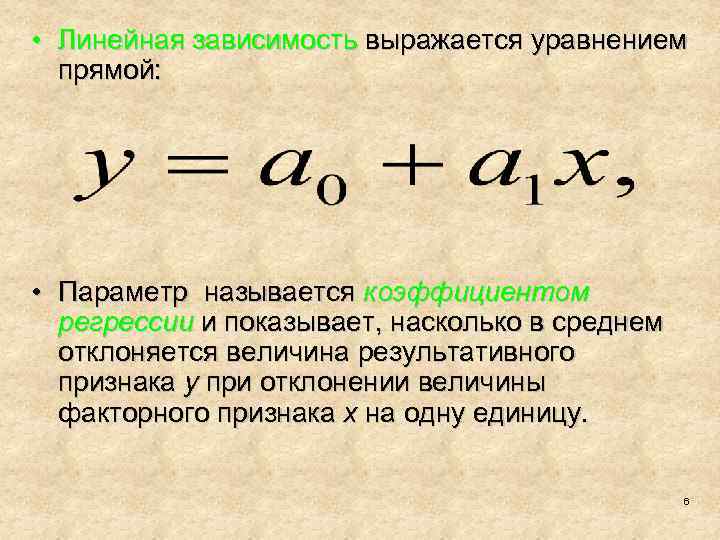• Линейная зависимость выражается уравнением прямой: • Параметр называется коэффициентом регрессии и показывает, насколько в среднем отклоняется величина результативного признака y при отклонении величины факторного признака x на одну единицу. 6
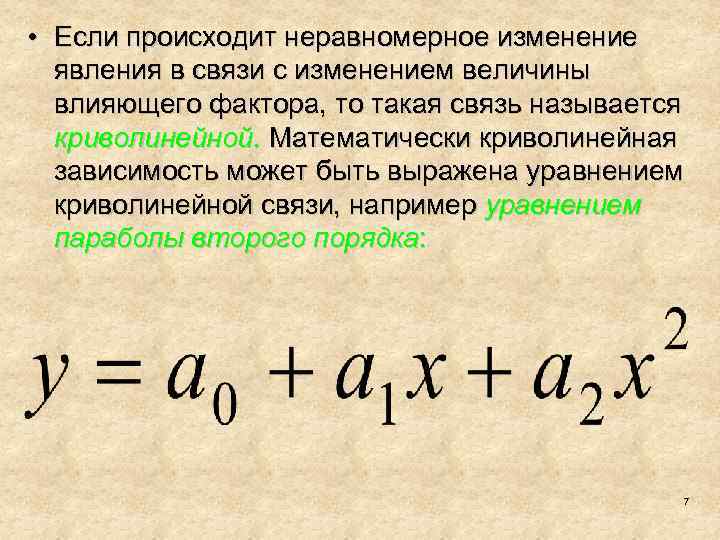• Если происходит неравномерное изменение явления в связи с изменением величины влияющего фактора, то такая связь называется криволинейной. Математически криволинейная зависимость может быть выражена уравнением криволинейной связи, например уравнением параболы второго порядка: 7
Аналитическое выражение связи. • Аналитические методы – основной способ изучения связи. Они делятся на непараметрические и параметрические. Применение методов корреляционного анализа дает возможность выражать связь между признаками аналитически (в виде уравнения) и придавать ей количественное выражение. 8
КОРРЕЛЯЦИОННЫЕ ПОЛЯ
КОРРЕЛЯЦИЯ Математической мерой Корреляции двух случайных величин служит коэффициент корреляции. Значения коэффициента К. располагаются по шкале от 0 до 1, 00, характеризуя степень взаимоотношения от полного отсутствия К. до полной К. Когда r = 0, 60, а r(2) = 0, 36, то можно сказать, что 36% отклонения в переменной Y коррелируют с колебаниями в переменной Х; или же что 64% отклонения не коррелируют.
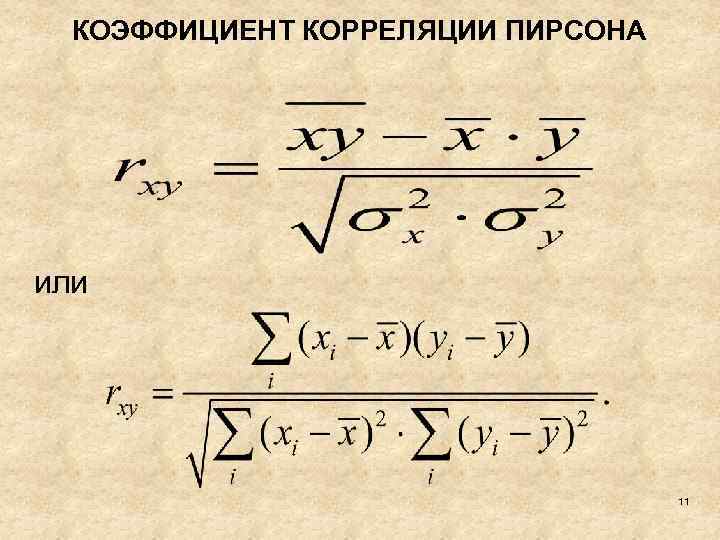КОЭФФИЦИЕНТ КОРРЕЛЯЦИИ ПИРСОНА или 11
КОРРЕЛЯЦИЯ СПИРМЕНА Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется степень связи между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
КОРРЕЛЯЦИЯ СПИРМЕНА Коэффициент ранговой корреляции Спирмена - это непараметрический метод, который используется с целью статистического изучения связи между явлениями. В этом случае определяется степень связи между двумя количественными рядами изучаемых признаков и дается оценка тесноты установленной связи с помощью количественно выраженного коэффициента.
Практический расчет коэффициента ранговой корреляции Спирмена включает следующие этапы: 1) Сопоставить ранг каждому из признаков. 2) Определить разности рангов каждой пары сопоставляемых значений. 3) Возвести в квадрат каждую разность и суммировать полученные результаты. 4) Вычислить коэффициент корреляции рангов по формуле: - сумма квадратов разностей рангов, n - число парных наблюдений.
КОРРЕЛЯЦИЯ КЕНДАЛЛА Применяется для выявления взаимосвязи между количественными или качественными показателями, если их можно ранжировать. Значения показателя X выставляют в порядке возрастания и присваивают им ранги. Ранжируют значения показателя Y и рассчитывают коэффициент Корреляции Кенделла: , где S = P − Q. P – суммарное число наблюдений, следующих за текущими наблюдениями с большим значением рангов Y. Q – суммарное число наблюдений, следующих за текущими наблюдениями с меньшим значением рангов Y. (Равные ранги не учитываются!)
ЛИТЕРАТУРА http: //forexaw. com/TERMs/Exchange_Economy/Macroeconomic_indicators/ Finance/l 675_Корреляция_Correlation http: //planetcalc. ru/527/ http: //www. infamed. com/stat/s 05. html http: //www. vashpsixolog. ru/lectures-on-the-psychology/134 -otherpsychology/1055 -matematicheskie-metody-obrabotki-psixologicheskixdannyx? start=11 http: //forum. orlovs. pp. ru/viewtopic. php? t=71 http: //www. kgafk. ru/kgufk/html/korandreg 2. html http: //www. nbuv. gov. ua/portal/natural/SOI/2007_1/Zaxarov. pdf