SSAC 2006 Q 199 CC 1 2 Is

SSAC 2006. Q 199. CC 1. 2 Is It Hot in Here? Spreadsheeting Conversions in the English and the Metric Systems Core Quantitative concept and skill Number sense: Unit conversions In the lab, all measurements are done using the metric system (SI System). This module will familiarize you with the SI units of mass, volume, and temperature. Prepared for SSAC by Cheryl Coolidge - Colby-Sawyer College Supporting Quantitative concepts and skills • Number sense: Scientific notation; ratios; order of magnitude • Algebra: Rearranging equations • Graphs: XY (scatter); trend line • Function: Linear © The Washington Center for Improving the Quality of Undergraduate Education. All rights reserved. 2006 1

Overview of Module The process of unit conversion allows you to convert a quantity from one system of measurement to another, or to convert within a system of measurement. Some cases, such as temperature scales, require using known formulas. Slide 3 presents the problem for you to solve. Slides 4 - 6 introduce you to the use of spreadsheets to perform calculations efficiently. Slide 7 explains the use of conversion factors. Slides 8 and 9 provide you with the metric prefixes and review scientific notation. Slides 10 – 12 require you to create spreadsheets to perform conversions of temperature, volume, and mass. Slide 13 asks you to create an XY scatter graph using your mass conversions, and to add a trendline to your graph. Slide 14 gives you the opportunity to practice using trendlines with the temperature conversions and introduces you to the TREND function. Slides 15 – 16 contain the end of module assignments. 2

Problem The metric system is used to record measurements in most industrial countries of the world and in science laboratories in all countries. This module will allow you to become more familiar with metric units and to learn how to perform conversions. 1. Suppose you are instructed to weigh out 60 grams of sodium chloride (table salt). Will that make your French fries salty? 2. Suppose your dorm room is 55 degrees Celsius. Should you get facilities to help you? 3. Suppose your next door neighbor offers you 25 milliliters of Sam Adams for $5. 00. Will you have a good party? 3

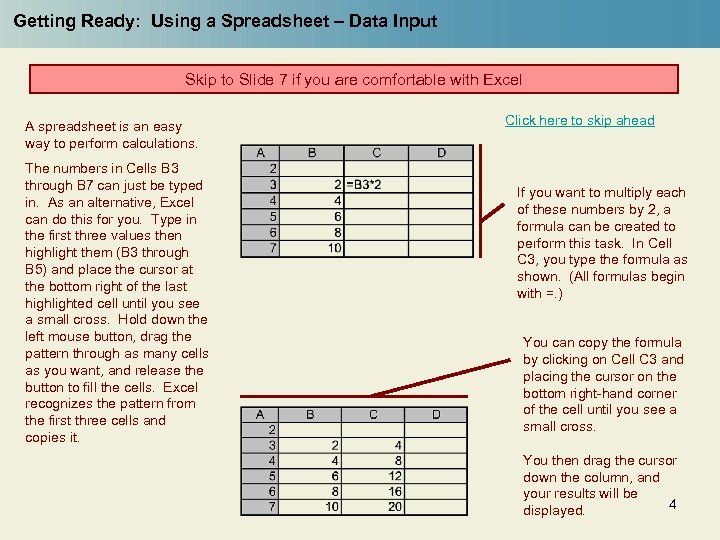Getting Ready: Using a Spreadsheet – Data Input Skip to Slide 7 if you are comfortable with Excel A spreadsheet is an easy way to perform calculations. The numbers in Cells B 3 through B 7 can just be typed in. As an alternative, Excel can do this for you. Type in the first three values then highlight them (B 3 through B 5) and place the cursor at the bottom right of the last highlighted cell until you see a small cross. Hold down the left mouse button, drag the pattern through as many cells as you want, and release the button to fill the cells. Excel recognizes the pattern from the first three cells and copies it. Click here to skip ahead If you want to multiply each of these numbers by 2, a formula can be created to perform this task. In Cell C 3, you type the formula as shown. (All formulas begin with =. ) You can copy the formula by clicking on Cell C 3 and placing the cursor on the bottom right-hand corner of the cell until you see a small cross. You then drag the cursor down the column, and your results will be 4 displayed.

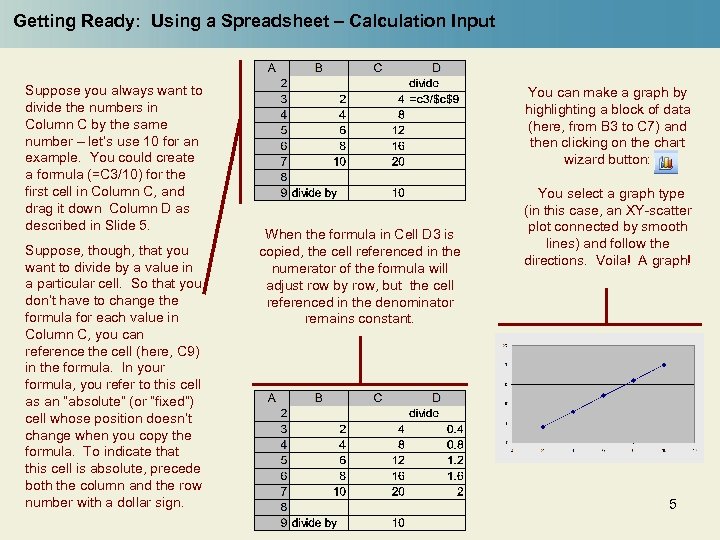Getting Ready: Using a Spreadsheet – Calculation Input Suppose you always want to divide the numbers in Column C by the same number – let’s use 10 for an example. You could create a formula (=C 3/10) for the first cell in Column C, and drag it down Column D as described in Slide 5. Suppose, though, that you want to divide by a value in a particular cell. So that you don’t have to change the formula for each value in Column C, you can reference the cell (here, C 9) in the formula. In your formula, you refer to this cell as an “absolute” (or “fixed”) cell whose position doesn’t change when you copy the formula. To indicate that this cell is absolute, precede both the column and the row number with a dollar sign. You can make a graph by highlighting a block of data (here, from B 3 to C 7) and then clicking on the chart wizard button: When the formula in Cell D 3 is copied, the cell referenced in the numerator of the formula will adjust row by row, but the cell referenced in the denominator remains constant. You select a graph type (in this case, an XY-scatter plot connected by smooth lines) and follow the directions. Voila! A graph! 5

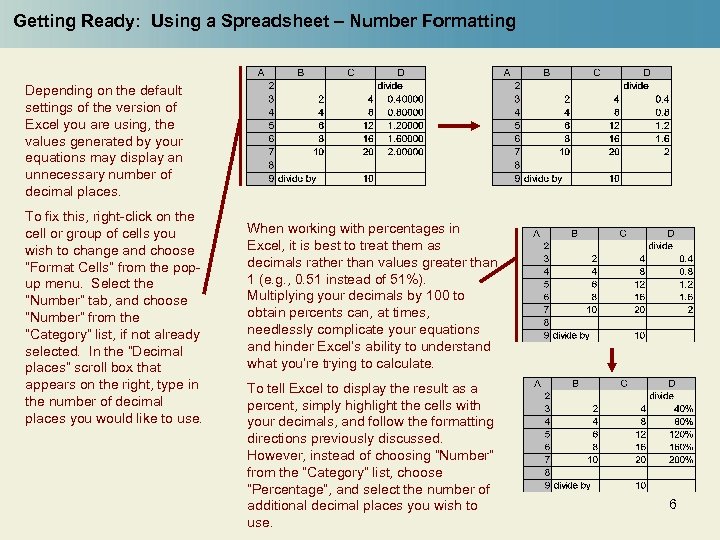Getting Ready: Using a Spreadsheet – Number Formatting Depending on the default settings of the version of Excel you are using, the values generated by your equations may display an unnecessary number of decimal places. To fix this, right-click on the cell or group of cells you wish to change and choose “Format Cells” from the popup menu. Select the “Number” tab, and choose “Number” from the “Category” list, if not already selected. In the “Decimal places” scroll box that appears on the right, type in the number of decimal places you would like to use. When working with percentages in Excel, it is best to treat them as decimals rather than values greater than 1 (e. g. , 0. 51 instead of 51%). Multiplying your decimals by 100 to obtain percents can, at times, needlessly complicate your equations and hinder Excel’s ability to understand what you’re trying to calculate. To tell Excel to display the result as a percent, simply highlight the cells with your decimals, and follow the formatting directions previously discussed. However, instead of choosing “Number” from the “Category” list, choose “Percentage”, and select the number of additional decimal places you wish to use. 6

Getting ready: conversion factors A conversion factor is a ratio that expresses an equality between two units. For example, there are 12 inches per foot. This fact can be stated as an equation: 12 inches = 1 foot. The equation can be rearranged to produce two conversion factors, each equal to one: 12 inches =1 1 foot and 1 foot =1 12 inches The form of a ratio is always Numerator Denominator Multiplying a number by a conversion factor is essentially multiplying the number by one, which does not change the amount that the number represents. 3× 2=3 You choose the form of your conversion factor based on what units you need to 2 eliminate and what units you want in your final answer. If you were converting 100 and 3 × ft = 3 ft inches to feet, the correct form of the conversion factor should have the desired unit (feet) and its associated number (1) in the numerator, and the unwanted unit (inches) and its number (12) in the denominator. When you multiply your starting value of 100 inches by the conversion factor, you end up with inches in the numerator and inches in the denominator, which is a quantity equal to one that can be eliminated: 100 inches × 1 foot = 100 × 1 foot = 8. 33 feet 12 inches 12 Note – You can “chain” conversion factors as needed. If you wanted to convert inches to miles, you could use one factor to convert inches to feet, followed by a second factor converting feet to miles. 7

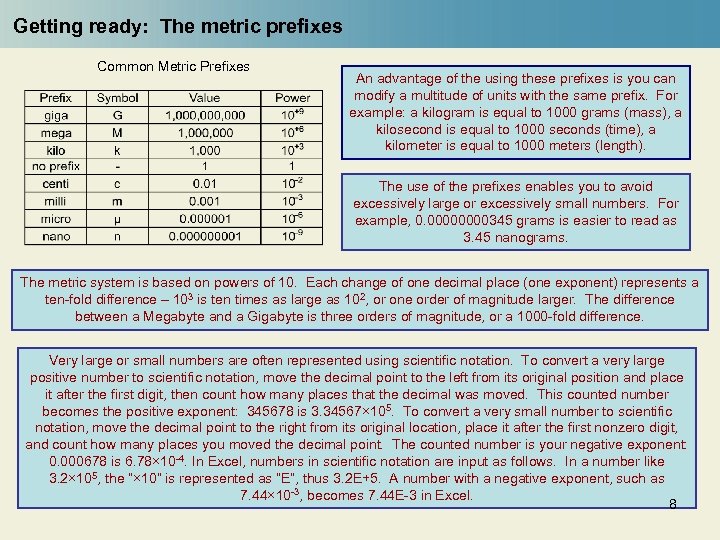Getting ready: The metric prefixes Common Metric Prefixes An advantage of the using these prefixes is you can modify a multitude of units with the same prefix. For example: a kilogram is equal to 1000 grams (mass), a kilosecond is equal to 1000 seconds (time), a kilometer is equal to 1000 meters (length). The use of the prefixes enables you to avoid excessively large or excessively small numbers. For example, 0. 0000345 grams is easier to read as 3. 45 nanograms. The metric system is based on powers of 10. Each change of one decimal place (one exponent) represents a ten-fold difference – 103 is ten times as large as 102, or one order of magnitude larger. The difference between a Megabyte and a Gigabyte is three orders of magnitude, or a 1000 -fold difference. Very large or small numbers are often represented using scientific notation. To convert a very large positive number to scientific notation, move the decimal point to the left from its original position and place it after the first digit, then count how many places that the decimal was moved. This counted number becomes the positive exponent: 345678 is 3. 34567× 105. To convert a very small number to scientific notation, move the decimal point to the right from its original location, place it after the first nonzero digit, and count how many places you moved the decimal point. The counted number is your negative exponent: 0. 000678 is 6. 78× 10 -4. In Excel, numbers in scientific notation are input as follows. In a number like 3. 2× 105, the “× 10” is represented as “E”, thus 3. 2 E+5. A number with a negative exponent, such as 7. 44× 10 -3, becomes 7. 44 E-3 in Excel. 8

Getting ready: metric conversions One of the biggest advantages of the metric system is that you do not need to use complicated ratios to change from one unit to another. All conversions are based on powers of 10, unlike the English system, where conversions are quite cumbersome (12 inches/foot, 5280 feet/mile). Once you have a feel for the units of the metric system, you do not need to use conversion ratios. Simply look at the difference (absolute value) between the exponents of the unit you are converting from and the unit you are converting to. For example, suppose that you want to convert 7. 11 milligrams to kilograms. The difference between the exponent in kilograms (+3) and the exponent in milligrams (-3) is 6. If the unit you are converting from is SMALLER than the unit you are converting to (as in the example), multiply the original value by 10 negative difference to convert to the new unit. If the unit you are converting from is LARGER than the new unit, multiply the original value by 10 positive difference to convert to the new unit. Therefore, 7. 11 milligrams is equal to 7. 11× 10 -6 kilograms. In Excel, you would multiply 7. 11 by 1 E-6 to make the conversion. If the number you are converting is already in scientific notation, add the difference between the exponents to the existing exponent if you are converting to a smaller unit, or subtract the difference if converting to a larger unit. Thus, converting 7. 11× 102 milligrams to kilograms will give you 7. 11× 10 -4 kilograms (the original exponent of 2 minus the difference of 6). Explain how to perform the following conversions and record your answers. 1. 66 grams to centigrams 2. 7. 524 kiloliters to microliters 3. 856 nanograms to milligrams 9

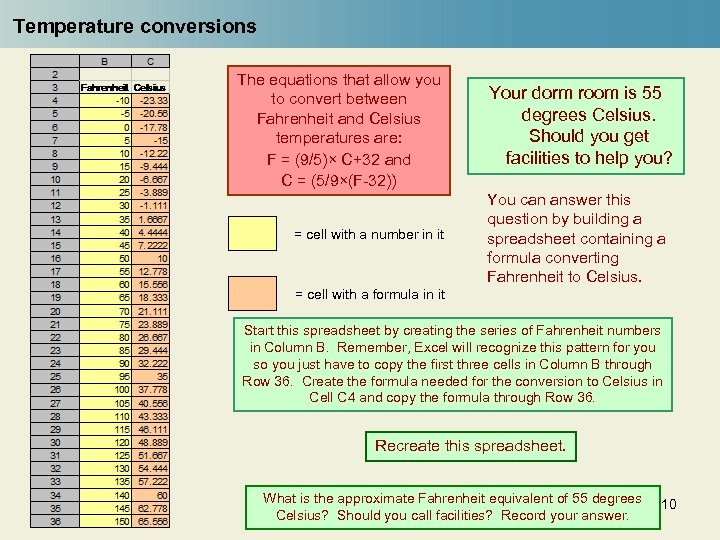Temperature conversions The equations that allow you to convert between Fahrenheit and Celsius temperatures are: F = (9/5)× C+32 and C = (5/9×(F-32)) = cell with a number in it Your dorm room is 55 degrees Celsius. Should you get facilities to help you? You can answer this question by building a spreadsheet containing a formula converting Fahrenheit to Celsius. = cell with a formula in it Start this spreadsheet by creating the series of Fahrenheit numbers in Column B. Remember, Excel will recognize this pattern for you so you just have to copy the first three cells in Column B through Row 36. Create the formula needed for the conversion to Celsius in Cell C 4 and copy the formula through Row 36. Recreate this spreadsheet. What is the approximate Fahrenheit equivalent of 55 degrees Celsius? Should you call facilities? Record your answer. 10

Volume conversions Your next door neighbor offers you 25 milliliters of Sam Adams for $5. 00. Will you have a good party? There are 16 tablespoons in a cup, 4 cups in a quart, 4 quarts in a gallon, and 1 liter is equal to 1. 06 quarts. As before, use a spreadsheet to convert to familiar units. Create a column of milliliters, starting with 5 mls and incrementing by 5 mls till you have 150 mls. = Cell with a number = Cell with a formula Recreate this spreadsheet, starting on a new sheet. So, how many tablespoons are in 25 mls? Will you invite this neighbor to your party? 11

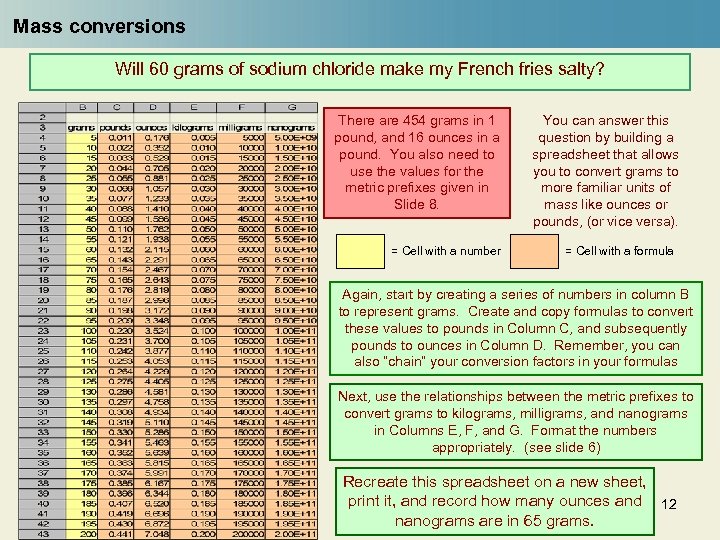Mass conversions Will 60 grams of sodium chloride make my French fries salty? There are 454 grams in 1 pound, and 16 ounces in a pound. You also need to use the values for the metric prefixes given in Slide 8. = Cell with a number You can answer this question by building a spreadsheet that allows you to convert grams to more familiar units of mass like ounces or pounds, (or vice versa). = Cell with a formula Again, start by creating a series of numbers in column B to represent grams. Create and copy formulas to convert these values to pounds in Column C, and subsequently pounds to ounces in Column D. Remember, you can also “chain” your conversion factors in your formulas Next, use the relationships between the metric prefixes to convert grams to kilograms, milligrams, and nanograms in Columns E, F, and G. Format the numbers appropriately. (see slide 6) Recreate this spreadsheet on a new sheet, print it, and record how many ounces and 12 nanograms are in 65 grams.

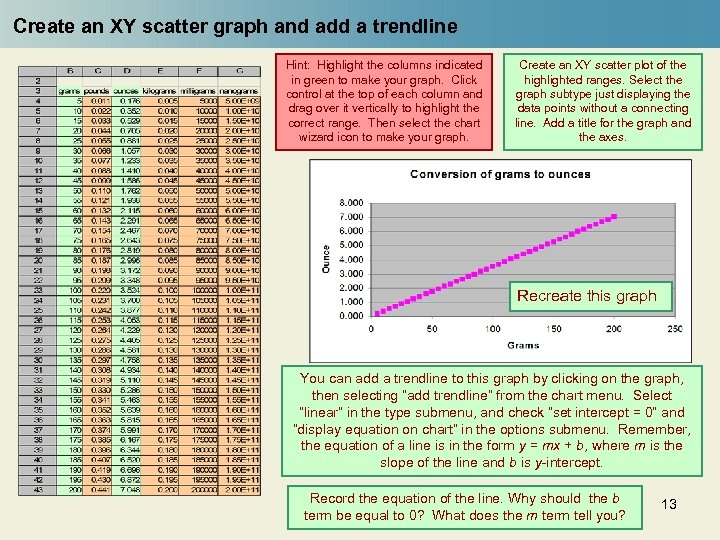Create an XY scatter graph and add a trendline Hint: Highlight the columns indicated in green to make your graph. Click control at the top of each column and drag over it vertically to highlight the correct range. Then select the chart wizard icon to make your graph. Create an XY scatter plot of the highlighted ranges. Select the graph subtype just displaying the data points without a connecting line. Add a title for the graph and the axes. Recreate this graph You can add a trendline to this graph by clicking on the graph, then selecting “add trendline” from the chart menu. Select “linear“ in the type submenu, and check “set intercept = 0” and “display equation on chart” in the options submenu. Remember, the equation of a line is in the form y = mx + b, where m is the slope of the line and b is y-intercept. Record the equation of the line. Why should the b term be equal to 0? What does the m term tell you? 13

Using trendlines to look at temperature conversions; the TREND function Refer back to the spreadsheet you created to convert Fahrenheit temperatures to Celsius. Make a copy of the Fahrenheit column by highlighting from B 4 through B 36. Select copy from the edit menu, place the cursor on Cell D 4 and select paste from the edit menu. Highlight Cells C 4 through D 36 and create an XY scatter graph as before. Your x-axis is the Celsius data and the y-axis is composed of the Fahrenheit equivalents. Add the linear trendline and display the equation on the graph. DO NOT set the intercept = 0. (Why? ) Record the equation of the line. Where have you seen a similar equation in this module? Now highlight Cells B 4 through C 36 and create an XY scatter graph as before. Your xaxis is now the Fahrenheit data and the y-axis is composed of the Celsius equivalents. Add the trendline and display the equation. Record the equation of the line. Why is this equation not exactly the same as the second conversion formula (Celsuis from Fahrenheit) given on Slide 10? Why is the value of the intercept 17. 78? Optional activity: Excel can give you a value for one unit from the other unit if you use the built-in TREND function. The format of this function is: =TREND(range of y values, range of x-values, x-value to convert) If you want to determine the Celsius equivalent of 350 degrees Fahrenheit, enter: =TREND(C 4: C 36, B 4: B 36, 350) in any open cell in the spreadsheet. Record the value you obtain. 14

End of Module Assignments Turn in your answers to these questions. 1. Given the following formulae, write the corresponding Excel equations. a. 12 x 2 b. Column B row 3 divided by 56 c. 1. 55 x 106 multiplied by 1. 8 x 10 -3 2. Convert the following numbers to decimal notation and Excel notation. a. 3. 94 x 1012 b. 7. 234 x 10 -4 3. In the country Gogobee, the currency is lemons. There are 62. 9 lemons in a dollar. You want to buy some items. a. If shoes cost 580 lemons, how many dollars do you have to part with to wear them? b. You need bandages for the blisters from your new shoes. They cost $2. 49. How many lemons is this? 4. A perceived advantage of the metric system is that the conversions are based on powers of ten. Explain what this means to you. Do you agree or disagree that the metric system offers advantages? 15

End of Module Assignments 5. You are planning a road trip through Canada, where speed limits are posted in kilometers/hour. You have a lead foot, but don’t want to get stopped for speeding, so you need to get a sense for the relationship between miles/hour (mph) and kilometers/hour. a. In one column of a spreadsheet, create a list of speeds in miles/hour starting with 5 mph and ending with 100 mph in increments of 5. b. In a second column, create and copy a formula to convert miles/hour to kilometers/hour. The relationship between miles and kilometers is 1. 609 kilometers per mile. c. Create an XY scatter graph of these data. Be sure to label the axes. Add the trendline and display the equation of the line on the chart. Print the table and graph and turn them in. 6. Optional question: 2. 17 grams of Na. Cl (table salt) occupies a volume of 1 cubic centimeter (1 cc 3 – a small cube 1 centimeter on each side). What volume in cc 3 is occupied by 60 grams of salt? Would this make French fries salty? Answer this question using a conversion ratio. 7. Optional question: Refer back to the mass spreadsheet. Using the 1 TREND function, determine the milligram equivalent of 2. 5 pounds. 6

Pretest 1. Convert the following numbers to decimal notation and Excel notation. a. 6. 345 x 105 b. 8. 5 x 10 -4 2. What is the relationship between: a. A kilogram and a gram? b. A liter and a milliliter? 3. Convert 55 millimeters to kilometers. 4. How would you write the following mathematical formulae as Excel equations? a. 7. 3 multiplied by the contents of cell column A row 6 b. 5. 2 + 4 + (10 divided by 7) 17