SS 2017 Software Verification Automated Verification Prof Dr

SS 2017 Software Verification Automated Verification Prof. Dr. Holger Schlingloff 1, 2 Dr. Esteban Pavese 1 (1) Institut für Informatik der Humboldt Universität (2) Fraunhofer Institut für offene Kommunikationssysteme FOKUS

Hallo! • Mein Name ist Holger Schlingloff • Ich bin Professor am Institut für Informatik § Themen: Spezifikation, Verifikation & Testtheory • Ich arbeite auch bei der Fraunhofer Gesellschaft § Fraunhofer Institut für Offene Kommunikations. Systeme (FOKUS) • Mehr finden Sie unter … H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 2

Worum geht‘s. . . • Software für sicherheitskritische Systeme § Flugzeuge, Bahnsignalisierung, Airbags, … • Methoden der Verifikation § „automatisierte Korrektheitsbeweise“ • Modellprüfung (Model Checking) • Temporale Logik von Programmen H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 3

Organisatorisches • Ziele: Kenntnisse über den praktischen Einsatz von • Methoden und Werkzeugen zur Software-Verifikation Umfang: 4 SWS VL, 2 SWS Ü VL: Di 11 -13 und Do 9 -11 in Rud 26, 1307 Ü: Di 13 -15, Beginn 2. 5. 2017 9 ECTS-Leistungspunkte = 270 Stunden = 20 Stunden pro Woche Hausaufgaben: Werkzeugeinsatz & praktische Beispiele - eigene Präsentation von Lösungen erforderlich! § Klausur oder mündliche Abschlussprüfung § § • Materialien werden nach der VL verfügbar gemacht § Moodle, Webseite, . . . • Sprache „teilweise Englisch“ H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 4

Welcome to the class! Contents: • Automated verification methods for (embedded) software (and hardware) for safety-critical applications § § § temporal logic: expressivity, complexity model checking: theory and practice verification of real-time systems probabilistic verification software model checking H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 5

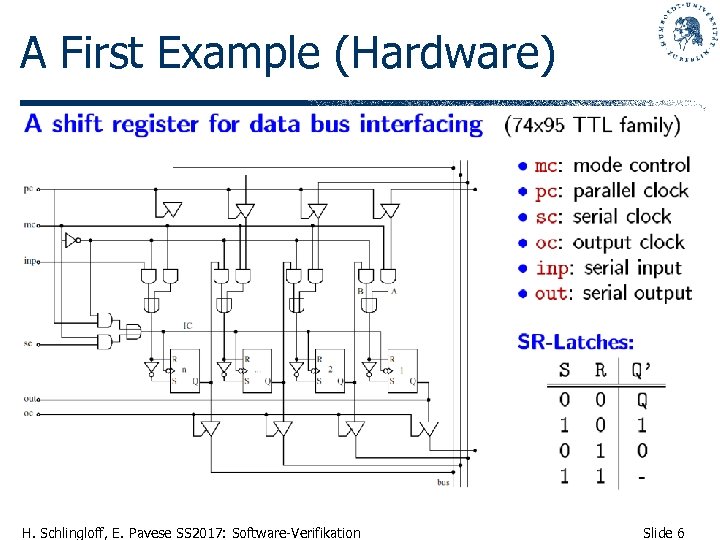A First Example (Hardware) • gibts vielleicht noch besser (color) H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 6

Verification Model of Shift Register H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 7

Correctness Properties • checked for n=32 in less than a second H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 8

Literature • E. M. Clarke, H. Schlingloff: Model Checking. • • • Chapter 21 in Alan Robinson and Andrei Voronkov (eds. ), Handbook of Automated Reasoning; Elsevier Science Publishers B. V. , pp. 1367 - 1522 (2000) E. M. Clarke, O. Grumberg, D. Peled: Model Checking. MIT Press (2000) C. Baier, J. -P. Katoen: Principles of Model Checking. MIT Press (2008) B. Bernard, M. Bidoit, A. Finkel, F. Laroussinie, A. Petit, L. Petrucci, P. Schnoebelen: Systems and Software Verification: Model-Checking Techniques and Tools. Springer (2001, 2010) H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 9

Plan for the Summer • Introduction • Modeling of systems • Temporal logics (LTL, CTL*) • Model checking algorithms • Symbolic representations (BDDs) • Abstraction and refinement (CEGAR) • Real time model checking • Probabilistic model checking H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 10

Short Break! Here was a cartoon which has been removed due to copyright reasons H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 11

Propositional Logic • A formal specification method consists of three parts § syntax, i. e. , what are well-formed specifications § semantics, i. e. , what is the meaning of a specification § calculus, i. e. , what are transformations or deductions of a specification • Propositional logic: probably the first and most widely used specification method § dates back to Aristotle, Chrysippus, Boole, Frege, … § base of most modern logics § fundamental for computer science H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 12

Syntax of Propositional Logic • Let Ρ be a finite set {p 1, …, pn} of propositions and assume that , and (, ) are not in Ρ • Syntax § § PL : : = Ρ | | (PL PL) every p is a wff („falsum“) if and are wffs, then ( ) is a wff nothing else is a wff H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 13

Remarks • Ρ may be empty § still a meaningful logic! • Minimalistic approach § infix-operator necessitates parentheses § other connectives can be defined as usual ¬ ≙ ( ) (linear blowup!) Τ ≙ ¬ ( ) ≙ (¬ ) ( ) ≙ ¬(¬ ¬ ) ≙ ¬( ¬ ) ( ) ≙ (( )) (exponential blowup!) § operator precedence as usual § literal = a proposition or a negated proposition H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 14

Exercise • Abbreviations ¬ ≙ ( ) also ~ Τ ≙ ¬ ( ) ≙ (¬ ) also ( + ), ( | ), ( v ) ( ) ≙ ¬(¬ ¬ ) ≙ ¬( ¬ ) also ( * ), ( & ), ( ^ ) ( ) ≙ (( )) also ( <-> ), ( <=> ) • Write ((p q) ¬p) unabbreviated H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 15

Choice of the Signature • Te set Ρ={p 1, …, pn} of propositions is also called the signature of the logic • The choice of Ρ often is the decisive abstraction step for modelling a system § it determines which aspects are “accessible” to the specification § Wittgenstein: “die Welt ist alles was der Fall ist”; the world consists of all true propositions § e. g. , sun-is-shining, pot-on-stove, line-busy, button_pressed, window 5 infocus, motor-on, … § names should be chosen with consideration H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 16

Semantics of Propositional Logic • Propositional Model § Truth value universe U: {true, false} § Interpretation I: assignment Ρ ↦ U § Model M: (U, I) • Validation relation ⊨ between model M and formula § M ⊨ p if I(p)=true § M⊭ § M ⊨ ( ) if M ⊨ implies M ⊨ • M validates or satisfies iff M ⊨ § is valid (⊨ ) iff every model M validates § is satisfiable (SAT( )) iff some model M satisfies H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 17

Puzzle Example: Ivor Spence’s Sudoku http: //www. cs. qub. ac. uk/~i. spence/Su. Doku. html Slide 18 H. Schlingloff, E. Pavese SS 2017: Software-Verifikation

How Does He Do It? • Propositional modelling § 9 propositions per cell: proposition “ijk” indicates that row i, column j contains value k § individual cell clauses - each cell contains exactly one value Ø (ij 1 v ij 2 v … v ij 9) ^ ~(ij 1 ^ ij 2) ^ … ^ ~(ij 8 ^ ij 9) § row and column clauses - each row i contains each number, exactly once Ø (i 11 v … v i 91) ^ (i 12 v … v i 92) ^ … (i 19 v … v i 99) Ø j 1 j 2, k=1. . 9: ~(ij 1 k ^ ij 2 k) same for columns § block clauses – similar § pre-filled cells – easy • SAT solving § 729 propositions, ca. 3200 clauses few seconds H. Schlingloff, E. Pavese SS 2017: Software-Verifikation Slide 19