Средняя линия треугольника 8 класс ЦЕЛИ УРОКА

Средняя линия треугольника 8 класс

ЦЕЛИ УРОКА: v. Дать определение средней линии треугольника. v. Доказать теорему о средней линии треугольника. v. Решать задачи, используя определение и свойство средней линии.

Определение: Отрезок, соединяющий середины двух сторон треугольника, называют средней линией треугольника.

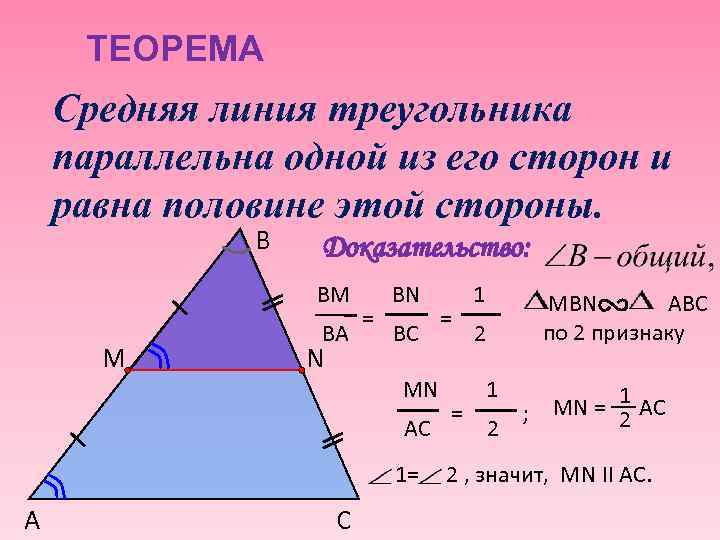ТЕОРЕМА Средняя линия треугольника параллельна одной из его сторон и равна половине этой стороны. B Доказательство: BM М BA N = BN BC MN AC 1= А C = = 1 MBN ABC по 2 признаку 2 1 MN = 1 АС ; 2 2 2 , значит, МN II АС.

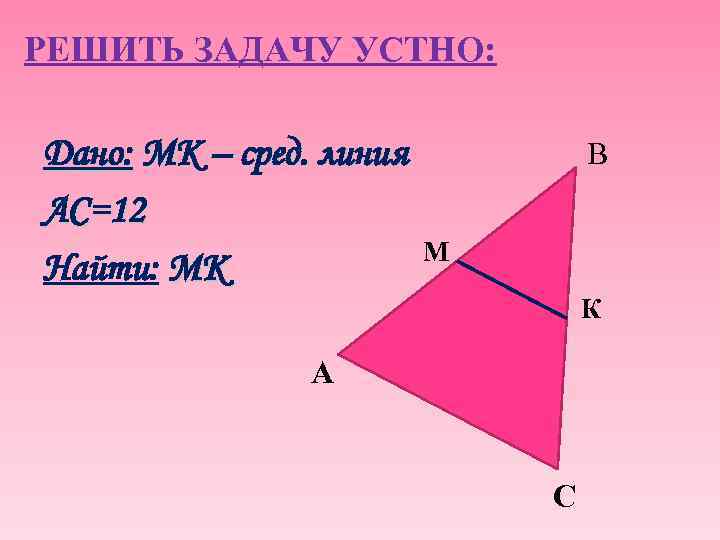РЕШИТЬ ЗАДАЧУ УСТНО: Дано: MК – сред. линия АС=12 Найти: MК В М К А С

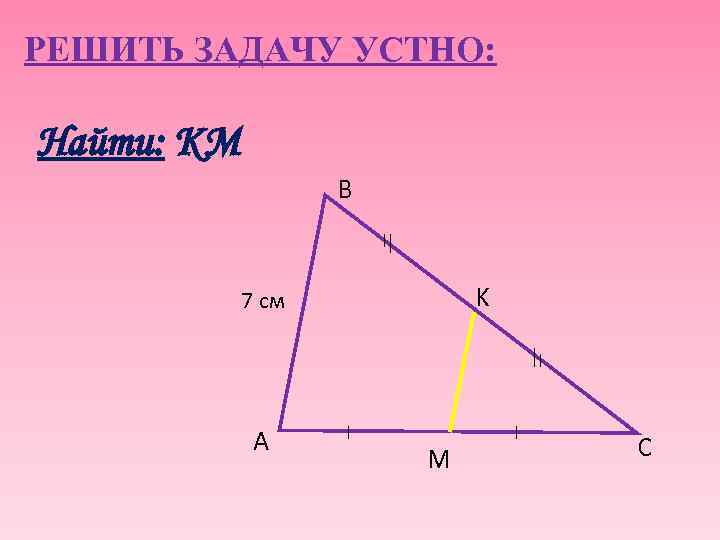РЕШИТЬ ЗАДАЧУ УСТНО: Найти: КМ B K 7 см A M C

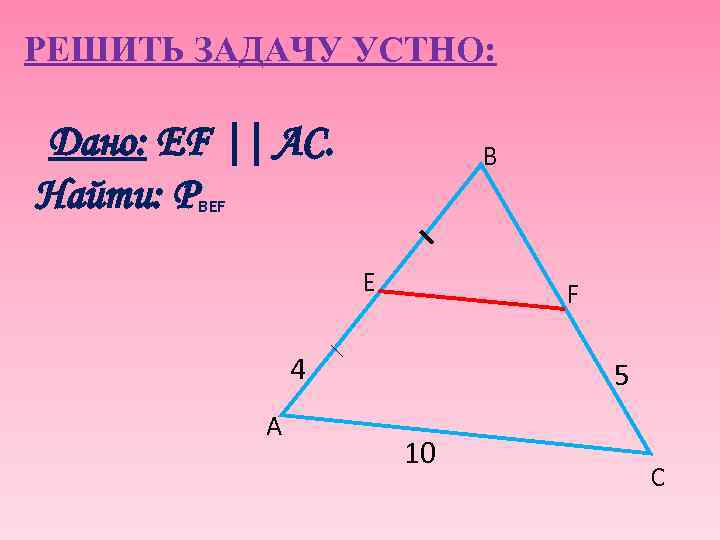РЕШИТЬ ЗАДАЧУ УСТНО: Дано: EF || AC. Найти: Р ВЕF B Е F 4 A 5 10 С

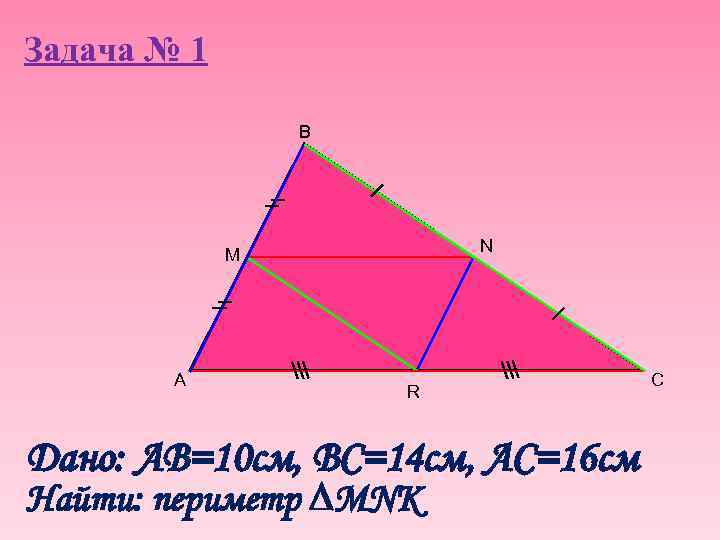Задача № 1 B N M A R Дано: AB=10 cм, ВС=14 см, АС=16 см Найти: периметр MNK C

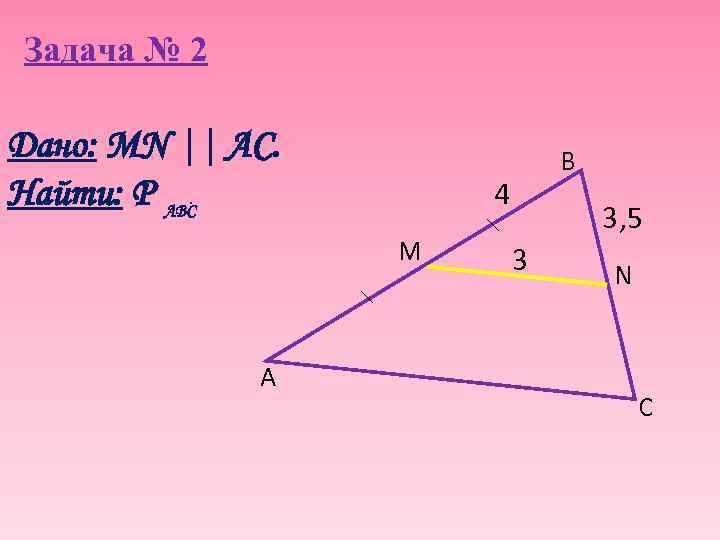Задача № 2 Дано: MN || AC. Найти: Р ABC. 4 M A B 3, 5 3 N C

Задача № 3 Дано: СD║BE║MK; AD =16; CD =10; MB=4 Найти: B C M А D K E

Подведем итог üКакие новые знания получены на уроке? üЧто называют средней линией треугольника? üСформулируйте теорему о средней линии треугольника. üВопросы, которые вы можете задать себе, одноклассникам, учителю.

Домашнее задание: Обязательный уровень: п. 62 (стр. 146), № 570 Дополнительно Составить задачи на готовых чертежах