СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ ПОДГОТОВИЛИ УЧЕНИЦЫ 9 В КЛАССА

СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ ПОДГОТОВИЛИ УЧЕНИЦЫ 9 В КЛАССА ЖИВАЙКИНА ОЛЬГА И КУЗЬМИНА КСЕНИЯ

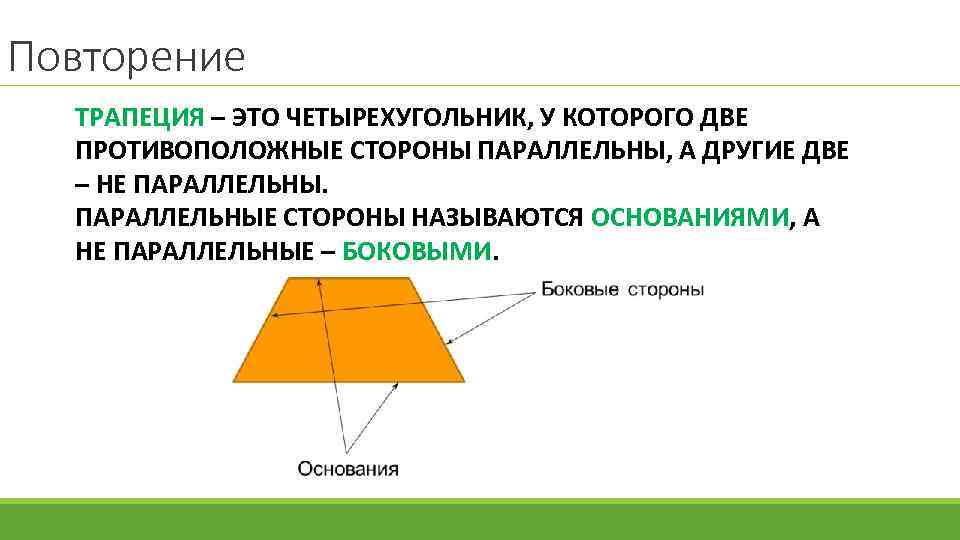Повторение ТРАПЕЦИЯ – ЭТО ЧЕТЫРЕХУГОЛЬНИК, У КОТОРОГО ДВЕ ПРОТИВОПОЛОЖНЫЕ СТОРОНЫ ПАРАЛЛЕЛЬНЫ, А ДРУГИЕ ДВЕ – НЕ ПАРАЛЛЕЛЬНЫЕ СТОРОНЫ НАЗЫВАЮТСЯ ОСНОВАНИЯМИ, А НЕ ПАРАЛЛЕЛЬНЫЕ – БОКОВЫМИ.

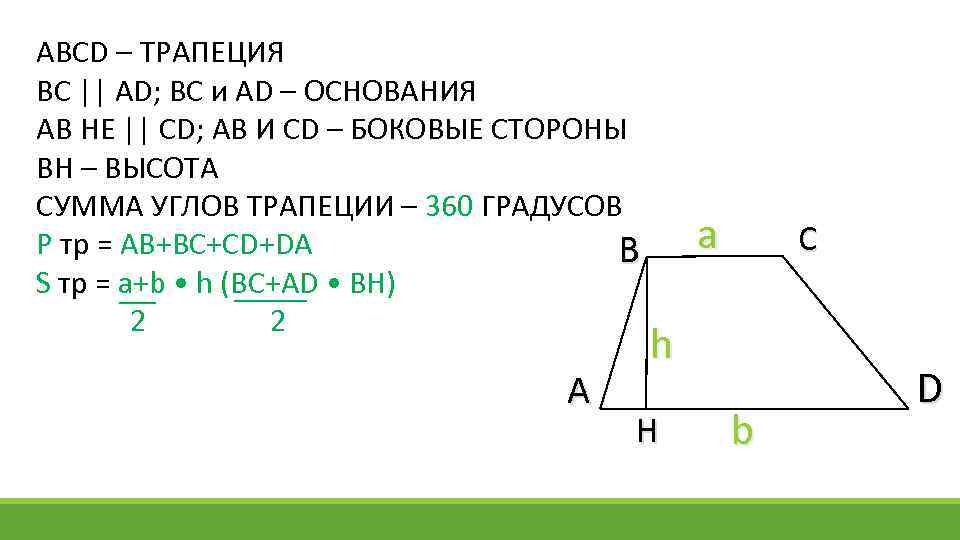ABCD – ТРАПЕЦИЯ BC || AD; BC и AD – ОСНОВАНИЯ AB НЕ || CD; AB И СD – БОКОВЫЕ СТОРОНЫ BH – ВЫСОТА СУММА УГЛОВ ТРАПЕЦИИ – 360 ГРАДУСОВ P тр = AB+BC+CD+DA В S тр = a+b • h (BC+AD • BH) 2 2 А а С h H b D

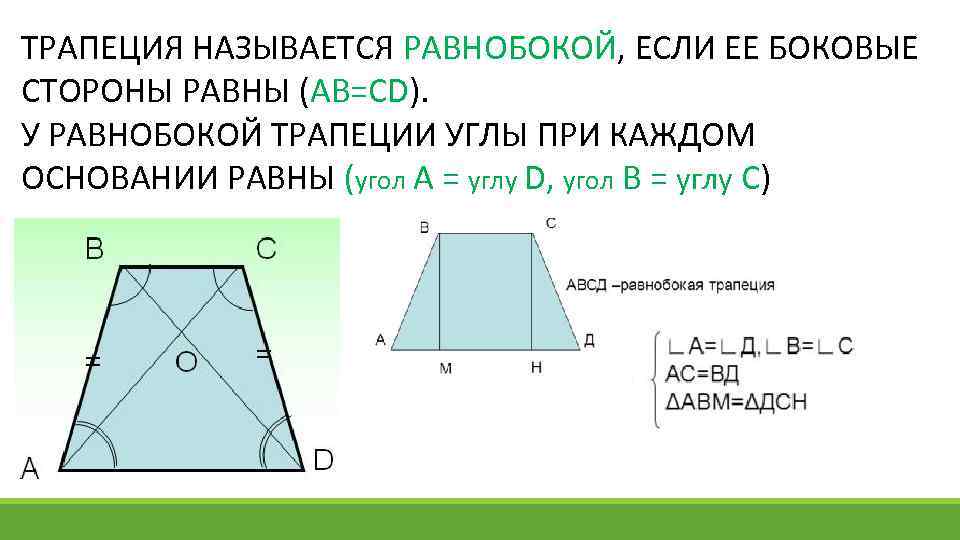ТРАПЕЦИЯ НАЗЫВАЕТСЯ РАВНОБОКОЙ, ЕСЛИ ЕЕ БОКОВЫЕ СТОРОНЫ РАВНЫ (AB=CD). У РАВНОБОКОЙ ТРАПЕЦИИ УГЛЫ ПРИ КАЖДОМ ОСНОВАНИИ РАВНЫ (угол А = углу D, угол B = углу C)

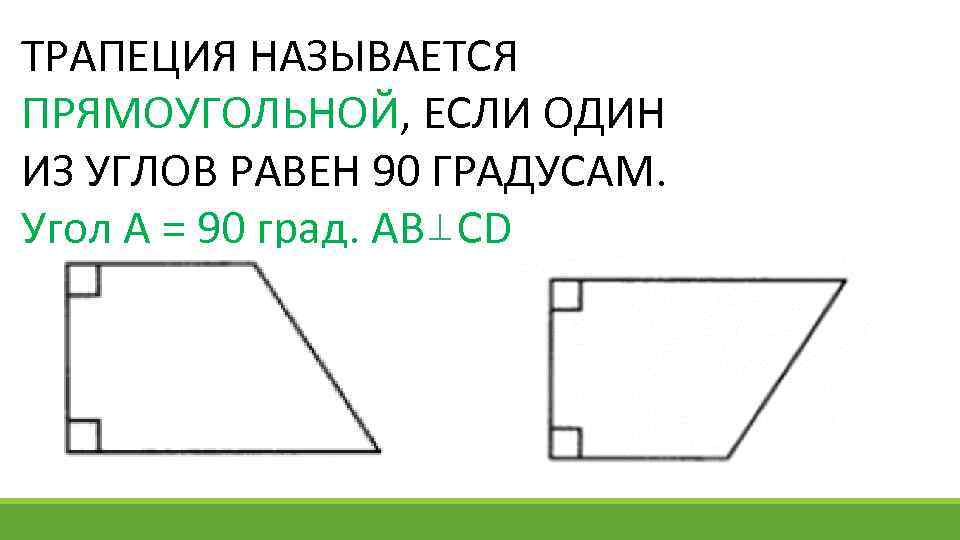ТРАПЕЦИЯ НАЗЫВАЕТСЯ ПРЯМОУГОЛЬНОЙ, ЕСЛИ ОДИН ИЗ УГЛОВ РАВЕН 90 ГРАДУСАМ. Угол A = 90 град. AB CD

СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ - ОТРЕЗОК, СОЕДИНИЮЩИЙ СЕРЕДИНЫ БОКОВЫХ СТОРОН ЭТОЙ ТРАПЕЦИИ (MN – СРЕДНЯЯ ЛИНИЯ, ОНА ПАРАЛЛЕЛЬНА ОСНОВАНИЯМ И РАВНА ИХ ПОЛУСУММЕ) MN – средняя линия MN ||BC||AD MN = BC+AD (a+b) 2 2

ТЕОРЕМА СРЕДНЯЯ ЛИНИЯ ТРАПЕЦИИ ПАРАЛЛЕЛЬНА ОСНОВАНИЯМ И РАВНА ИХ ПОЛУСУММЕ

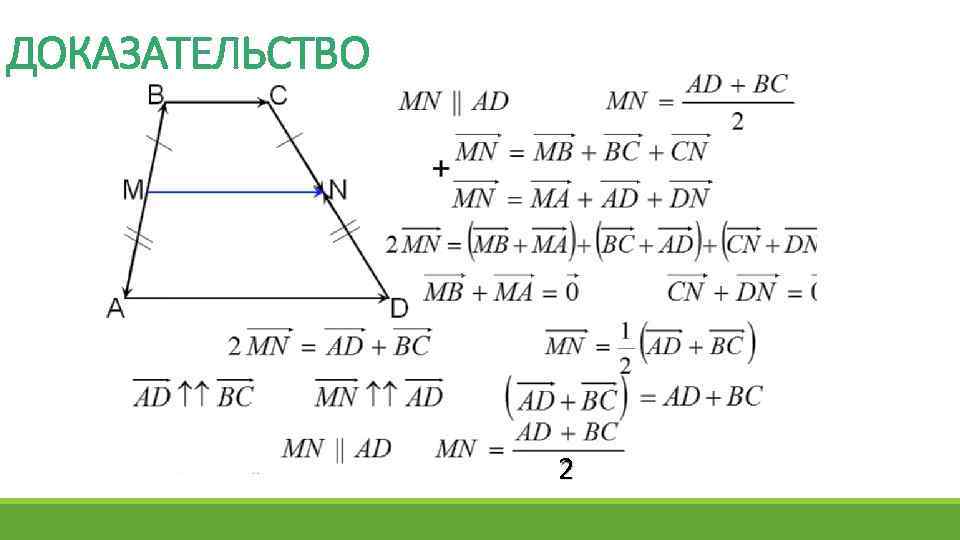ДОКАЗАТЕЛЬСТВО 2