Средние величины Виды средних величин Средняя арифметическая величина

Средние величины Виды средних величин. Средняя арифметическая величина. Другие виды средних величин. Степенные средние. Структурные средние (мода, медиана).

Средняя величина обобщающая характеристика однородной совокупности явлений по определенному признаку Средние величины делятся на две основные категории: n степенные средние; n структурные средние. n

Различные средние выводятся из общей формулы степенной средней: где - величины, для которых исчисляется средняя; - средняя, где черта сверху свидетельствует о том, что имеет место осреднение индивидуальных значений; - частота (повторяемость индивидуальных значений признака k — показатель степени средней.

Средняя арифметическая величина средняя арифметическая простая где хi – индивидуальные значения признака; n – число единиц совокупности. средняя арифметическая взвешенная fi - сколько раз повторятся варианты значения признака (частоты или веса)

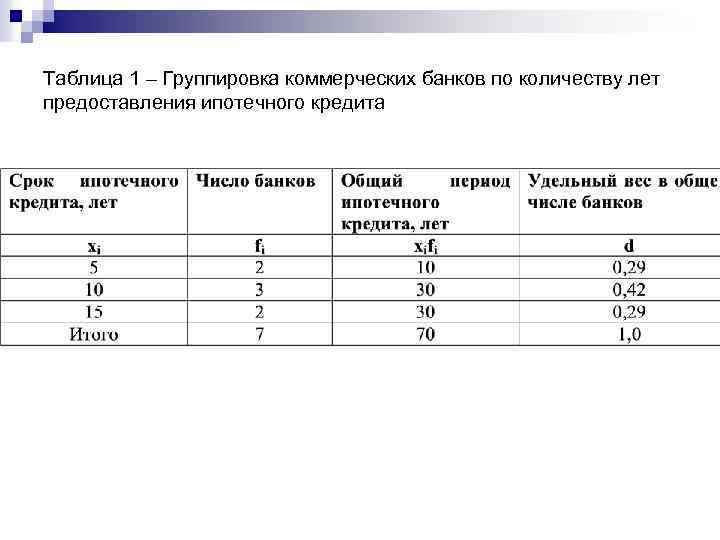Таблица 1 – Группировка коммерческих банков по количеству лет предоставления ипотечного кредита

Если веса представлены в виде относительных величин структуры (в процентах или долях единицы). где доля каждой группы в общем числе единиц совокупности

Вычисление средней арифметической интервального ряда n сначала необходимо определить среднюю для каждого интервала, а затем — для всего ряда.

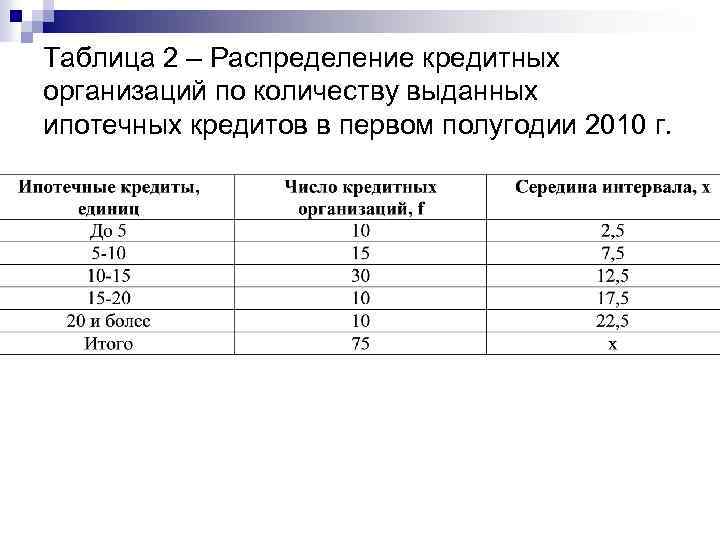Таблица 2 – Распределение кредитных организаций по количеству выданных ипотечных кредитов в первом полугодии 2010 г.

основные свойства средней арифметической: 1. Средняя арифметическая суммы варьирующих величин равна сумме средних арифметических величин Если хi = уi + zi, то

основные свойства средней арифметической: 2. Алгебраическая сумма отклонений индивидуальных значений варьирующего признака от средней равна нулю, так как сумма отклонений в одну сторону погашается суммой отклонений в другую, т. е.

основные свойства средней арифметической: 3. Сумма квадратов отклонений значений признака от средней меньше суммы квадратов отклонений от любой произвольной величины А:

основные свойства средней арифметической: 4. Если все варианты ряда уменьшить или увеличить на одно и то же число а, то средняя уменьшится или увеличится на это же число а:

основные свойства средней арифметической: 5. Если все варианты ряда уменьшить или увеличить в А раз, то средняя также уменьшится или увеличится в А раз.

Другие виды средних величин Простая: n Средняя гармоническая. Простая: n Взвешенная: Средняя геометрическая. Простая: n Взвешенная: Средняя квадратическая. Взвешенная:

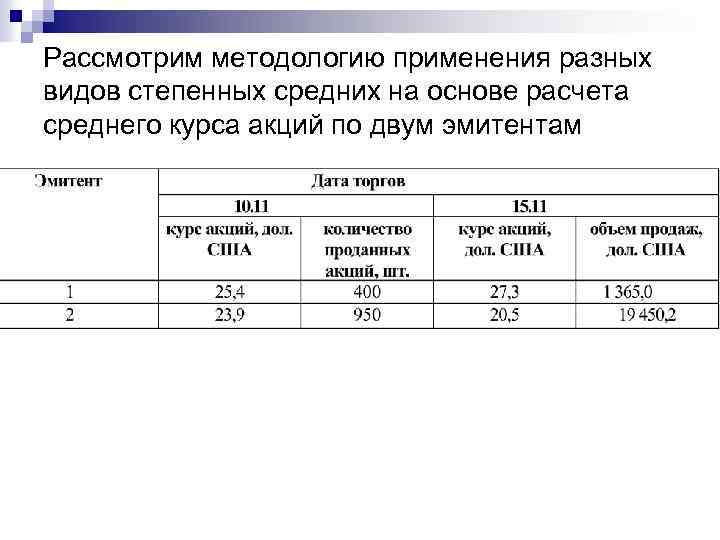Рассмотрим методологию применения разных видов степенных средних на основе расчета среднего курса акций по двум эмитентам

Определим исходное соотношение средней для показателя «средний курс акций» :

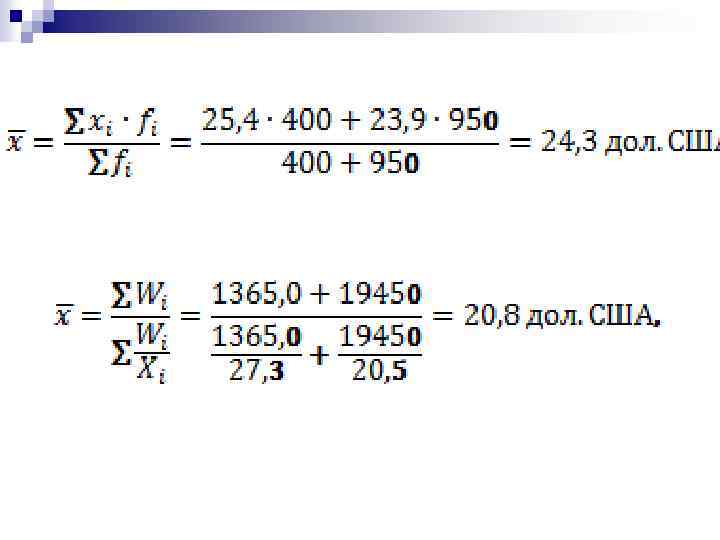
Структурные средние Мода — наиболее часто встречающееся значение ряда. n Медианой является значение элемента, который больше или равен и одновременно меньше или равен половине остальных элементов ряда распределения. Медиана делит ряд на две равные части. n

Расчет моды для интервального вариационного ряда где x 0 – нижняя граница модального интервала; h – величина модального интервала; fm – частота модального интервала fm-1 – частота интервала, предшествующего модальному; fm+1 – частота интервала, следующего за модальным.

Расчет медианы интервального вариационного ряда где х0 — нижняя граница интервала, который содержит медиану; h — величина медианного интервала; — сумма частот или число членов ряда; Sm-1 — сумма накопленных частот интервалов, предшествующих медианному; fm — частота медианного интервала.