Средние величины План 1 Сущность средней в статистике

Средние величины План 1. Сущность средней в статистике. 2. Виды и формы средних величин. 3. Структурные средние.

1. Сущность средней в статистике В результате проведенного статистического наблюдения получают первичный материал, т. е. значения исследуемых признаков для каждой единицы совокупности. Эти значения признаков для конкретных единиц совокупности, как правило, различны. Значение признака отдельных единиц совокупности испытывает вариацию под влиянием множества факторов как основных, так и случайных.

Для того чтобы выявить типичные черты всей совокупности в целом, выявить закономерности, которые присущи массовым явлениям и незаметны в единичных явлениях, необходимо обобщить первичный материал, т. е. рассчитать обобщающие показатели. Наиболее распространенным обобщающим статистическим показателем является средняя величина. Средняя величина – это обобщающая количественная характеристика какого-либо признака в статистической совокупности в конкретных условиях места и времени. Средняя величина выражает типичные черты и показывает степень колеблемости (вариации) признака в однородной совокупности единиц

Средняя величина – это обобщающий показатель, который характеризует типичный уровень варьирующего признака в расчете на единицу совокупности в конкретных условиях места и времени. Средняя величина всегда имеет ту же размерность, что и варьирующий признак. Основным условием правильного научного использования средней величины является качественная однородность совокупности, по которой исчислена средняя. Свойство средней величины – она отражает общее, что присуще всем единицам совокупности.

Сущность средней заключается в том, что в ней взаимопоглощаются отклонения значений признака отдельных единиц совокупности, обусловленные действием случайных факторов, и учитываются изменения, вызванные действием основных факторов. Главное значение средних величин состоит в их обобщающей функции, т. е. Замене множества различных индивидуальных значений признака средней величиной, характеризующей всю совокупность в целом. В силу этого средняя величина отражает типичный уровень признака, абстрагируясь от индивидуальных особенностей отдельных единиц совокупности.

Типичность средней связана с однородностью статистической совокупности. Средняя величина только тогда отражает типичный уровень признака, когда она рассчитывается по качественно однородной совокупности. Под однородностью понимается подчинение всех единиц совокупности одному закону развития в отношении рассматриваемого свойства. Поэтому исчислять среднюю величину нужно в сочетании с методом группировки, т. е. по каждой однородной группе.

Сущность средней можно дать через понятие ее определяющего свойства: средняя, являясь обобщающей характеристикой всей статистической совокупности, должна ориентироваться на определенную величину, связанную со всеми единицами этой совокуп ности. Эту величину можно представить в виде функции: f(x 1, x 2, . . . , xk) Если все x 1, x 2, . . . , xk заменить их средним значением , то значение функции должно остаться прежним: f(x 1, x 2, . . . , xk)=f( , , . . . , )

Определить среднюю можно через ее логическую формулу (исходное соотношение средней – ИСС ): Например:

n n 2. Виды и формы средних величин Основные виды средних величин следующие: - арифметическая средняя; - гармоническая средняя; - геометрическая средняя; - квадратическая средняя, кубическая и. т. д По форме средние величины бывают простые и взвешенные. Кроме рассмотренных выше видов средних величин существует также структурные (ранговые) средние, среди которых наиболее распространены мода и медиана. В исследовании динамических рядов используются различные формы средней хронологической.

1)Средняя арифметическая величина Средней арифметической величиной n называется такое значение признака в расчете на единицу совокупности, при вычислении которого общий объем признака в совокупности остается неизменным. Средняя арифметическая величина – это среднее слагаемое. При ее вычислении общий объем признака распределяется поровну между всеми единицами совокупности. Исходя из определения, формула средней арифметической простой имеет вид:

Этот вид арифметической средней используется в тех случаях, когда расчет осуществляется по первичным данным индивидуальных значений признака и называется простой арифметической средней. Пример: Средний стаж работы 10 рабочих: X 1 – 3 X 2 – 2 X 3 – 4 X 4 – 3 X 5 – 4 X 6 – 1 X 7 – 4 X 8 – 5 X 9 – 4 X 10 – 6

Воспользуемся следующим исходным соотношением средней Тогда

При расчете средних величин отдельные значения осредняемого признака могут повторяться. Тогда расчет средней производится по сгруппированным данным или вариационным рядам, которые могут быть дискретными или интервальными. В этом случае используется средняя арифметическая взвешенная, формула которой имеет вид:

Упорядочим по возрастанию стажа данные вышерассмотренного примера: Х 6 Х 2 Х 1 Х 4 Х 3 Х 5 Х 7 Х 9 Х 8 Х 10 1 2 3 3 4 4 5 6 Стаж, лет Число рабочих, чел. 1 1 2 1 3 2 4 4 5 1 6 1

Подставляя значения xi и fi в формулу, получим: При расчете средней величины по интервальному вариационному ряду необходимо перейти от интервалов к их серединам.

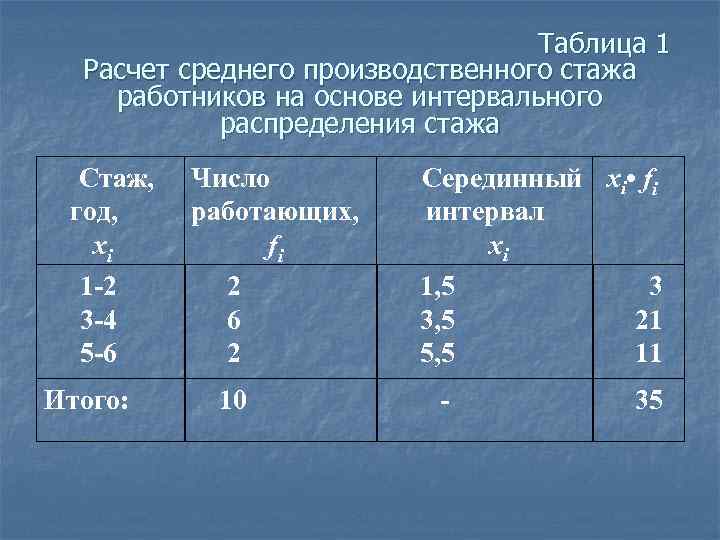Таблица 1 Расчет среднего производственного стажа работников на основе интервального распределения стажа Стаж, год, xi 1 -2 3 -4 5 -6 Итого: Число работающих, fi 2 6 2 10 Серединный xi • fi интервал xi 1, 5 3 3, 5 21 5, 5 11 - 35

Подставляя значения xi и fi в формулу, получим: Средняя величина, полученная для интервального ряда, т. е. взвешенная средняя отличается от простой средней ввиду того, что в расчетах осуществляется осреднение вариантов в интервале и в результате не учитываются реальные индивидуальные значения признаков.

Основные свойства средней арифметической величины: 4) сумма отклонений индивидуального значения признака от средней арифметической равна нулю, т. е.

2) Средняя гармоническая величина Если по условию задачи необходимо, чтобы при осреднении неизменной оставалась сумма величин, обратных индивидуальным значениям признака, то средняя величина является гармонической средней. Для определения средней арифметической величины необходимо иметь значения вариант xi и частот fi

В тех случаях, когда при вычислении средней величины имеются данные об индивидуальных значениях признака х и его общем объеме в совокупности W=xf, но исходная информация не содержит сведений о частотах f, тогда суммированию подлежат не сами варианты, а обратные им величины. Для расчетов применяется формула средней гармонической взвешенной. Здесь wi=xi*fi

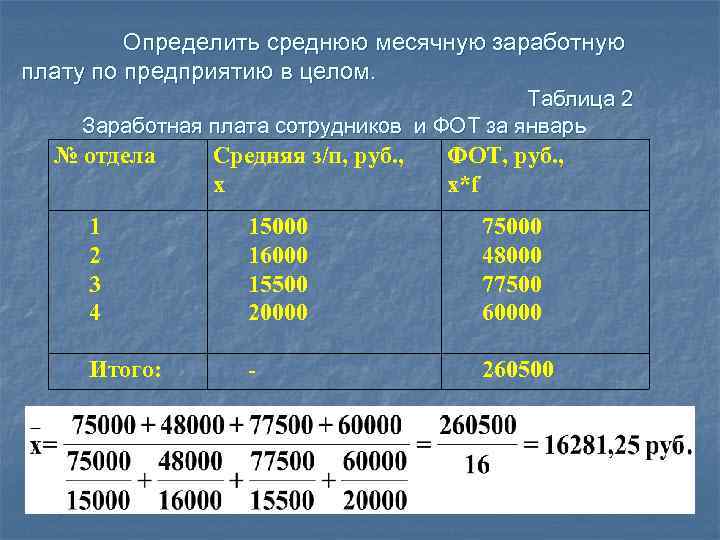Определить среднюю месячную заработную плату по предприятию в целом. Таблица 2 Заработная плата сотрудников и ФОТ за январь № отдела Средняя з/п, руб. , x ФОТ, руб. , х*f 1 2 3 4 15000 16000 15500 20000 75000 48000 77500 60000 Итого: - 260500

3) Средняя геометрическая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменным произведение индивидуальных величин, то следует использовать геометрическую среднюю величину. Для ее расчета применяются следующие формулы. Для простой геометрической средней: Для взвешенной геометрической средней:

4) Средняя квадратическая. Если при замене индивидуальных величин признака на среднюю величину необходимо сохранить неизменной сумму квадратов исходных величин, то следует использовать квадратическую среднюю величину. Для простой Для взвешенной

3. Структурные средние. Особым видом средних величин являются структурные средние. Они применяются для изучения внутреннего строения и структуры рядов распределения значений признака. В качестве таких СС наиболее часто используются: мода (Мо) и медиана (Ме). В отличии от ранее рассмотренных видов средних величин структурные средние характеризуют величину варианта, занимающего определенное положение в ранжированном вариационном ряду. Мода – это такая величина изучаемого признака, которая в данной совокупности встречается наиболее часто, т. е. повторяется с наибольшей частотой.

Для дискретного ряда хj, чел. 0 1 2 3 4 5 6 Итого fj 6 28 22 20 15 7 2 100 xj*fj 0 28 44 60 60 35 12 239 Рассчитаем среднее значение

Если ряд интервальный, то для вычисления Мо сначала находят модальный интервал т. е. интервал, где fi - max. В интервальном вариационном ряду модой приближенно считается центральное значение модального интервала. Более точно моду можно определить графическим методом по гистограмме ряда.

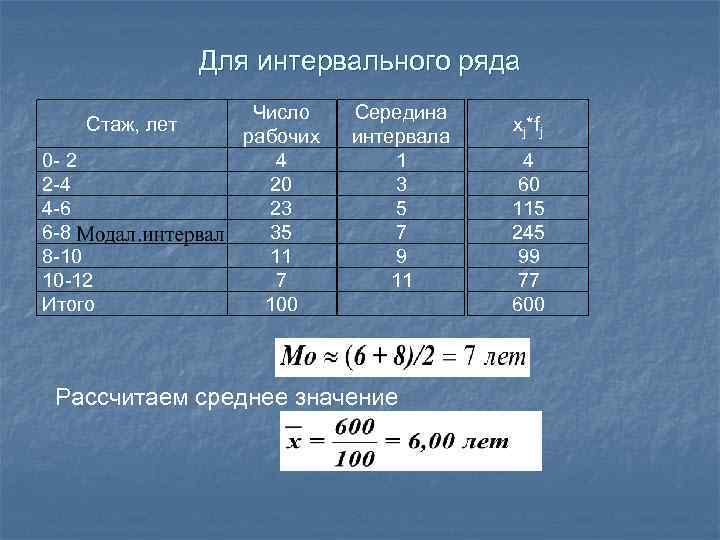Для интервального ряда Стаж, лет 0 - 2 2 -4 4 -6 6 -8 8 -10 10 -12 Итого Число рабочих 4 20 23 35 11 7 100 Середина интервала 1 3 5 7 9 11 Рассчитаем среднее значение xj*fj 4 60 115 245 99 77 600

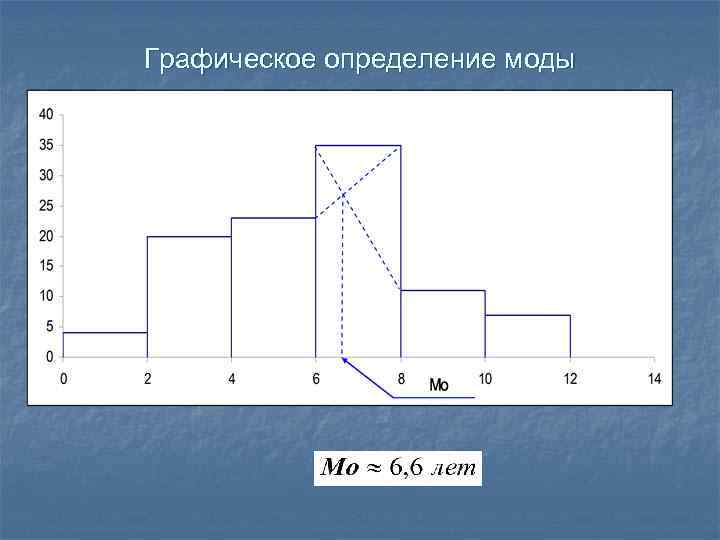Графическое определение моды

Конкретное значение моды для интервального ряда рассчитывается по формуле: где х. Мo – нижняя граница модального интервала, h –величина модального интервала, f. Mo – частота модального интервала, f. Mo-1 – частота интервала, предшествующего модальному, f. Mo+1 – частота интервала, следующего за модальным.

Конкретное значение моды, рассчитанное по формуле равно: Ранее было рассчитано среднее значении

Медиана Ме – это значение признака, приходящееся на середину ранжированного ряда. Если дискретный ряд имеет нечетное число единиц, то Ме - серединный признак в ранжированном ряду. Например, имеем ряд: 4 6 2 3 2 6 5 Сначала ранжируем: 2 2 3 4 5 6 6 Затем находим середину ряда: Ме = 4 Для ранжированного дискретного ряда с четным числом единиц Ме вычисляется как средняя арифметическая из 2 -х смежных серединных значений признака. Например, имеем ряд: 2 2 3 4 5 6 6 7

Для сгруппированных данных сначала определяют положение медианы в ряду по ее номеру Затем необходимо определить медианный интервал, для чего используются накопленные частоты (или частости). Так как медиана делит численность ряда пополам, она будет находиться в том интервале, где накопленная частота впервые превышает полусумму всех частот:

Для дискретного сгруппированного ряда xj 0 1 2 3 4 5 6 Итого fj 6 28 22 20 15 7 2 100 Si 6 34 56 76 91 98 100

Для интервального ряда Стаж, лет Число рабочих SМе 0 - 2 4 4 2 -4 23 27 4 -6 20 47 6 -8 35 82 8 -10 11 93 10 -12 7 100 Итого 100 Медианный интервал 6 – 8 За первое приближенное значение медианы можно взять центральное значение медианного интервала (Ме=7). Более точно моду можно определить графическим методом по кумулятивной кривой

Определение медианы графическим методом Ме Ме ≈ 6, 1 лет

Конкретное значение медианы для. интервального ряда рассчитывается по формуле: где х. Ме– нижняя граница медианного интервала, h – величина медианного интервала, – сумма всех частот, f. Ме – частота медианного интервала, SMе-1 – накопленная частота интервала, предшествующего медианному

Для рассмотренного выше примера: Кроме моды и медианы к структурным средним относятся градиенты: квартили, квинтили, децили, перцентили и др. Квартили – значение признака, делящие ранжированную совокупность на четыре равные части. Для расчета квартилей по интервальному ряду используются формулы: формулы

где: - нижняя граница интервала, содержащего нижний квартиль (интервал определяется по накопленной частоте, первой превышающей 25%); - - нижняя граница интервала, содержащего верхний квартиль (интервал определяется по накопленной частоте, первой превышающей 75%); h - величина интервала; интервала

- накопленная частота интервала, предшествующего интервалу, содержащему нижний квартиль; - накопленная частота интервала, предшествующего интервалу, содержащему верхний квартиль; - частота интервала, содержащего нижний квартиль; - частота интервала, содержащего верхний квартиль.

Распределение коммерческих банков по сроку функционирования Группа банков по сроку Число банков, Накопленная функционирования, лет % к итогу частоcтmm х f 1 -2 10 10 2 -3 15 25 3 -4 21 46 4 -5 25 71 5 -6 12 83 6 -7 7 90 7 -8 5 95 Свыше 8 5 100 Итого 100 -

Q 1 находится в интервале 3 - 4, Q 3 находится в интервале 5 - 6.