Средние величины и показатели вариации Тема урока Средняя

Средние величины и показатели вариации Тема урока: «Средняя величина, сущность, определение, виды. Средняя арифметическая и ее свойства. Понятие о структурных средних» .

Понятие средней величины Средняя величина – обобщенная количественная характеристика признака в статистической совокупности Средняя величина отражает то общее, что присуще всем единицам исследуемой совокупности; поглощает случайные факторы и учитывает изменения, вызванные действием основных факторов; Отражает типичный уровень признака, если она рассчитана по качественно однородной совокупности

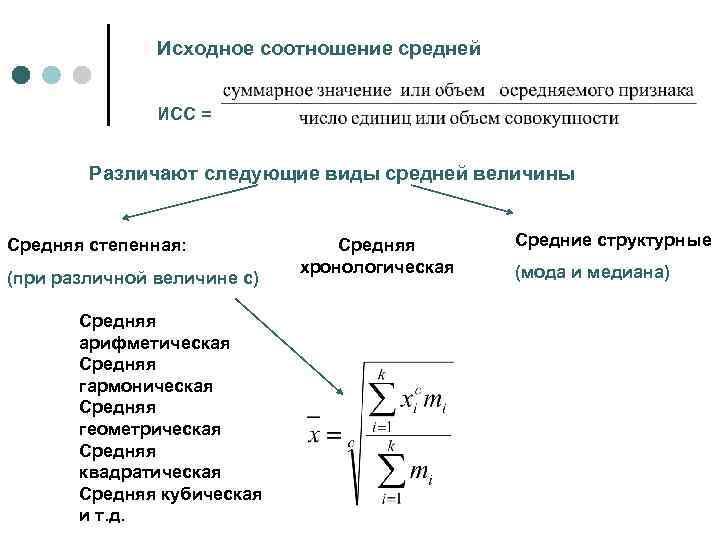Исходное соотношение средней ИСС = Различают следующие виды средней величины Средняя степенная: (при различной величине с) Средняя арифметическая Средняя гармоническая Средняя геометрическая Средняя квадратическая Средняя кубическая и т. д. Средняя хронологическая Средние структурные (мода и медиана)

Средняя арифметическая и ее свойства Средняя арифметическая простая – расчет по несгруппированным данным Средняя арифметическая взвешенная – расчет по сгруппированным данным или вариационным рядам (дискретным, интервальным)

Свойства средней арифметической 1. Произведение средней на сумму частот равно сумме произведений отдельных вариантов на соответствующие частоты 2. Сумма отклонений индивидуальных значений признака от средней арифметической равна нулю

Свойства средней арифметической 3. Сумма квадратов отклонений индивидуальных значений признака от средней арифметической меньше, чем сумма квадратов их отклонений от любой другой произвольной С 4. Если все средние варианты уменьшить или увеличить на постоянное число А, то средняя арифметическая уменьшится или увеличится на ту же величину 5. Если все варианты значений признака изменится в А раз, то средняя так же изменится в А раз

Другие виды средних показателей Средняя гармоническая взвешенная. Данная форма используется, когда известен числитель исходного соотношения средней, но не известен его знаменатель Средняя гармоническая невзвешенная. Данная форма используется, вместо взвешенной, когда wi для единиц совокупности равны

Средняя геометрическая Невзвешенная средняя геометрическая Взвешенная средняя геометрическая Применяется в анализе динамики для определения среднего темпа роста

Структурные средние Мода - значение изучаемого признака, повторяющееся с наибольшей частотой ¢ Медиана – значение признака приходящееся на середину упорядоченной совокупности Несгруппированные данные Пример: 9 торговых фирм города реализуют товар А следующим ценам: 122, 3; 117, 4; 122, 3; 121, 3; 117, 4; 122, 2; 123, 3; 122, 3; 114, 7. Определить моду и медиану предложенного ряда. ¢

Определение моды и медианы по сгруппированным данным (дискретный вариационный ряд) Рост студенток Количество студенток 156 158 160 161 166 168 172 176 4 6 12 8 10 14 13 7

Определение моды и медианы по интервальным рядам x 0 – нижняя граница модального интервала h – ширина модального интервала m. M 0 - частота модального интервала x 0 – нижняя граница медианного интервала, h – ширина медианного интервала, - накопленная частота интервала, предшествующего медианному, mi – частота итого интервала

Показатели вариации Позволяют учитывать вариацию значений отдельных единиц относительно средней. Показатели, характеризующие вариацию: • Размах – разность максимального и минимального значения признака R=xmax-xmin • Дисперсия • Среднее квадратическое отклонение • Коэффициент вариации

Дисперсия Средний квадрат отклонений значений признака от их средней величины Невзвешенная формула Взвешенная формула – используется в тех случаях, когда варианты значений изучаемого признака повторяются

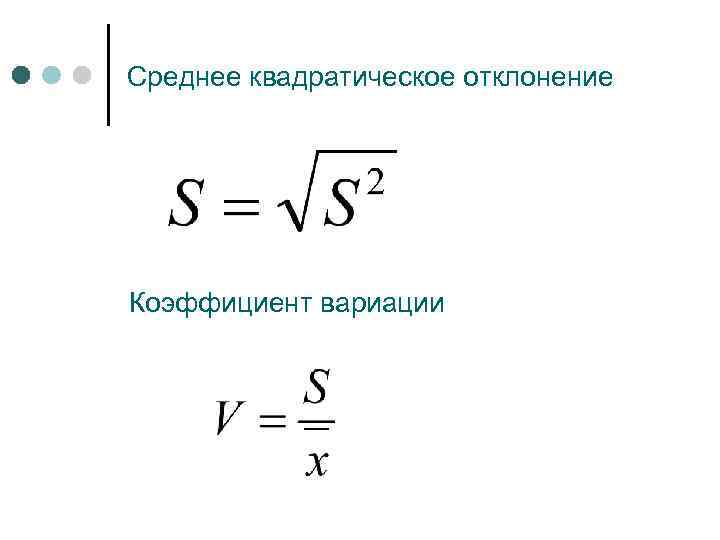Среднее квадратическое отклонение Коэффициент вариации