Средние величины и их применение в правовой статистике

Средние величины и их применение в правовой статистике 1. Понятие средних величин. 2. Виды средних величин и способы их вычисления. 3. Показатели вариации признака.

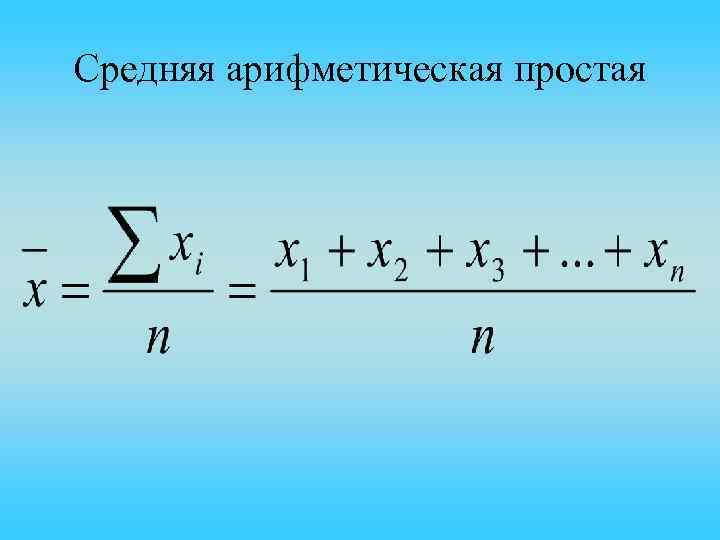Средняя арифметическая простая

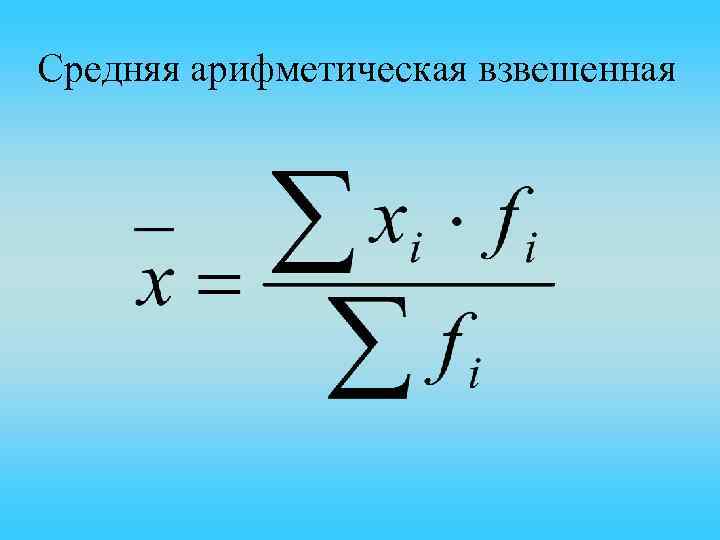Средняя арифметическая взвешенная

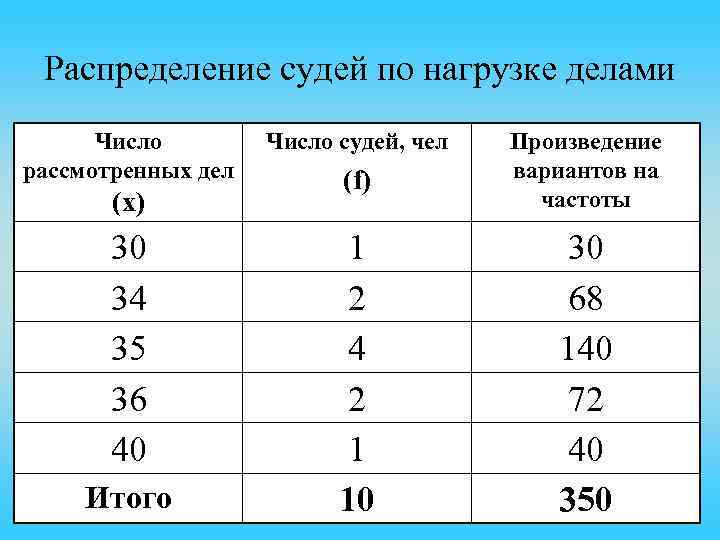Распределение судей по нагрузке делами Число рассмотренных дел (x) 30 34 35 36 40 Итого Число судей, чел (f) Произведение вариантов на частоты 1 2 4 2 1 10 30 68 140 72 40 350

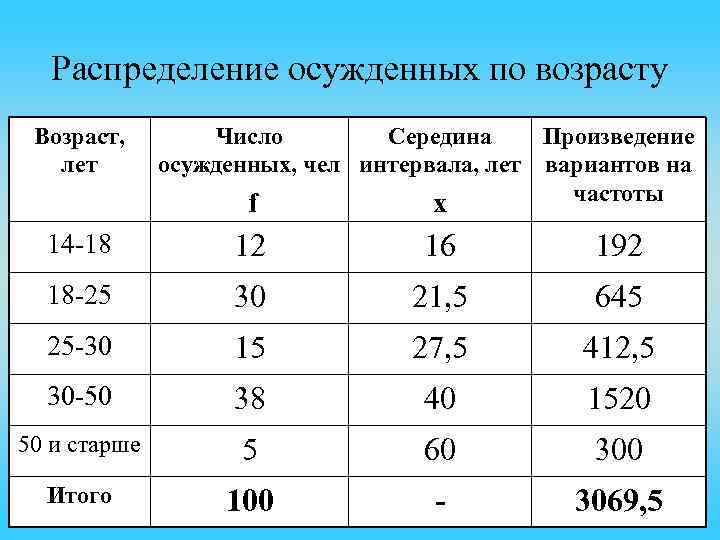Распределение осужденных по возрасту Возраст, лет Число Середина Произведение осужденных, чел интервала, лет вариантов на частоты f x 14 -18 12 16 192 18 -25 30 21, 5 645 25 -30 15 27, 5 412, 5 30 -50 38 40 1520 50 и старше 5 60 300 Итого 100 - 3069, 5

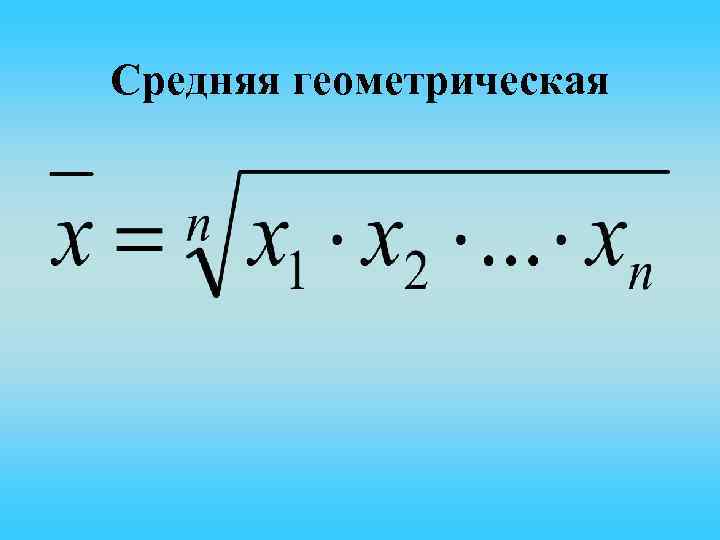Средняя геометрическая

Средняя хронологическая

Мода (Мо) – значение признака (вариант), встречающееся с наибольшей вероятностью в совокупности или в вариационном ряду.

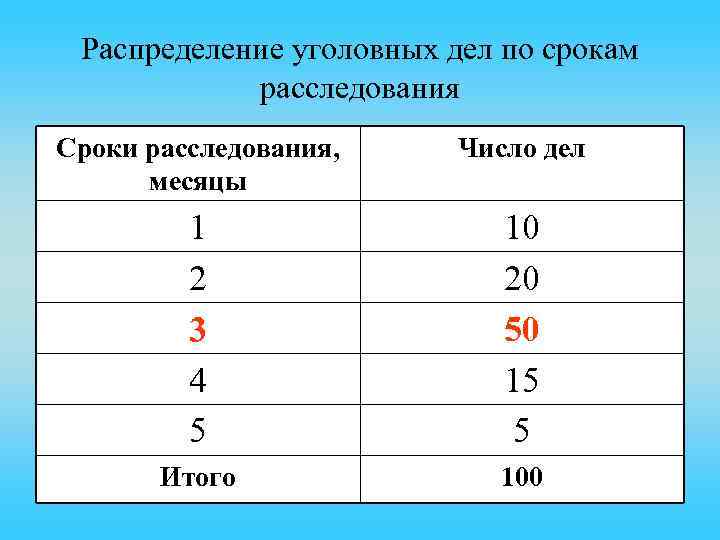Распределение уголовных дел по срокам расследования Сроки расследования, месяцы Число дел 1 2 3 4 5 10 20 50 15 5 Итого 100

Медиана (Ме) – вариант, который находится в середине ранжированного (упорядоченного) ряда, расположенного в определенном порядке – по возрастанию или по убыванию вариантов.

№ осужденного 1 2 3 4 5 6 7 8 9 10 11 Срок лишения свободы, лет 1 1, 5 2 2 2, 5 3 3, 5 4 5 6 6

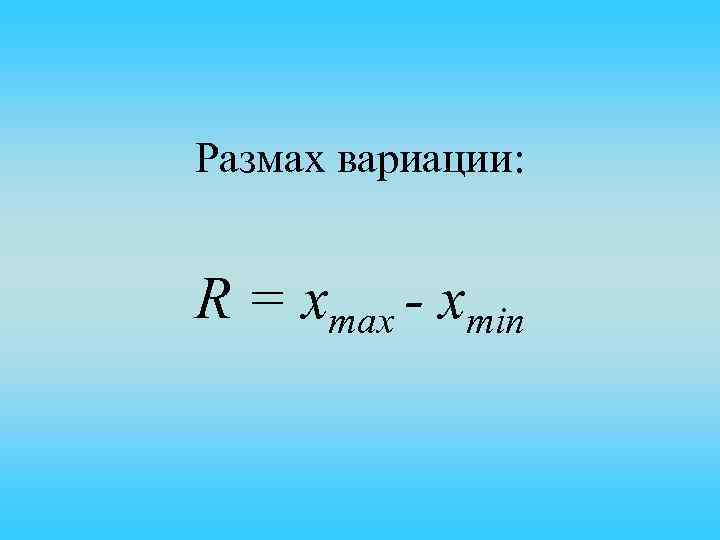Размах вариации: R = xmax - xmin

Среднее линейное отклонение ( ) представляет собой сумму взвешенных по частоте отклонений отдельных значений признака (по абсолютной величине) от их средней арифметической

Дисперсия признака ( ) – средний квадрат отклонений отдельных значений признака от их средней величины.

Среднее квадратическое отклонение ( ) равно корню квадратному из дисперсии и показывает: насколько в среднем отклоняются конкретные значения признака от их средней величины.

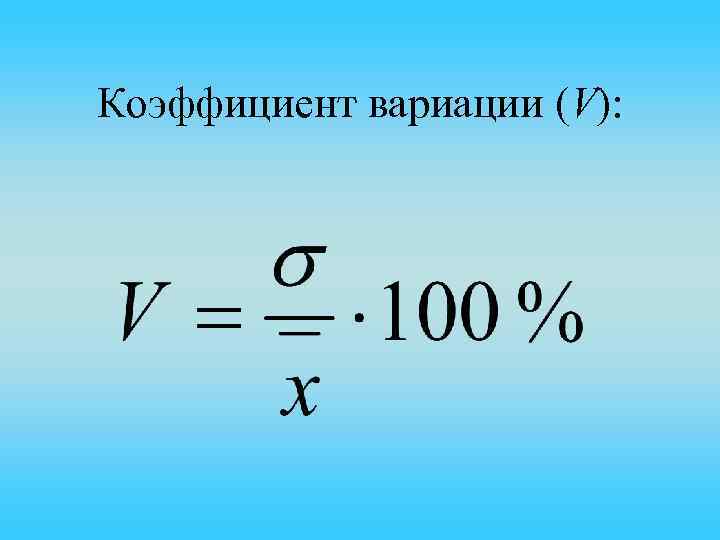Коэффициент вариации (V):