Средние в статистике Степенные средние Структурные средние Средние

Средние в статистике Степенные средние Структурные средние Средние для качественных признаков Хронологические средние

Степенные средние • Общая формула для степенных средних - простая степенная: - взвешенная степенная: m - показатель степени средней n - общее число показателей f i - частота вариантов значений или вес

Степенные средние m = 1 средняя арифметическая простая и взвешенная m = 2 средняя квадратическая простая и взвешенная

Степенные средние • m = 0 средняя геометрическая • m = -1 средняя гармоническая простая и взвешенная • «Мажорантность» степенных средних

Структурные средние Варианты значений Х i 2 3 4 5 Всего Частота f i 3 7 11 3 24 Кумулята частоты F i 3 10 21 24 - Мода - наиболее часто встречаемое значение: Мо = 4 Медиана – значение, делящее всю совокупность на две, равные по численности, части: Ме = 4 Квартили – значения, делящие совокупность на четыре, равные по численности, части: Q 1 = 3; Q 3 = 4 Децили D 1 = 2; D 9 = 5

Структурные средние • Мода • Медиана • Квартили • Децили

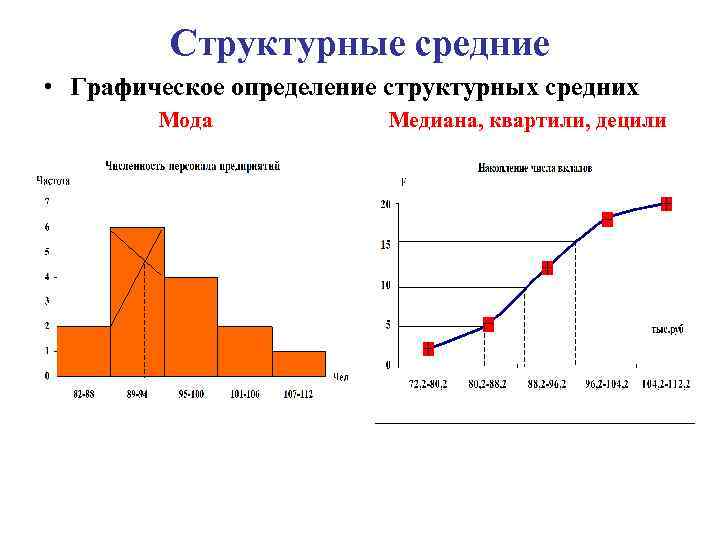Структурные средние • Графическое определение структурных средних Мода Медиана, квартили, децили

Средние для качественных признаков • Все варианты значений качественного признака приведены к двум (альтернативным) вариантам x 1 = 1 – значение ожидаемого значения признака х2 = 0 – значение прочих вариантов признака f 1 = p - доля ожидаемого варианта f 2 = q - доля или удельный вес прочих вариантов p+q=1

Средние хронологические для рядов динамики • средняя хронологическая простая: • средняя хронологическая взвешенная: