4 Сравнительные статистики.pptx
- Количество слайдов: 47

Сравнительные статистики Лекция для студентов 1 курса лечебного факультета Дисциплина доказательная медицина Заведующий кафедрой общественного здоровья и здравоохранения Шульмин А. В.

Цель лекции • Получение информации о способах и методах сравнения количественных и качественных учетных признаков • Научится трактовать медицинские сообщения в части сравнительных статистик

План лекции • 1. Понятие о сравнительной статистике. • 2. Ознакомление с основными параметрическими и непараметрическими критериями значимости различий между переменными. • 3. Определение статистической значимости различий для двух независимых и связанных выборочных совокупностей. 4 4. Понятие о дисперсионном анализе.
Для чего нужны сравнительные статистики?

Для чего нужны сравнительные статистики?

Проверка статистических гипотез Статистической гипотезой называют, гипотезу о видах неизвестного распределения или о параметрах известного распределения. Проверка статистической гипотезы заключается в сопоставлении некоторых статистических показателей, вычисленным по данным выборки со значениями этих же показателей, определенными теоретически в предположении, что проверяемая гипотеза верна. В результате проверки могут быть приняты два неправильных решения, т. е. допущены ошибки двух родов. Ошибка первого рода состоит в том, что будет отвергнута правильная гипотеза. Ошибка второго рода состоит в том, что будет принята неправильная гипотеза. Вероятность совершить ошибку первого рода принято обозначать α. На практике, наиболее часто используют α=0, 05, это означает, что в 5 случаях из 100 имеется риск допустить ошибку первого рода, т. е. отвергнуть правильную гипотезу.

Классификация гипотез n n Статистические, нестатистические Выдвинутая, конкурирующая. Выдвинутую гипотезу называют нулевой (основной) и обозначают Н 0. Конкурирующая гипотеза Н 1 – это гипотеза альтернативная нулевой, т. е. противоречащая основной. По количеству предположений: простые, сложные. Простая – это гипотеза содержащая только одно предположение. Сложная – гипотеза состоящая из конечного или бесконечного числа простых гипотез.

Статистический критерий, статистическая область Для проверки Н 0, используют специально подобранную случайную величину, точное или приближенное значение которой известно. Эту величину обозначают через U или Z, если она распределена нормально; F или υ² - по закону Фишера; χ² - по закону «хи квадрат» ; Т или t - по распределению Стьюдента. Статистическим критерием называют случайную величину служащую для проверки Н 0. Наблюдаемым значением критерия называют, значение критерия выраженное по данным выборки. После выбора определенного критерия, множество всех его возможных значений разбивается на два подмножества: n содержит значения критерия при котором Н 0 отвергается; n содержит значения критериев при которых Н 0 принимается.

Критической областью называют, совокупность значений критерия при которых Н 0 отвергается. Областью принятия гипотезы (областью допустимых значений), называют совокупность критерия при которой Н 0 принимают. Основной принцип проверки статистических гипотез: если наблюдаемое значение критерия принадлежит критической области, то гипотезу отвергают; если наблюдаемое значение критерия принадлежит области покрытия гипотезы, то гипотезу принимают. Критическая область и область покрытия гипотез – это интервалы, следовательно существует точка которая их разделяет. Критической точкой (границей), называют точку определяющую критическую область от области принятия гипотез. 1. Одностостороннюю критическую область n левостороннюю n правостороннюю 2. Двустороннюю критическую область

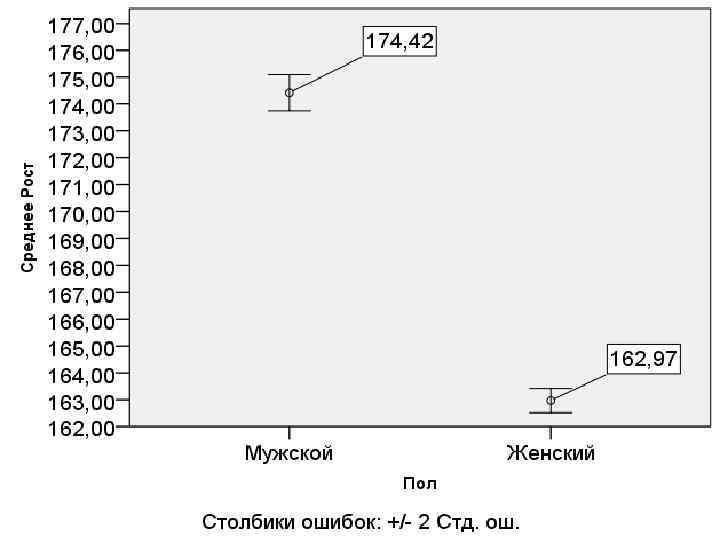
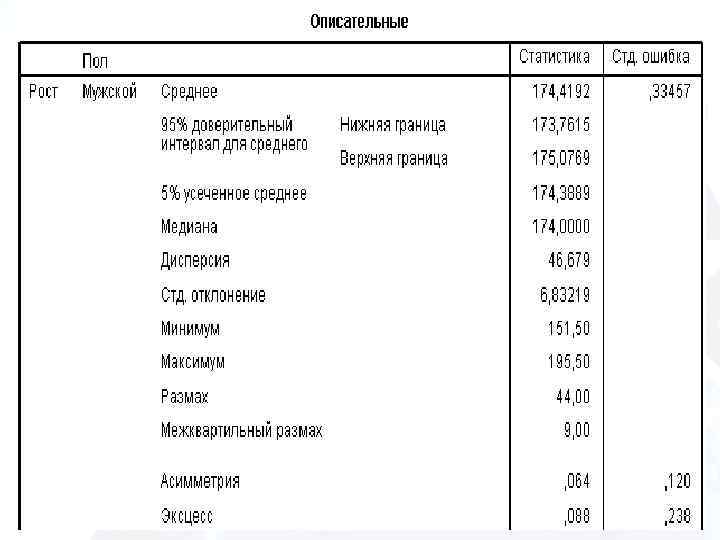
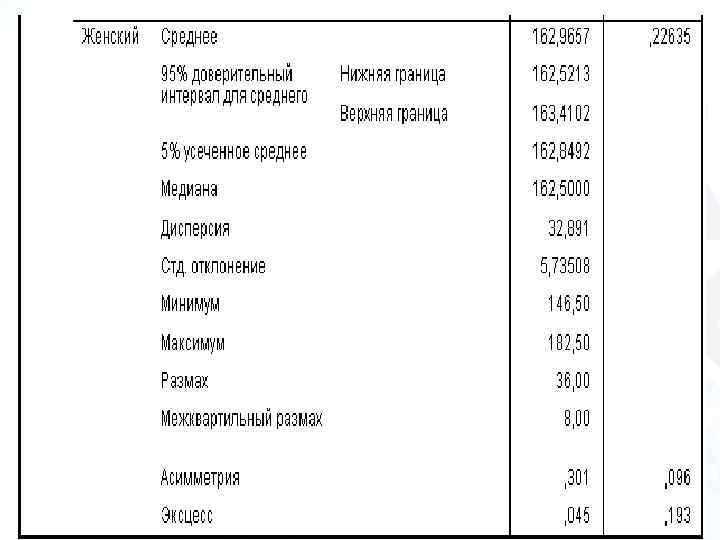
Рост студентов Высота (V или Х) Частота (Р)
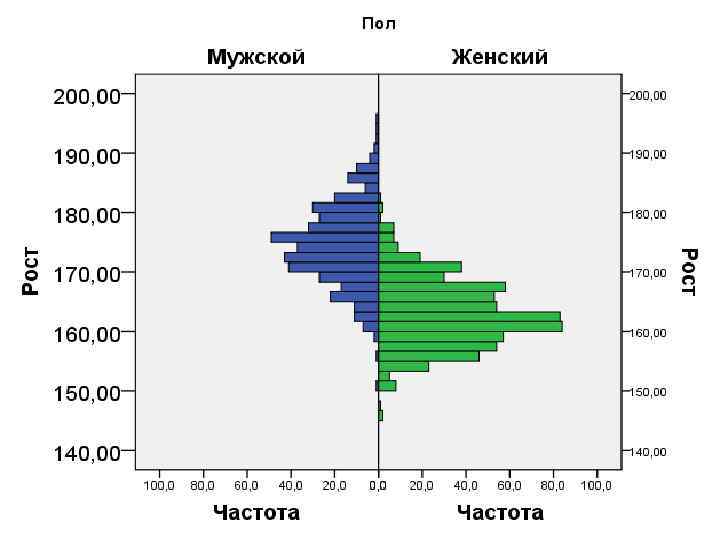
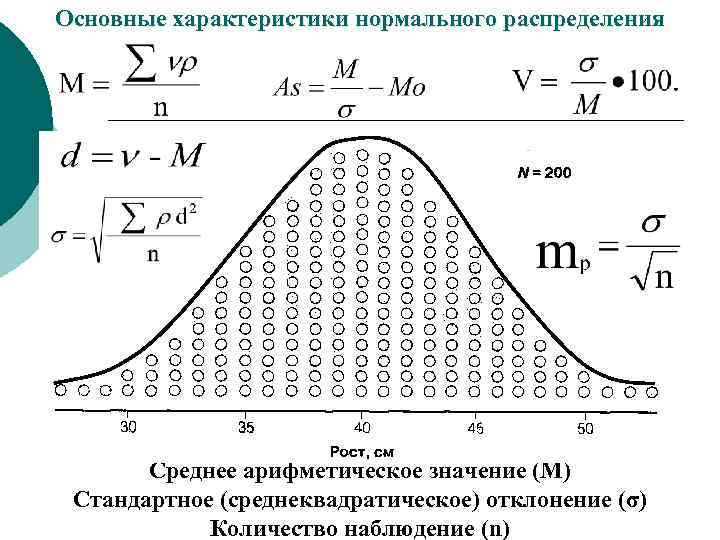
Основные характеристики нормального распределения Среднее арифметическое значение (М) Стандартное (среднеквадратическое) отклонение (σ) Количество наблюдение (n)
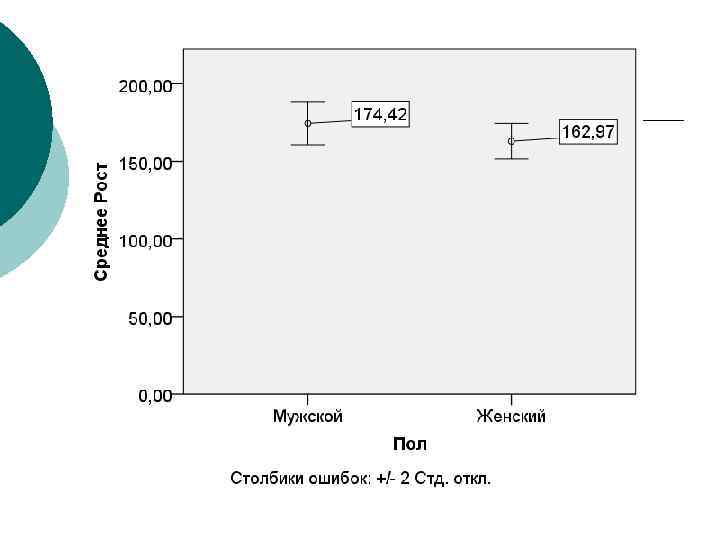
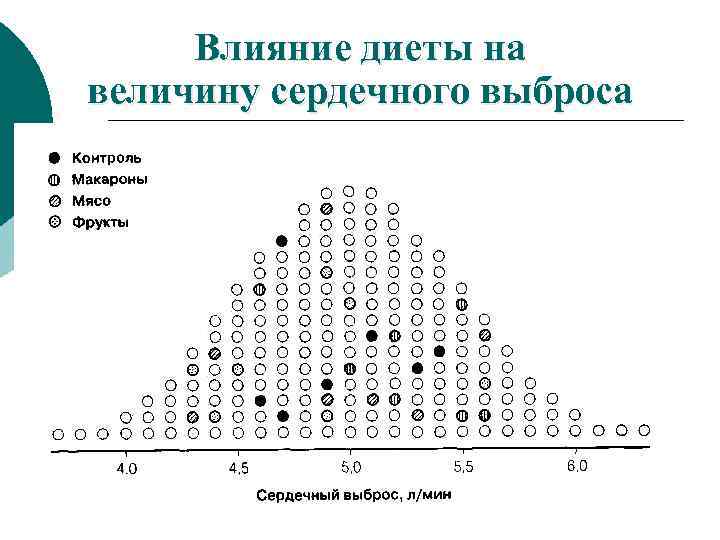
Влияние диеты на величину сердечного выброса

Общий принцип использования методов оценки статистической значимости межгрупповых различий 1. Формулировка нулевой гипотезы о случайности обнаруженных различий. 2. Определение вероятности получить наблюдаемые различия при условии справедливости нулевой гипотезы. 3. Подтверждение или отвержение нулевой гипотезы на основании сравнения вероятности, полученной в п. 2 с требуемым значением уровня значимости.

Формирование Выборок: Контроль Макароны Мясо Фрукты

Сравнение двух различных выборок

Две оценки дисперсии 1. Внутригрупповая дисперсия - среднее значение дисперсии, из дисперсий имеющихся выборок. 2. Межгрупповая дисперсия (дисперсия совокупности) - дисперсия результирующей выборки состоящей из средних арифметических первичных выборок


Где — выборочные оценки дисперсии в группах, питавшихся как обычно (контроль), макаронами, мясом и фруктами.

Две оценки дисперсии F = 1, при отсутствии различий в выборках.
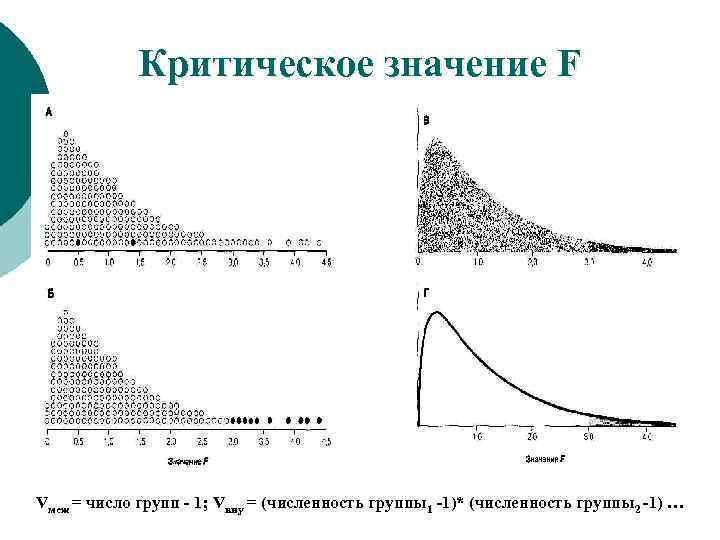
Критическое значение F Vмеж = число групп - 1; Vвну = (численность группы1 -1)* (численность группы2 -1) …
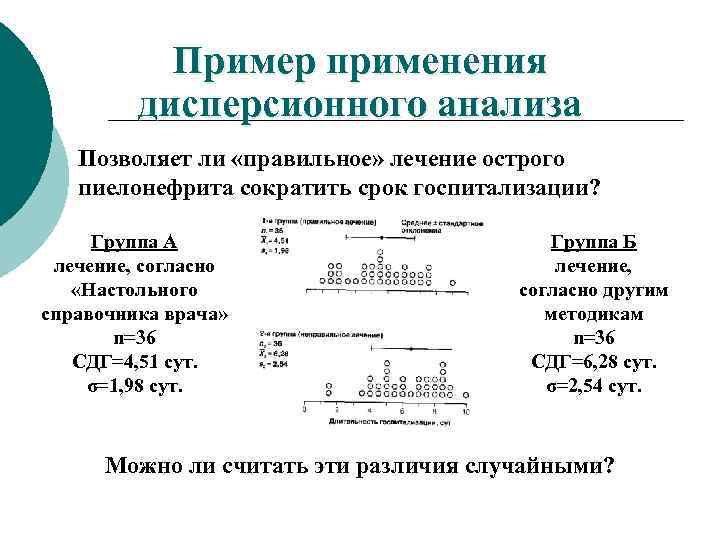
Пример применения дисперсионного анализа Позволяет ли «правильное» лечение острого пиелонефрита сократить срок госпитализации? Группа А лечение, согласно «Настольного справочника врача» n=36 СДГ=4, 51 сут. σ=1, 98 сут. Группа Б лечение, согласно другим методикам n=36 СДГ=6, 28 сут. σ=2, 54 сут. Можно ли считать эти различия случайными?

Проведение вычислений

Оценка коэффициента F Vмеж = 2 – 1= 1; Vвну = 36 -1 + 36 -1 = 70


Эффективность тестов Нулевая гипотеза Принята Отклонена Верна Правильно Ошибка I рода Неверна Ошибка II рода Правильно

Эффективность тестов Эффективность теста – это комплексная оценка точности статистического метода, включает два понятия: Ошибка I рода (альфа, α): вероятность найти различия там, где их нет (вероятность ошибочно отклонить нулевую гипотезу, вероятность ложноположительного результата) Ошибка II рода (бета, β): вероятность не найти различия там, где они есть (вероятность ошибочно принять нулевую гипотезу, вероятность ложноотрицательного результата)
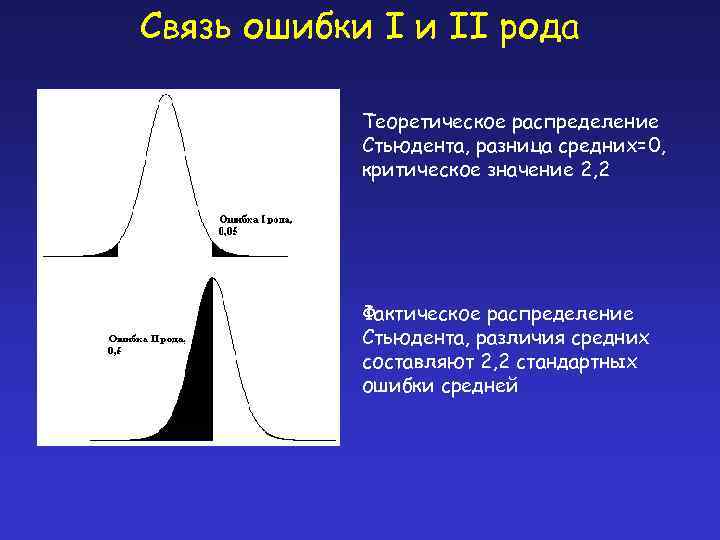
Связь ошибки I и II рода Теоретическое распределение Стьюдента, разница средних=0, критическое значение 2, 2 Фактическое распределение Стьюдента, различия средних составляют 2, 2 стандартных ошибки средней
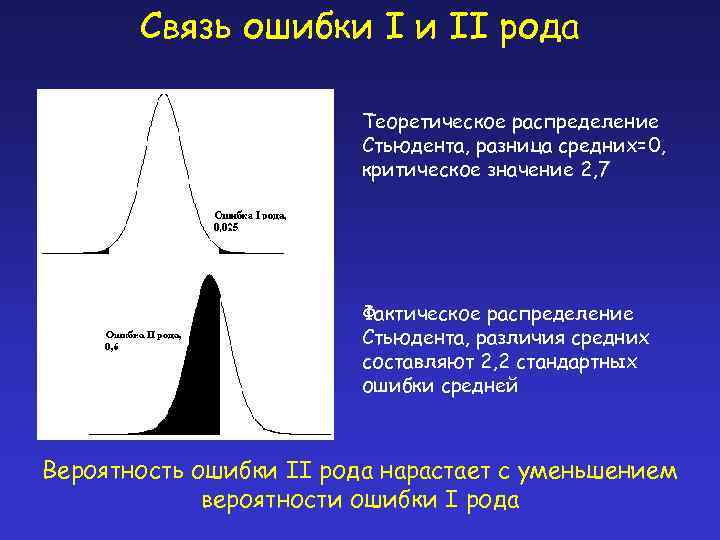
Связь ошибки I и II рода Теоретическое распределение Стьюдента, разница средних=0, критическое значение 2, 7 Фактическое распределение Стьюдента, различия средних составляют 2, 2 стандартных ошибки средней Вероятность ошибки II рода нарастает с уменьшением вероятности ошибки I рода
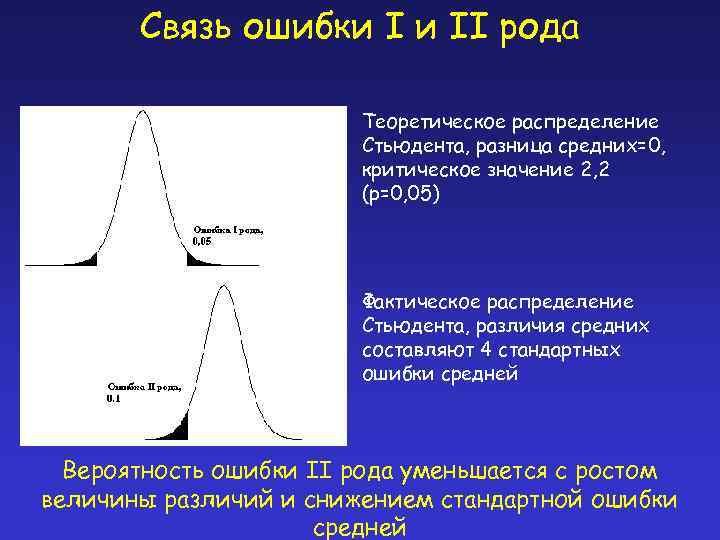
Связь ошибки I и II рода Теоретическое распределение Стьюдента, разница средних=0, критическое значение 2, 2 (p=0, 05) Фактическое распределение Стьюдента, различия средних составляют 4 стандартных ошибки средней Вероятность ошибки II рода уменьшается с ростом величины различий и снижением стандартной ошибки средней

Мощность теста = 1 – β Приемлемой считается β = 4α (для α = 0, 05; β = 0, 2; мощность = 80%) Повлиять на величину различий мы не можем, единственный вариант повысить мощность – снизить стандартную ошибку средней!

Как уменьшить стандартную ошибку? Стандартное отклонение – это тоже неизменяемое свойство. Следовательно, единственным путем для увеличения мощности и снижения числа ложноположительных результатов является увеличение объема выборки.

Доверительные интервалы для долей Доверительный интервал (confidence interval) для доли – это диапазон значений, в пределах которого с заданной вероятностью (обычно 95%) находится истинная популяционная доля. Для достаточно больших выборок распределение выборочных долей можно считать нормальным. Тогда: Доверительный интервал для доли: ДИ=p±tmp

Доверительные интервалы для долей, рассчитанные выше, являются лишь приблизительными. Точные доверительные интервалы рассчитываются, исходя из биномиального распределения. Вручную их можно определить по специальным номограммам, а на практике – в компьютерных статистических пакетах. Доверительные интервалы должны в обязательном порядке указываться для всех переменных при описании данных.

Доверительные интервалы для долей Пример: Исследователь указывает, что он исследовал 10 больных до и после лечения. Затем в таблице мы увидим, что до лечения боли в животе были у 70%, а после лечения – лишь у 20%. Данные выглядят очень убедительно - различия составляют 50%!. Теперь укажем доверительные интервалы: До лечения - 70% (42% - 98%), после лечения - 20% (0% - 44%). Доверительные интервалы даже перекрываются!. Применение доверительных интервалов показывает, какой диапазон значений может принимать показатель в популяции, а не в конкретной выборке.
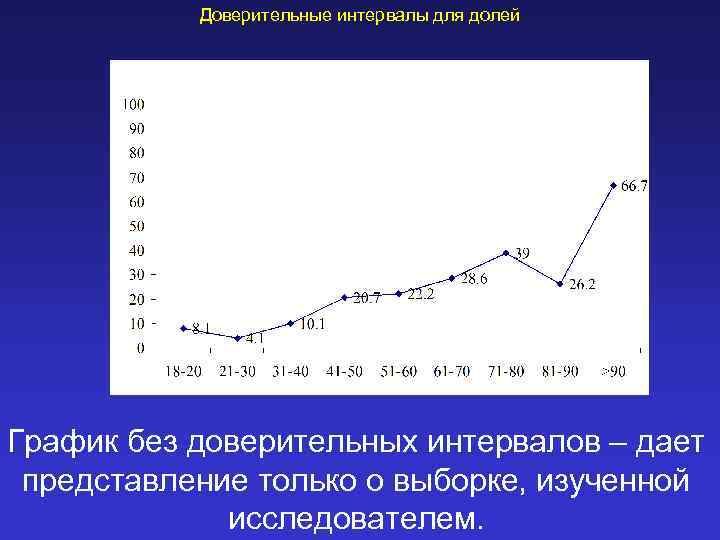
Доверительные интервалы для долей График без доверительных интервалов – дает представление только о выборке, изученной исследователем.
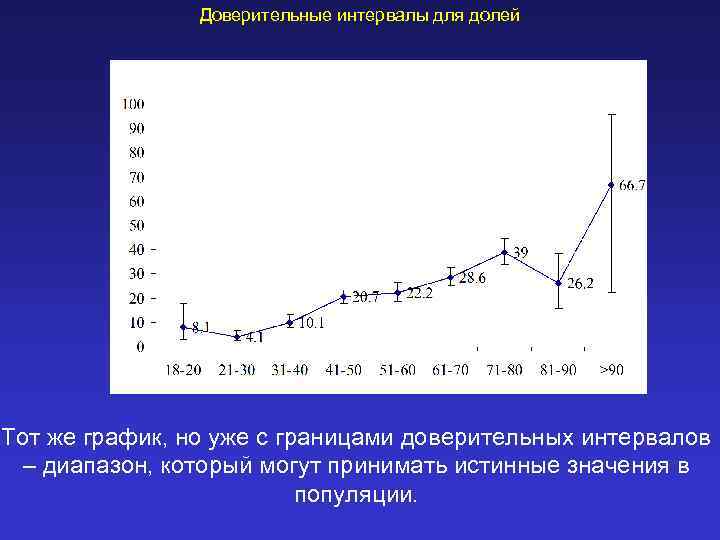
Доверительные интервалы для долей Тот же график, но уже с границами доверительных интервалов – диапазон, который могут принимать истинные значения в популяции.

Сравнительная статистика Для оценки достоверности относительных величин (Р), также как и для средних, необходимо рассчитывать их ошибку (mр). Расчет средней ошибки относительной величины производится по формуле: где Р - значение относительной величины, q - разница между базовым коэффициентом относительной величины и ее значением (100 — Р; 10 000 — Р и т. д. ), n - число наблюдений (при количестве наблюдений менее 30 в знаменатель берется выражение n — 1).

Благодарю за внимание

Подзаголовок презентации

Заголовок слайда р величина показателя изучаемого признака; q (100 p); t доверительный коэффициент, показывающий какова веро ятность того, что размеры показателя не будут выходить за гра ницы предельной ошибки (обычно берется t = 2, что обеспечива ет 95% вероятность безошибочного прогноза); — предельная ошибка показателя.

σ — показатель вариабельности признака (среднеквадратическое отклонение), который можно получить из предыдущих ис следований либо на основании пробных (пилотажных) исследо ваний. 47
4 Сравнительные статистики.pptx