SPSS Statistical Package for Social Sciences или в

SPSS (Statistical Package for Social Sciences или в новой интерпретации — Superior Performing Software Systems) — система (программный пакет) статистической обработки информации, которая предоставляет пользователю широкие возможности преобразования и анализа данных, а также наглядного представления полученных результатов

Файл исходной базы данных для проведения статистического анализа в SPSS формируется в редакторе данных (Data Editor). Редактор данных имеет две вкладки: «Представление переменные» (Variable View) и «Представление данные» (Datа View). Данные вкладки представляют собой таблицы, содержащие информацию о данных, собранных для проведения анализа.

Во вкладке редактора данных «Представление переменные» представлена таблица с данными, описывающими значения переменных. Каждый столбец отображает переменную (вопрос анкеты), каждая строка — отдельное наблюдение (объект сбора информации). В качестве объектов сбора информации могут выступать люди, предприятия, продукты, бренды и т. д.

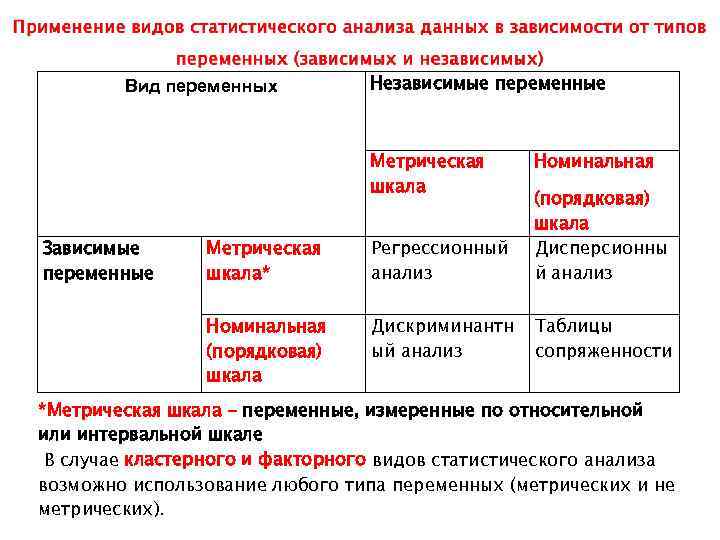Вид переменных Независимые переменные Метрическая шкала Номинальная Метрическая шкала* Регрессионный анализ Номинальная (порядковая) шкала Зависимые переменные (порядковая) шкала Дисперсионны й анализ Дискриминантн ый анализ Таблицы сопряженности *Метрическая шкала – переменные, измеренные по относительной или интервальной шкале В случае кластерного и факторного видов статистического анализа возможно использование любого типа переменных (метрических и не метрических).

Дисперсионный анализ изучает влияние категориальной переменной (фактора)- номинальной или порядковой на количественные переменные (интервальные или относительные)

Примеры задач, решаемых с помощью дисперсионного анализа: - Как уровень рекламы и уровень цен (высокий, средний, низкий) одновременно влияют на продажи товара данной торговой марки? - Связан ли выбор потребителей данной торговой марки с уровнем образования (ниже среднего, среднее, колледж, высшее) и возрастом? - Как осведомленность об универмаге (высокая, средняя, низкая) и представление о нем (позитивное, нейтральное, негативное) влияют на предпочтение потребителем этого магазина?

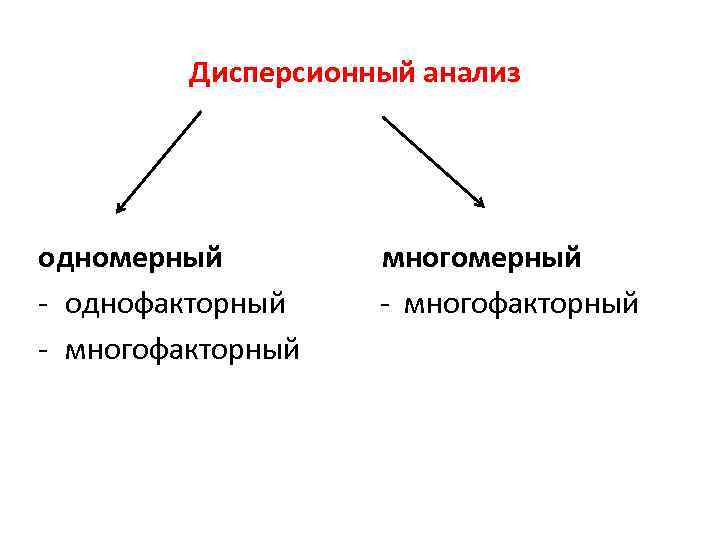Дисперсионный анализ одномерный многомерный - однофакторный - многофакторный

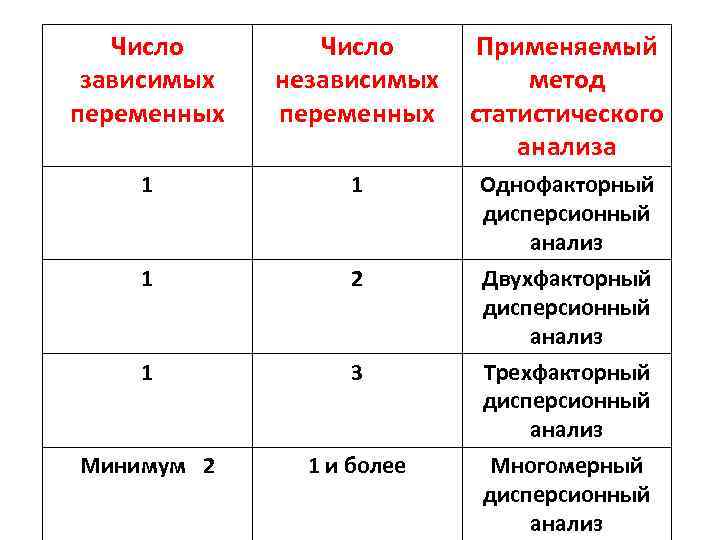Число зависимых переменных Число Применяемый независимых метод переменных статистического анализа 1 1 Однофакторный дисперсионный анализ Двухфакторный дисперсионный анализ 1 2 1 3 Трехфакторный дисперсионный анализ Минимум 2 1 и более Многомерный дисперсионный анализ

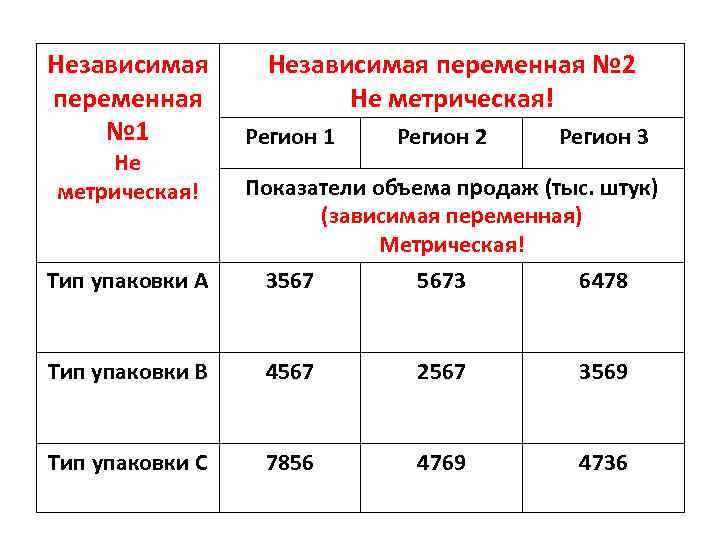Независимая переменная № 1 Не метрическая! Независимая переменная № 2 Не метрическая! Регион 1 Регион 2 Регион 3 Показатели объема продаж (тыс. штук) (зависимая переменная) Метрическая! Тип упаковки А 3567 5673 6478 Тип упаковки В 4567 2567 3569 Тип упаковки С 7856 4769 4736

Однофакторный дисперсионный анализ Устанавливает, значимо ли различаются средние значения нескольких независимых выборок. Нулевая гипотеза (H 0) утверждает, что k генеральных совокупностей имеют одно и то же среднее значение. То есть категориальный фактор не влияет на количественную переменную. Альтернативная гипотеза (H 1) утверждает, что средние значения не все равны между собой. По крайней мере они различаются у двух совокупностей.

Для проверки нулевой гипотезы обычно используют тест Ливина F-критерий Фишера и величину значимости (значимость полученного результата). Если величина значимости меньше величины 0, 05, то делается вывод о том, что гипотеза о равенстве средних значений отвергнута с вероятностью ошибки 0%, то есть различия в средних значениях для разных групп неслучайны!

Меню: Сравнение средних: Однофакторный дисперсионный анализ Перемещаем зависимую переменную в окно справа и категориальный фактор Диалоговое окно «Апостериорные множественные сравнения» : Шеффе, Т 2 Тамхейна Диалоговое окно «Параметры» : Статистики: описательные «Ок» и запуск процедуры дисперсионного анализа

- Исследуется покупательское поведение потребителей глазированных сырков. Респонденты разделяются на целевые группы в зависимости от их пола (q 3), возраста (q 4) и количества членов семьи (q 72). Одним из вопросов анкеты является: «Какое количество глазированных сырков в среднем Вы покупаете за одно посещение магазина? » (q 6) с вариантами ответа: 1 шт. , 2 шт. , 3 шт. , 4 шт. , 5 шт. , 6 -7 шт. , 8 -10 шт. и более 10 шт. - Требуется выяснить, различается ли кратность покупок глазированных сырков различными целевыми группами респондентов (половыми, возрастными и по количеству членов семьи).

- Прежде всего мы проведем однофакторный одномерный дисперсионный анализ и - установим, насколько значимо различается кратность покупок в различных возрастных - группах респондентов (1 — младше 18 лет; 2 — 19 -35 лет; 3 — 36 -60 лет; 4 — старше 60 - лет).

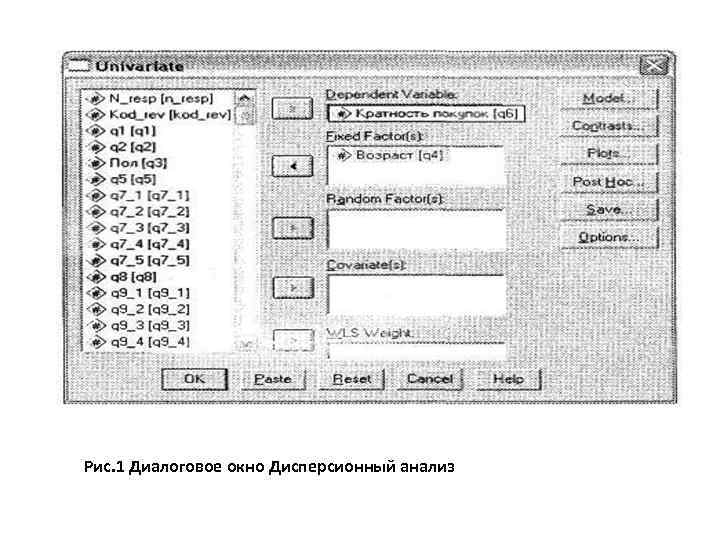Рис. 1 Диалоговое окно Дисперсионный анализ

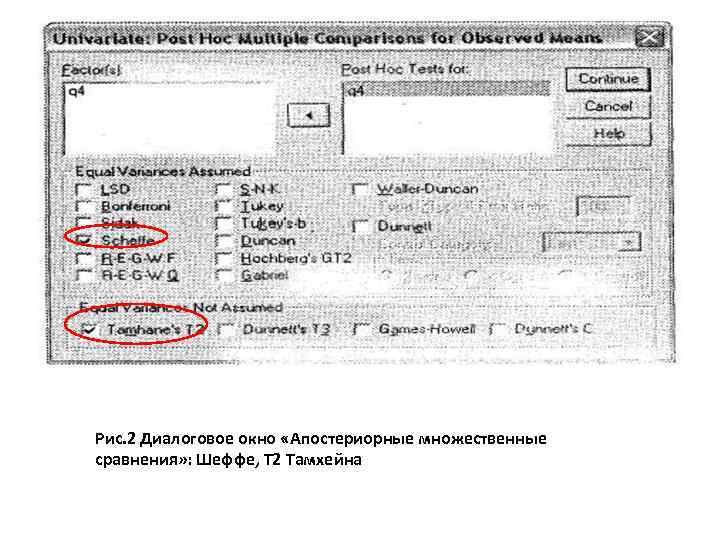Рис. 2 Диалоговое окно «Апостериорные множественные сравнения» : Шеффе, Т 2 Тамхейна

- Первой практически значимой таблицей является результат теста на равенство дисперсий зависимой и независимых переменных тест Ливина - В столбце Sig. данной таблицы содержится единственное интересующее нас значение — это статистическая значимость тестовой статистики F.

Рис. 3 Результаты Теста Ливина

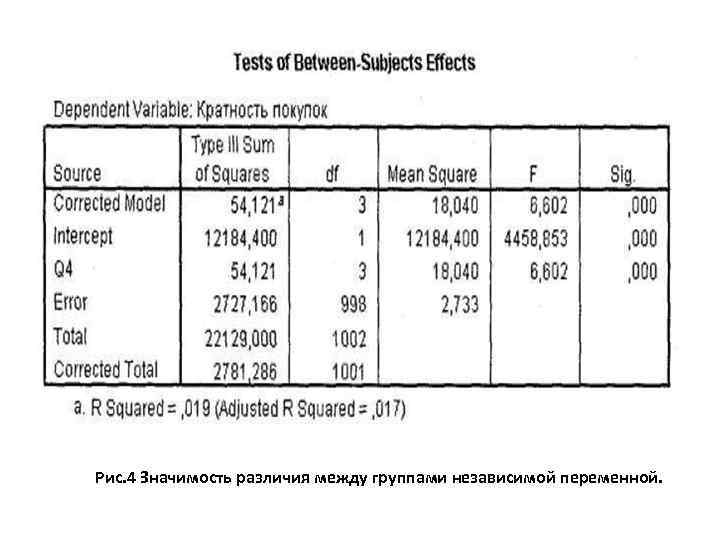Рис. 4 Значимость различия между группами независимой переменной.

- Первое, на что следует обратить внимание при анализе описываемой таблицы, — это величина R 2, отражающая долю совокупной дисперсии в зависимой переменной, описываемой статистической моделью. Другими словами, это та часть вариации зависимой переменной, которую можно объяснить на основании независимой переменной. Естественно, что чем меньше независимых переменных, тем меньше величина R 2, и наоборот.

- Второе - значимость различия между группами независимой переменной. Этот вывод следует из значения на пересечении строки, содержащей соответствующую независимую переменную, и столбца Sig.

- После того как мы установили наличие статистически значимого различия между - возрастными группами респондентов на основании кратности покупок сырков, необходимо определить, какие из четырех имеющихся возрастных групп отличаются от остальных и каким образом (в большую или в меньшую сторону).

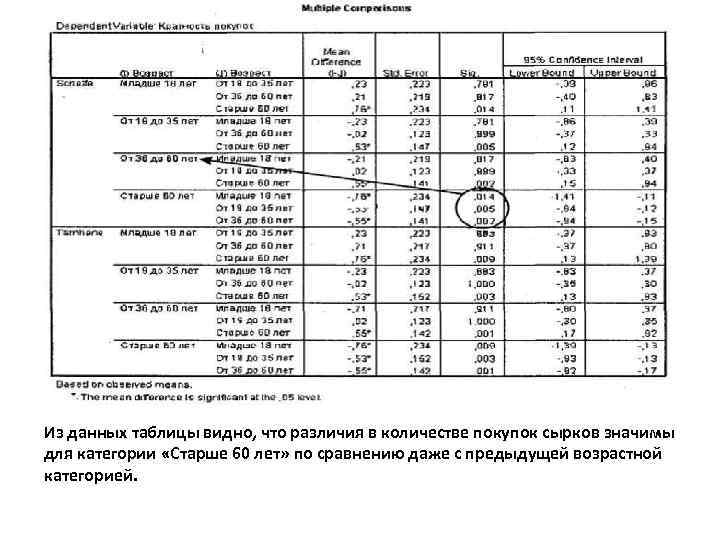Тема 1. Т-тесты и дисперсионный анализ Из данных таблицы видно, что различия в количестве покупок сырков значимы для категории «Старше 60 лет» по сравнению даже с предыдущей возрастной категорией.

Тема 1. Т-тесты и дисперсионный анализ - Так, в нашем случае мы можем заключить, что респонденты старше 60 лет покупают глазированные сырки в меньших объемах, чем респонденты младше 60 лет. В точности определить размер или величину различия можно, только если в качестве зависимой переменной выступает интервальная переменная. Так как у нас переменная q 6 Кратность покупок относится к порядковой шкале, мы не можем сделать точный вывод о величине различия.

- Рассмотрим теперь ситуацию, когда необходимо исследовать сразу две независимые переменные (и взаимодействия между ними), то есть выполнить двухфакторный одномерный дисперсионный анализ. - Исходные данные останутся такими же, как в предыдущем примере, однако теперь мы будем устанавливать различие в кратности покупок сырков возрастными и половыми группами (переменная q 3).

Меню «Обобщенная линейная модель» : ОЛМ одномерная Переносим зависимую переменную и независимые факторы в соответствующие окна справа Диалоговое меню «Апостериорные множественные сравнения для наблюденных средних» Переносим факторы в окно «Апостериорные критерии» , Шеффе, Т 2 Тамхейна Диалоговое окно «Параметры» факторы перенести в «Вывести средние для: » Вывести: Критерии однородности

Рис. 6 Результаты теста Ливина

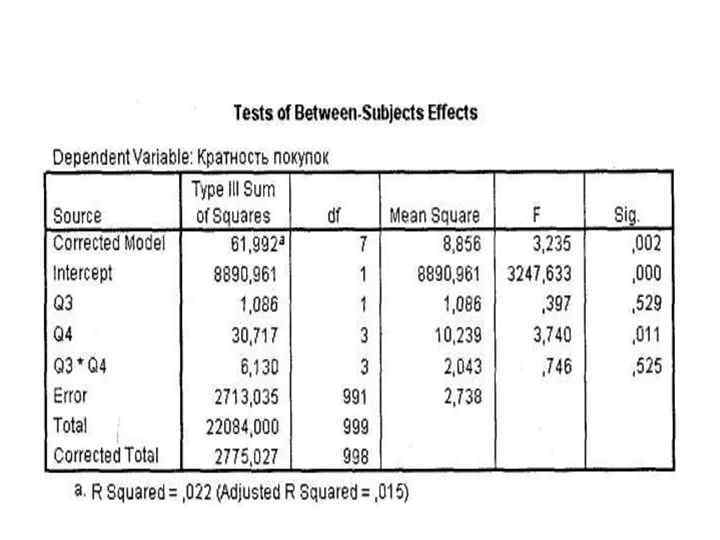
- Как видно, мужчины и женщины не имеют статистически значимых различий по кратности покупок глазированных сырков. То же относится и к взаимодействию q 3*q 4: оно не является статистически значимым. При этом, несмотря на неравенство дисперсий (порог значимости возрос до 0, 01), переменная q 4 (Возраст) сохранила свое значимое влияние на зависимую переменную (Sig. = 0, 011), то есть возрастные группы по-прежнему различаются по кратности покупок сырков. Необходимо также отметить, что с добавлением переменной q 3 доля совокупной дисперсии в зависимой переменной, объясняемая построенной моделью, несколько возросла (R 2 = 0, 022).

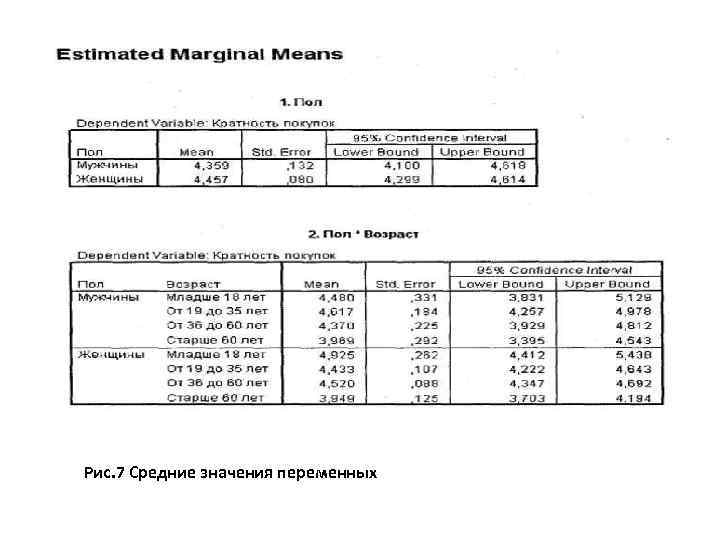Тема 1. Т-тесты и дисперсионный анализ Рис. 7 Средние значения переменных

- Так, если предположить, что влияние переменной Пол статистически значимо, то можно было бы заключить, что женщины покупают глазированные сырки в больших объемах по сравнению с мужчинами. То же можно сказать и относительно второй таблицы (Пол х Возраст).

ДИСКРИМИНАНТНЫЙ АНАЛИЗ

Определение Дискриминантный анализ – раздел многомерного статистического анализа, включающий в себя методы КЛАССИФИКАЦИИ многомерных наблюдений по принципу максимально СХОДСТВА при наличии ОБУЧАЮЩИХ признаков.

Ограничения использования Дискриминантный анализ используется в тех случаях, когда заранее известно число групп, на которые необходимо разбить набор объектов, а также имеется набор объектов, по которым уже известно, к каким группам они принадлежат. (пример: люди, купившие товар одной из конкурирующих марок)

Ограничения использования Дискриминантный анализ используется в случае, когда зависимая переменная - номинальная или порядковая (ее еще называют классифицирующей), а независимые переменные – количественные (допускаются порядковые)

Задачи, решаемые с помощью применения дискриминантного анализа: • Определение решающих правил, позволяющих по значению количественных признаков (независимых переменных) отнести каждый объект к одному из известных классов – составление классифицирующей функции; • Классификация неизвестных объектов при наличии данных по известным объектам, то есть прогнозирование, в какой группе будет относиться неизвестный объект по известным о нем характеристикам.

Примеры задач • Определить, на основании каких характеристик потребитель выбирает товар и предсказать выбор еще не определившихся потребителей (!ограничение: либо берем количественные характеристики, либо опрос по важности характеристик по шкале важности) • Определить, существует ли зависимость факта покупки ( «купил» /» не купил» ) в магазине от таких переменных как время посещения магазина, время пребывания в магазине, количество людей в магазине, время консультации с продавцом, …

Примеры задач • - обосновать выбор категории заведений общественного питания (кафе, бар, ресторан, кофейня, кондитерская) в зависимости от степени выраженности различных факторов (чувство голода посетителя, наличие компании, ассортимент заведения, количество людей в заведении, …); • - обосновать выбор марок спортивной одежды различными группами потребителей (профессионалы, любители, приверженцы активного отдыха, новички).

Пример • Определить, существует ли зависимость выбора йогурта от важности для потребителя таких характеристик как состав и вкус • Опрашивались потребители 2 марок йогурта: Активия и Даниссимо • Важность вкусовых характеристик и состава была оценена респондентами по 8 -балльной шкале, где 1 – совсем не важно, 8 – критически важно

Порядок действий 1. Определить группы данных (из постановки задачи или по результатам кластерного анализа) В рассматриваемом примере группы данных 2 – две марки йогурта !!! Количество групп не должно быть больше, чем количество независимых переменных Если мы рассматриваем всего 2 характеристики (вкус и польза), то можем проанализировать предпочтения потребителей только 2 марок. Если марок, которые необходимо включить в исследование, больше 2, то надо увеличивать количество рассматриваемых характеристик

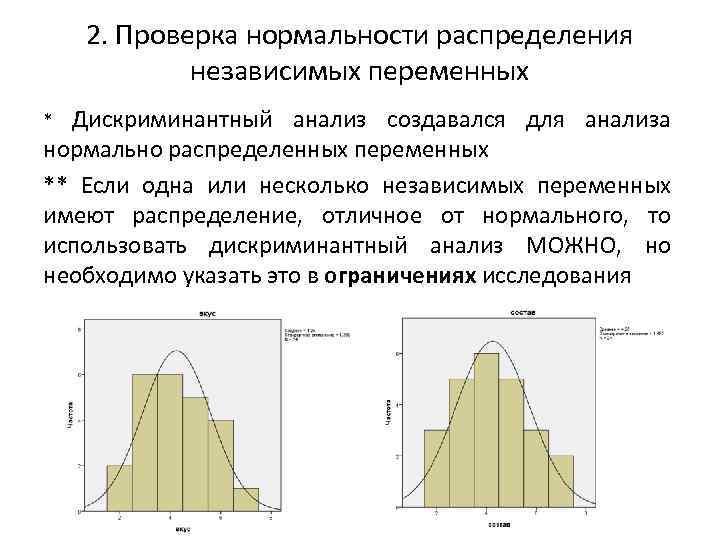2. Проверка нормальности распределения независимых переменных Дискриминантный анализ создавался для анализа нормально распределенных переменных ** Если одна или несколько независимых переменных имеют распределение, отличное от нормального, то использовать дискриминантный анализ МОЖНО, но необходимо указать это в ограничениях исследования *

3. Проверка значимости различий средних значений в полученных группах данных – проверить, если ли зависимость выбора йогурта от важности для респондента рассматриваемых характеристик • • Если значимость больше 0, 05* – подтверждается гипотеза H 0 – нет значимого различия в средних значениях полученных классов данных – нет разницы в важности характеристик для потребителей разных йогуртов – дальше можно не смотреть Если значимость меньше 0, 05* - отвергается гипотеза H 0 и принимается гипотеза H 1 – существуют значимые различия в средних значениях полученных классов данных – для потребителей разных марок йогуртов существуют различия в их оценке важности вкуса и состава – продолжаем анализ * 0, 05 – общепринятый уровень значимости проведении количественных исследований

4. Составление классифицирующей функции X 1 = 1, 729*вкус +1, 280*состав-6, 597 X 2 = 3, 614*вкус+0, 247*состав-10, 223 Подставляем значения из таблицы с данными в каждую из классифицирующих функций, где результат X получается больше – ту марку и выбирает потребитель

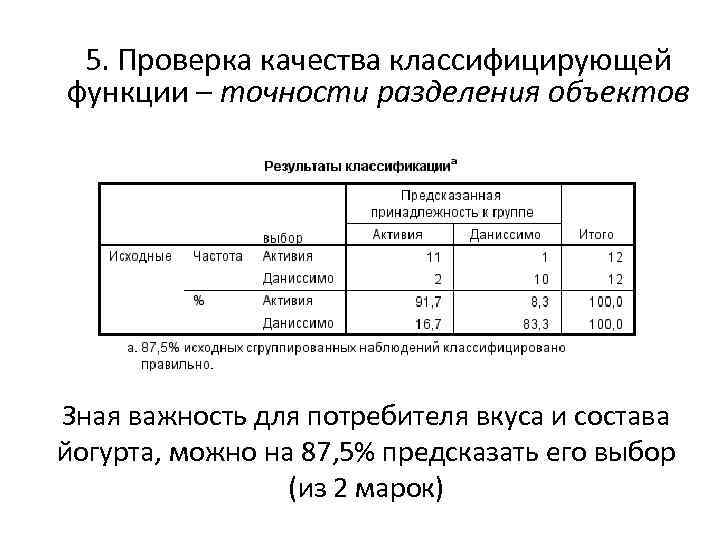5. Проверка качества классифицирующей функции – точности разделения объектов Зная важность для потребителя вкуса и состава йогурта, можно на 87, 5% предсказать его выбор (из 2 марок)

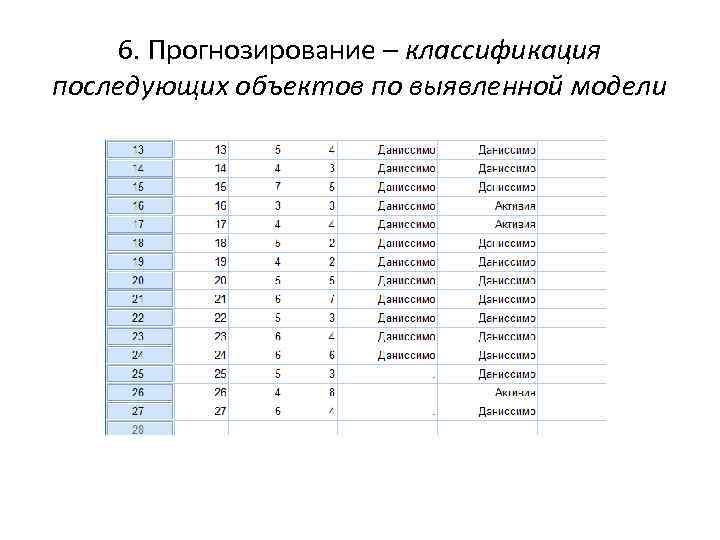6. Прогнозирование – классификация последующих объектов по выявленной модели

ОБОБЩИМ 1. Проверяем, чтоб независимые переменные были количественными (допускается порядковыми), а зависимая – номинальной или порядковой. 2. Проверяем, чтобы количество зависимых переменных было меньше либо равно количеству независимых 3. Проверяем нормальность распределения независимых переменных 4. Проводим процедуру дискриминантного анализа 5. Определяем, а существует ли вообще зависимость? (маркер: значимость<0, 05) 6. Находим классифицирующую функцию 7. Проверяем качество классифицирующей функции (маркер: % правильно классифицированных наблюдений) 8. Делаем прогноз

Задача Компания занимается продажей подержанных автомобилей и хочет составить модель для прогнозирования факта покупки авто в течение первого месяца после выставления на продажу в зависимости от следующих характеристик: • Цена авто (в у. е. ) • Техническое состояние (оценено по 10 балльной шкале, где 1 – очень плохое, 10 – отличное) • Возраст (в годах) • Пробег (в км)

Порядок действий в SPSS 1. Проверка нормальности распределения переменных (Анализ-Описательные статистики. Частоты-Диаграммы-Гистограммы) 2. Процедура дискриминантного анализа: Анализ – Классификация – Дискриминантный анализ - Выбор независимых и группирующей переменной (для группирующей переменной задать интервал значений) - В Статистиках отметить коэффициент Фишера, в Классифицировать - Итоговая таблица

Порядок действий в SPSS 3. Анализируем таблицы: Лямбда Уилкса, Коэффициенты классифицирующей функции, Результаты классификации 4. Делаем прогноз: вводим новые данные и повторяем процедуру дискриминантного анализа (дополнительно в меню Сохранить выбираем пункт Предсказанная принадлежность к группе)

Корреляционный анализ выявляет наличие, а также определяет направление и силу линейной связи между несколькими переменными, имеющими интервальный, порядковый или дихотомический тип шкалы.

Основные характеристики переменных Зависимые переменные Метод Количес Тип тво Корреляцио нный анализ Линейная регрессия Одна Независимые переменные Количеств Тип о Любое Интервальна я Порядковая Дихотомиче ская Интервальна Любое я Порядковая Интервальна я Порядковая Дихотомиче

Коэффициенты корреляции Коэффициент корреляции Распределение переменных Шкала Формула Корреляция Пирсона (корреляция моментов произведения) Нормальное Интервальная Количественная Ранговая корреляция Спирмена или Кендала Не является нормальным (хотя бы у одной переменной) Порядковая шкала Спирмена: (хотя бы у одной переменной) Кендала: (рекомендуется при наличии выбросов)

Коэффициенты корреляции Коэффициент корреляции варьируются от -1 до +1. -1 соответствует абсолютно разнонаправленной зависимости (с возрастанием одной переменной другая убывает); +1 соответствует абсолютно сонаправленной зависимости (то есть при возрастании одной переменной другая тоже возрастает); 0 показывает полное отсутствие всякой связи.

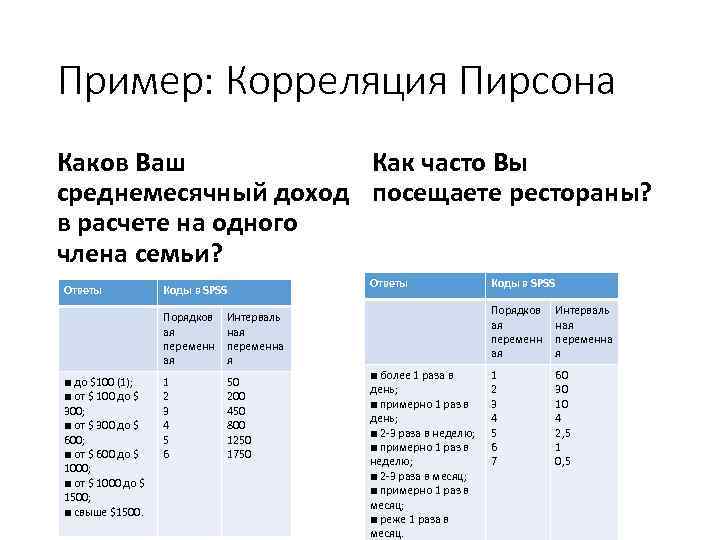Пример: Корреляция Пирсона Каков Ваш Как часто Вы среднемесячный доход посещаете рестораны? в расчете на одного члена семьи? Ответы Коды в SPSS Порядков ая переменн ая ■ до $100 (1); ■ от $ 100 до $ 300; ■ от $ 300 до $ 600; ■ от $ 600 до $ 1000; ■ от $ 1000 до $ 1500; ■ свыше $1500. 50 200 450 800 1250 1750 Порядков ая переменн ая Интерваль ная переменна я 1 2 3 4 5 6 Коды в SPSS ■ более 1 раза в день; ■ примерно 1 раз в день; ■ 2 -3 раза в неделю; ■ примерно 1 раз в неделю; ■ 2 -3 раза в месяц; ■ примерно 1 раз в месяц; ■ реже 1 раза в месяц. Интерваль ная переменна я 1 2 3 4 5 6 7 60 30 10 4 2, 5 1 0, 5

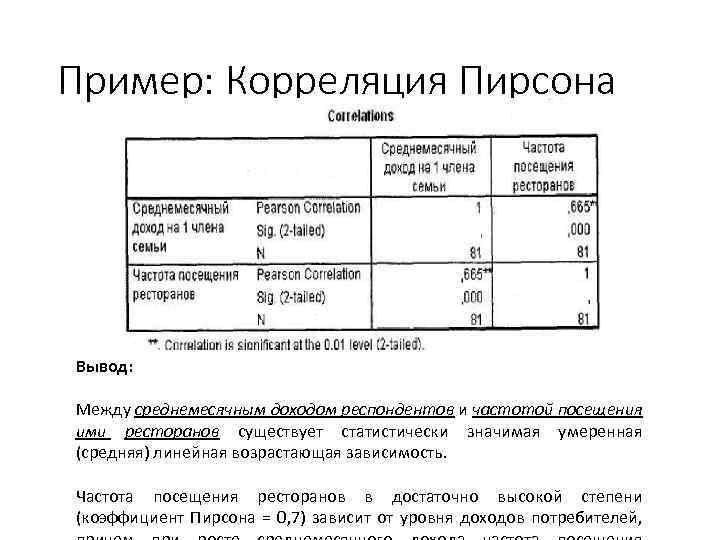Пример: Корреляция Пирсона Вывод: Между среднемесячным доходом респондентов и частотой посещения ими ресторанов существует статистически значимая умеренная (средняя) линейная возрастающая зависимость. Частота посещения ресторанов в достаточно высокой степени (коэффициент Пирсона = 0, 7) зависит от уровня доходов потребителей,

Пример: Корреляция Спирмена Какие факторы для Вас наиболее важны при выборе одежды? ■ Высокое качество одежды. ■ Доступные цены. ■ Широта ассортимента одежды. ■ Близость к дому или работе. ■ Высокое качество обслуживания. ■ Красивый интерьер магазина. Оцените, пожалуйста, следующие характеристики данного магазина одежды (вкотором происходит опрос) по пятибалльной шкале (от 1 — очень плохо до 5 — отлично) • ■ Высокое качество одежды. • ■ Доступные цены. • ■ Широта ассортимента одежды. • ■ Близость к дому или работе. • ■ Высокое качество обслуживания. • ■ Красивый интерьер магазина. • ■ Ваша общая оценка работы данного магазина.

Пример: Корреляция Спирмена

Пример: Корреляция Спирмена Вывод: Две рассматриваемые схемы выбора различаются несущественно. Данный вывод следует из сильной корреляции между переменными sc_l и sc_2 (коэффициент корреляции Спирмена = 0, 9), характеризующейся весьма высокой статистической значимостью (0, 005).

Регрессионный анализ • определяет степень детерминированности различий значений (вариаций) зависимой переменной у разных наблюдений независимой(ыми) переменной(ыми); • предсказывает значения зависимой переменной с помощью независимой(ых); • определяет вклад отдельных независимых переменных в вариацию зависимой.

Регрессионный анализ в маркетинговых исследованиях • Какие частные параметры продукта оказывают влияние на общее впечатление потребителей от данного продукта? Например, требуется установить, как влияет возраст и пол респондента на частоту покупок шоколадок (построение уравнения с целью прогноза). • Какие частные характеристики продукта в большей степени влияют на цену продукта? Например, требуется установить, что влияет в большей степени на цену: материал продукта или цвет продукта (установление соотношения между различными частными параметрами по силе и направлению влияния на общее впечатление). • Как ведет себя одна переменная в зависимости от изменения другой? Например, необходимо построить график зависимости осведомленности о шоколадках и частоты покупки. Как изменится частота покупок при увеличении осведомленности покупателя на 10%. (графическое прогнозирование – только для двух переменных)

Основные характеристики переменных Зависимые переменные Метод Количес Тип тво Корреляцио нный анализ Линейная регрессия Одна Независимые переменные Количеств Тип о Любое Интервальна я Порядковая Дихотомиче ская Интервальна Любое я Порядковая Интервальна я Порядковая Дихотомиче

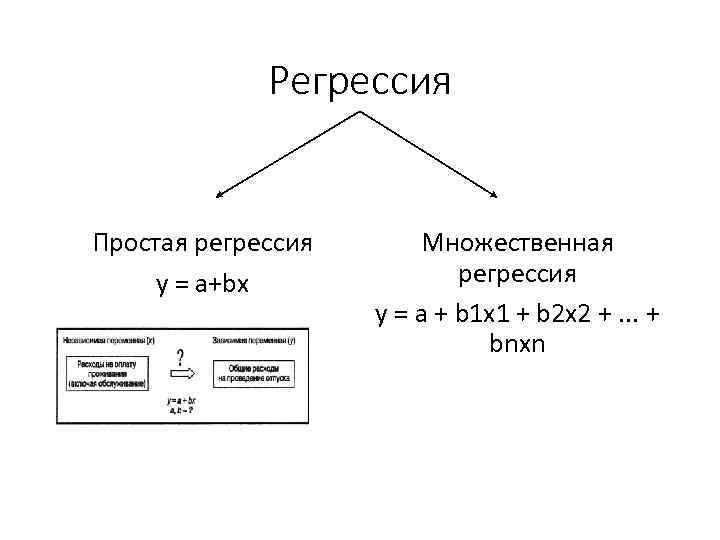Регрессия Простая регрессия y = a+bx Множественная регрессия у = а + b 1 х1 + b 2 х2 +. . . + bnхn

Пример: множественная линейная регрессия Респонденты трёх классов: • Первый класс • Бизнес-класс • Эконом-класс Необходимо: 1) Выявить наиболее значимые для респондентов параметры обслуживания на борту. 2) Установить, какое влияние оказывают оценки частных параметров обслуживания на борту на общее впечатление авиапассажиров от полета. Оцените по пятибалльной шкале следующие характеристики сервиса на борту авиакомпании X (1 – очень плохо, 5 – отлично): • комфортабельность салона, • работа бортпроводников, • питание во время полета, • цена билетов, • спиртные напитки, • дорожные наборы, • аудиопрограммы, • видеопрограммы, • пресса, • общая оценка.

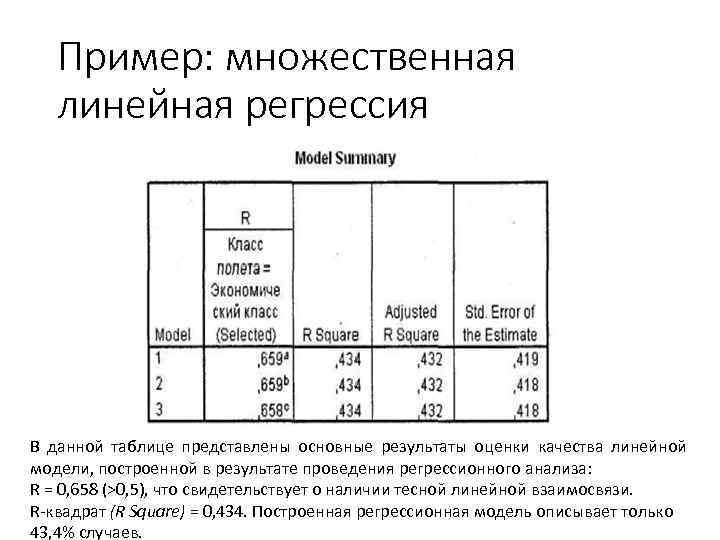Пример: множественная линейная регрессия В данной таблице представлены основные результаты оценки качества линейной модели, построенной в результате проведения регрессионного анализа: R = 0, 658 (>0, 5), что свидетельствует о наличии тесной линейной взаимосвязи. R-квадрат (R Square) = 0, 434. Построенная регрессионная модель описывает только 43, 4% случаев.

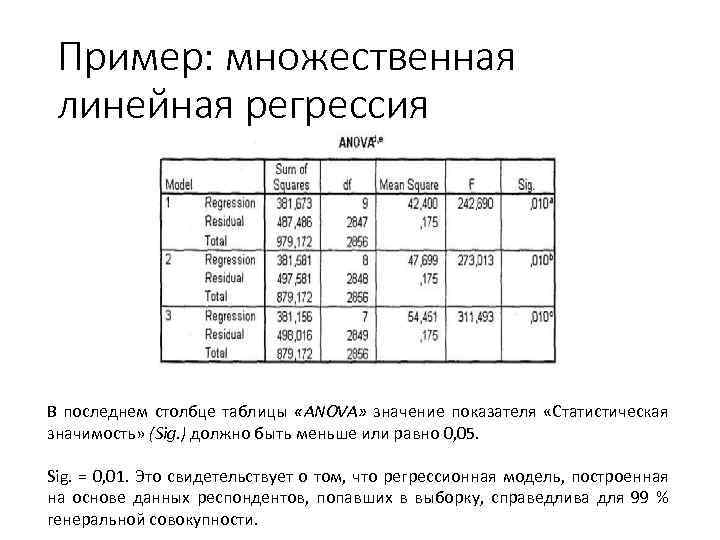Пример: множественная линейная регрессия В последнем столбце таблицы «ANOVA» значение показателя «Статистическая значимость» (Sig. ) должно быть меньше или равно 0, 05. Sig. = 0, 01. Это свидетельствует о том, что регрессионная модель, построенная на основе данных респондентов, попавших в выборку, справедлива для 99 % генеральной совокупности.

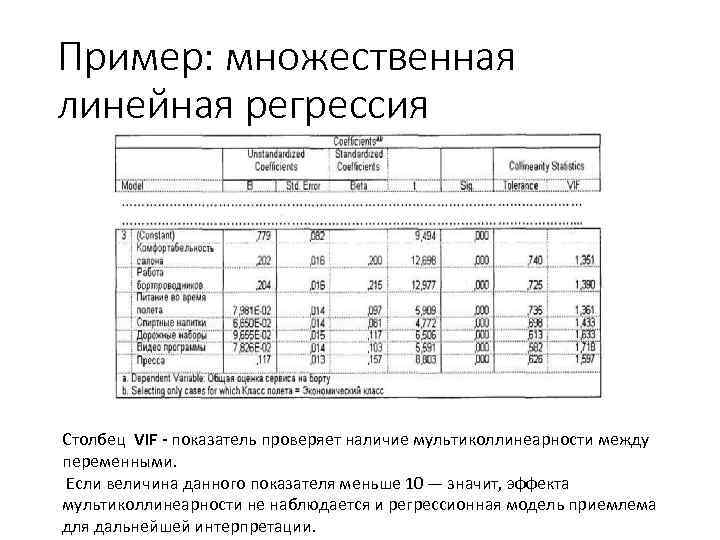Пример: множественная линейная регрессия Столбец VIF - показатель проверяет наличие мультиколлинеарности между переменными. Если величина данного показателя меньше 10 — значит, эффекта мультиколлинеарности не наблюдается и регрессионная модель приемлема для дальнейшей интерпретации.

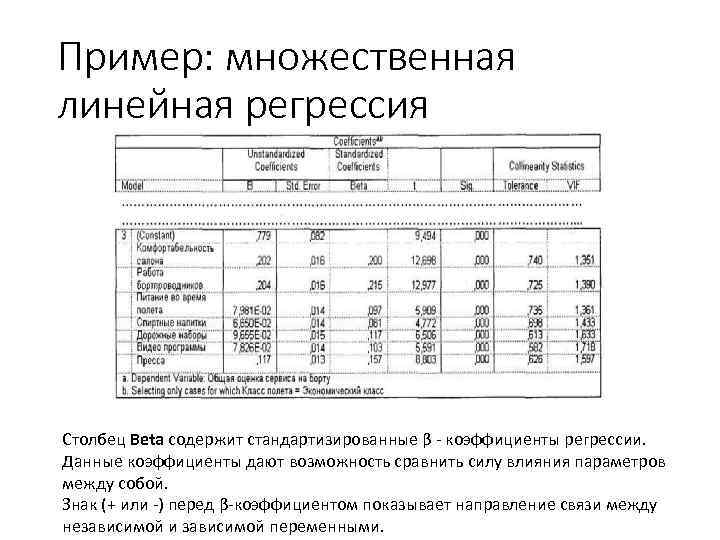Пример: множественная линейная регрессия Столбец Beta содержит стандартизированные β - коэффициенты регрессии. Данные коэффициенты дают возможность сравнить силу влияния параметров между собой. Знак (+ или -) перед β-коэффициентом показывает направление связи между независимой и зависимой переменными.

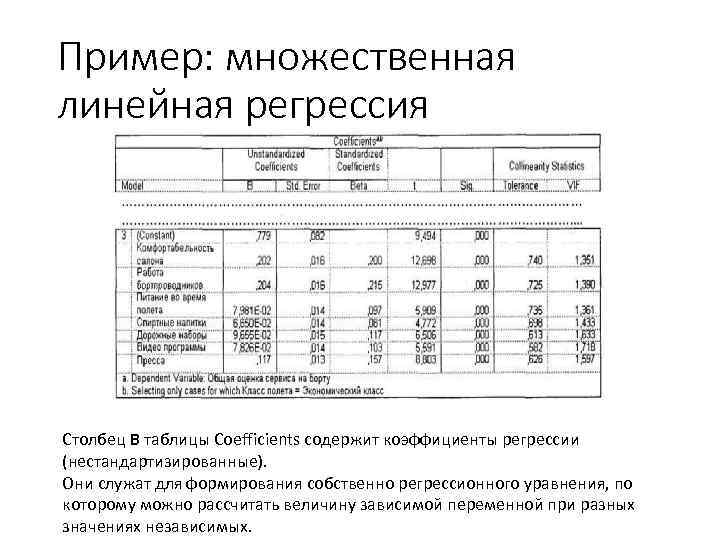Пример: множественная линейная регрессия Столбец В таблицы Coefficients содержит коэффициенты регрессии (нестандартизированные). Они служат для формирования собственно регрессионного уравнения, по которому можно рассчитать величину зависимой переменной при разных значениях независимых.

Пример: множественная линейная регрессия СБ = 0, 78 + 0, 20 К + 0. 20 Б + 0, 08 ПП + 0. 07 С + 0 Д 0 Н + 0, 08 В + 0 Д 2 П, где ■ СБ — общая оценка сервиса на борту; ■ К — комфортабельность салона; ■ Б — работа бортпроводников; ■ ПП — питание во время полета; ■ С — спиртные напитки; ■ Н — дорожные наборы; ■ В — видеопрограмма; ■ П — пресса.

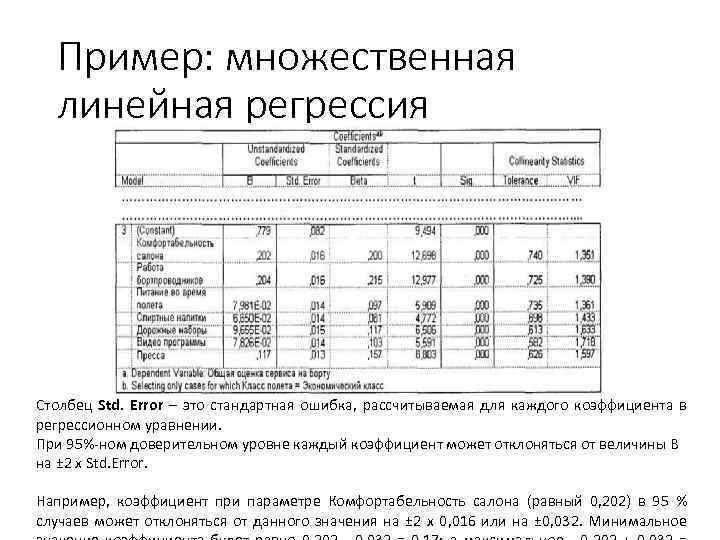Пример: множественная линейная регрессия Столбец Std. Error – это стандартная ошибка, рассчитываемая для каждого коэффициента в регрессионном уравнении. При 95%-ном доверительном уровне каждый коэффициент может отклоняться от величины В на ± 2 х Std. Error. Например, коэффициент при параметре Комфортабельность салона (равный 0, 202) в 95 % случаев может отклоняться от данного значения на ± 2 х 0, 016 или на ± 0, 032. Минимальное

Факторный анализ позволяет разделить массив переменных на малое число групп (факторов). Классификация переменных по различным факторам (группам) производится на основе коэффициента корреляции между исследуемыми переменными. В один фактор объединяются переменные, которые имеют высокий коэффициент корреляции друг с другом и не коррелируют или имеют низкий коэффициент корреляции с другими переменными, входящими в состав других факторов.

Факторный анализ в маркетинговых исследованиях Сегментирование рынка Факторный анализ применяется для выявления агрегатных переменных, являющихся основанием для сегментирования потребителей. Например, потребители плавленых сыров могут характеризоваться различной степенью значимости, которую они видят в исследуемых характеристиках данного продукта (респондентов просят оценить по пятибалльной шкале важность нескольких характеристик плавленых сыров: срок хранения, калорийность, процент жирности и т. д. ). Здесь факторный анализ позволит выявить целевые сегменты потребителей на основании значимости для них различных групп факторов: ■ покупатели, ориентирующиеся при выборе плавленого сыра преимущественно на ценовые факторы (стоимость, скидки); ■ покупатели, ориентирующиеся на качество исследуемого продукта (срок хранения, состав ингредиентов, вкус); ■ покупатели, выбирающие сыр в основном по внешнему виду (дизайн упаковки).

Факторный анализ в маркетинговых исследованиях Изучение продукта и бенчмаркинг продукта В данном случае факторный анализ помогает выявить агрегатные параметры продукта, влияющие на выбор потребителя. Например, различные марки шоколадных конфет могут быть оценены по следующим макрокатегориям: - качество (ингредиенты, вкус), - полезность для здоровья (наличие сахара, калорийность), - цена.

Факторный анализ в маркетинговых исследованиях Рекламные и медиа-исследования Факторный анализ может использоваться для выявления скрытых мотивов поведения потребителей при восприятии рекламы. Ценообразование Факторный анализ используется для выявления особенностей поведения потребителей, чувствительных к цене. Например, данная категория респондентов может характеризоваться повышенным вниманием к ценовым факторам при выборе продукта, низкими доходами, большой численностью семьи и т. д.

Основные характеристики переменных Зависимые переменные Метод Независимые переменные Количес Тип тво Количеств Тип о Факторный Нет анализ - Любое Любой

Пример: факторный анализ ql. Авиакомпания X обладает репутацией компании, превосходно обслуживающей пассажиров. q 2. Авиакомпания X может конкурировать с лучшими авиакомпаниями мира. ql 3. Мне нравится, как в настоящее время авиакомпания X представлена визуально широкой общественности (в плане цветовой гаммы и фирменного стиля). ql 4. Авиакомпания X — лицо России. q 3. Я верю, что у авиакомпании X есть перспективное будущее в мировой авиации. ql 5. Мы выглядим «вчерашним днем» по сравнению с другими авиакомпаниями. q 4. Я знаю, какой будет стратегия развития авиакомпании X в будущем. ql 6. Обслуживание авиакомпании Х является последовательным и узнаваемым во всем мире. q 5. Я горжусь тем, что работаю в авиакомпании X. ql 7. Я бы не хотел, чтобы авиакомпания X менялась. q 6. Внутри авиакомпании X хорошее взаимодействие между подразделениями. ql 8. Авиакомпании X необходимо меняться для того, чтобы использовать в полной мере имеющийся потенциал. q 7. Каждый сотрудник авиакомпании прикладывает все усилия для того, чтобы обеспечить ее успех. ql 9. Я думаю, что авиакомпании X необходимо представить себя в визуальном плане более современно. q 8. Сейчас авиакомпания X быстро улучшается. q 20. Изменения в авиакомпании X будут позитивным моментом. q 9. Нам предстоит долгий путь, прежде чем мы сможем претендовать на то, чтобы называться авиакомпанией мирового класса. q 21. Авиакомпания X — эффективная авиакомпания. ql. O. Авиакомпания X действительно заботится о пассажирах. q 22. Я бы хотел, чтобы имидж авиакомпании X улучшился с точки зрения иностранных пассажиров. qll. Среди сотрудников авиакомпании имеет место высокая степень удовлетворенности работой. q 23. Авиакомпания X — лучше, чем многие о ней думают. q 24. Важно, чтобы люди во всем мире знали, что мы — Выявить схожие (то есть тесно российская авиакомпания. между собой) коррелирующие утверждения и разделить их на несколько однородных групп, описывающих различные аспекты (макропараметры) конкурентной позиции авиакомпании X на рынке. Другими словами, выделить группы схожих по значению параметров авиакомпании, характеризующих ее ql 2. Я верю, что менеджеры высшего звена прикладывают все усилия для достижения успеха авиакомпании.

Пример: факторный анализ Результаты теста КМО позволяют сделать вывод относительно общей пригодности имеющихся данных для факторного анализа, то есть насколько хорошо построенная факторная модель описывает структуру ответов респондентов на анализируемые вопросы. Результаты данного теста варьируются в интервале от 0 (факторная модель абсолютно неприменима) до 1 (факторная модель идеально описывает структуру данных). Факторный анализ следует считать пригодным, если КМО находится в пределах от 0, 5 до 1. В рассматриваемом примере значение этого теста 0, 904 (табл. ), что свидетельствует о приемлемости построенной факторной модели. Статистикой, определяющей пригодность факторного анализа по тесту Barlett, является значимость (строка Sig. ). При приемлемом уровне значимости (ниже 0, 05) факторный анализ считается пригодным для анализа исследуемой выборочной совокупности. Из данных табл. видно, что значимость теста «Bartlett» (Sig. ) составляет 0, 000. Это означает, что исходная гипотеза может быть отклонена с

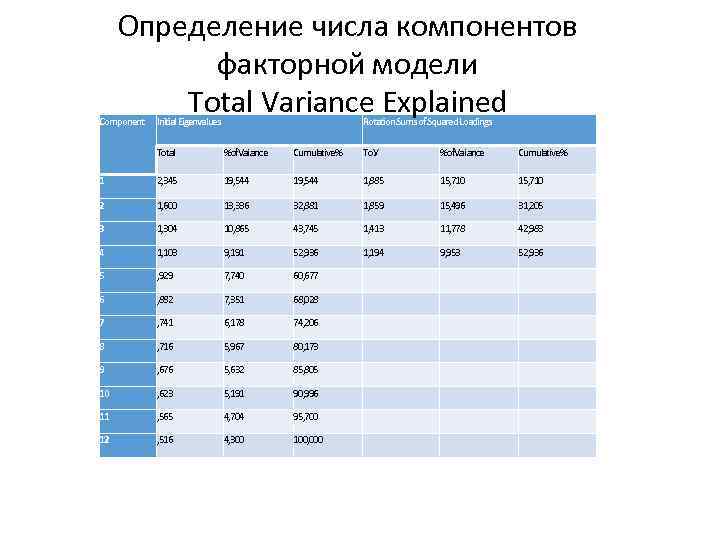Определение числа компонентов факторной модели Total Variance Explained Component Initial Eigenvalues Rotation Sums of Squared Loadings Total %of. Vai ance Cumulative % То. У %of. Vai ance Cumulative % 1 2, 345 19, 544 1, 885 15, 710 2 1, 600 13, 336 32, 881 1, 859 15, 496 31, 205 3 1, 304 10, 865 43, 745 1, 413 11, 778 42, 983 4 1, 103 9, 191 52, 936 1, 194 9, 953 52, 936 5 , 929 7, 740 60, 677 6 , 882 7, 351 68, 028 7 , 741 6, 178 74, 206 8 , 716 5, 967 80, 173 9 , 676 5, 632 85, 805 10 , 623 5, 191 90, 996 11 , 565 4, 704 95, 700 12 , 516 4, 300 100, 000

Определение числа компонентов факторной модели Total Variance Explained Число групп (компонентов) факторной модели определяется при помощи расчета «характеристических чисел» (Eigenvalues). Эти показатели характеризуют полноту отображения исходной информации в построенной факторной модели. В первом столбце табл. 5. 4 (Component) указывается число компонентов различных вариантов факторной модели. В четвертом столбце этой таблицы (Cumulative, %) показан процент информации, сохраненной в процессе группировки исходного массива переменных с помощью факторной модели. Например, если число факторов в факторной модели равно числу переменных исходного массива (в нашем примере 12), т. е. группировка переменных не производится, исходная информация будет сохранена на 100%. Во втором столбце таблицы (Total) указываются значения «характеристических чисел» (Eigenvalues). В рассматриваемом примере было задано условие: значение «характеристических чисел» должно быть больше единицы (Eigenvalues over 1) (см. рис. 5. 7). Максимальное значение компонентов фа^орной модели, в которой данный показатель превышает единицу, составляет 4. Это означает, что оптимальное число групп (факторов) в факторной модели составляет 4. Как видно из данных, представленных в табл. 5. 4, факторная модель, состоящая из 4 -х факторов, сохраняет лишь 52, 936% исходной информации. Как отмечалось ранее, при группировке исходного массива переменных потеря информации неизбежна. При построении факторной модели следует стремиться к минимизации потерь информации. Сохранение информации всего лишь на 52, 936% является не очень хорошим показателем. Однако, принимая во внимание, что в ходе факторного анализа число переменных сократится в 3 раза (с 12 до 4), а потеря информации составит менее 48%, применение построенной факторной модели следует считать целесообразным.

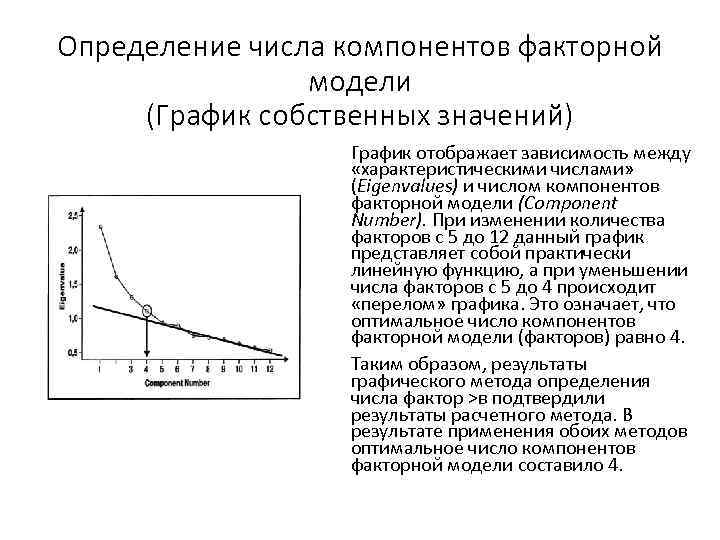Определение числа компонентов факторной модели (График собственных значений) График отображает зависимость между «характеристическими числами» (Eigenvalues) и числом компонентов факторной модели (Component Number). При изменении количества факторов с 5 до 12 данный график представляет собой практически линейную функцию, а при уменьшении числа факторов с 5 до 4 происходит «перелом» графика. Это означает, что оптимальное число компонентов факторной модели (факторов) равно 4. Таким образом, результаты графического метода определения числа фактор >в подтвердили результаты расчетного метода. В результате применения обоих методов оптимальное число компонентов факторной модели составило 4.

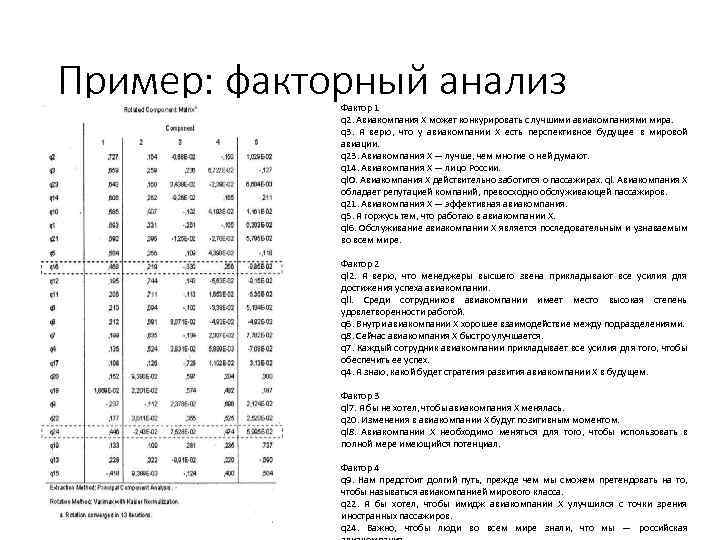Пример: факторный анализ Фактор 1 q 2. Авиакомпания X может конкурировать с лучшими авиакомпаниями мира. q 3. Я верю, что у авиакомпании X есть перспективное будущее в мировой авиации. q 23. Авиакомпания X — лучше, чем многие о ней думают. q 14. Авиакомпания X — лицо России. ql. O. Авиакомпания Х действительно заботится о пассажирах. ql. Авиакомпания X обладает репутацией компаний, превосходно обслуживающей пассажиров. q 21. Авиакомпания X — эффективная авиакомпания. q 5. Я горжусь тем, что работаю в авиакомпании X. ql 6. Обслуживание авиакомпании X является последовательным и узнаваемым во всем мире. Фактор 2 ql 2. Я верю, что менеджеры высшего звена прикладывают все усилия для достижения успеха авиакомпании. qll. Среди сотрудников авиакомпании имеет место высокая степень удовлетворенности работой. q 6. Внутри авиакомпании X хорошее взаимодействие между подразделениями. q 8. Сейчас авиакомпания X быстро улучшается. q 7. Каждый сотрудник авиакомпании прикладывает все усилия для того, чтобы обеспечить ее успех. q 4. Я знаю, какой будет стратегия развития авиакомпании X в будущем. Фактор 3 ql 7. Я бы не хотел, чтобы авиакомпания X менялась. q 20. Изменения в авиакомпании X будут позитивным моментом. ql 8. Авиакомпании X необходимо меняться для того, чтобы использовать в полной мере имеющийся потенциал. Фактор 4 q 9. Нам предстоит долгий путь, прежде чем мы сможем претендовать на то, чтобы называться авиакомпанией мирового класса. q 22. Я бы хотел, чтобы имидж авиакомпании X улучшился с точки зрения иностранных пассажиров. q 24. Важно, чтобы люди во всем мире знали, что мы — российская

Пример: факторный анализ ■ Фактор 1 характеризует общее положение авиакомпании X в глазах ее клиентов. ■ Фактор 2 характеризует внутреннее состояние авиакомпании X с точки зрения ее сотрудников. ■ Фактор 3 характеризует изменения, происходящие в авиакомпании X. ■ Фактор 4 характеризует имидж авиакомпании X. ■ Фактор 5 характеризует визуальный образ авиакомпании X.

Алгоритм • Анализ/Снижение размерности/Факторный анализ Перенести все переменные в окно с переменными • Описательные: Начальное решение, Корреляционная матрица (Коэффициенты, КМО и критерий сферичности Бартлетта) • Извлечение: Метод - Главные компоненты • Вращение: Метод – Варимакс • Значение факторов: Сохранить как переменные (Метод - Регрессия), Вывести матрицу коэффициентов значений факторов. • Параметры: Формат выводы коэффициентов (Отсортировать по величине, Не выводить коэффициенты с низким значением)

Алгоритм • Преобразование: Ранжировать наблюдения Типы рангов (Дробный ранг, N разбиение: 5)

Пример: факторный анализ Необходимо: Разделить респондентов на группы, путем снижения размерности.

Пример: факторный анализ

Иерархический кластерный анализ Классификационный метод анализа данных Цель – выделения однородных групп (кластеров) из исследуемой совокупности объектов (потребителей, продуктов, брендов и т. д. ). Эти кластеры должны быть однородными внутри и разнородными между собой!

Иерархический кластерный анализ используется для классификации набора объектов, когда заранее не известно число групп, на которые нужно этот набор разбить. Группы, на которые разбита выборка, называются кластерами. Число групп заранее не задается.

Примеры задач, решаемых с помощью кластерного анализа: - определение групп потребителей – сегментация (выделение существующих/ потенциальных); - когда на рынке присутствует большой выбор товаров одного назначения под разными торговыми марками. Необходимо разбить товары на группы схожих товаров; - определение потенциальных групп потребителей. Результаты классификации используются, чтобы в дальнейшем для разных групп определить оптимальные цены на услуги, оптимальные тарифы.

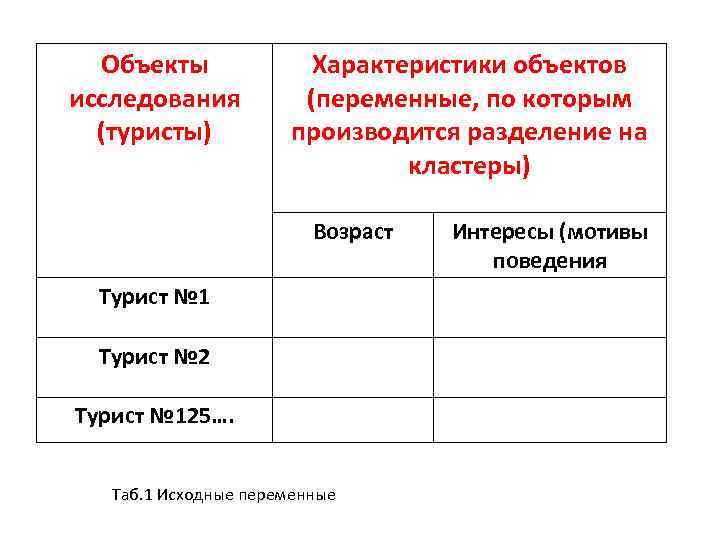Объекты исследования (туристы) Характеристики объектов (переменные, по которым производится разделение на кластеры) Возраст Турист № 1 Турист № 2 Турист № 125…. Таб. 1 Исходные переменные Интересы (мотивы поведения

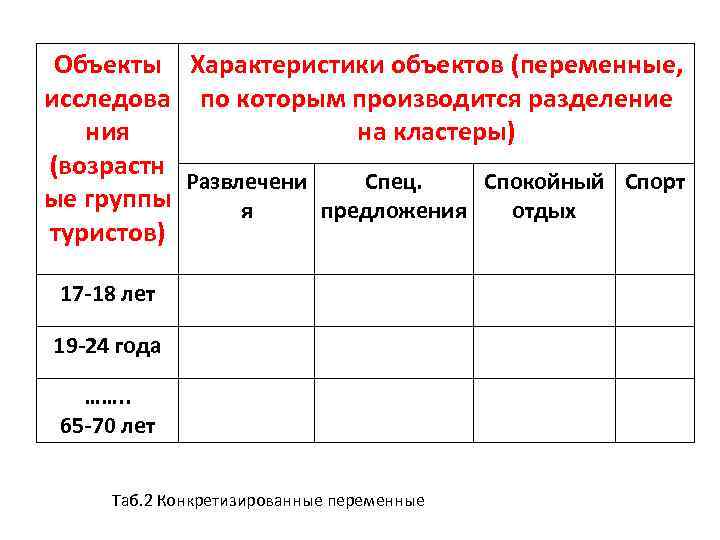Объекты Характеристики объектов (переменные, исследова по которым производится разделение ния на кластеры) (возрастн Развлечени Спец. Спокойный Спорт ые группы я предложения отдых туристов) 17 -18 лет 19 -24 года ……. . 65 -70 лет Таб. 2 Конкретизированные переменные

Схема определения оптимального числа кластеров. • ■ На этапе 1 мы определяем количество кластеров на основании математического метода, основанного на коэффициенте агломерации. • ■ На этапе 2 мы проводим кластеризацию респондентов по полученному числу кластеров и затем строим линейное распределение по образованной новой переменной. Здесь также следует определить, сколько кластеров состоят из статистически значимого количества респондентов. В общем случае рекомендуется устанавливать минимально значимую численность кластеров на уровне не менее 10 респондентов. • ■ Если все кластеры удовлетворяют данному критерию, переходим к завершающему этапу кластерного анализа: интерпретации кластеров. Если есть кластеры с незначимым числом составляющих их наблюдений, устанавливаем, сколько кластеров состоят из значимого количества респондентов. • ■ Пересчитываем процедуру кластерного анализа, указав в диалоговом окне «Сохранить» число кластеров, состоящих из значимого количества наблюдений. • ■ Строим линейное распределение по новой переменной. • Описываем объекты, входящие в кластеры.

• Меню «Данные» – «Файл разбиения» • Выбрать опцию «Организовать вывод по группам» • Группы образуются по фактору – Метод Уорда • Анализ – описательные статистики- переносим все переменные кластеризации , выбираем опцию «Среднее значение» .

Пример: • В ходе исследования было опрошено 745 авиапассажиров, летавших одной из 22 российских и зарубежных авиакомпаний. Авиапассажиров просили оценить по пятибалльной шкале — от 1 (очень плохо) до 5 (отлично) — семь параметров работы наземного персонала авиакомпаний в процессе регистрации пассажиров на рейс: вежливость, профессионализм, оперативность, готовность помочь, регулирование очереди, внешний вид, работа персонала в целом.

• Требуется: • Сегментировать исследуемые авиакомпании по уровню воспринимаемого авиапассажирами качества работы наземного персонала. • Итак, у нас есть файл данных, который состоит из семи интервальных переменных, обозначающих оценки качества работы наземного персонала различных авиакомпаний (ql 3 -ql 9), представленные в единой пятибалльной шкале. Файл данных содержит одновариантную переменную q 4, указывающую выбранные респондентами авиакомпании (всего 22 наименования). Проведем кластерный анализ и определим, на какие целевые группы можно разделить данные авиакомпании.

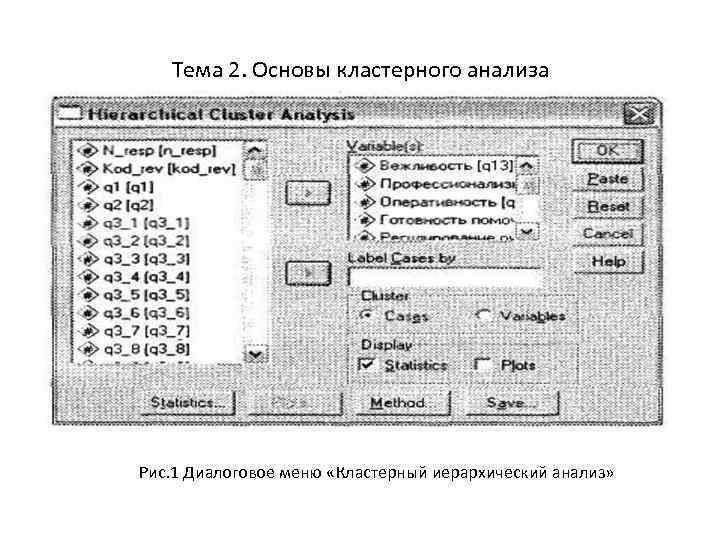Тема 2. Основы кластерного анализа Рис. 1 Диалоговое меню «Кластерный иерархический анализ»

Тема 2. Основы кластерного анализа Рис. 2 Диалоговое окно «Статистики» Выбираем вариант – «Принадлежности к кластерам нет»

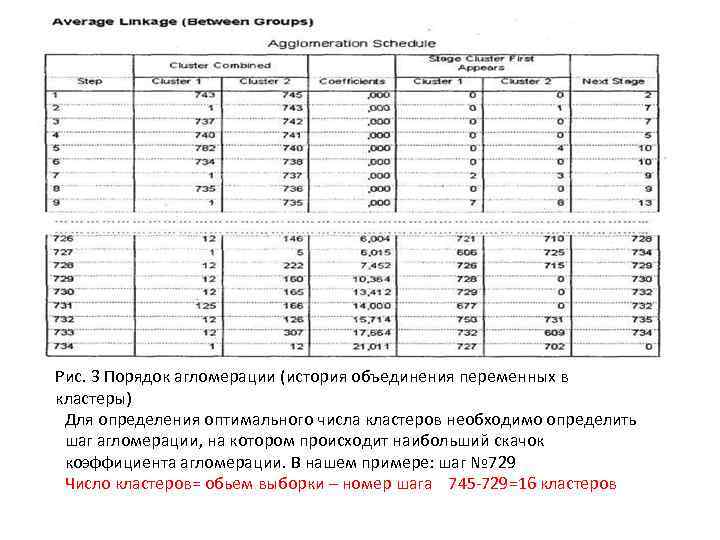Тема 2. Основы кластерного анализа Рис. 3 Порядок агломерации (история объединения переменных в кластеры) Для определения оптимального числа кластеров необходимо определить шаг агломерации, на котором происходит наибольший скачок коэффициента агломерации. В нашем примере: шаг № 729 Число кластеров= обьем выборки – номер шага 745 -729=16 кластеров

Тема 2. Основы кластерного анализа • В нашем случае коэффициенты плавно возрастают от 0 до 7, 452, то есть разница между коэффициентами на шагах с первого по 728 была мала (например, между 728 и 727 шагами — 0, 534). Начиная с 729 шага происходит первый существенный скачок коэффициента: с 7, 452 до 10, 364 (на 2, 912). Шаг, на котором происходит первый скачок коэффициента, — 729. Теперь, чтобы определить оптимальное количество кластеров, необходимо вычесть полученное значение из общего числа наблюдений (размера выборки). Общий размер выборки в нашем случае составляет 745 человек; следовательно, оптимальное количество кластеров составляет 745 -729 = 16.

Тема 2. Основы кластерного анализа Рис. 4 Диалоговое окно «Сохранить» кластерного анализа

Тема 2. Основы кластерного анализа Рис. 5 Диалоговое окно «Выбор метода кластеризации Выбираем метод Уорда!

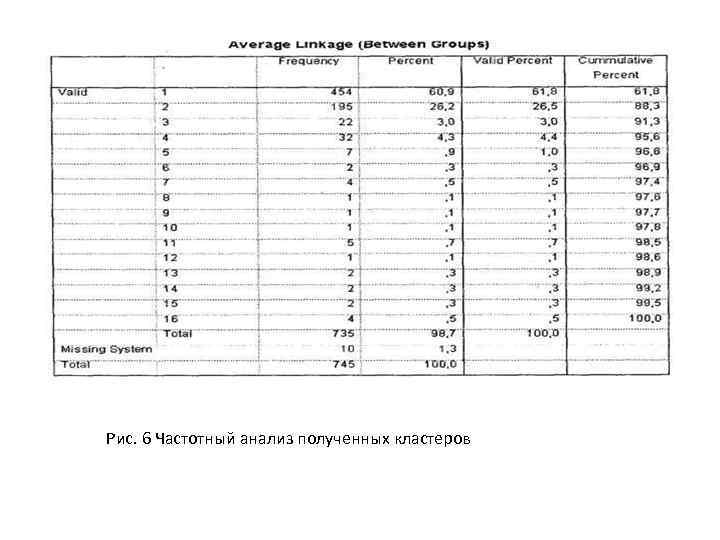Тема 2. Основы кластерного анализа Рис. 6 Частотный анализ полученных кластеров

• Как видно на рис. , в кластерах с номерами 5 -16 число респондентов составляет от 1 до 7. Наряду с вышеописанным универсальным методом определения оптимального количества кластеров (на основании разности между общим числом респондентов и первым скачком коэффициента агломерации) существует также дополнительная • рекомендация: размер кластеров должен быть статистически значимым и практически приемлемым. При нашем размере выборки такое критическое значение можно установить хотя бы на уровне 10. Мы видим, что под данное условие попадают лишь кластеры с номерами 1 -4. Поэтому • теперь необходимо пересчитать процедуру кластерного анализа с выводом четырехкластерного решения (будет создана новая переменная du 4_l).

Построив линейное распределение по вновь созданной переменной du 4_l, мы увидим, что только в двух кластерах (1 и 2) число респондентов является практически значимым. Нам необходимо снова перестроить кластерную модель — теперь для двухкластерного решения. После этого построим распределение по переменной du 2_l. Как видно из таблицы, двухкластерное решение имеет статистически и практически значимое число респондентов в каждом из двух сформированных кластеров: в кластере 1 — 695 респондентов; в кластере 2 — 40.

Рис. 7 Частотный анализ переменных в кластерах

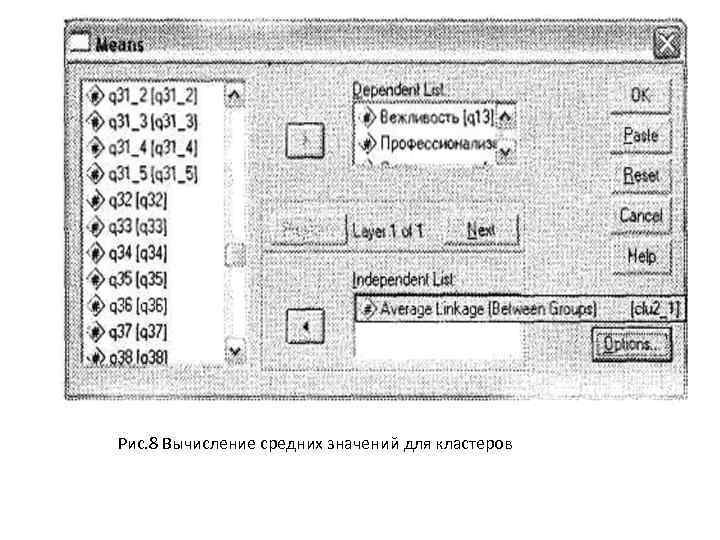Рис. 8 Вычисление средних значений для кластеров

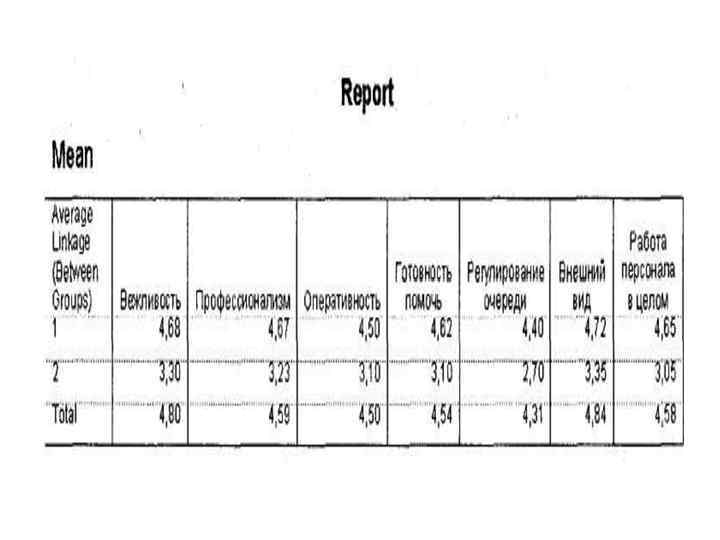
• Мы идентифицировали два значимых кластера, различающиеся по уровню средних оценок по критериям сегментирования. Теперь можно присвоить метки полученным кластерам: • для 1 — Авиакомпании, удовлетворяющие требованиям респондентов (по семи анализируемым критериям); • для 2 — Авиакомпании, не удовлетворяющие требованиям респондентов. • Теперь можно посмотреть, какие конкретно авиакомпании (закодированные в переменной q 4) удовлетворяют требованиям респондентов, а какие — нет по критериям сегментирования. Для этого следует построить перекрестное распределение • переменной q 4 (анализируемые авиакомпании) в зависимости от кластеризующей переменной clu 2_l.

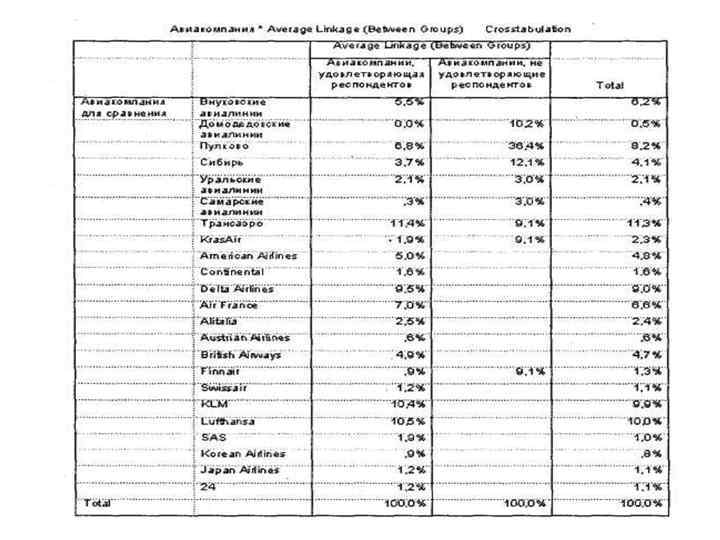Тема 2. Основы кластерного анализа

КОНДЖОИНТ-АНАЛИЗ

Конджоинт-анализ - метод для определения самого лучшего набора атрибутов, представляющих продукт или услугу. Цель конджоинт-анализа - измерение степени предпочтения потребителем одного из конкурирующих продуктов (услуг) в условиях предположения о комплексной оценке всех атрибутов, составляющих продукт.

Задачи, решаемые с помощью применения конджоинт-анализа: • Определить наилучшую (оптимальную) конфигурацию свойств продукта или услуги • Произвести сравнение свойств (атрибутов) продуктов с целью выявления тех из них, которые оказывают наибольшее влияние на покупательские решения. • Достоинством метода является возможность выявить латентные факторы, влияющие на поведение потребителей. • Сегментация рынка на основе потребительских предпочтений, например, оценка размера сегмента, отдающего предпочтение сервису, либо сегмента, чувствительного в первую очередь к цене, и т. д. Подобная информация позволяет выбрать наиболее привлекательные сегменты рынка и разработать стратегию работы с выбранными сегментами

Примеры • Выбор оптимальной конфигурации товара: например, поиск “компромисса” между количеством и сложностью встроенных функций комнатного кондиционера и показателями потребления кондиционером электроэнергии. • Выбор оптимального сочетания цены и размера упаковки для любого товара рынка FMCG • Определение значимости атрибутов товаров или услуг: изучение приоритетов потребителей по ключевым атрибутам товаров или услуг, например, сервис, цены, имидж, качество, широта ассортимента для розничной сети.

Пример в рамках курсовой работы У оператора мобильной связи имеется несколько тарифов, отличающихся по таким характеристикам, как стоимость звонков внутри и вне сети, стоимость смс и ммс сообщений, стоимость различных интернет-услуг, наличие включенных пакетов и дополнительных бонусов. По результатам опроса потребителей с помощью применения процедуры конджоинт анализа необходимо: • Определить, какие отличительные характеристики оказывают наибольшее влияние на выбор потребителя; • Составить профиль оптимального тарифа; • Выбрать тариф оператора, наиболее близкий к оптимальному и сформулировать управленческое решение.

Последовательность действий (в теории) - 1 Необходимо определить внешний вид упаковки нового шампуня, которая будет наиболее благосклонно воспринята покупателями. 1. Выделить характеристики, по которым различаются упаковки шампуней: - объем упаковки, - форма упаковки, - основной цвет тюбика, - рисунок / цвет рисунка, - материал, из которого изготовлена упаковка, - размер крышки и т. д. 2. ВЫБРАТЬ НАИБОЛЕЕ ВАЖНЫЕ ХАРАКТЕРИСТИКИ и для каждой их характеристик составить список всех возможных значений фактора: АТРИБУТЫ (ФАКТОРЫ) объем упаковки форма упаковки основной цвет тюбика материал, из которого изготовлена упаковка • • УРОВНИ АТРИБУТОВ (ЗНАЧЕНИЯ ФАКТОРОВ) 100 мл 150 мл с острыми краями с закругленными краями белый голубой пластик стекло Каждый из этих наборов значений факторов называется ПРОФИЛЕМ например, пластиковая овальная бутылка объемом 150 мл белого цвета. Задача – определить оптимальный профиль, наиболее предпочитаемый потребителями.

Последовательность действий (в теории) - 2 3. Опрос потребителей. По представленному визуализированному представлению всех полученных профилей респондентам необходимо проранжировать их в порядке убывания привлекательности (отдать предпочтения или назначить ранги) – измеряем вероятность покупки, степень предпочтения, вероятность рекомендации данного товара и т. д. 4. Качественный анализ полученных данных – с помощью процедуры совместного (конджоинт) анализа в программе IBM SPSS определить наиболее важные для респондентов характеристики упаковки. Количественный анализ полученных данных - с помощью процедуры совместного (конджоинт) анализа в программе IBM SPSS составить оптимальный для потребителя профиль упаковки шампуня.

Ограничения • Участники эксперимента должны быть действительными или потенциальными пользователями исследуемого товара или услуги. • Конджоинт-анализ невозможно применять для оценки товаров, атрибуты которых взаимосвязаны либо если товар или услуга не могут быть подвергнуты декомпозиции до элементарных атрибутов. • «Сложные» товары, то есть обладающие большим количеством значимых для принятия решений атрибутов, могут генерировать слишком большое количество альтернатив, так что респондент оказывается не в состоянии обработать настолько большое число вариантов

Процедура в SPSS (1) 1) Создание ортогонального плана или списка возможных профилей товара Открыть пустой документ в SPSS Данные – ортогональный план – генерировать Задаем имя фактора (например, объем) и его значения (100 мл – 1, 150 мл – 2). Атрибуты (факторы) Объем упаковки Форма упаковки Основной цвет тюбика Материал, из которого изготовлена упаковка Уровни атрибутов (значения факторов) 100 мл 150 мл С острыми краями С закругленными краями Белый Голубой Пластик Код Стекло 2 1 2 1

Процедура в SPSS (2) 2) Опрос респондентов и формирование файла с результатами опроса 3) Проведение процедуры конджоинтанализа в SPSS - написание скрипта Файл – Создать – Синтаксис После написания скрипта: Запуск - все

Процедура в SPSS (3) • CONJOINT • PLAN = 'C: UsersОльгаDesktopОртогональный шампуни. sav' • /DATA = 'C: UsersОльгаDesktopДанные шампуни. sav' • /SUBJECT = Респондент • /RANK = Шампунь_1 to Шампунь_8 • /PLOT = all • /PRINT = all • /UTILITY = 'C: UsersОльгаDesktopШампуни результаты. sav'.

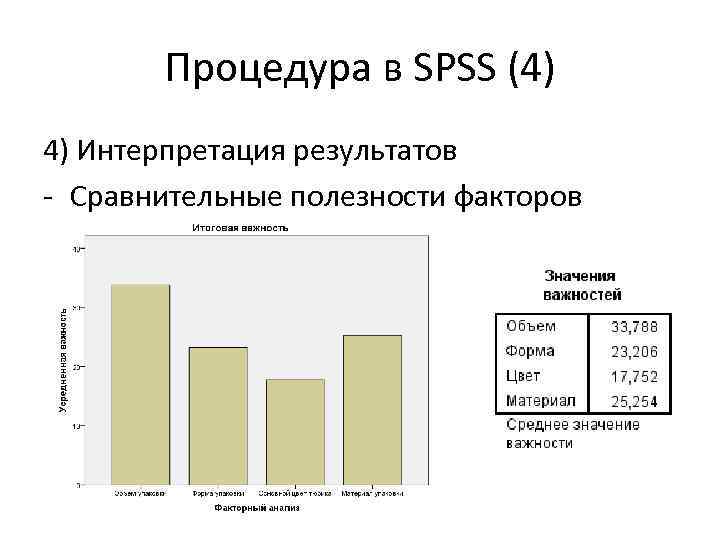Процедура в SPSS (4) 4) Интерпретация результатов - Сравнительные полезности факторов

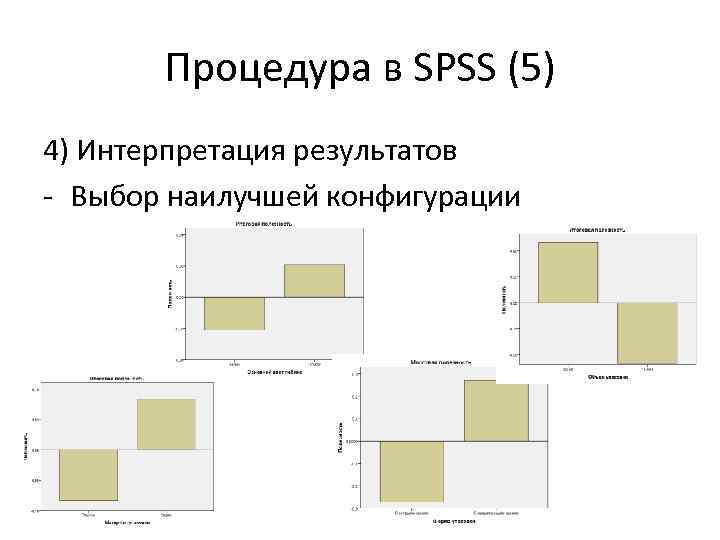Процедура в SPSS (5) 4) Интерпретация результатов - Выбор наилучшей конфигурации

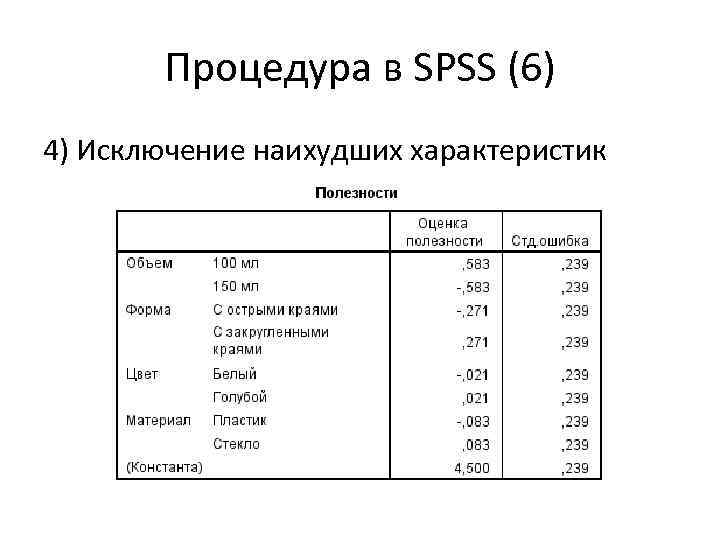Процедура в SPSS (6) 4) Исключение наихудших характеристик