Spring 2015 Principles to Actions Ensuring Mathematical Success

Spring 2015 Principles to Actions: Ensuring Mathematical Success For All NC DPI Mathematics Department

Welcome “Who’s in the Room”

Norms • Listen as an Ally • Value Differences • Maintain Professionalism • Participate Actively

maccss. ncdpi. wikispaces. net

A 25 -year History of Standards-Based Mathematics Education Reform

Standards Have Contributed to Higher Achievement • The percent of 4 th graders scoring proficient or above on NAEP rose from 13% in 1990 to 42% in 2013. • The percent of 8 th graders scoring proficient or above on NAEP rose from 15% in 1990 to 36% in 2013. • Between 1990 and 2012, the mean SAT-Math score increased from 501 to 514 and the mean ACT-Math score increased from 19. 9 to 21. 0.

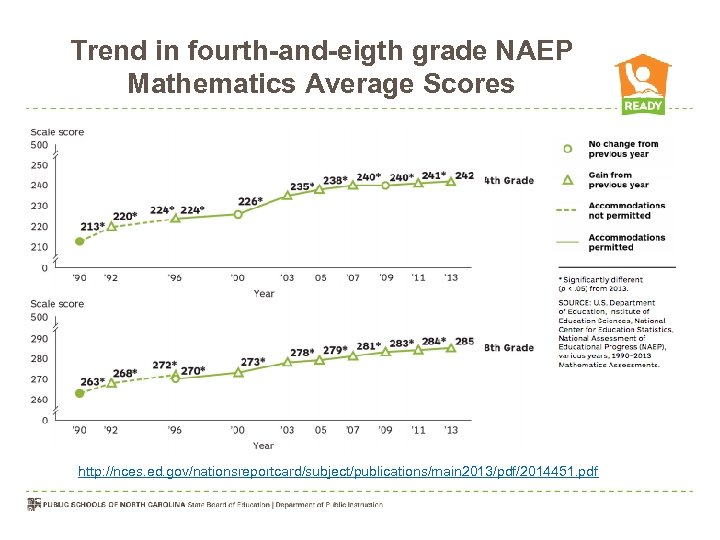Trend in fourth-and-eigth grade NAEP Mathematics Average Scores http: //nces. ed. gov/nationsreportcard/subject/publications/main 2013/pdf/2014451. pdf

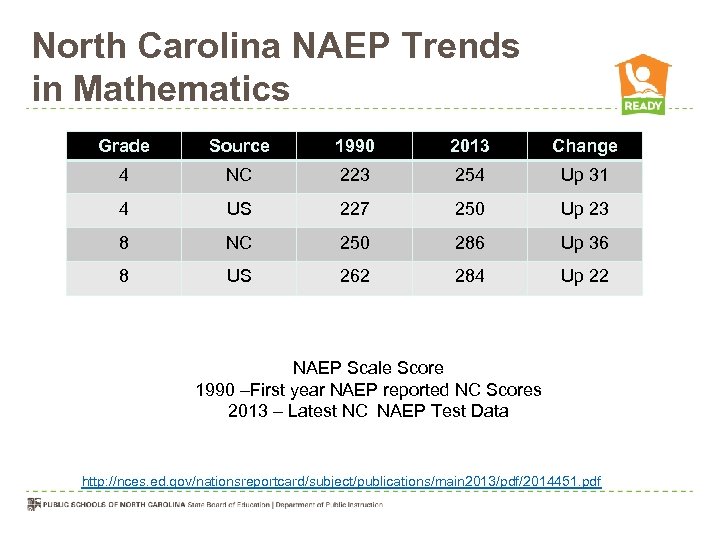North Carolina NAEP Trends in Mathematics Grade Source 1990 2013 Change 4 NC 223 254 Up 31 4 US 227 250 Up 23 8 NC 250 286 Up 36 8 US 262 284 Up 22 NAEP Scale Score 1990 –First year NAEP reported NC Scores 2013 – Latest NC NAEP Test Data http: //nces. ed. gov/nationsreportcard/subject/publications/main 2013/pdf/2014451. pdf

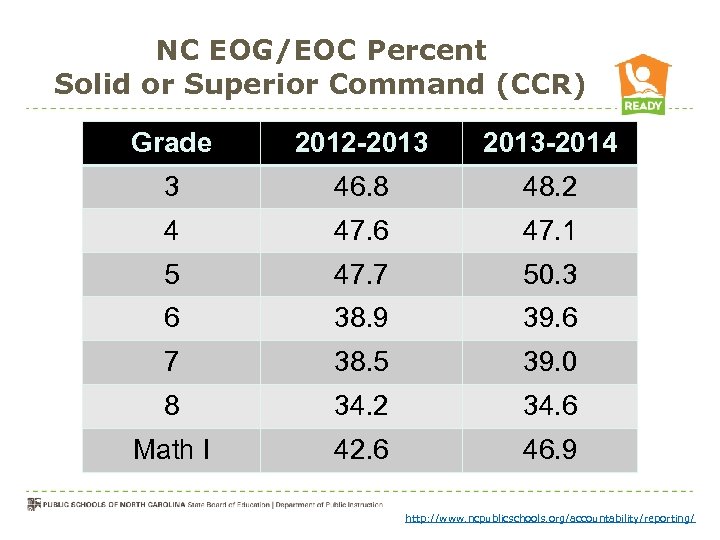NC EOG/EOC Percent Solid or Superior Command (CCR) Grade 2012 -2013 -2014 3 46. 8 48. 2 4 47. 6 47. 1 5 47. 7 50. 3 6 38. 9 39. 6 7 38. 5 39. 0 8 34. 2 34. 6 Math I 42. 6 46. 9 Common Core State Standards http: //www. ncpublicschools. org/accountability/reporting/

Although We Have Made Progress, Challenges Remain • The average mathematics NAEP score for 17 -year -olds has been essentially flat since 1973. • Among 34 countries participating in the 2012 Programme for International Student Assessment (PISA) of 15 -year-olds, the U. S. ranked 26 th in mathematics. • While many countries have increased their mean scores on the PISA assessments between 2003 and 2012, the U. S. mean score declined. • Significant learning differentials remain.

Brainstorm Administrators & Leadership Family Students Beliefs about Teaching and Learning Teachers Media Community

Principles to Actions: Ensuring Mathematical Success for All The primary purpose of Principles to Actions is to fill the gap between the adoption of rigorous standards and the enactment of practices, policies, programs, and actions required for successful implementation of those standards. NCTM. (2014). Principles to Actions: Ensuring Mathematical Success for All. Reston, VA: NCTM.

Principles to Actions: Ensuring Mathematical Success for All The overarching message is that effective teaching is the non-negotiable core necessary to ensure that all students learn mathematics. The six guiding principles constitute the foundation of Pt. A that describe highquality mathematics education. NCTM. (2014). Principles to Actions: Ensuring Mathematical Success for All. Reston, VA: NCTM.

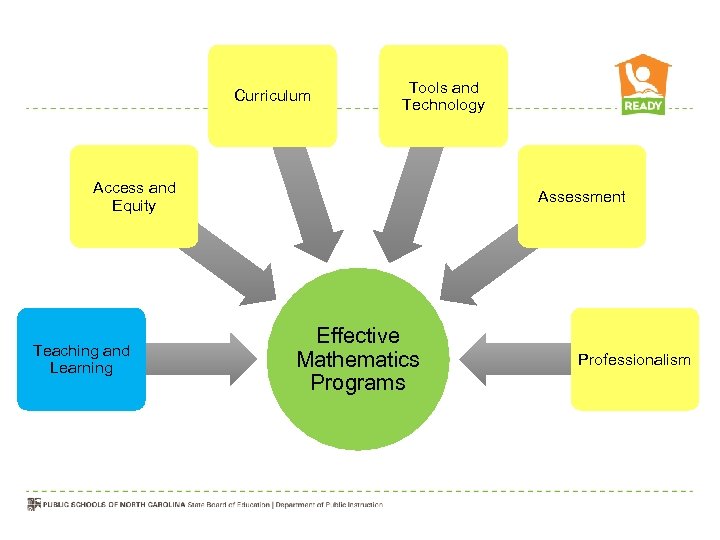Curriculum Tools and Technology Access and Equity Teaching and Learning Assessment Effective Mathematics Programs Professionalism

Teacher Beliefs “Teachers’ beliefs influence the decisions they make about the manner in which they teach mathematics. ” Principles to Actions pg. 10

Beliefs About Teaching and Learning Mathematics Students’ beliefs influence their perception of what it means to learn mathematics and how they feel toward the subject Principles to Actions pg. 10

High-Quality Standards are Necessary, But Insufficient, for Effective Teaching and Learning Teaching mathematics requires specialized expertise and professional knowledge that includes not only knowing mathematics but knowing it in ways that will make it useful for the work of teaching. Ball and Forzani 2010

For Each of the Six Principles • Obstacles to Implementing the Principle • Productive and Unproductive Beliefs • Overcoming the Obstacles • Illustration • Moving to Action

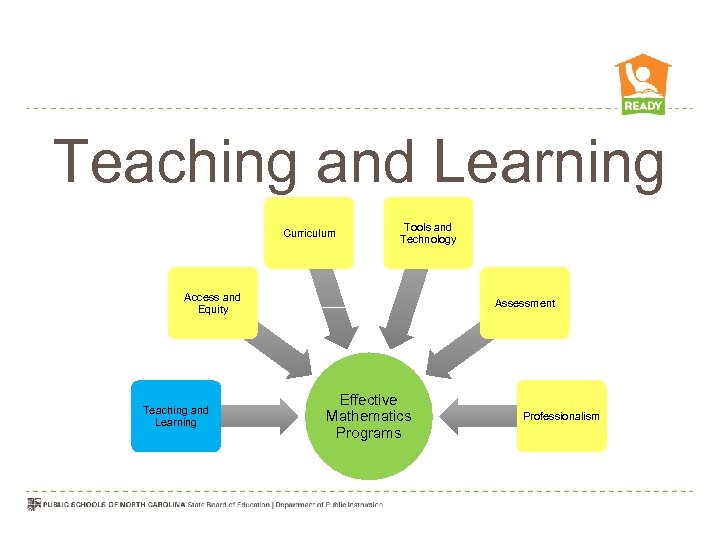Teaching and Learning Curriculum Tools and Technology Access and Equity Teaching and Learning Assessment Effective Mathematics Programs Professionalism

Teaching and Learning An excellent mathematics program requires effective teaching that engages students in meaningful learning through individual and collaborative experiences that promote their ability to make sense of mathematical ideas and reason mathematically. Principles to Actions pg. 7

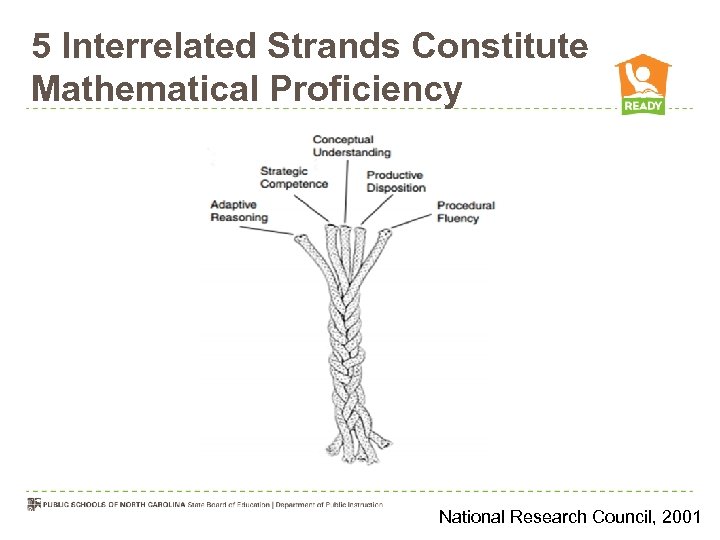5 Interrelated Strands Constitute Mathematical Proficiency National Research Council, 2001

Obstacles to Implementing High-Leverage Instructional Practices Dominant cultural beliefs about the teaching and learning of mathematics continue to be obstacles to consistent implementation of effective teaching and learning in mathematics classrooms.

Eight High-Leverage Instructional Practices 1. Establish mathematics goals to focus learning 2. Implement tasks that promote reasoning and problem solving 3. Use and connect mathematical representations 4. Facilitate meaningful mathematical discourse 5. Pose purposeful questions 6. Build procedural fluency from conceptual understanding 7. Support productive struggle in learning mathematics 8. Elicit and use evidence of student thinking

Not to be confused with…

What do you notice?

Overview of the Eight Mathematics Teaching Practices

1. Establish mathematics goals to focus learning. Effective teaching of mathematics establishes clear goals for the mathematics that students are learning, situates goals within learning progressions, and uses goals to guide instructional decisions. Principles to Actions pg. 12

Need 3 Volunteers per group for Role Playing • Choose a puzzle piece from the center of the table. • Find your group members. • In your group, role play the scenario on pgs 14 -15. • What do you notice about the dialog?

What did you notice about the dialog? Math coach intentionally shifts the conversation to a discussion of the mathematical ideas and learning that will be the focus of instruction

Principles to Action – pg. 16

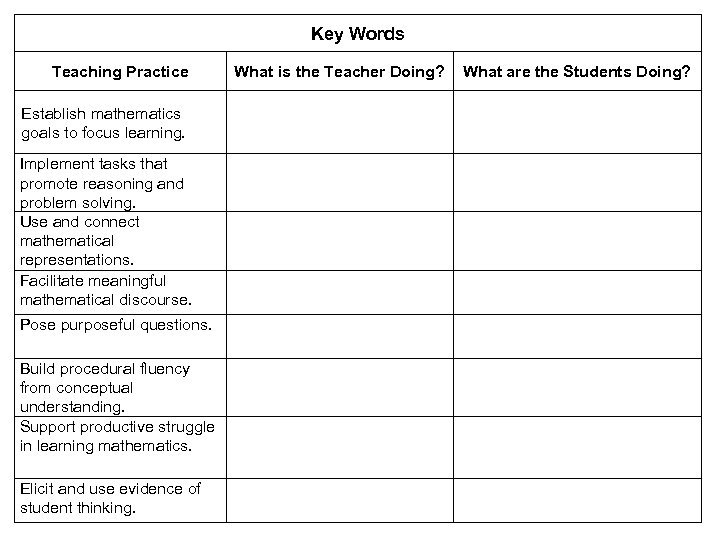
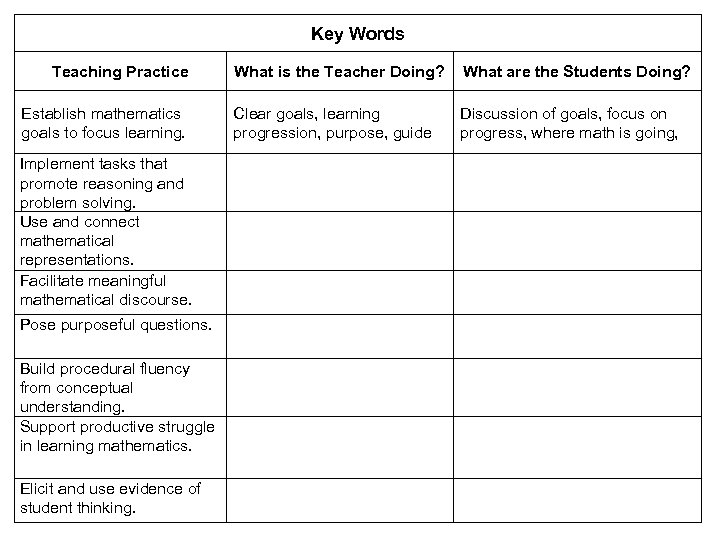Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing? Clear goals, learning progression, purpose, guide Discussion of goals, focus on progress, where math is going,

1. Establish Mathematics Goals to Focus Learning • Learning progressions or trajectories describe how students make transitions from prior knowledge to more sophisticated understandings • Both teachers and students need to be able to answer these crucial questions: – – What mathematics is being learned? Why is this important? How does it relate to what has already been learned? Where are these mathematical ideas going? • Situating learning goals within the mathematical landscape supports opportunities to: – Build explicit connections – See how ideas build and relate to one another – Develop a coherent and connected view of the discipline

2. Implement Tasks That Promote Reasoning and Problem Solving Effective teaching of mathematics engages students in solving and discussing tasks that promote mathematical reasoning and problem solving and that allow for multiple entry points and varied solution strategies. Principles to Actions pg. 17

High or Low Cognitive Demanding Task? High Low

Cognitive Demand Jigsaw/Sort 1. Everyone grab a puzzle piece from your table. 2. Move to the designated spot in the room for your color. – Green: Memorization – Yellow: Procedures without Connections – Blue: Procedures with Connections – Red: Doing Mathematics 3. Read page 18 and summarize the description associated with your cognitive demand task type. Come to a shared understanding of the demand task and be prepared to share back at your table. 4. At your table, use the contents of the envelope to sort the tasks by cognitive demand.

Principles to Actions pg. 18

Table Talk What are the attributes of a mathematically strong task?

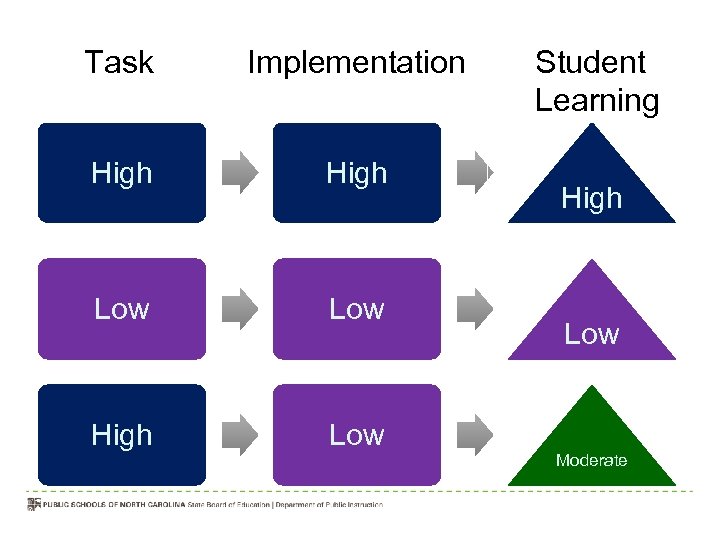Task Implementation High Low Student Learning High Low Moderate

Math Tasks There is no decision that teachers make that has a greater impact on students’ opportunities to learn and on their perception about what mathematics is than the selection or creation of the tasks with which the teacher engages students in shaping mathematics.

Look on page 21 NCDPI – Task http: //commoncoretasks. ncdpi. wikispaces. net/

Principles to Action - page 24

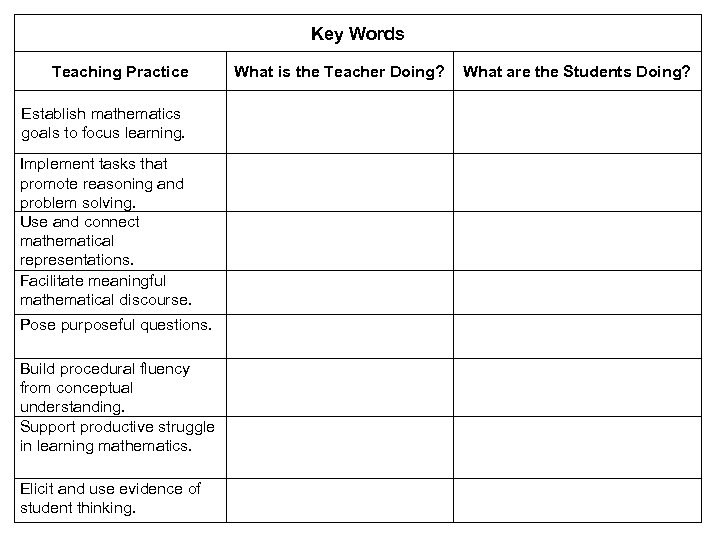
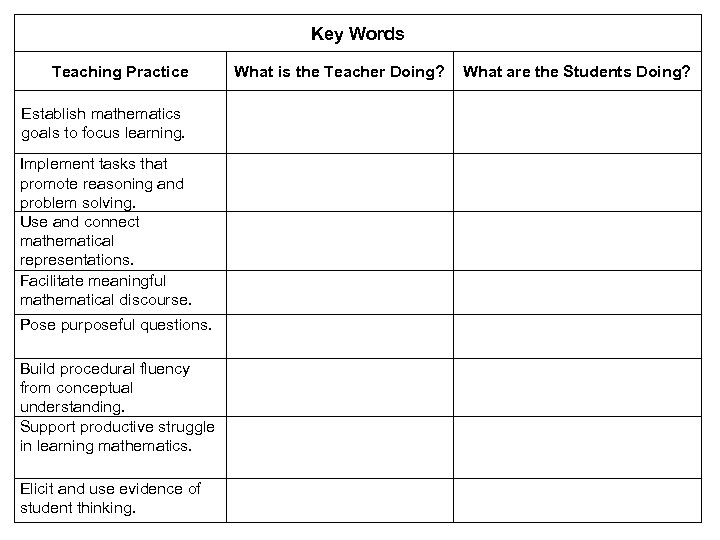Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

2. Implement tasks that promote reasoning and problem solving • Effective math teaching and learning uses carefully selected tasks as one way to motivate student learning and build new knowledge. • Research on math tasks over the past two decades has found: – Not all tasks provide the same opportunities for student thinking and learning. – Student learning is the greatest in classrooms where tasks consistently encourage high-level student thinking and the least in classrooms where tasks are routinely procedural in nature. – Tasks with high cognitive demands are the most difficult to implement well and are often transformed into less demanding tasks. • To ensure that students have the opportunity to engage in high- level thinking, teachers must regularly select and implement tasks the promote reasoning and problem solving.

3. Use and connect mathematical representations Effective teaching of mathematics engages students in making connections among mathematical representations to deepen understanding of mathematics concepts and procedures and as tools for problem solving. Principles to Actions pg. 24

Let’s Do Some Math! The third grade class is responsible for setting up the chairs for the spring band concert. In preparation, the class needs to determine the total number of chairs that will be needed and ask the school’s engineer to retrieve that many chairs from the central storage area. The class needs to set up 7 rows of chairs with 20 chairs in each row, leaving space for a center aisle. How many chairs does the school’s engineer need to retrieve from the central storage area? Principles to Actions pg. 27

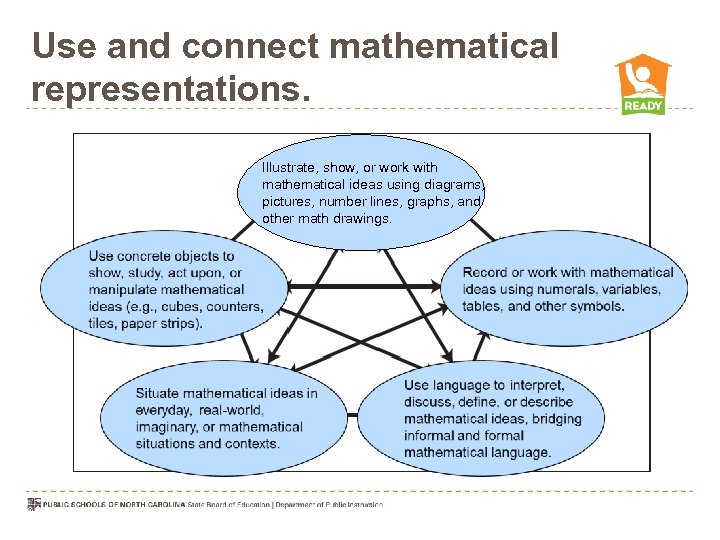Use and connect mathematical representations. Illustrate, show, or work with mathematical ideas using diagrams, pictures, number lines, graphs, and other math drawings.

Principles to Actions pg. 29

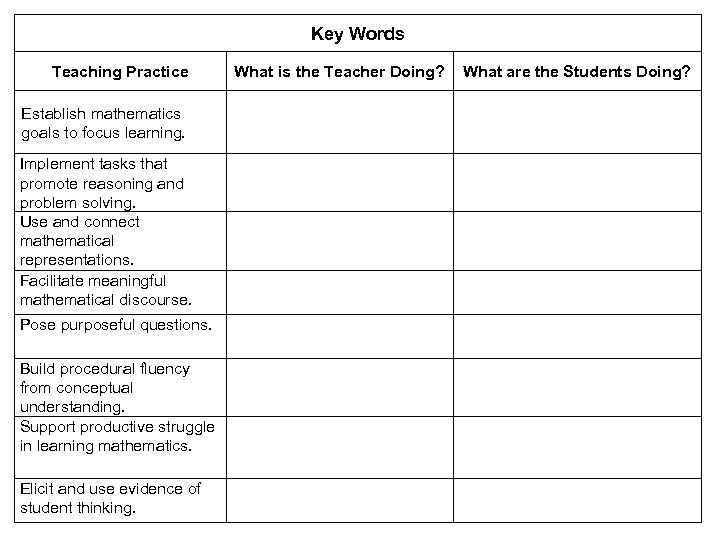Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

3. Use and Connect Mathematical Representations • Effective mathematics teaching includes a strong focus on using varied mathematical representations. • Using a variety of representations helps students examine a concept through more than one lens. Selected representations could include: – – – Visual representations Physical representations Symbolic representations Contextual representations Verbal representations • When students learn to represent, discuss, and make connections among mathematical ideas in multiple forms, they demonstrate deeper mathematical understanding and enhanced problem-solving skills. (Fuson, Kalchman, & Bransford, 2005; Lesh, Post, and Behr, 1987)

4. Facilitate meaningful mathematical discourse Effective teaching of mathematics facilitates discourse among students in order to build shared understanding of mathematical ideas by analyzing and comparing student approaches and arguments. Principles to Actions pg. 29

“What students learn is intertwined with how they learn it. And the stage is set for the how of learning by the nature of classroom-based interactions between and among teacher and students. ” (Smith & Stein, 2011)

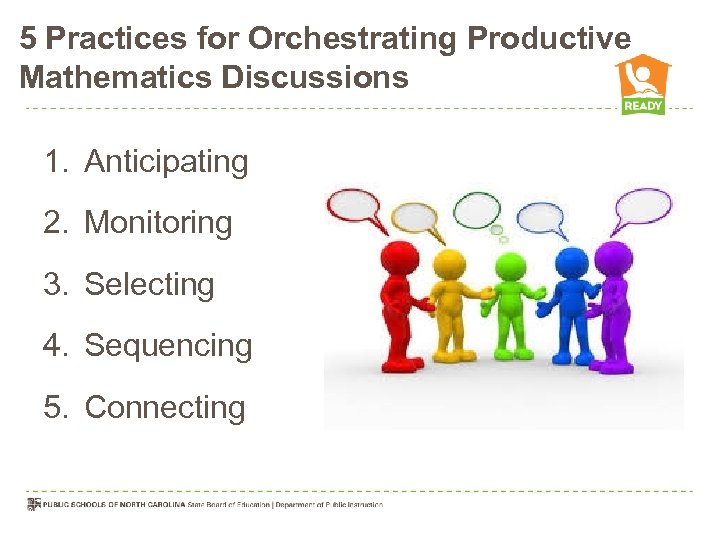5 Practices for Orchestrating Productive Mathematics Discussions 1. Anticipating 2. Monitoring 3. Selecting 4. Sequencing 5. Connecting

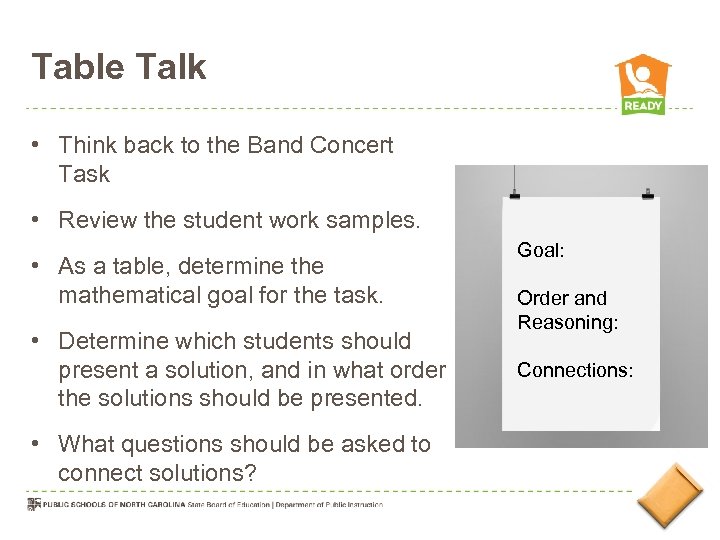Table Talk • Think back to the Band Concert Task • Review the student work samples. • As a table, determine the mathematical goal for the task. • Determine which students should present a solution, and in what order the solutions should be presented. • What questions should be asked to connect solutions? Goal: Order and Reasoning: Connections:

Principles to Actions pg. 35

Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

4. Facilitate Meaningful Discourse • Effective mathematics teaching engages students in discourse to advance the mathematical learning of the whole class. • Smith and Stein (2011) describe five practices for effectively using student responses in class discussions: – – – Anticipating student responses prior to the lesson Monitoring students’ work on engagement with tasks Selecting particular students to present their mathematical work Sequencing students’ responses in specific order for discussion Connecting different students’ responses and connecting responses to key mathematical ideas • Students must have opportunities to talk with, respond to, and question one another as part of the discourse community, in ways that support the mathematics learning for all students in class

5. Pose purposeful questions Effective teaching of mathematics uses purposeful questions to assess and advance student reasoning and sense making about important mathematical ideas and relationships. Principles to Actions pg. 35

Types of Questions-Four Corners Gathering Information Probing Thinking Making the mathematics visible Encouraging reflection and justification

Types of Questions • In your table group, sort the question descriptions and examples. • Create at least 1 additional question that fits each description. • Are these types of questions important in the classroom? Principles to Actions pg. 36 -37

Funneling vs Focusing • Read pg 37, last two paragraphs • Review Figure 16 on pg 39 -40 • Using chart paper, illustrate funneling vs focusing questioning patterns. • What are some barriers that might prevent teachers from moving from funneling to focusing questions?

Principles to Actions pg. 41

Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

5. Pose Purposeful Questions • Effective mathematics teaching relies on questions that encourage students to explain and reflect on their thinking as an essential component of meaningful discourse. • Commonalities exist across a number of questioning frameworks. Key cross cutting aspects of a number of frameworks that are particularly important within mathematics instruction include: – Gathering information • Students recall facts, definitions, or procedures – Probing thinking • Students explain, elaborate, or clarify their thinking, including articulating the steps in solution methods or the completing of a task – Making the mathematics visible • Students discuss mathematical structures and make connections among mathematical ideas and relationships – Encouraging reflection and justification • Students reveal deeper understanding of their reasoning and actions, including making an argument for the validity of their work

6. Build procedural fluency from conceptual understanding Effective teaching of mathematics builds fluency with procedures on a foundation of conceptual understanding so that students, over time, become skillful in using procedures flexibly as they solve contextual and mathematical problems. Principles to Actions pg. 42

Form two lines… • How does computational fluency relate to conceptual understanding? • How do we move from conceptual understanding to computational fluency? • Where do we use computational fluency in mathematics? • Why are algorithms necessary?

How could Anna’s reasoning help David understand his mistake? Principles to Actions pg. 43

How Are these Methods Interrelated? Principles to Actions pg. 45

http: //maccss. ncdpi. wikispaces. net/Elementary+Webinars

Principles to Action - page 47

Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

6. Build Fluency from Conceptual Understanding • Effective mathematics teaching focuses on the development of both conceptual understanding and procedural fluency. • Both NCTM and CCSS-M emphasize that procedural fluency follows and builds on a foundation of conceptual understanding, strategic reasoning, and problem solving. • Students who use math effectively do much more than carry out procedures. Such students must also know: – Which procedure is appropriate and most productive for a given situation, – What a given procedure accomplishes, and – What kind of results to expect • “Mechanical execution of procedures without understanding their conceptual basis often leads to bizarre results” (Martin, (2009), p. 165)

7. Support productive struggle in learning mathematics Effective teaching of mathematics consistently provides students, individually and collectively, with opportunities and supports to engage in productive struggle as they grapple with mathematical ideas and relationships. Principles to Actions pg. 48

Teachers greatly influence how students perceive and approach struggle in the mathematics classroom. Even young students can learn to value struggle as an expected and natural part of learning. Principles to Actions pg. 50

Shopping Trip Task Joseph went to the mall with his friends to spend the money that he had received for his birthday. When he got home, he had $24 remaining. He had spent 3/5 of his birthday money at the mall on video games and food. How much money did he spend? How much money had he received for his birthday? Principles to Actions pg. 51

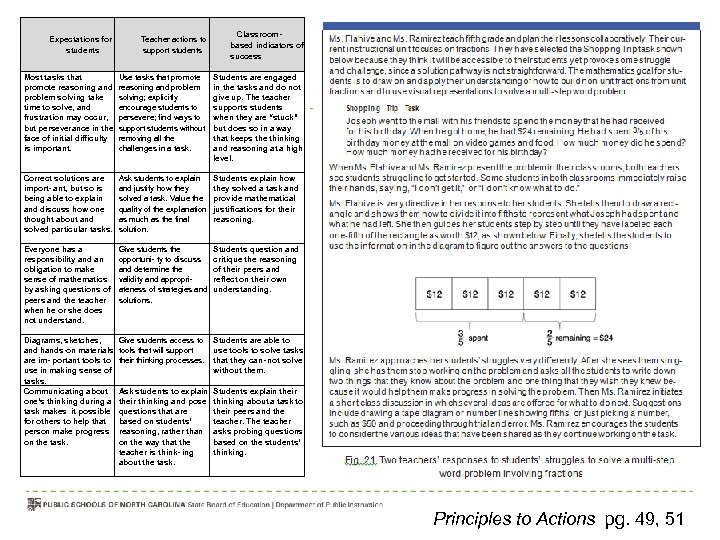Classroombased indicators of success Expectations for students Teacher actions to support students Most tasks that promote reasoning and problem solving take time to solve, and frustration may occur, but perseverance in the face of initial difficulty is important. Use tasks that promote reasoning and problem solving; explicitly encourage students to persevere; find ways to support students without removing all the challenges in a task. Students are engaged in the tasks and do not give up. The teacher supports students when they are “stuck” but does so in a way that keeps the thinking and reasoning at a high level. Correct solutions are import- ant, but so is being able to explain and discuss how one thought about and solved particular tasks. Ask students to explain and justify how they solved a task. Value the quality of the explanation as much as the final solution. Students explain how they solved a task and provide mathematical justifications for their reasoning. Everyone has a responsibility and an obligation to make sense of mathematics by asking questions of peers and the teacher when he or she does not understand. Give students the opportuni- ty to discuss and determine the validity and appropri- ateness of strategies and solutions. Students question and critique the reasoning of their peers and reflect on their own understanding. Diagrams, sketches, and hands-on materials are im- portant tools to use in making sense of tasks. Communicating about one’s thinking during a task makes it possible for others to help that person make progress on the task. Give students access to Students are able to tools that will support use tools to solve tasks their thinking processes. that they can- not solve without them. Ask students to explain their thinking and pose questions that are based on students’ reasoning, rather than on the way that the teacher is think- ing about the task. Students explain their thinking about a task to their peers and the teacher. The teacher asks probing questions based on the students’ thinking. Principles to Actions pg. 49, 51

Fixed vs. Growth Mindset • Fixed: those who believe intelligence is an innate trait; believe that learning should come naturally • Growth: those who believe intelligence can be developed through effort; likely to persevere through struggle because they see challenging work as an opportunity to learn and grow Principles to Actions pg. 50

Struggling to Learn Carol Dweck, Psychologist Growth Mind-set Research The Teaching Channel How does having a growth mindset relate to embracing and supporting student struggle?

Principles to Actions pg. 53

Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

Emergentmath. com

7. Support Productive Struggle in Learning Mathematics • • • Effective mathematics instruction supports students in struggling productively as they learn mathematics. Teacher actions to support students in productive struggle include: – Students engage in problems that take time to solve • Teachers select tasks that promote reasoning and problem solving; explicitly encouraging students to persevere; finding ways to support students without removing challenges in a task. – Students explain and discuss how they thought about and solved tasks • Teachers ask students to explain and justify how they solved a task, and value the quality of the explanation as much as the final solution. – Students have a responsibility and obligation to make sense of the math • Teachers give students the opportunity to discuss and determine the validity and appropriateness of strategies and solutions. – Students use important tools in making sense of the task • Teachers give students access to tools that will support their thinking process. – Students communicate one’s thinking during a task • Teachers ask students to explain their thinking and pose questions based on students’ reasoning, rather than on the way the teacher is think about the task.

8. Elicit and use evidence of student thinking Effective teaching of mathematics uses evidence of student thinking to assess progress toward mathematical understanding and to adjust instruction continually in ways that support and extend learning. Principles to Actions pg. 53

Preparation of each lesson needs to include intentional and systematic plans to elicit evidence that will provide “a constant stream of information about how student learning is evolving toward the desired goal. ” Principles to Actions pg. 53

“My Favorite No: Learning From Mistakes” During the video; • Identify strategies the teacher uses to access, support, and extend student thinking. • How do these strategies allow for immediate re-teaching? • What student behaviors were associated with these instructional strategies?

Principles to Actions pg. 56

Key Words Teaching Practice Establish mathematics goals to focus learning. Implement tasks that promote reasoning and problem solving. Use and connect mathematical representations. Facilitate meaningful mathematical discourse. Pose purposeful questions. Build procedural fluency from conceptual understanding. Support productive struggle in learning mathematics. Elicit and use evidence of student thinking. What is the Teacher Doing? What are the Students Doing?

Which Math Practices would students be engaged in?

8. Elicit and Use Evidence of Student Thinking • • • Effective mathematics teaching elicits evidence of student’s current mathematical understanding and uses it as the basis for making instructional decisions. A focus on evidence includes: – Identifying indicators of what is important to notice in students’ mathematical thinking – Planning for ways to elicit that information – Interpreting what the evidence means with respect to students’ learning – Deciding how to respond on the basis of students’ understanding Using assessment for learning means that: – Students are revealing their mathematical understanding, reasoning, and methods in classroom discourse and written work. – Students reflect on mistakes and misconceptions to improve their understanding – Students ask questions, responding to, and giving suggestions to support the learning of their classmates – Students assess and monitor their own progress towards math learning goals, and identify areas they can improve

Sort the Beliefs Unproductive Beliefs Check your arrangement on Principles to Actions pg. 11

Beliefs About Teaching and Learning Mathematics Principles to Action – pg. 11

Essential Elements of Effective Mathematics Programs Curriculum Tools and Technology Access and Equity Teaching and Learning Assessment Effective Mathematics Programs Professionalism

Start Small, Build Momentum, and Persevere The process of creating a new cultural norm characterized by professional collaboration, openness of practice, and continual learning and improvement can begin with a single team of grade-level or subject-based mathematics teachers making the commitment to collaborate on a single lesson plan.

Principles to Actions What action are you taking? • Your role: – Leaders and policymakers pgs 110 -112 – Principals, coaches, specialists, other school leaders pgs 112 -114 – Teachers pgs 114 -117 • Choose at least one action that you plan to implement as a result of today’s session. • Turn and share your plan with a shoulder partner.

What questions do you have?

Follow Us! NC Mathematics www. facebook. com/North. Carolina. Mathematics @ncmathematics http: //maccss. ncdpi. wikispaces. net

DPI Mathematics Section Kitty Rutherford Elementary Mathematics Consultant 919 -807 -3841 kitty. rutherford@dpi. nc. gov Denise Schulz Elementary Mathematics Consultant 919 -807 -3839 denise. schulz@dpi. nc. gov Lisa Ashe Secondary Mathematics Consultant 919 -807 -3909 lisa. ashe@dpi. nc. gov Vacant Secondary Mathematics Consultant 919 -807 -3842 Dr. Jennifer Curtis K – 12 Mathematics Section Chief 919 -807 -3838 jennifer. curtis@dpi. nc. gov Susan Hart Mathematics Program Assistant 919 -807 -3846 susan. hart@dpi. nc. gov

For all you do for our students!