SPRING 2010 REVIEW SESSION FOR SECOND 3330 MIDTERM

SPRING 2010 REVIEW SESSION FOR SECOND 3330 MIDTERM Jehan-François Pâris jfparis@sbcglobal. net

Materials on the midterm • From Chapter IV—Computer Arithmetic – Floating-point operations • Whole Chapter V—Processor Architecture • From Chapter VI—Memory Hierarchy – Technology overview

General hints • You will be allowed to bring with you one 8. 5"× 11" one-sided sheet of notes • I like to ask – Short problems • Test how you can apply the materials – Questions about motivations, advantages and disadvantages

FLOATING POINT OPERATIONS

Hints • Focus on – Floating point number representation • Single and double precision • Exponent biases – Conversions – Addition, subtraction and multiplication – General organization of FP unit

Fractional binary numbers • 0. 1 is ½ or 0. 5 ten • 0. 01 is 0. 1 is 1/4 or 0. 25 ten • 0. 11 is ½ + ¼ = ¾ or 0. 75 ten • 1. 1 is 1½ or 1. 5 ten • 10. 01 is 2 + ¼ or 2. 5 ten • 11. 11 is ______ or _____

Normalizing binary numbers • 0. 1 becomes 1. 0× 2 -1 • 0. 01 becomes 1. 0× 2 -2 • 0. 11 becomes 1. 1× 2 -1 • 1. 1 is already normalized and equal to 1. 0× 20 • 10. 01 becomes 1. 001× 21 • 11. 11 becomes 1______× 2_____

Representation • Sign + exponent + coefficient SExp Coefficient • IEEE Standard 754 – 1 + 8 + 23 = 32 bits – 1+ 11 + 52 = 64 bits (double precision)

The sign bit • 0 indicates a positive number • 1 a negative number

The exponent (I) • 8 bits for single precision • 11 bits for double precision • With 8 bits, we can represent exponents between -126 and + 127 – All-zeroes value is reserved for the zeroes and denormalized numbers – All-ones value are reserved for the infinities and Na. Ns (Not a Number)

The exponent (II) • Exponents are represented using a biased notation – Stored value = actual exponent + bias • For 8 bit exponents, bias is 127 – Stored value of 1 corresponds to – 126 – 0 and 255 are reserved for special Stored value of 254 corresponds to values +127

Special values (I) • Signed zeroes: – IEEE 754 distinguishes between +0 and – 0 – Represented by • Sign bit: 0 or 1 • Biased exponent: all zeroes • Coefficient: all zeroes

Special values (II) • Denormalized numbers: – Numbers whose coefficient cannot be normalized • Smaller than 2– 126 – Will have a coefficient with leading zeroes and exponent field equal to zero • Reduces the number of significant digits

Special values (III) • Infinities: – + and – – Represented by • Sign bit: 0 or 1 • Biased exponent: all ones • Coefficient: all zeroes

Special values (IV) • Na. N: – For Not a Number – Often result from illegal divisions: 0/0, ∞/∞, ∞/–∞, –∞/∞, and –∞/–∞ – Represented by • Sign bit: 0 or 1 • Biased exponent: all ones • Coefficient: non zero

The coefficient • Also known as fraction or significand • Most significant bit is always one – Implicit and not represented 001… 1000000000000 • Biased exponent is 127 ten • True coefficient is implicit one followed by all zeroes

Decoding a floating point number • Sign indicated by first bit • Subtract 127 from biased exponent to obtain power of two: – 127 • Use coefficient to construct a normalized binary value with a binary point: 1. • Number being represented is 1. × 2 – 127

First example 001… 0 000000000000000 • Sign bit is zero: Number is positive • Biased exponent is 126 Power of two is-1 • Normalized binary value is 1 1. 0000000 • Number is 1× 2 -1 = ½

Second example 110… 0 1100000000000000 • Sign bit is one: Number is negative • Biased exponent is 128 Power of two is 1 • Normalized binary value is 1. 1100000 • Number is -1. 11× 21 = -11. 1 = -3. 5 ten

Encoding a floating point number • Use sign to pick sign bit • Normalize the number: Convert it to form 1. × 2 • Add 127 to exponent to obtain biased exponent • Coefficient is equal to fractional part of number

First example • Represent 5: – Convert to binary: 101 – Normalize: 1. 01× 22 – Sign bit is 0 – Biased exponent is 127 + 2 = 10000001 two – Coefficient is 0100… 0 0 0100000000000000 10… 01

Second example • Represent – 3/4 – Convert to binary: 0. 11 – Normalize: 1. 1× 2 -1 – Sign bit is 1 – Biased exponent is 127 -1 = 01111110 two – Coefficient is 10… 0 1 100000000000000 01… 10

Guard bits • Do all arithmetic operations with two additional bits to reduce rounding errors

Double precision arithmetic • Use 64 -bit double words – One bit for sign – Eleven bits for exponent • 2, 048 possible values • Exponent bias is 1023 – Fifty-two bits for coefficient • Plus the implicit leading bit

Encoding and decoding • Same procedures as for single precision – Remember that exponent bias is now 1, 203

If that is now enough, … • Can use 128 -bit quad words • Allows us to have – One bit for sign – Fifteen bits for exponent • From – 16382 to +16383 – One hundred twelve bits for coefficient • Plus the implicit leading bit

Binary floating point addition (I) • Say 1001 + 10 or 1. 001× 23 + 1. 0× 21 • Denormalize number with smaller exponent: 1. 001× 23 + 0. 01× 23 • Add the numbers: 1. 001× 23 + 0. 01× 23 = 1. 011× 23 • Result is normalized

Binary floating point addition (II) • Say 101 + 11 or 1. 01× 22 + 1. 1× 21 • Denormalize number with smaller exponent: 1. 01× 22 + 0. 11× 22 • Add the numbers: 1. 01× 22 + 0. 11× 22 = 10. 00× 22 • Normalize the results 10. 00× 22 = 1. 000× 23

Binary floating point subtraction • Say 101 – 11 or 1. 01× 22 – 1. 1× 21 • Denormalize number with smaller exponent: 1. 01× 22 – 0. 11× 22 • Perform the subtraction: 1. 01× 22 – 0. 11× 22 = 0. 10× 22 • Normalize the results 0. 10× 22 = 1. 0× 21

Decimal floating point multiplication • Exponent of product is the sum of the exponents of multiplicand multiplier • Coefficient of product is the product of the coefficients of multiplicand multiplier • Compute sign using usual rules of arithmetic • May have to renormalize the product

Decimal floating point multiplication • 6× 103 + 2. 5× 102 = ? • Exponent of product is: 3+2=5 • Multiply the coefficients: 6 × 2. 5 = 15 • Result will be positive • Normalize the result: 15× 105 = 1. 5× 106

Binary floating point multiplication • Exponent of product is the sum of the exponents of multiplicand multiplier • Coefficient of product is the product of the coefficients of multiplicand multiplier • Compute sign using usual rules of arithmetic • May have to renormalize the product

Binary floating point multiplication • Say 110 × 11 or 1. 1× 22 × 1. 1× 21 • Exponent of product is: 2+1=3 • Multiply the coefficients: 1. 1 × 1. 1 = 10. 01 • Result will be positive • Normalize the result: 10. 01× 103 = 1. 001× 104

FP division • Very tricky • One good solution is to multiply the dividend by the inverse of the divisor That is all you need to know!

A trap • Addition does not necessarily commute: • – 9× 1037 + 4× 10 -37 • Observe that • (– 9× 1037 + 9× 1037) + 4× 10 -37 = 4× 10 -37 while • – 9× 1037 + (9× 1037+ 4× 10 -37) = 0 due to the limited accuracy of FP

IMPLEMENTATIONS

The floating-point unit • Floating-point instructions were an optional feature – User had to buy a separate floatingpoint unit aka floating point coprocessor • As a result, many processor architectures keep using separate banks of registers for integer arithmetic and floating point arithmetic

Why? • Having separate banks of integer and FP registers increases the number of registers without requiring an extra bit in the register address fields – Remain 5 bits for MIPS even though we now have 64 registers

Stack operations (I) • Three types of operations: – Loads store an operand on the top of the stack – Arithmetic and comparison operations find two operands of the top of the stack and replace them by the result of the operation – Stores move the top of stack register into memory

Example • a=b+c – Load b on top of stack – Load c on top of stack – Add c to b – Store result into a b --c b --b+c -----

Stack operations (II) • Instruction set also allowed – Operations on top of stack register and the ith register below – Immediate operands – Operations on top of stack register and a memory location • Poor performance of FP unit architecture motivated an extension to the x 86 instruction set

Review questions • How would you represent 0. 5 in double precision? • How would you convert this doubleprecision value into a single precision format? • When doing accounting, we could do all the computations in cents using integer arithmetic. What would we win? What would we lose?

PROCESSOR ARCHITECTURE Jehan-François Pâris jfparis@sbcglobal. net

Hints (I) • Focus on – Data paths followed by each class of instructions – Pipelining hazards IMPORTANT • Data hazards • Control hazards

Hints (II) • Focus on – Techniques used to reduce • Data hazards –Forwarding results • Troubles with. IMPORTANT ld instruction • Control hazards –Early decision for beq, bne instructions – Exceptions/interrupts

A "TOY" CPU

The subset • Will include – Load and store instructions: lw (load word) and sw (store word) – Arithmetic-logic instructions: add, sub, and, or and slt (set less than) – Branch instructions: beq (branch if equal) and j (jump)

Load and store instructions • Format I • Three operands: – Two registers r 1 and r 2 – One displacement d • lw r 1, d(r 2) loads into register r 1 main memory word at address contents(r 2) + d • sw r 1, d(r 2) stores contents of register r 1 into main memory word at address

Arithmetic-logic instructions • Format R • Three operands: – Three registers r 1, r 2 and r 3 • Store into register r 1 result of r 2 r 3 where can be add, subtract, and, or as well as set if less than

Branch instruction • Format I • Three operands: – Two registers r 1 and r 2 – One displacement d • beq, r 1, r 2, d set value of PC to PC+4 + 4×d iff r 1 = r 2

The simplest data path • Assume CPU will do nothing but – Incrementing its program counter and – Deliver the next instruction

The simplest data path 4 P C Instruction Memory Read address Instruction Add

Implementing R 2 R instructions • Takes two 32 -bit inputs • Returns – A 32 -bit output – A 1 -bit signal if the result is zero

The register file • Two read outputs that are always available • One write input activated by a Reg. Write signal • Three register selectors

The register file 5 5 5 Read select 1 Read data 1 Read select 2 Read data 2 Write select Write data Reg. Write: enables register writes

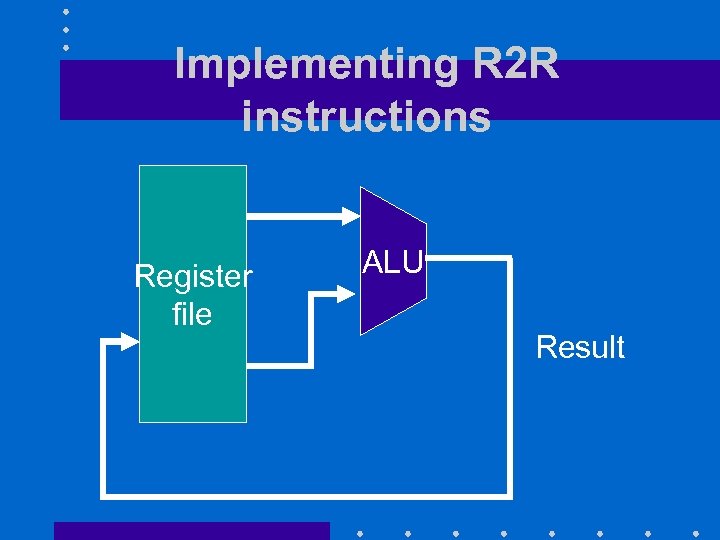Implementing R 2 R instructions Register file ALU Result

Implementing load and store • Require – Access to data memory – An address calculation: • contents(r 2) + d • Before doing this addition, we must transform 16 -bit displacement d into a 32 -bit value using sign extension

The data memory • • One address selector One write data input One read data output Two controls – Mem. Write – Mem. Read

Sign extension (I) • If 16 -bit number has a zero as MSB – It is positive – Must add 16 zero bits 0110 1010 0100 0000 1010 0100 0110

Sign extension (II) • If 16 -bit number has a one as MSB – It is negative – Must add 16 one bits 1110 1010 0100 1111 1010 0100 1110

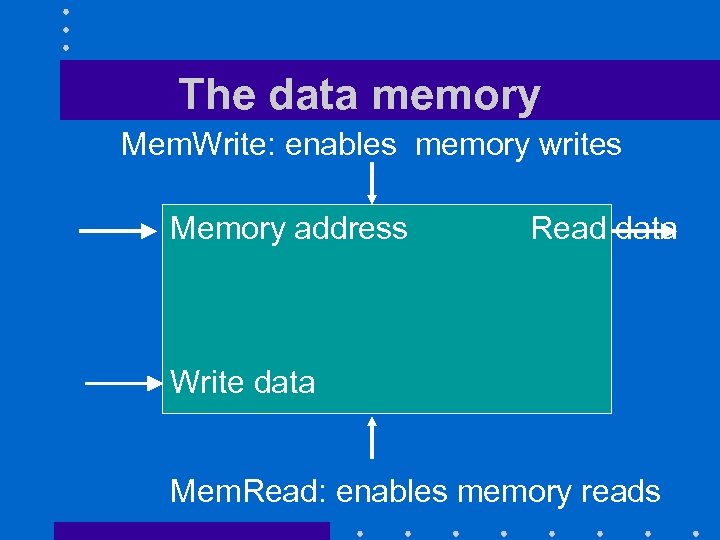The data memory Mem. Write: enables memory writes Memory address Read data Write data Mem. Read: enables memory reads

Implementing the store instruction Register file ALU Address Write Sign-extended offset Read

Implementing the load instruction Register file ALU Address Write Sign-extended offset Read

Implementing conditional branch • Target Address: – Sign-extend 16 -bit immediate part of instruction – Shift left 2 – Add to PC • Branch Control Logic: – Perform test operation on two registers

Implementing conditional branch PC+4 Shift left 2 Register file Sign-extended offset Add ALU Branch Destination To branch control logic

Note • Arithmetic-logic operations only use – Register file and ALU • Load and store use – ALU for computing memory address – Data memory

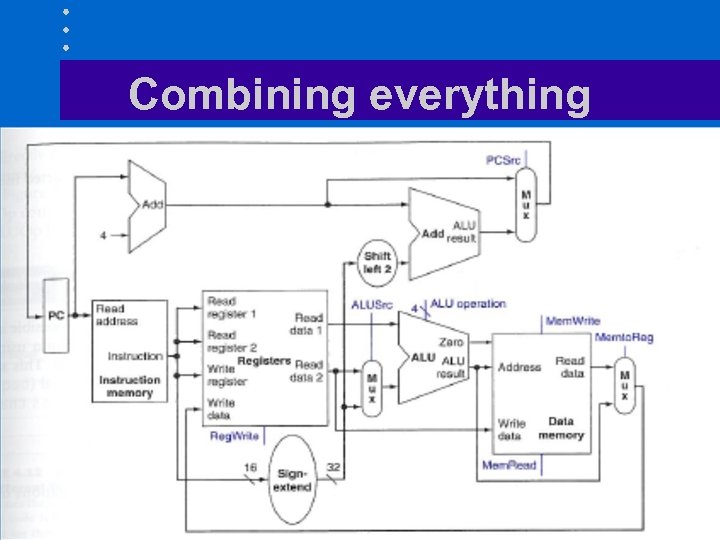Combining everything

Limitations of single-cycle design • If we want all instructions to be executed in one cycle – Clock cycle must be long enough to accommodate instruction taking the most time • Floating-point multiply or divide • Does not work for CPUs that have a rich instruction set

PIPELINING

Instruction steps (II) • Since MIPS instruction set has fixed fields, we can combine fetch and decode steps 1. Fetch instruction from memory 2. Read registers while decoding instruction 3. Execute register to register operation or calculate address 4. Access operand in memory

Step 1: Fetch and decode

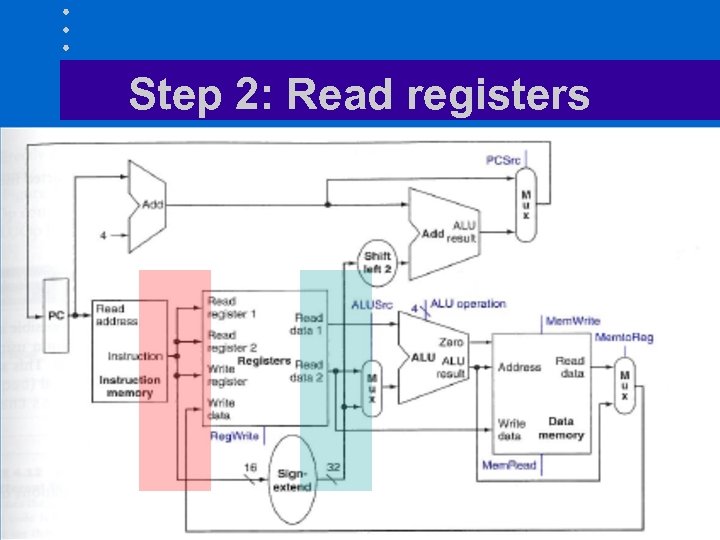Step 2: Read registers

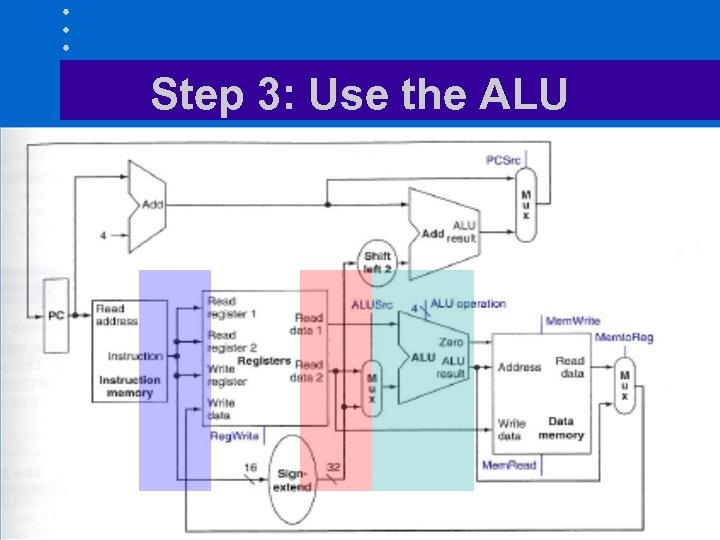Step 3: Use the ALU

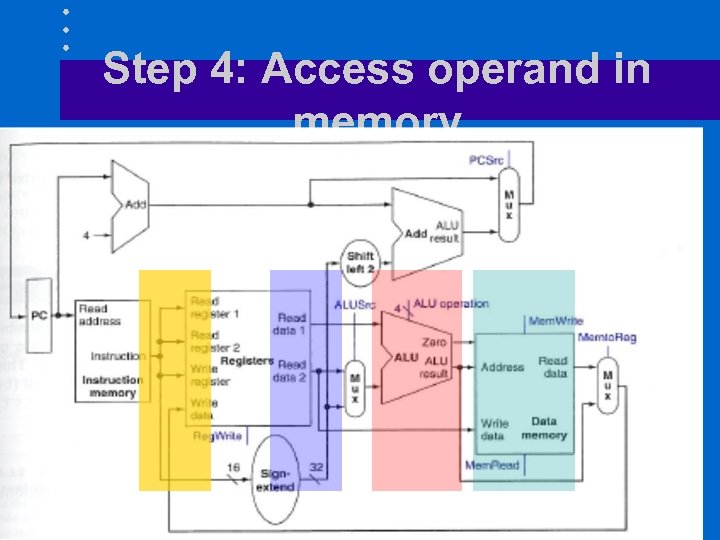Step 4: Access operand in memory

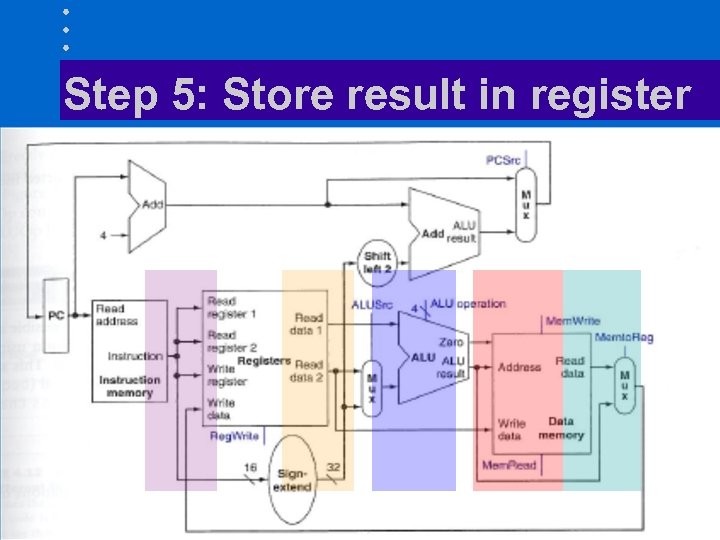Step 5: Store result in register

Observations • Most R format instructions operate on three registers and skip step 4 • Same for most I format instructions with an immediate operand • Store operations skip step 5 • Load register instructions go through all five steps

Pipelining limitations • Some instructions that skip a step will still have to wait until preceding instruction is done. • Hazards: – An instruction cannot proceed because • Hardware cannot support the combination of instructions (structural hazards)

A bad MIPS instruction (I) • We could think of a MIPS instruction with three registers operands ADDX r 1, r 2, r 3 adding to r 1 the contents of the word at address contents of r 2 + contents of r 3 • We would have r 1 = r 1 + Mem[r 2+r 3]

A bad MIPS instruction (II) • Adding this instruction would be a very bad idea – Why?

Answer • Instruction would require two steps using the ALU – Adding r 2 and r 3 to compute the address of the memory operand (step 4) – Adding the memory operand to r 1 • New step would introduce a structural hazard by preventing any other instruction to access the ALU

Data hazards (I) • Assume we have add $s 0, $t 1 sub $t 2, $s 0, $t 3 or s 0 = t 0 + t 1 t 2 = s 0 – t 3 • Need result of add before proceeding with sub instruction

Data hazards (II) • New value of $s 0 computed by the add instruction is not loaded in $s 0 until its step 5 has completed • Sub instruction must wait until add instruction has performed its step 5 before performing its step

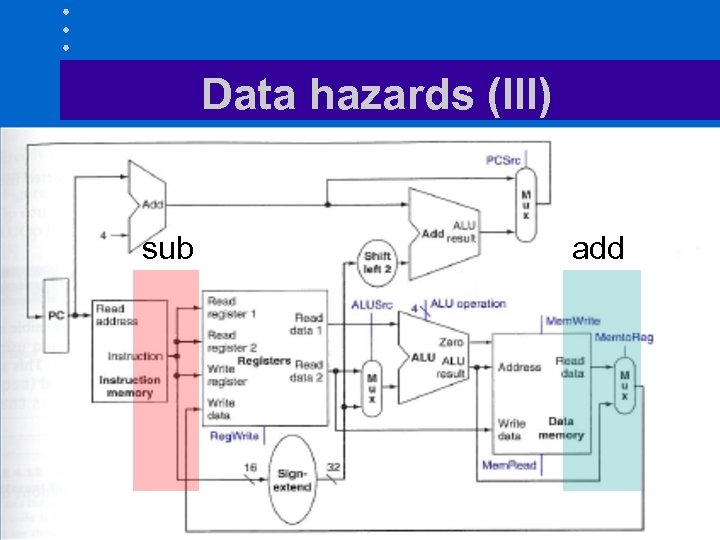Data hazards (III) sub add

Data hazards (IV) • We lose three cycles during which nothing the pipeline will be stalled • Cannot trust compiler to remove all data hazards • Observe that new value of $s 0 become available at the end of step 3 of add instruction – Add special circuitry to provide this value at the end of step 2 of sub

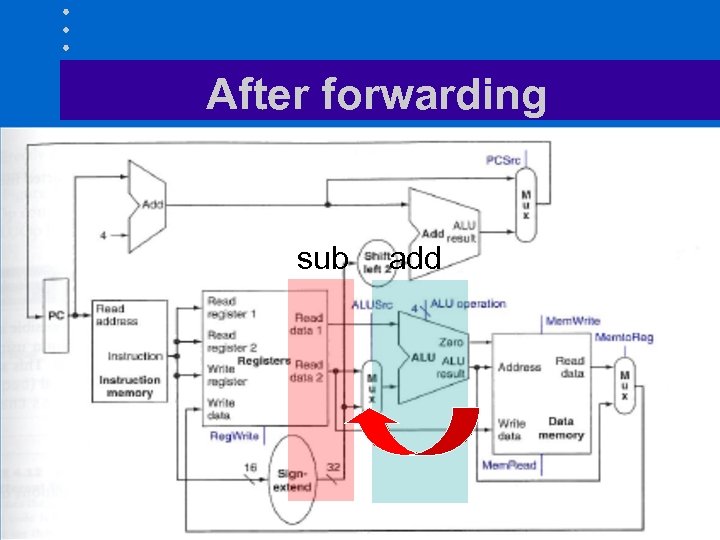After forwarding sub add

Limitations (I) • Assume we have lw $s 0, 20($t 1) sub $t 2, $s 0, $t 3 or s 0 = Mem[t 1+20] t 2 = s 0 – t 3 • Need new value of s 0 before proceeding with sub instruction

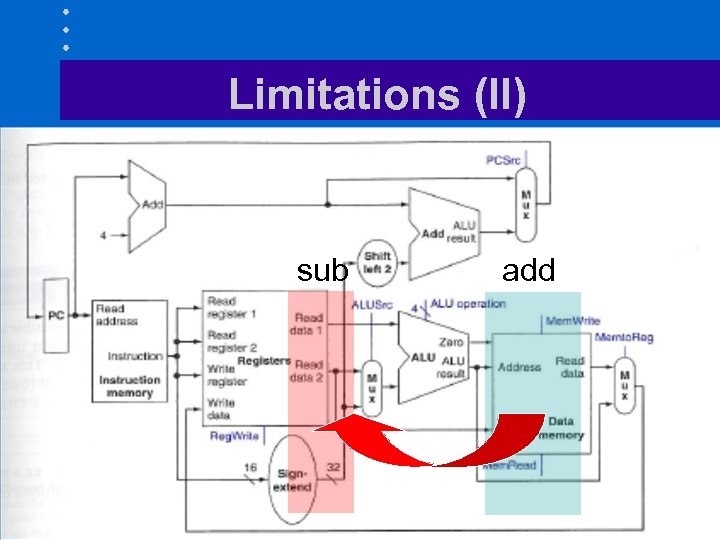Limitations (II) sub add

A last word • The MIPS architecture assumes that we have separate memories for instructions and data – Having a single memory for both would result in many more hazards

Control/jump hazards • Happen whenever we have a conditional jump • Consider the instructions add $4, $5, $6 beq $1, $2, 40 or $7, $8, $9 • Need result of conditional branch before deciding whether to execute next instruction

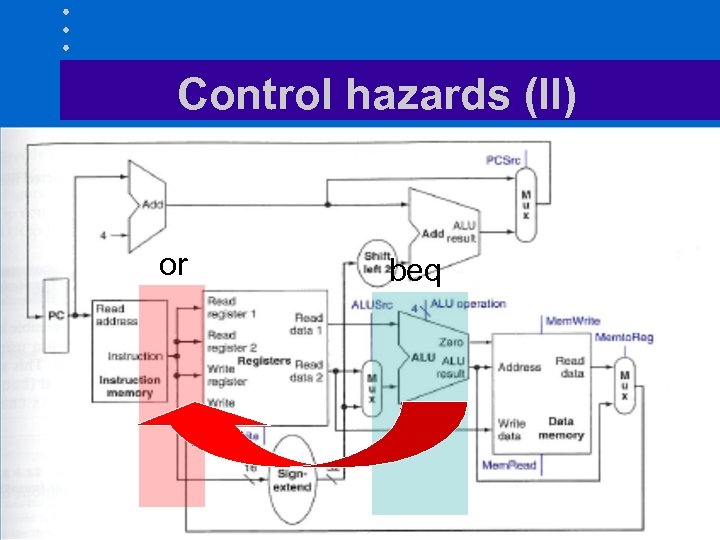Control hazards (II) or beq

Pipelined datapath

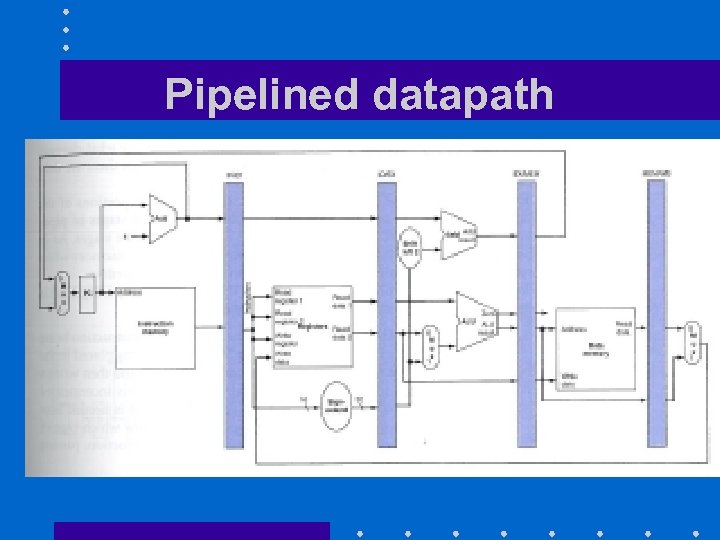
Datapaths for pipelined organization • Define five steps 1. Fetch instruction from memory (IF) 2. Instruction decode and register reads (ID) 3. Execute AL operation on ALU (EX) 4. Access operand in memory (MEM) 5. Write back results into a register (WB)

Datapaths for pipelined organization • Insert registers to save outputs of each step that are outputs of a the next step 1. IF/ID registers 2. ID/EX registers 3. EX/MEM registers 4. MEM/WB registers

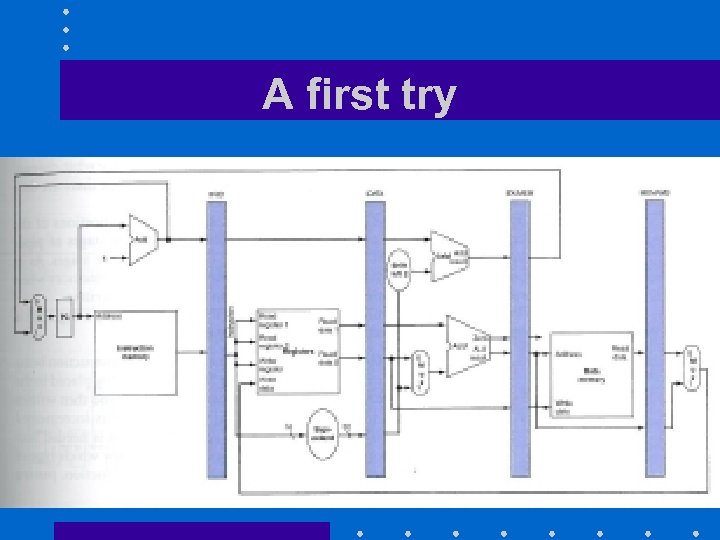A first try

Comments • This first try is not correct – Load instruction will not be implemented correctly • Address of destination register will be lost as soon as new instruction will be fetched • Must save it at each step

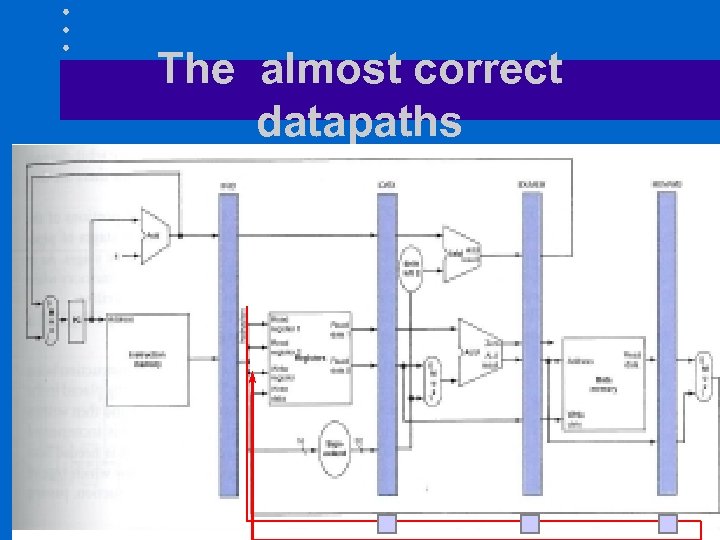The almost correct datapaths

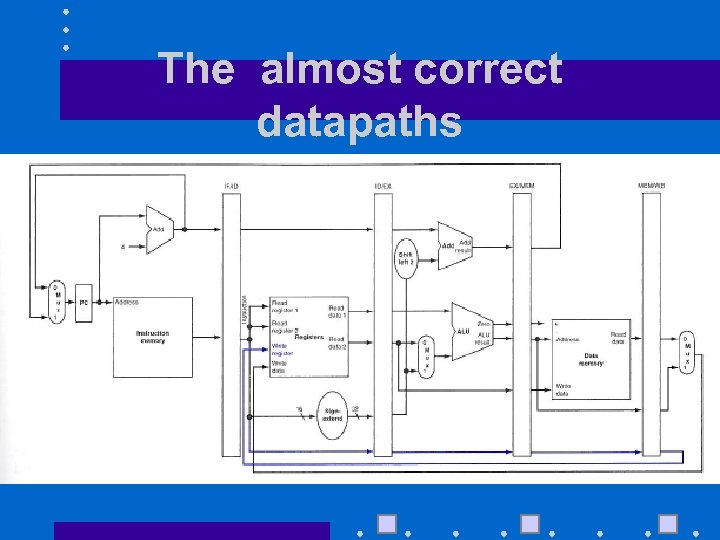The almost correct datapaths

More problems • Address of destination register is not always at the same place in all instructions – Could be instruction bits (20 -16) • For all I-format instructions that write into a register – Could be instruction bits (15 -11) • In R format instructions

Why? • In R format instructions opcodesource dest shamt funct • In I format instructions opcodesource s/d constant/address

The solution • Add a multiplexer at stage EX

More data hazards • We can forward the results of sub instruction at the end of its EX step – In time for all four following instructions • To do that we need special forwarding unit • Not all data hazards can be avoided – lw followed by any instruction accessing the loaded word

Data hazard detection unit • Detects hazards that cannot be avoided • Inserts no operation instructions (nop) – They do nothing!

More about control hazards • Outcome of conditional branch is not known until end of step EX – beq and bne use arithmetic unit to evaluate the branch condition – If branch is taken, we must abort the two following instructions • Easy because they have not yet updated anything

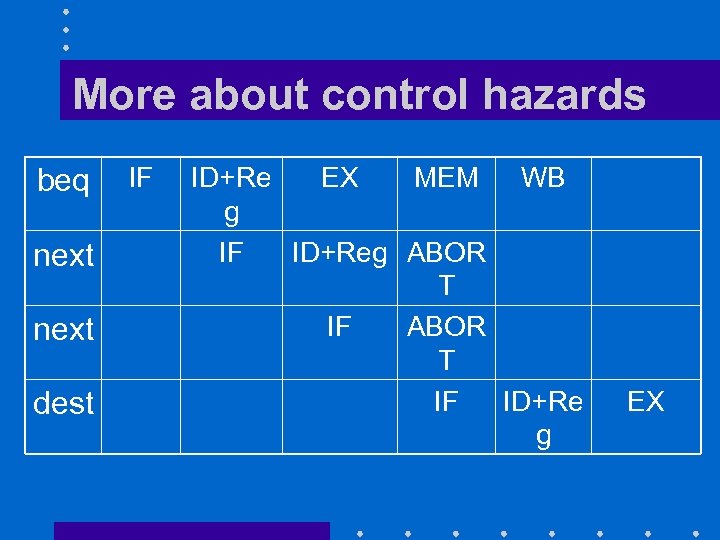More about control hazards beq next dest IF ID+Re EX MEM WB g IF ID+Reg ABOR T IF ID+Re g EX

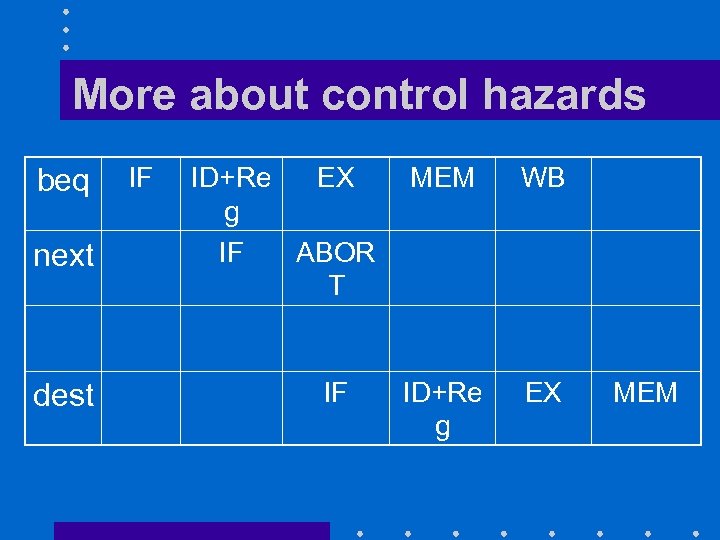More about control hazards beq next dest IF ID+Re EX g IF ABOR T IF MEM WB ID+Re g EX MEM

Better implementation of beq/bne

MIPS Optimization • Move comparison ahead to reduce the number of aborted instructions – Add a simple EQUAL/NOT EQUAL comparison hardware that tests outputs of register file • Bitwise XOR then ORing the results –Will return zero if the register contents are identical

EXCEPTIONS AND INTERRUPTS

Interrupts (I) • Request to interrupt the flow of execution the CPU • Detected by the CPU hardware – After it has executed the current instruction – Before it starts the next instruction.

Interrupts (II) • When an interrupt occurs: a) The current state of the CPU (program counter, program status word, contents of registers, and so forth) is saved, normally on the top of a stack b) A new CPU state is fetched

Interrupts (III) • New state includes a new hardwaredefined value for the program counter – Cannot “hijack” interrupts • Process is totally transparent to the task being interrupted – A process never knows whether it has been interrupted or not

Types of interrupts (I) • I/O completion interrupts – Notify the OS that an I/O operation has completed, • Timer interrupts – Notify the OS that a task has exceeded its quantum of CPU time,

Types of interrupts (II) • Traps – Notify the OS of a program error (division by zero, illegal op code, illegal operand address, . . . ) or a hardware failure • System calls – Notify OS that the running task wants to submit a request to the OS • Notification of another event

A surprising discovery • Programs do interrupt themselves!

MIPS Implementation (I) • Interrupts are a special case of a branch – Use same techniques for handling control hazards • Almost all MIPS interrupts jump to the same hardware address (x 80000180) – MIPS use a special register to pass along the type of interrupt to the interrupt handler • The Cause register

MIPS Implementation • MIPS also saves the address + 4 of the affected instruction in a special register – EPC register • A STATUS register allows selective disabling of interrupts – Useful for handling short critical sections in single-threaded kernel

Issues (I) • Interrupted instruction may have to be restarted – Typical for I/O completion interrupts • Must then maintain precise exceptions that accurately identify the instruction being interrupted – Not true for hardware interrrupts

Issues (II) • Must be able to restart instruction at the exact point it was interrupted – Not always easy on many architectures • MIPS solution is to roll back everything and restart instruction as if nothing had happened – Easier on MIPS since register/memory update is always the last step of any instruction

THE MEMORY HIERARCHY Jehan-François Pâris jfparis@sbcglobal. net

Hints • Focus on general characteristics – Access times – Transfer rates – Disk reliability issues as summarized here

Dynamic RAM • Standard solution for main memory since 70's – Replaced magnetic core memory • Bits represented stored on capacitors – Charged state represents a one • Capacitors discharge – Must be dynamically refreshed – Achieved by accessing each cell several thousand times each second

Magnetic disks Servo Platter Arm R/W head

Magnetic disks • Disk spins at a speed varying between – 5, 400 rpm (laptops) and – 15, 000 rpm (Seagate Cheetah X 15, …) – Accessing data requires • Positioning the head on the right track: –Seek time • Waiting for the data to reach the R/W head

Average rotational delay • What would be the average rotational delay of a hypothetical disk drive spinning at 12, 000 rpm 1. Convert to rotations per second: 12, 000 rpm = 200 Hz 2. Compute period 1/200 = 5 ms 3. Rotational delay is half period: 2. 5 ms

Overall performance • Disk access times are still dominated by rotational latency – Were 8 -10 ms in the late 70's when rotational speeds were 3, 000 to 3, 600 RPM • Disk capacities and maximum transfer rates have done much better – Pack much more tracks per platter – Pack much more bits per track

Reliability issues • Disk drives have more reliability issues than most other computer components – Moving parts eventually wear – Infant mortality – Would be too costly to produce perfect magnetic surfaces • Disks have bad blocks

Disk failure rates • Failure rates follow a bathtub curve – High infantile mortality – Low failure rate during useful life – Higher failure rates as disks wear out

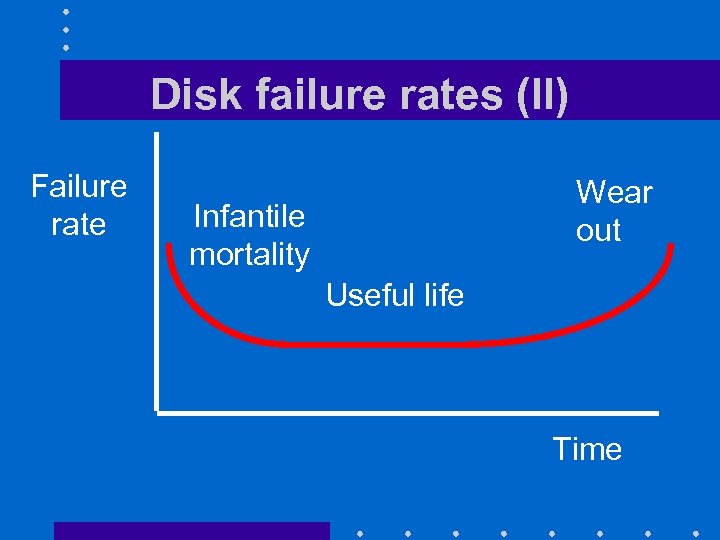Disk failure rates (II) Failure rate Wear out Infantile mortality Useful life Time

Disk failure rates (III) • Infant mortality effect can last for months for disk drives • Cheap ATA disk drives seem to age less gracefully than SCSI drives

MTTF • Disk manufacturers advertise very high Mean Times To Fail (MTTF) for their products – 500, 000 to 1, 000 hours, that is, 57 to 114 years • Does not mean that disk will last that long! • Means that disks will fail at an average rate of one failure per 500, 000 to

More MTTF Issues • Failure rates observed in the field are much higher than manufacturers claim – Can go up to 8 to 9 percent per year • Corresponding MTTFs are 11 to 12. 5 years

Problem • MTTF of a batch of disks is 20 years • What is the expected yearly failure rate for this batch of disks?

Solution • 1/20 = 5%

Bad blocks • Disk controller uses redundant encoding that can detect and correct many errors • When internal disk controller detects a bad block – Marks it as unusable – Remaps logical block address of bad block to spare sectors • Each disk is extensively tested during

The memory hierarchy Level 1 2 3 4 Device Fastest registers (2 GHz CPU) Main memory Secondary storage (disk) Mass storage (CD-ROM library) Access Time 0. 5 ns 10 -70 ns 7 ms a few s