Способы сортировки массива Перегруппирование заданного множества объектов

Способы сортировки массива

Перегруппирование заданного множества объектов в определенном порядке называют сортировкой. Почему сортировке уделяется большое внимание? Вы это поймете, прочитав цитаты двух великих людей. "Даже если бы сортировка была почти бесполезна, нашлась бы масса причин заняться ею! Изобретательные методы сортировки говорят о том, что она и сама по себе интересна как объект исследования. " /Д. Кнут/ "Создается впечатление, что можно построить целый курс программирования, выбирая примеры только из задач сортировки. " /Н. Вирт/

Отличительной особенностью сортировки является то обстоятельство, что эффективность алгоритмов, реализующих ее, прямо пропорциональна сложности понимания этого алгоритма. Другими словами, чем легче для понимания метод сортировки массива, тем ниже его эффективность.

Задача. Даны две целочисленные переменные х и y. Составить фрагмент программы, после выполнения которого значения этих переменных распределяются в порядке убывания. Обмен значений переменных нужно производить лишь в том случае, если х < у. Для того чтобы не потерять начальное значение переменной х, введем дополнительную переменную t. if x < y then begin t : = x; x : = y; y : = t; end;

Задача. Составить фрагмент программы поиска максимального числа из трех введенных с клавиатуры чисел. Пусть а, b, c – вводимые с клавиатуры числа, max – максимальное из их значений. На первом шаге предположим , что а – максимальное из чисел и поэтому max : = a. Затем сравним значение предполагаемого максимума со значениями переменных b и с. Если значение max окажется меньше, чем значение очередной переменной, то переопределим значение максимума. … mах : = a; if mах < b then mах : = b; if mах < c then mах : = c; …

Задача. Дан массив а, состоящий из 10 элементов. Составить программу поиска максимального элемента массива. Используем идею предыдущей задачи. Перед началом поиска выберем условно в качестве максимального первый элемент массива max : = a[1]. Затем по очереди каждый элемент массива сравним со значением переменной m. Если он окажется больше, то изменим значение max. После анализа всех элементов массива переменная max содержит значение максимального элемента массива. … max : = a[1]; for i : = 2 to 10 do if max < a[i] then max : = a[i]; …

Виды сортировок

При решении задачи сортировки обычно выдвигается требование минимального использования дополнительной памяти, из которого вытекает недопустимость применения дополнительных массивов. Для оценки быстродействия алгоритмов различных методов сортировки, как правило, используют два показателя: - количество присваиваний; - количество сравнений.

Все методы сортировки можно разделить на две большие группы: - прямые методы сортировки; - улучшенные методы сортировки. Прямые методы сортировки: 1) сортировка вставкой (включением); 2) сортировка выбором (выделением); 3) сортировка обменом ( «пузырьковая» сортировка); 4) сортировка подсчетом. Улучшенные методы сортировки основываются на тех же принципах, что и прямые, но используют некоторые оригинальные идеи для ускорения процесса

Сортировка вставкой Принцип метода заключается в следующем: массив разделяется на две части: отсортированную и не отсортированную. Элементы из не отсортированной части поочередно выбираются и вставляются в отсортированную часть так, чтобы не нарушить в ней упорядоченность элементов. • В начале работы алгоритма в качестве отсортированной части массива принимают только первый элемент, а в качестве не отсортированной – все остальные элементы. •

Таким образом, алгоритм будет состоять из (n-1)-го прохода (n – размерность массива), каждый из которых будет включать четыре действия: • взятие очередного i-го не отсортированного элемента и сохранение его в дополнительной переменной; • поиск позиции j в отсортированной части массива, в которой присутствие взятого элемента не нарушит упорядоченности элементов; • сдвиг элементов массива от i-го до j-1 -го вправо, чтобы освободить найденную позицию вставки; • вставка взятого элемента в найденную j-ю позицию.

for i : = 2 to n do begin e : = a[i]; j : = 1; while e > a[j] do inc(j); for g : = i downto j+1 do a[g] : = a[g-1]; a[j] : = e; end;

Алгоритм можно немного улучшить, соединив в одном цикле поиск позиции со сдвигом элементов массива: for i : = 2 to N do begin e : = a[i]; j : = i - 1; while (j > 0) and (e < begin a[j + 1] : = a[j]; j : = j - 1; end; a[j+1] : = e end; a[j]) do

Сортировка выбором Принцип метода: Находим (выбираем) в массиве элемент с минимальным значением на интервале от 1 -го элемента до n-го (последнего) элемента и меняем его местами с первым элементом. На втором шаге находим элемент с минимальным значением на интервале от 2 -го до n-го элемента и меняем его местами со вторым элементом. И так далее для всех элементов до n-1 -го.

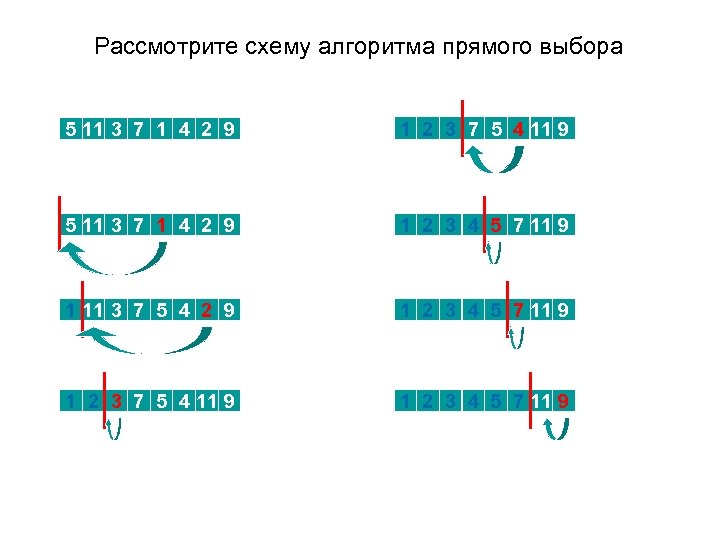
Рассмотрите схему алгоритма прямого выбора 5 11 3 7 1 4 2 9 1 2 3 7 5 4 11 9 5 11 3 7 1 4 2 9 1 2 3 4 5 7 11 9 1 11 3 7 5 4 2 9 1 2 3 4 5 7 11 9 1 2 3 7 5 4 11 9 1 2 3 4 5 7 11 9

for i : = 1 to n-1 do begin min : = a[i]; imin : = i; for j : = i + 1 to n do if a[j] < min then begin min : = a[j]; imin : = j; end; a[imin] : = a[i]; a[i] : = min; end;

Сортировка методом обмена Принцип метода: Слева направо поочередно сравниваются два соседних элемента, и, если их взаимное расположение не соответствует заданному условию упорядоченности, то они меняются местами. Далее берутся два следующих соседних элемента и так далее до конца массива. После одного такого прохода на последней n-ой позиции массива будет стоять максимальный (или минимальный) элемент ("всплыл" первый "пузырек"). Поскольку максимальный (или минимальный) элемент уже стоит на своей последней позиции, то второй проход обменов выполняется до (n-1)-го элемента. И так далее. Всего требуется (n-1) проход.

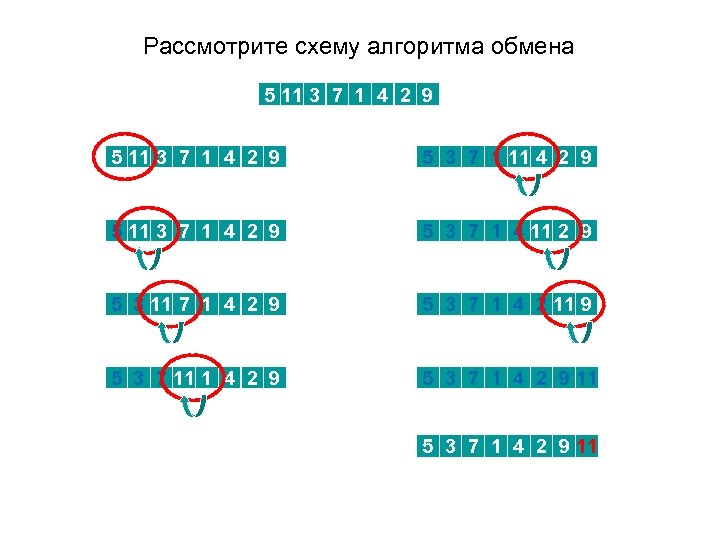
Рассмотрите схему алгоритма обмена 5 11 3 7 1 4 2 9 5 3 7 1 11 4 2 9 5 11 3 7 1 4 2 9 5 3 7 1 4 11 2 9 5 3 11 7 1 4 2 9 5 3 7 1 4 2 11 9 5 3 7 11 1 4 2 9 5 3 7 1 4 2 9 11

Рассмотрите схему алгоритма обмена Второй проход 5 3 7 1 4 2 9 11 3 5 1 4 7 2 9 11 3 5 7 1 4 2 9 11 3 5 1 4 2 7 9 11 3 5 1 7 4 2 9 11 3 5 1 4 2 7 9 11

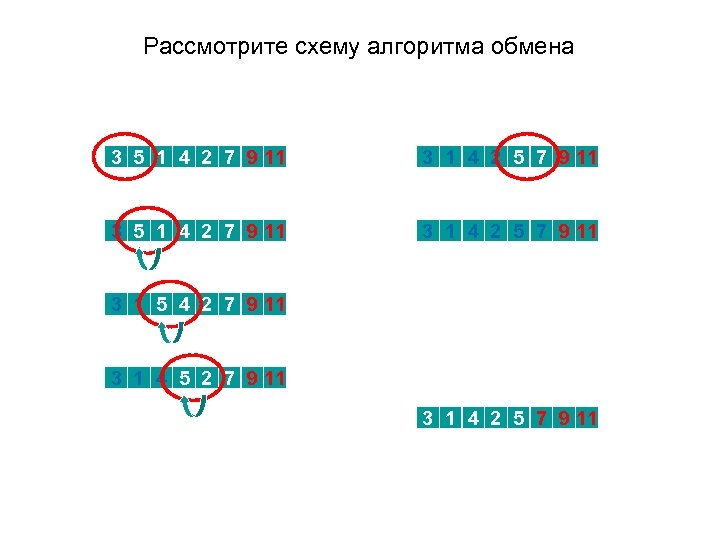
Рассмотрите схему алгоритма обмена Третий проход 3 5 1 4 2 7 9 11 3 1 4 2 5 7 9 11 3 1 5 4 2 7 9 11 3 1 4 5 2 7 9 11 3 1 4 2 5 7 9 11

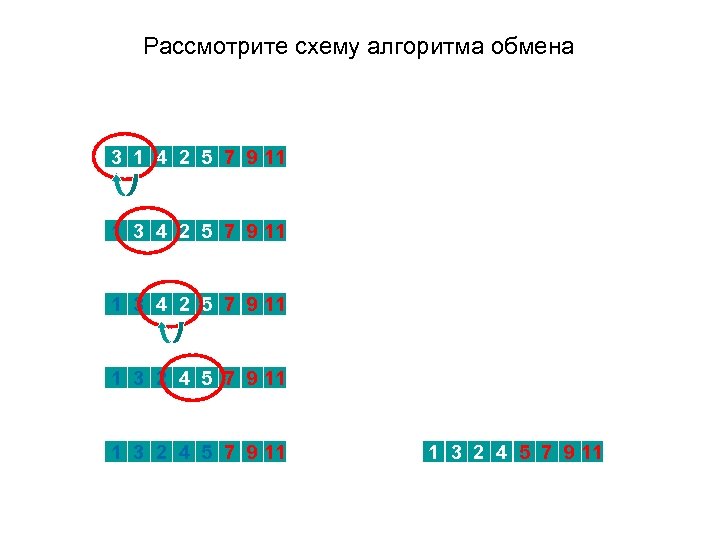
Рассмотрите схему алгоритма обмена Четвертый проход 3 1 4 2 5 7 9 11 1 3 2 4 5 7 9 11 1 3 2 4 5 7 9 11

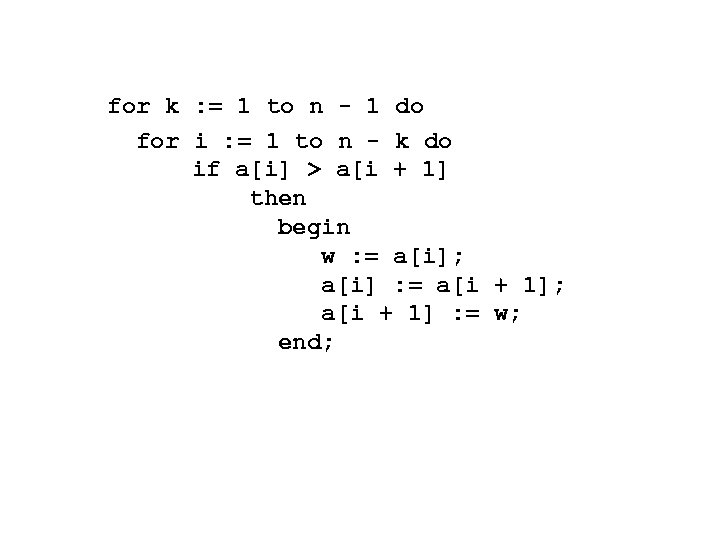
for k : = 1 to n - 1 do for i : = 1 to n - k do if a[i] > a[i + 1] then begin w : = a[i]; a[i] : = a[i + 1]; a[i + 1] : = w; end;

Сортировка подсчетом Принцип метода: Каждый элемент сравнивается со всеми остальными. Положение элемента в отсортированном массиве определяется количеством элементов меньших данного.

for i : = 1 to n do begin k : = 0; for j : = 1 to n do if a[i] > a[j] then inc(k); Sorted_a[k] : = a[i]; end; Примечания: 1. Сортировка подсчетом работает только в тех случаях, если в массиве нет одинаковых элементов. 2. Заметим, что значение счетчика k для минимального элемента останется равным 0, а для максимального элемента k будет равно n-1. Следовательно, массив Sorted_a (отсортированный массив) должен быть описан с индексами от 0 до n-1.

Программа, реализующая сортировку подсчетом: var a: array [1. . 1000] of integer; Sorted_a: array [0. . 1000] of integer; i, g, j, e, n, k: integer; begin read (n); for i: =1 to n do read (a[i]); for i : = 1 to n do begin k : = 0; for j : = 1 to n do if a[i] > a[j] then inc(k); Sorted_a[k] : = a[i]; end; for i: =0 to n-1 do write ( Sorted_a[i], ' '); end.

Быстрая сортировка массива с помощью рекурсии (быстрая сортировка) Алгоритм реализуется следующим образом: в некотором отрезке массива выбирается центральное (серединное) значение; все элементы из левой части отрезка, превосходящие центральное значение, перемещаются в правую часть, и наоборот. На следующем шаге (для которого используются рекурсивные вызовы этой же процедуры) алгоритм повторяется для обоих частей отрезка.

Рассмотрите процедуру, упорядочивающую по возрастанию значения массива A в диапазоне индексов First. . Last Procedure Quick. Sort (First, Last : integer); Var L, R, x, y : integer; Begin L : = First; R : = Last; x : = a[L+random(R–L+1)]; Repeat While a[L] < x do Inc(L); While a[R] > x do Dec(R); If L <= R Then Begin y : = a[L]; a[L] : = a[R]; a[R] : = y; Inc(L); Dec(R); End; Until L > R; If First < R Then Quick. Sort (First, R); If L < Last Then Quick. Sort (L, Last); End;

Программа, реализующая быструю сортировку: var a: array [1. . 1000] of integer; i, n: integer; Procedure Quick. Sort (First, Last : integer); {текст процедуры см. предыдущий слайд} Begin {чтение массива} read (n); for i: =1 to n do read (a[i]); {вывод неотсортированного массива} for i: =1 to n do write ( a[i], ' '); writeln; Quick. Sort (1, n); {вызов процедуры сортировки} {вывод отсортированного массива} for i: =1 to n do write ( a[i], ' '); end.

• Самостоятельное • решение задач

1. В массиве X(N) каждый элемент равен 0, 1 или 2. Переставить элементы массива так, чтобы сначала располагались все единицы, затем все двойки и, наконец, все нули (дополнительного массива не заводить). 2. В заданной последовательности все элементы, не равные нулю, расположить сохраняя их порядок следования, в начале последовательности, а нулевые элементы - в конце последовательности. Дополнительного массива не заводить. 3. Отсортировать массив по возрастанию, используя процедуру Swap, которая меняет местами 2 элемента. 4. Составьте алгоритм, упорядочивающий элементы массива, стоящие на нечетных местах, в возрастающем порядке, а на четных – в убывающем.

• 5. Из двух упорядоченных одномерных массивов (длины K и N) сформируйте одномерный массив размером K+N, упорядоченный так же, как исходные массивы. • 6. Из двух упорядоченных одномерных массивов (длины K и N) сформируйте одномерный массив размером K+N, упорядоченный в обратную сторону. • 7. Составьте алгоритм, упорядочивающий заданную последовательность чисел так, чтобы каждый элемент, стоящий на четном месте, был больше каждого из соседних. • 8. Дан упорядоченный целочисленный массив. Сформировать второй массив всех таких различных значений, которые в первом массиве встречаются по два и более раза.

• 9. Дан упорядоченный целочисленный массив. Сформировать второй массив всех таких различных чисел, которые ни разу в первом массиве не встречаются и имеют величину больше минимального и меньше максимального из чисел первого массива. • 10. Дана вещественная матрица размером 7 x 4. Переставляя ее строки и столбцы, добиться того, чтобы наибольший элемент (один из них) оказался в левом верхнем углу. • 11. В заданном целочисленном массиве найти элементы, сумма которых равна данному числу, в предположении, что такие числа существуют. • 12. Дан массив А, состоящий из n элементов. Осуществить перестановку элементов массива на M элементов вправо.