СПОСОБЫ ПРЕДСТАВЛЕНИЯ АЛГОРИТМОВ 1 Чтобы довести алгоритмы

СПОСОБЫ ПРЕДСТАВЛЕНИЯ АЛГОРИТМОВ 1

Чтобы довести алгоритмы до пользователя, они должны быть формализованы по некоторым правилам (соглашениям) посредством конкретных изобразительных средств. 2

Формы записи алгоритмов: словесная; формульно-словесная; блок-схемы; Flow-диаграммы; диаграммы Насси-Шнейдермана; программы. 3

ПРИМЕР. Разработать алгоритм Эвклида нахождения наибольшего общего делителя (НОД) двух натуральных чисел m и n. 4

Словесный способ. Предполагает запись алгоритма в произвольной форме на естественном языке. Недостатком словесного способа записи алгоритма является отсутствие более или менее строгой формализации и наглядности алгоритма. 5

Формульно-словесный способ. Основан на задании инструкций о выполнении действий с использованием математических символов и выражений в сочетании с пояснениями на естественном языке. 6

Поиск НОД(m, n). 1) Ввод m и n. 2) Если m n, перейти к шагу 3, иначе – к шагу 4. 3) Если m>n, то m: = m - n, иначе n: = n – m; перейти к шагу 2. 4) Вывод результатов (значения n). Конец. 7

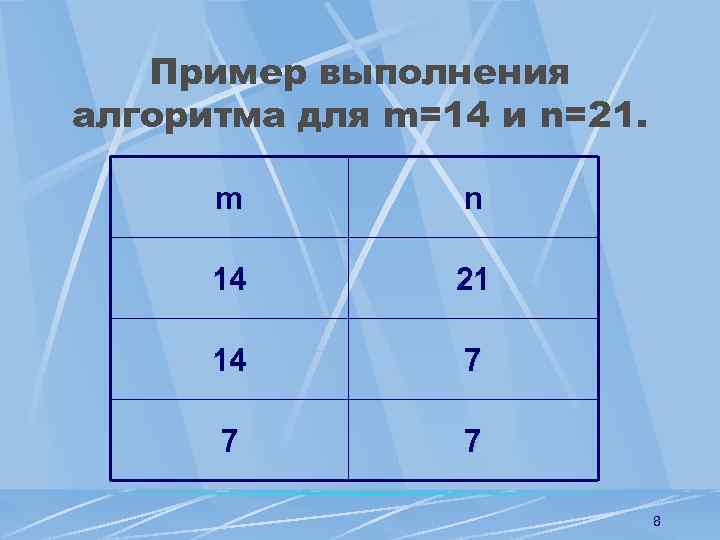
Пример выполнения алгоритма для m=14 и n=21. m n 14 21 14 7 7 7 8

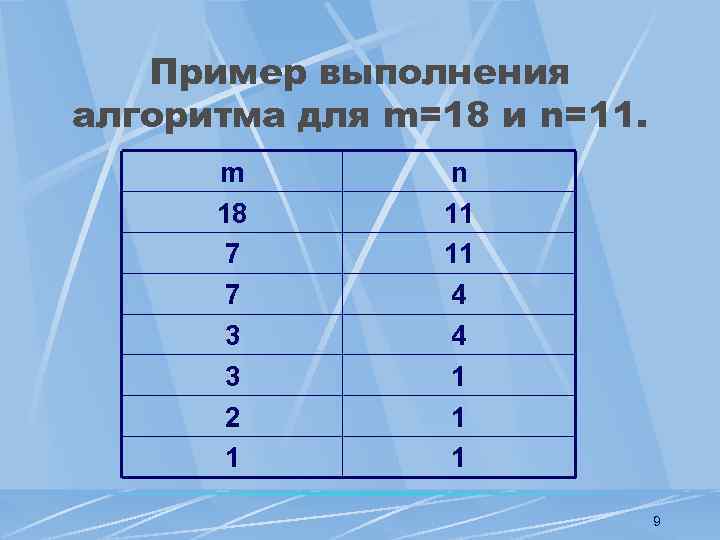
Пример выполнения алгоритма для m=18 и n=11. m 18 7 7 3 3 2 1 n 11 11 4 4 1 1 1 9

Формульно-словесный способ более компактен и нагляден по сравнению со словесным способом. Он общепринят при описании различного рода математических выкладок, доказательств теорем, легко читается и понятен без специальной подготовки. 10

Блок-схемы алгоритмов. Блок-схемой алгоритма называется графическое изображение логической структуры алгоритма, в которой каждый этап процесса переработки данных представляется в виде геометрических фигур (блоков), имеющих определенную конфигурацию в зависимости от характера выполняемых операций. 11

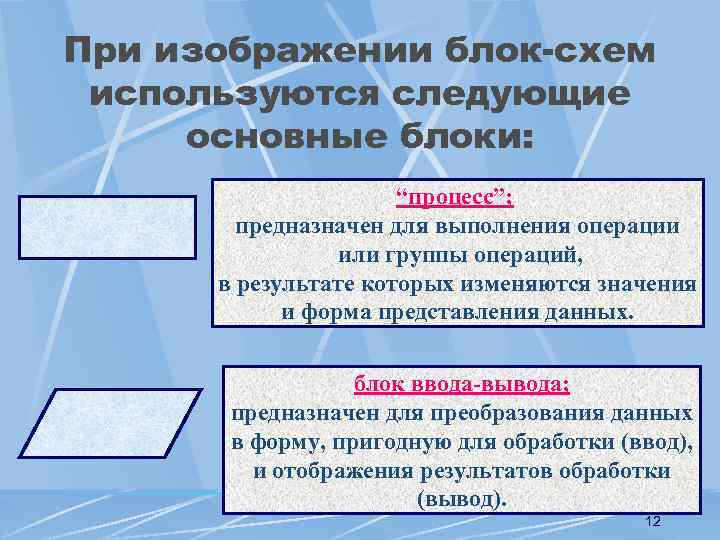
При изображении блок-схем используются следующие основные блоки: “процесс”; предназначен для выполнения операции или группы операций, в результате которых изменяются значения и форма представления данных. блок ввода-вывода; предназначен для преобразования данных в форму, пригодную для обработки (ввод), и отображения результатов обработки (вывод). 12

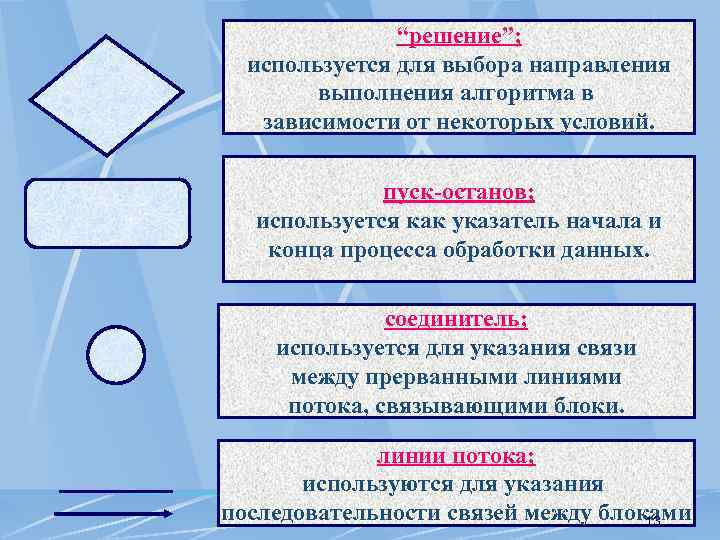
“решение”; используется для выбора направления выполнения алгоритма в зависимости от некоторых условий. пуск-останов; используется как указатель начала и конца процесса обработки данных. соединитель; используется для указания связи между прерванными линиями потока, связывающими блоки. линии потока; используются для указания последовательности связей между блоками 13

Замечание. Каждый блок имеет строго определенные размеры, определяемые соответствующим ГОСТом. 14

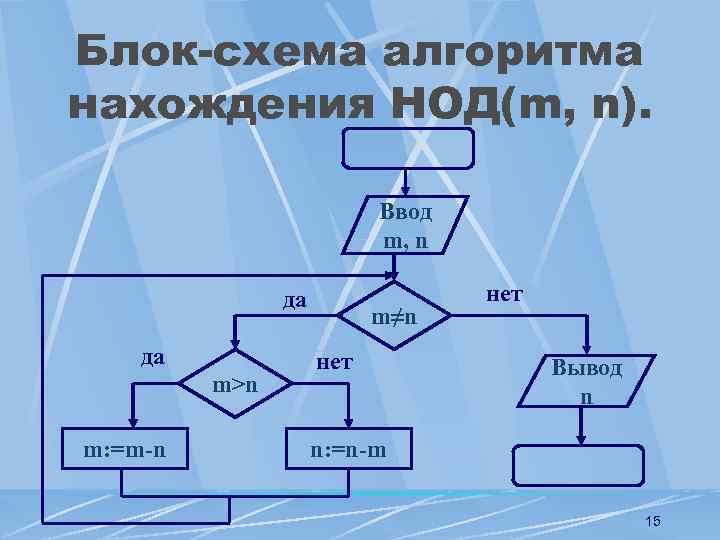
Блок-схема алгоритма нахождения НОД(m, n). Ввод m, n да да m>n m: =m-n m≠n нет Вывод n n: =n-m 15

FLOW-диаграммы. Относятся к визуальным средствам описания алгоритмов. При использовании FLOW-диаграмм каждое действие оформляется в виде прямоугольника и помечается на естественном языке или с использованием языка математики. 16

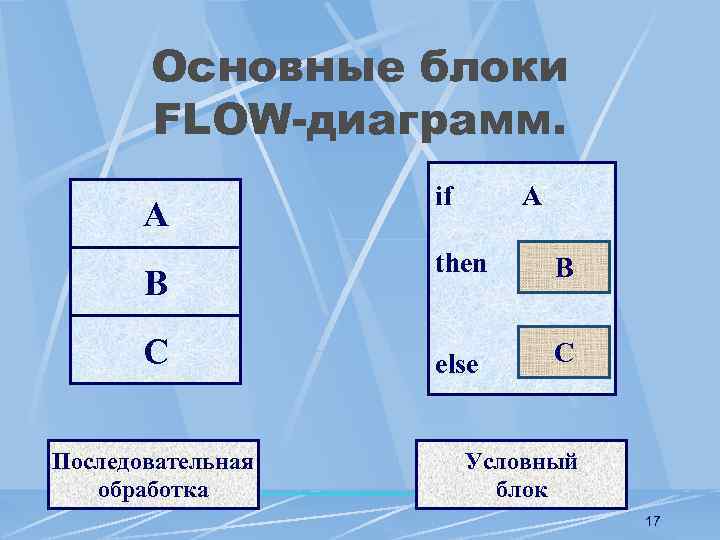
Основные блоки FLOW-диаграмм. А B C Последовательная обработка if A then B else C Условный блок 17

Блоки циклов. While do A B Do B For until A do A B 18

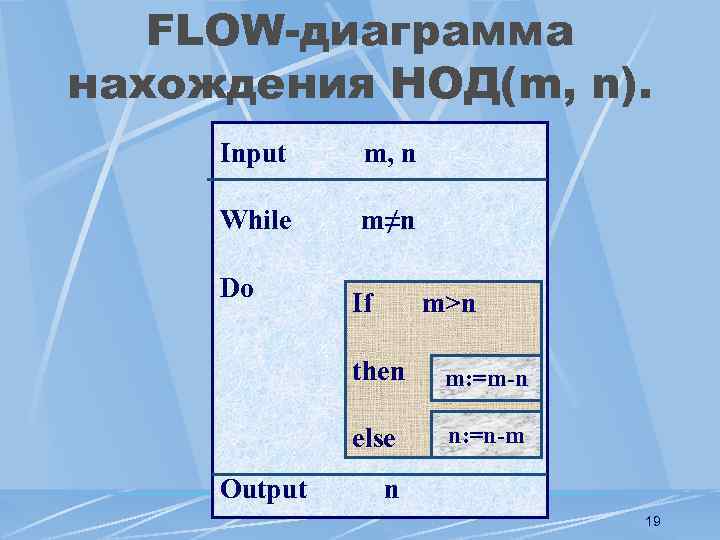
FLOW-диаграмма нахождения НОД(m, n). Input m, n While m≠n Do If m>n then else Output m: =m-n n: =n-m n 19

Диаграммы Насси. Шнейдермана. Дальнейшее развитие FLOWдиаграмм получили диаграммы Насси-Шнейдермана. На этих диаграммах блоки последовательностей обработки и циклов изображаются так же, как и соответствующие блоки FLOWдиаграмм. 20

Условный же блок имеет вид: Условие А Да В Нет С 21

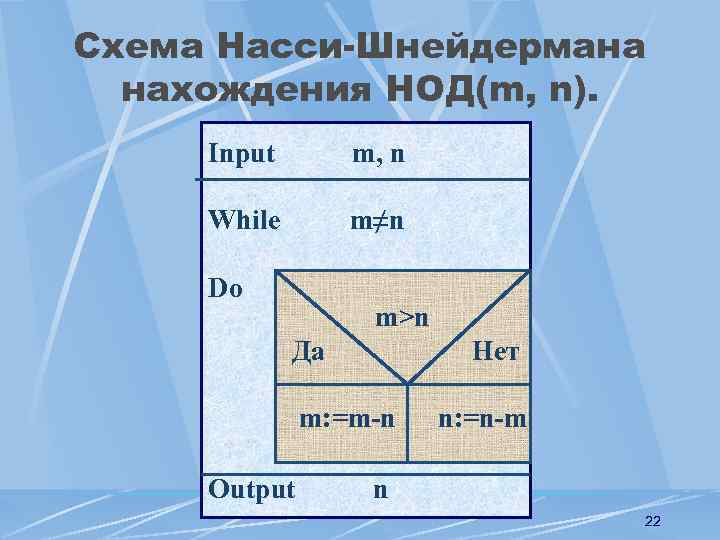
Схема Насси-Шнейдермана нахождения НОД(m, n). Input m, n While m≠n Do m>n Да Нет m: =m-n Output n: =n-m n 22

Программы. Представление алгоритма на языке программирования – конечная цель программирования. При записи алгоритмов в виде программ учитываются строгие правила и особенности построения конструкций языка, допустимый набор функций и др. 23

Программа нахождения НОД(m, n) на языке Паскаль. program nod; var m, n: word; begin Read(m, n); While m<>n do if m>n then m: =m-n else n: =n-m; Write(‘nod= ‘, n) end. 24

Упражнения. Описать с помощью любых средств алгоритмы решения следующих задач. 1. Для заданных действительных чисел а и b решить линейное уравнение: ах + b = 0 25

Упражнения. 2. Для заданных действительных чисел а, b и с вычислить значение выражения: ||a–b|–c| 26

Упражнения. 3. Даны три действительных числа: а, b и с. Пусть третье число с – это код операции между первыми двумя: 1 – ‘+’, 2 – ‘-’, 3 – ‘*’. Вывести результат операции. 27

Примеры блок-схем алгоритмов. Пример 1. Определить, сколько цифр в заданном натуральном числе n. 28

Ввод n i: =1 n: =[n/10] Да n=0 Вывод i Нет i: =i+1 29

УПРАЖНЕНИЕ Задано натуральное число N. Изменить в нем порядок цифр на обратный. 327 723 30

Примеры блок-схем алгоритмов. Пример 2. Разработать алгоритм, проверяющий, является ли заданное натуральное число n простым. Замечание. Число является простым, если оно делится лишь простым само на себя и на единицу. 31

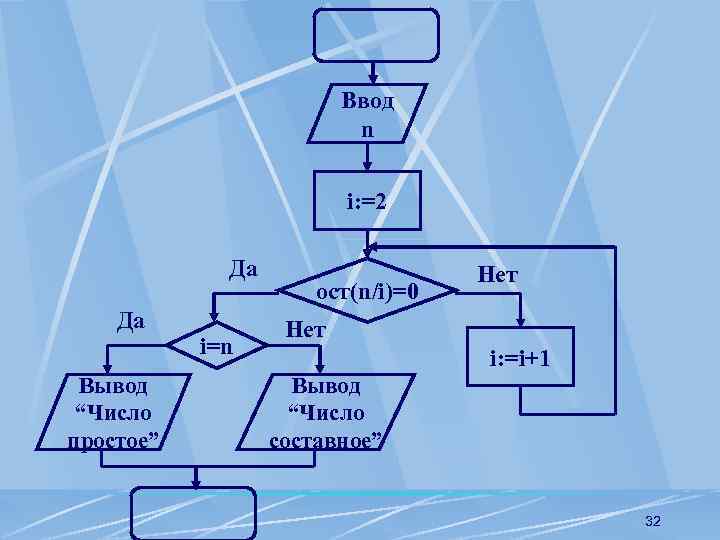
Ввод n i: =2 Да Да Вывод “Число простое” i=n ост(n/i)=0 Нет i: =i+1 Вывод “Число составное” 32

Примеры блок-схем алгоритмов. Пример 3. Алгоритм сортировки массива целых чисел по методу “пузырька”. Задача сортировки сводится к следующему: Пусть заданы целые числа в виде элементов массива а 1, а 2, …, аn. Требуется расположить их в порядке возрастания. 33

Метод “пузырька” основывается на следующем алгоритме: 1) массив просматривается с конца к началу; 2) сравниваются пары соседних элементов. Если они не удовлетворяют требуемому условию, то они меняются местами; если удовлетворяют, то остаются на своих местах; 3) процесс просмотра, сравнения и обмена повторяется до тех пор, пока не будут упорядочены все элементы. 34

Пример. Пусть задан массив из 8 элементов (n=8): 44 55 12 42 94 18 6 67 Необходимо отсортировать его в порядке возрастания. 35

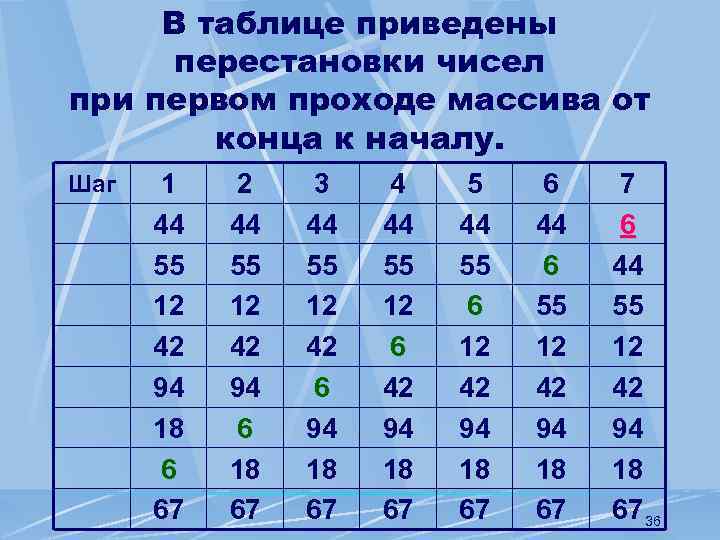
В таблице приведены перестановки чисел при первом проходе массива от конца к началу. Шаг 1 44 55 12 42 94 18 6 67 2 44 55 12 42 94 6 18 67 3 44 55 12 42 6 94 18 67 4 44 55 12 6 42 94 18 67 5 44 55 6 12 42 94 18 67 6 44 6 55 12 42 94 18 67 7 6 44 55 12 42 94 18 67 36

В результате перестановок самый “легкий” элемент со значением 6 “всплыл” на “поверхность”, то есть занял положение в соответствии со своим весом – первую позицию в массиве. Теперь его можно исключить из дальнейшего анализа. 37

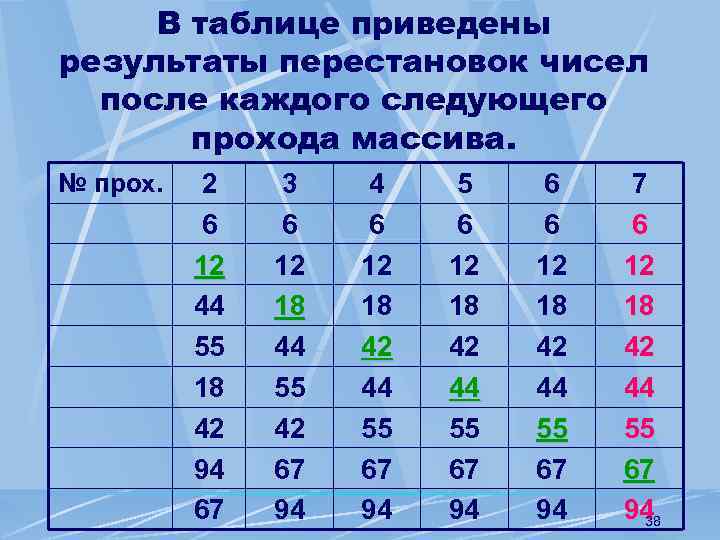
В таблице приведены результаты перестановок чисел после каждого следующего прохода массива. № прох. 2 6 12 44 55 18 42 94 67 3 6 12 18 44 55 42 67 94 4 6 12 18 42 44 55 67 94 5 6 12 18 42 44 55 67 94 6 6 12 18 42 44 55 67 94 7 6 12 18 42 44 55 67 94 38

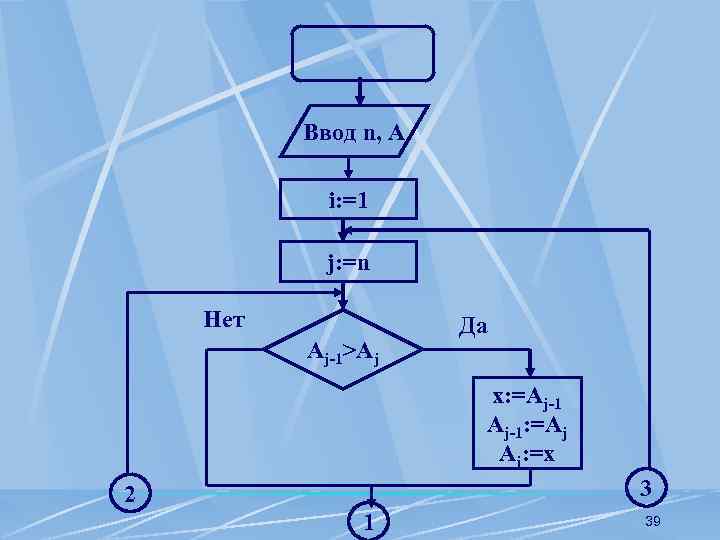
Ввод n, A i: =1 j: =n Нет Aj-1>Aj Да x: =Aj-1: =Aj Aj: =x 3 2 1 39

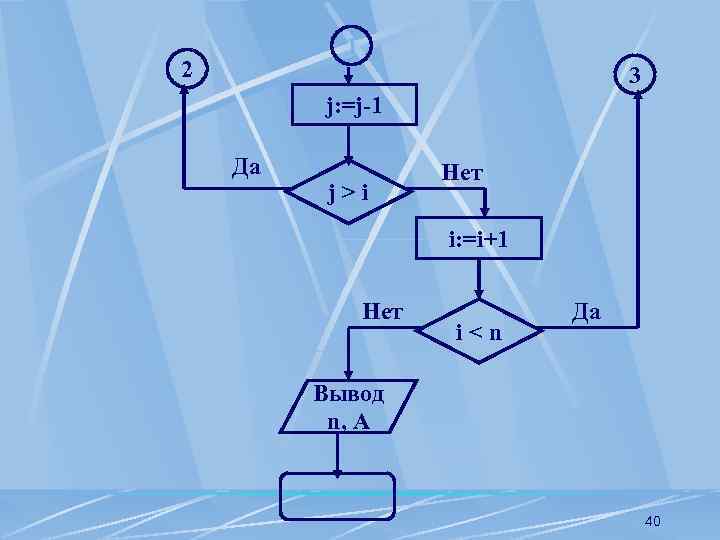
1 2 3 j: =j-1 Да j>i Нет i: =i+1 Нет i<n Да Вывод n, A 40

УПРАЖНЕНИЕ (необязательное) Усовершенствовать алгоритм метода “пузырька”, определяя ситуацию, когда на некотором шаге все элементы массива уже упорядочены. Замечание. Можно использовать Замечание вспомогательную переменную “флажок”, которая принимает 2 значения 1 или 0, в зависимости от того, были или не были обмены соседних элементов на определенном шаге просмотра массива. 41