СПОСОБЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ 1. Способ архитекторов. В основу этого способа положено свойство перспективных проекций параллельных прямых, которое заключается в том, что они сходятся в одной точке (имеют общую точку схода F). 2. Радиальный способ заключается в том, что перспектива любой точки определяется как след луча зрения (т. е. как точка пересечения луча зрения, проходящего через заданную точку, с картинной плоскостью). Способ разработан немецким художником, математиком и гравером Альбертом Дюрером (1471 − 1528) и поэтому иногда называется способом Дюрера. 3. Способ сетки. Способ построения перспективы с помощью сетки заключается в том, что предварительно на ортогональных проекциях наносят равномерную ортогональную сетку, а затем строят перспективное изображение этой сетки.
ПОСТРОЕНИЕ ПЕРСПЕКТИВЫ ОБЪЕКТА СПОСОБОМ АРХИТЕКТОРОВ В практике построения перспектив наибольшее распространение получил способ архитекторов. Этот способ применяется при построении перспективных изображений различных сооружений, которые в плане имеют два доминирующих направления линий (например, здания, мосты, путепроводы). Использование двух точек схода перспектив параллельных горизонтальных прямых объекта доминирующих направлений обеспечивает большую графическую точность и простоту построения перспективного изображения.
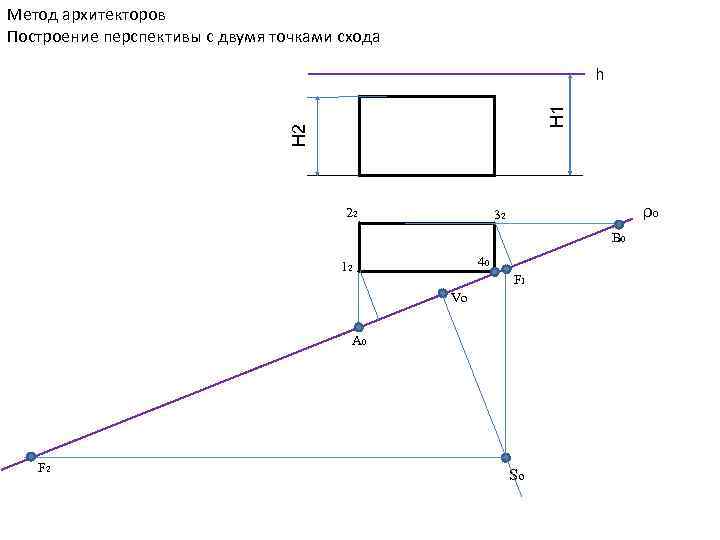
Метод архитекторов Построение перспективы с двумя точками схода Н 2 Н 1 h 22 ρо 32 В 0 40 12 F 1 Vo A 0 F 2 Sо
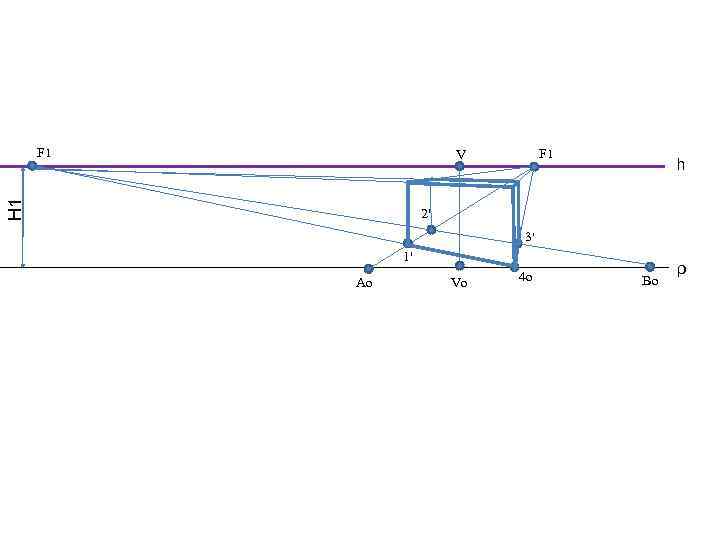
F 1 Н 1 V h 2' 3' 1' Ao Vo 4 o Bo ρ
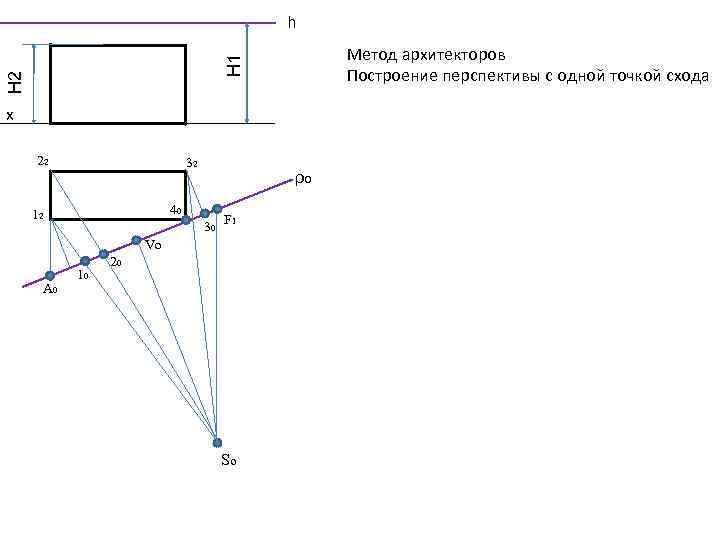
h Н 2 Н 1 Метод архитекторов Построение перспективы с одной точкой схода x 22 32 40 12 ρо 30 F 1 Vo A 0 10 20 Sо
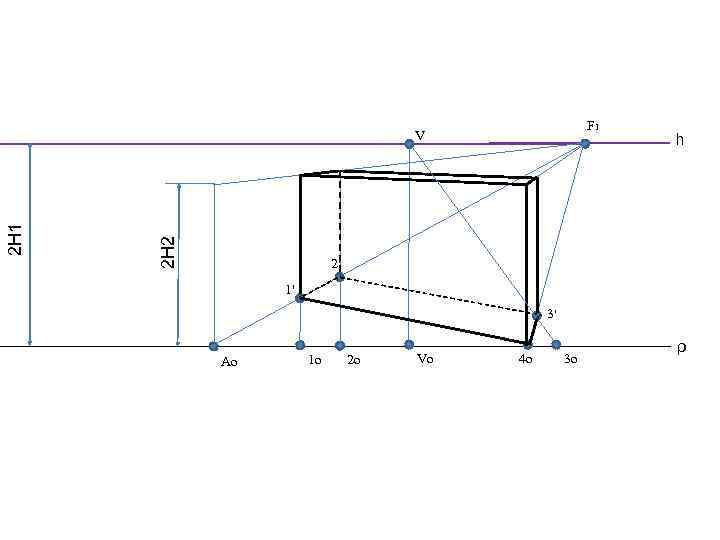
F 1 2 Н 2 2 Н 1 V h 2' 1' 3' Ao 1 o 2 o Vo 4 o 3 o ρ
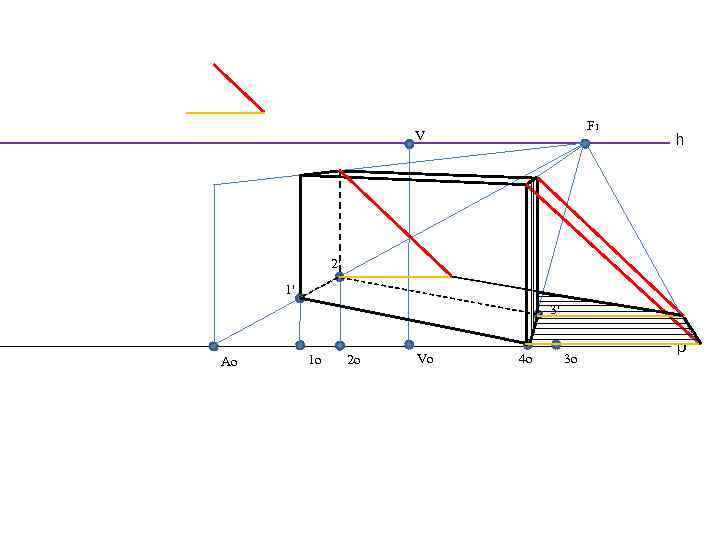
F 1 V h 2' 1' 3' Ao 1 o 2 o Vo 4 o 3 o ρ
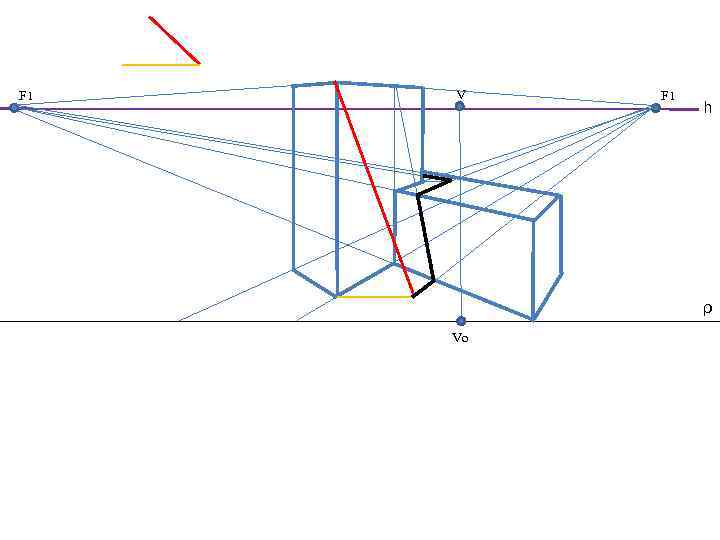
F 1 V F 1 h ρ Vo
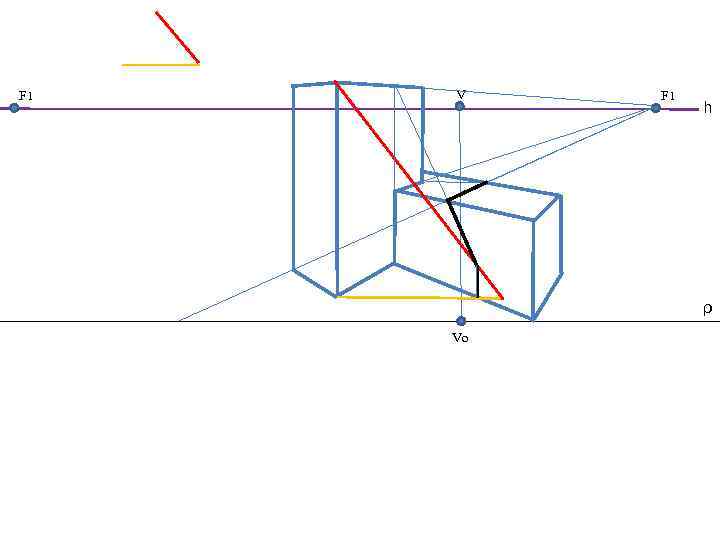
F 1 V F 1 h ρ Vo
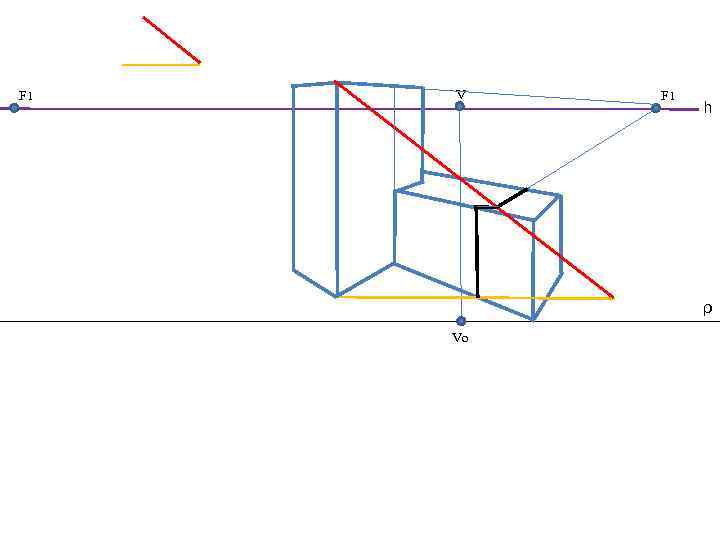
F 1 V F 1 h ρ Vo
Перспектива. метод сетки Перспектива сетки квадратов Пусть заданы аппарат проецирования и сетка квадратов, стороны которых параллельны и перпендикулярны плоскости картины и примыкают к ней. 1. Проводят основание картины I ~ t И линию горизонта h -h, на которой отмечают главную точку V, дистанционные точки D 1 и D 2. Точки D 1 и D 2 находятся от точки V на расстоянии равном расстоянию от точки зрения. 2. На основании картины откладываются последовательно отрезки, равные стороне квадрата. 3. Соединив точки, нанесенные на основании с точкой V получим перспективное изображение связки прямых, перпендикулярных картине. 4. Крайние точки соединяют с точками дальности и отмечают точки пересечения перспектив диагоналей с ранее построенными прямыми. 5. Через отмеченные точки проводят прямые, параллельные t-t Перспективную сетку квадратов можно рассматривать как своеобразную систему перспективных масштабов, с помощью которых производят измерения на картине: масштабы широты на линии t-t масштабы глубины на прямых 1 КР или 50 Р - перспективы равных отрезков, (рис. )
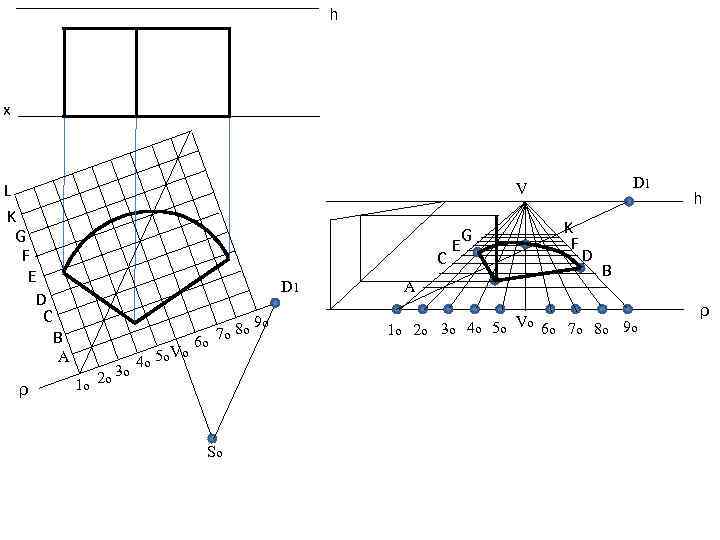
h x L K G F E D C C D 1 B A ρ D 1 V 3 о 1 о 2 о 4 о 5 о Vо 9 о 7 о 8 о 6 о Sо A E G K F D h B Vо 6 о 7 о 8 о 9 о 1 о 2 о 3 о 4 о 5 о ρ
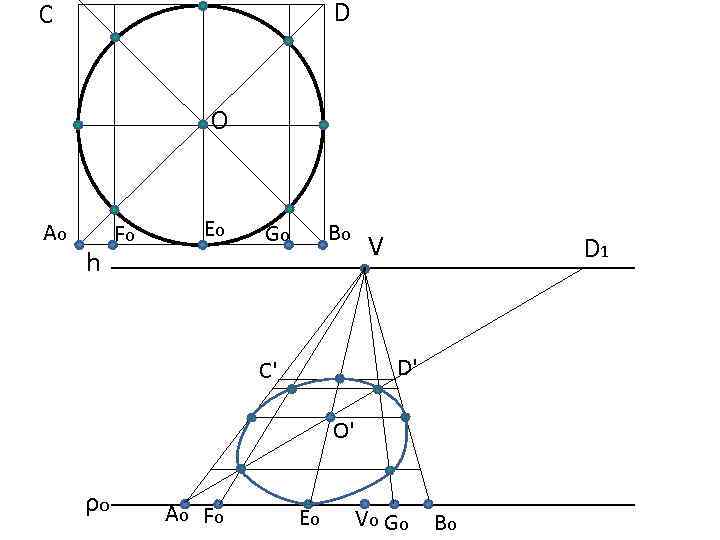
D C О Аo h Fo Eo Bo Go V D 1 D' C' O' ρo Аo Fo Eo Vo G o Bo
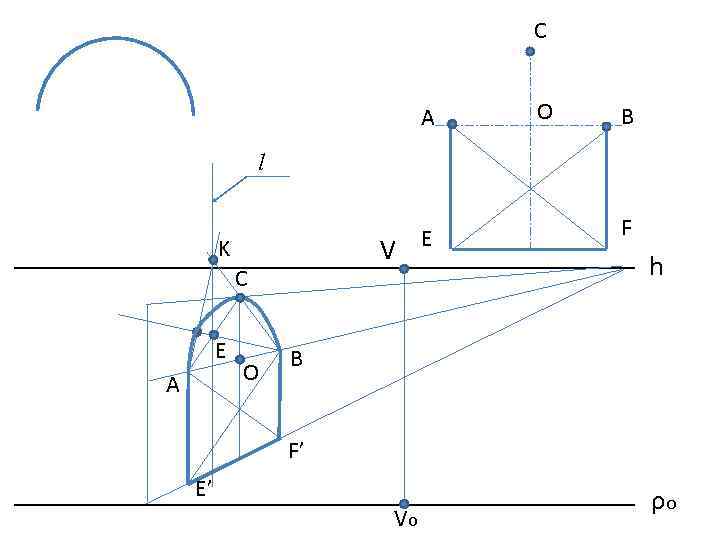
C A O B l V K C E A O E F h B F’ E’ Vo ρo
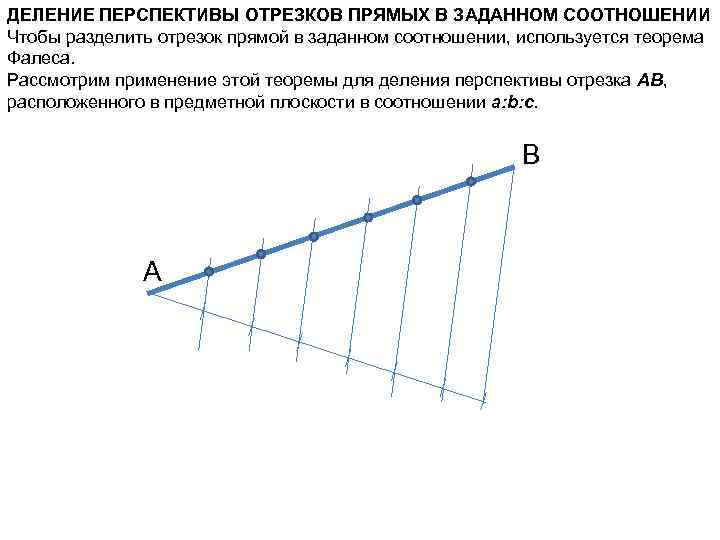
ДЕЛЕНИЕ ПЕРСПЕКТИВЫ ОТРЕЗКОВ ПРЯМЫХ В ЗАДАННОМ СООТНОШЕНИИ Чтобы разделить отрезок прямой в заданном соотношении, используется теорема Фалеса. Рассмотрим применение этой теоремы для деления перспективы отрезка АВ, расположенного в предметной плоскости в соотношении а: b: с. B A
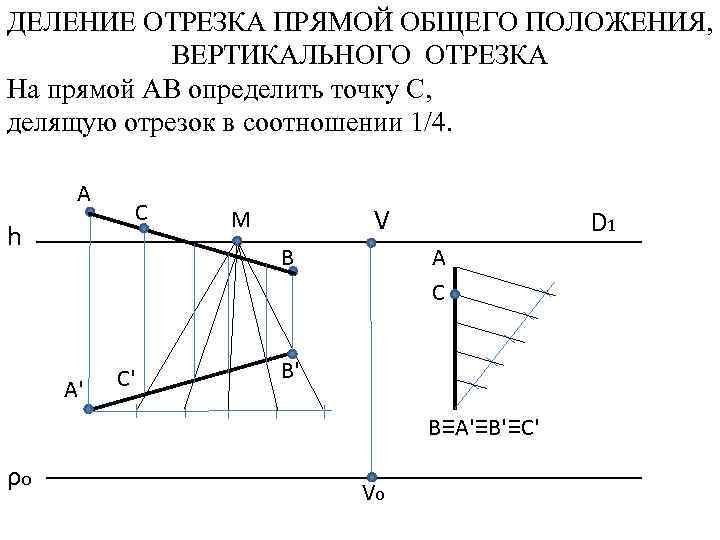
ДЕЛЕНИЕ ОТРЕЗКА ПРЯМОЙ ОБЩЕГО ПОЛОЖЕНИЯ, ВЕРТИКАЛЬНОГО ОТРЕЗКА На прямой АВ определить точку С, делящую отрезок в соотношении 1/4. A h C V M B A' C' D 1 A C B' B≡A'≡B'≡C' ρo Vo
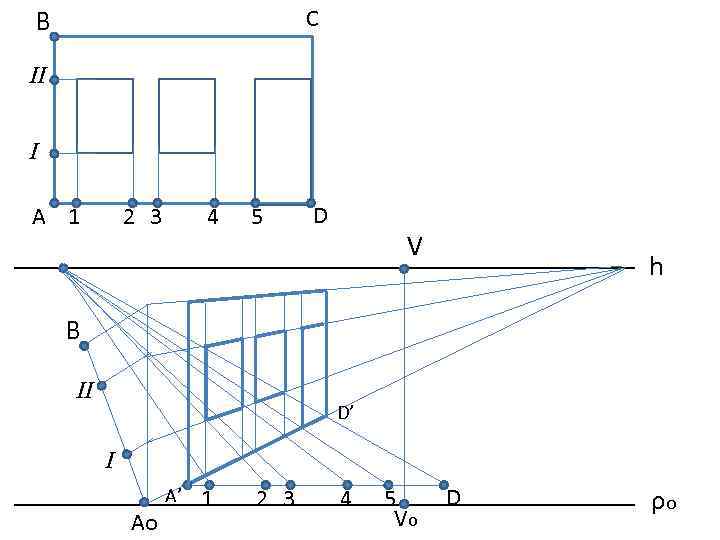
B C II I A 1 2 3 4 5 D V h B II D’ I Ao A’ 1 2 3 4 5 Vo D ρo
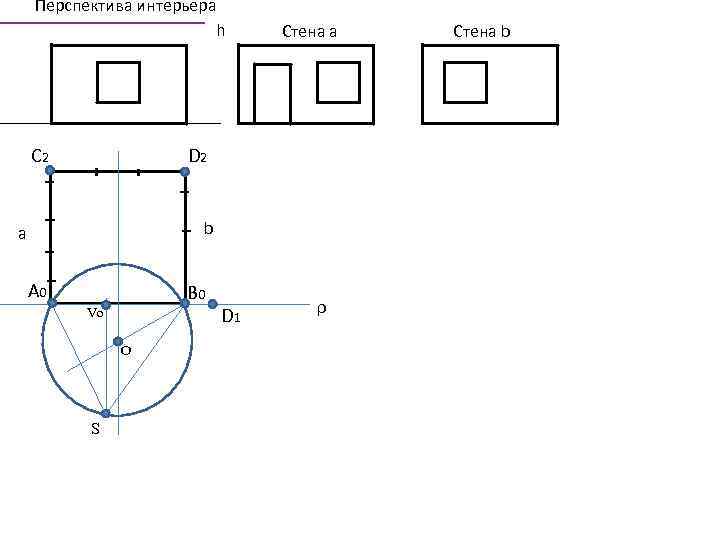
Перспектива интерьера h C 2 Стена а D 2 b а A 0 B 0 Vo O S D 1 ρ Стена b
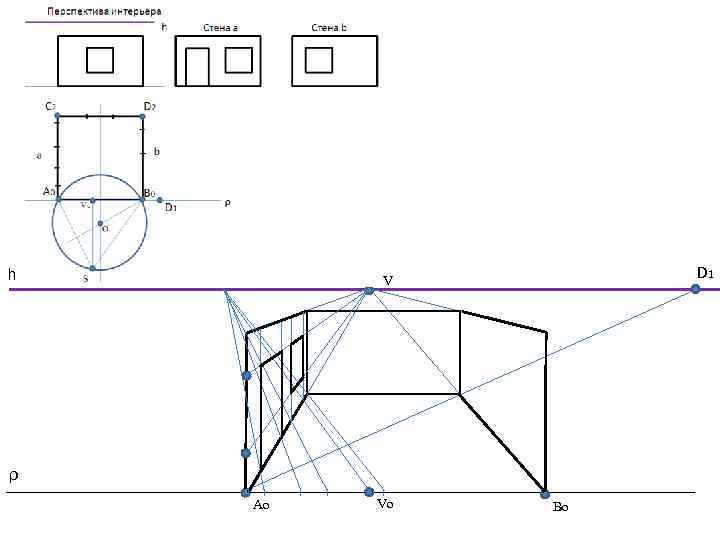
h D 1 V ρ Аo Vo Вo
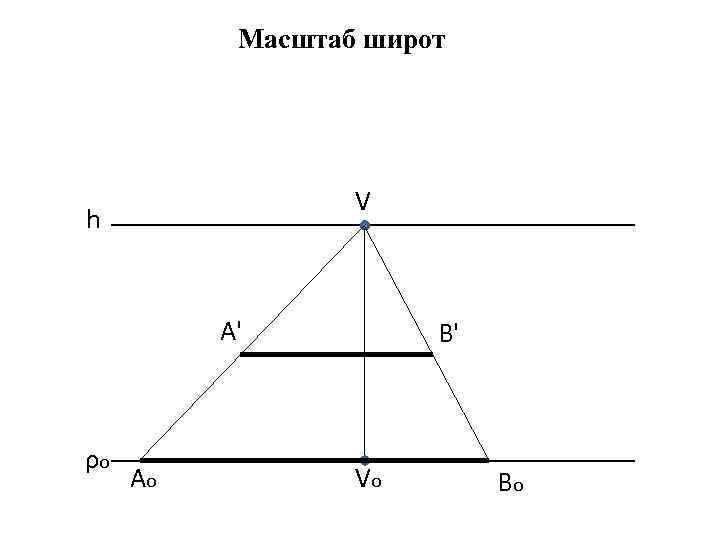
Масштаб широт V h A' ρo Аo B' Vo Bo
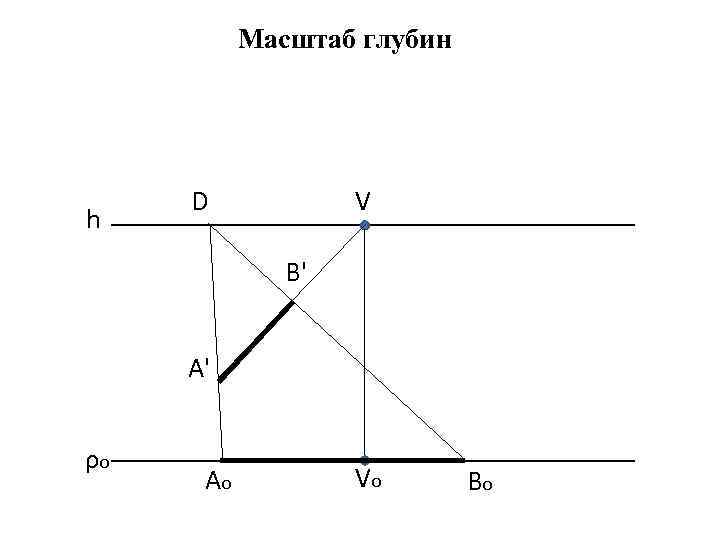
Масштаб глубин h D V B' A' ρo Аo Vo Bo
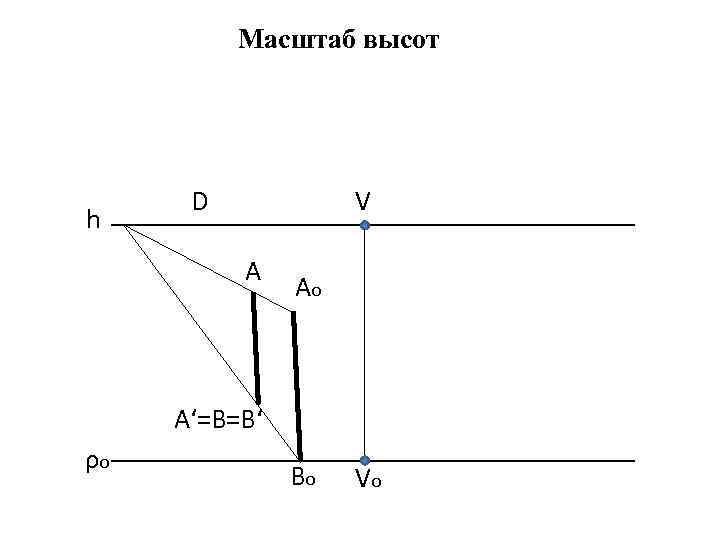
Масштаб высот h D V А Аo A‘=В=В‘ ρo Bo Vo
Скачать презентацию СПОСОБЫ ПОСТРОЕНИЯ ПЕРСПЕКТИВЫ ГЕОМЕТРИЧЕСКИХ ОБЪЕКТОВ 1 Способ архитекторов
способы построения перспективы.ppt