Splatting.ppt
- Количество слайдов: 80
 Splatting Jian Huang, CS 594, Spring 2002 This set of slides reference slides made by Ohio State University alumuni over the past several years.
Splatting Jian Huang, CS 594, Spring 2002 This set of slides reference slides made by Ohio State University alumuni over the past several years.
 Volumetric Ray Integration color opacity 1. 0 object (color, opacity)
Volumetric Ray Integration color opacity 1. 0 object (color, opacity)
 Splatting • • • Lee Westover - Vis 1989; SIGGRAPH 1990 Object order method Front-To-Back or Back-To-Front Original method - fast, poor quality Many many improvements since then! – – – Crawfis’ 93: textured splats Swan’ 96, Mueller’ 97: anti-aliasing Mueller’ 98: image-aligned sheet-based splatting Mueller’ 99: post-classified splatting Huang’ 00: new splat primitive: Fast. Splats
Splatting • • • Lee Westover - Vis 1989; SIGGRAPH 1990 Object order method Front-To-Back or Back-To-Front Original method - fast, poor quality Many many improvements since then! – – – Crawfis’ 93: textured splats Swan’ 96, Mueller’ 97: anti-aliasing Mueller’ 98: image-aligned sheet-based splatting Mueller’ 99: post-classified splatting Huang’ 00: new splat primitive: Fast. Splats
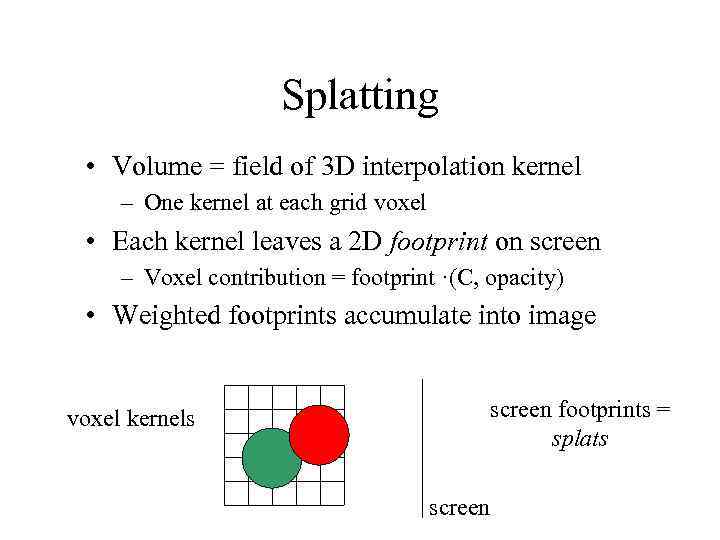 Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
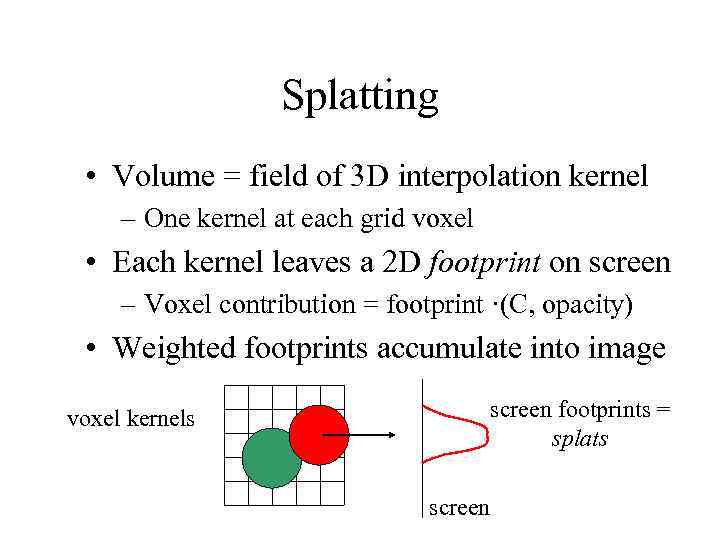 Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
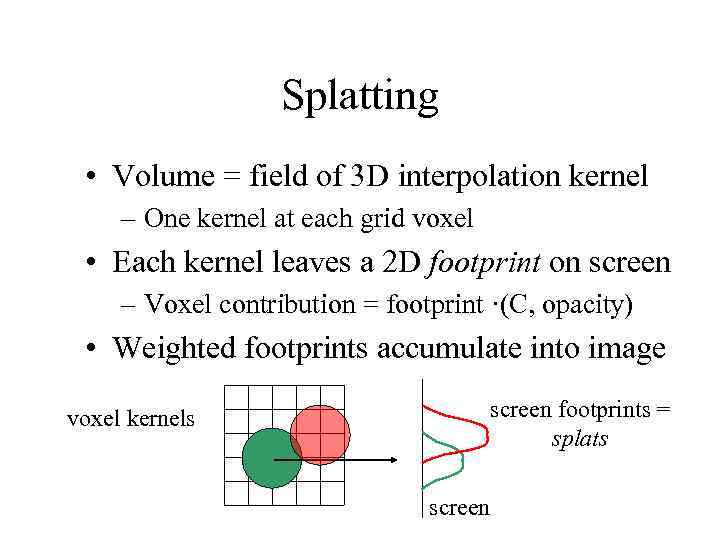 Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
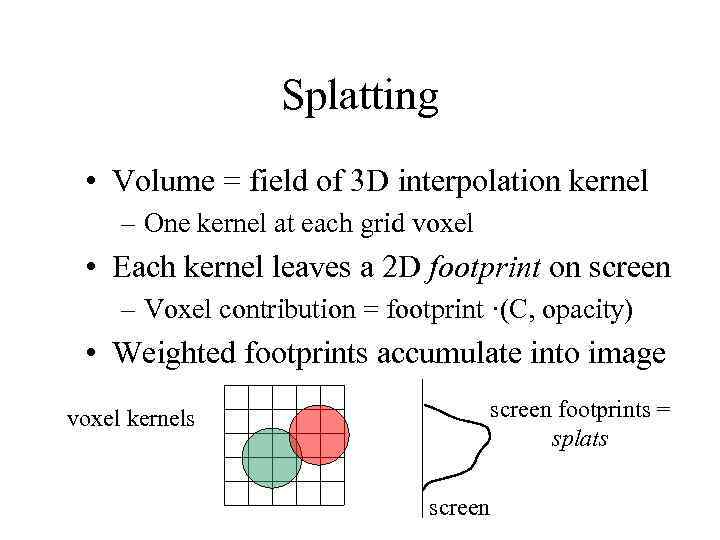 Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
Splatting • Volume = field of 3 D interpolation kernel – One kernel at each grid voxel • Each kernel leaves a 2 D footprint on screen – Voxel contribution = footprint ·(C, opacity) • Weighted footprints accumulate into image voxel kernels screen footprints = splats screen
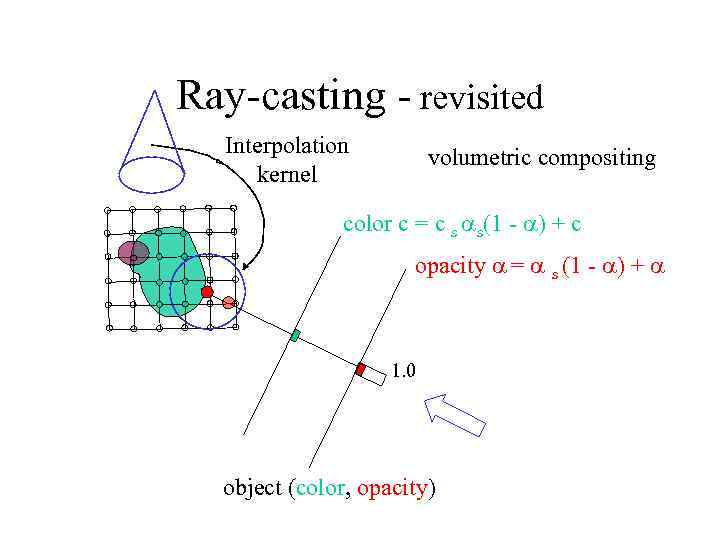 Ray-casting - revisited Interpolation kernel volumetric compositing color c = c s s(1 - ) + c opacity = s (1 - ) + 1. 0 object (color, opacity)
Ray-casting - revisited Interpolation kernel volumetric compositing color c = c s s(1 - ) + c opacity = s (1 - ) + 1. 0 object (color, opacity)
 Ray-casting - revisited • (ideally) we would reconstruct the continuous volume (cloud) using the interpolation kernel h: • the we would compute the analytic integral along a ray r: (hey! Which optical model is this equation? ? ) • this can only be approximated by discretization
Ray-casting - revisited • (ideally) we would reconstruct the continuous volume (cloud) using the interpolation kernel h: • the we would compute the analytic integral along a ray r: (hey! Which optical model is this equation? ? ) • this can only be approximated by discretization
 Splatting - principal idea • This last equation • can be rewritten in the following way: Splatting Kernel or “Splat” 4 Which can be computed analytically: known as footprint analytically
Splatting - principal idea • This last equation • can be rewritten in the following way: Splatting Kernel or “Splat” 4 Which can be computed analytically: known as footprint analytically
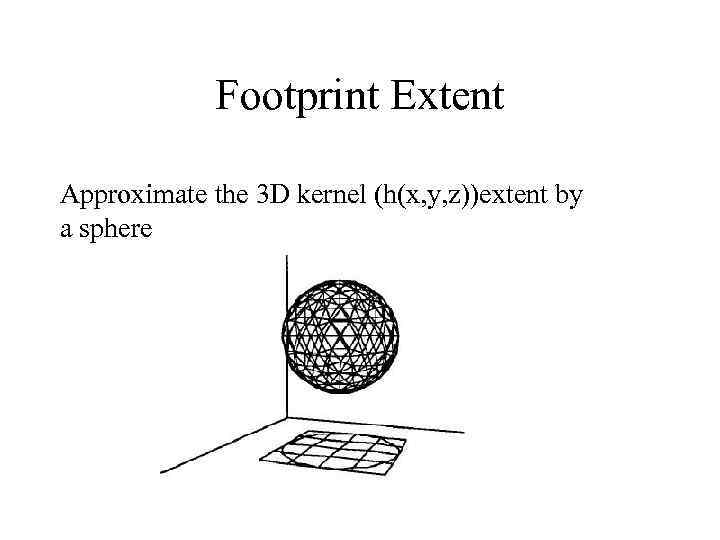 Footprint Extent Approximate the 3 D kernel (h(x, y, z))extent by a sphere
Footprint Extent Approximate the 3 D kernel (h(x, y, z))extent by a sphere
 Footprint Table A popular kernel is a three-dimensional Gaussian (radially symmetric) As 1 D integration of 3 D Gaussian is still a 2 D Gaussian – we can just skip the Z integration and evaluate the Gaussian function on 2 D image space after voxel projection Generic footprint table preprocessing
Footprint Table A popular kernel is a three-dimensional Gaussian (radially symmetric) As 1 D integration of 3 D Gaussian is still a 2 D Gaussian – we can just skip the Z integration and evaluate the Gaussian function on 2 D image space after voxel projection Generic footprint table preprocessing
 View-dependent footprint It is possible to transform a sphere kernel into A ellipsoid • The projection of an ellipsoid is an ellipse • We need to transform the generic footprint table to the ellipse
View-dependent footprint It is possible to transform a sphere kernel into A ellipsoid • The projection of an ellipsoid is an ellipse • We need to transform the generic footprint table to the ellipse
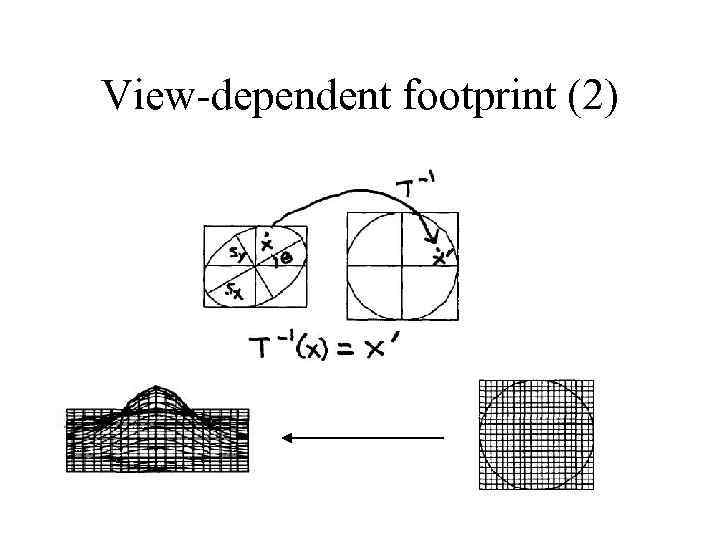 View-dependent footprint (2)
View-dependent footprint (2)
 Example Footprint at Different Resolutions
Example Footprint at Different Resolutions
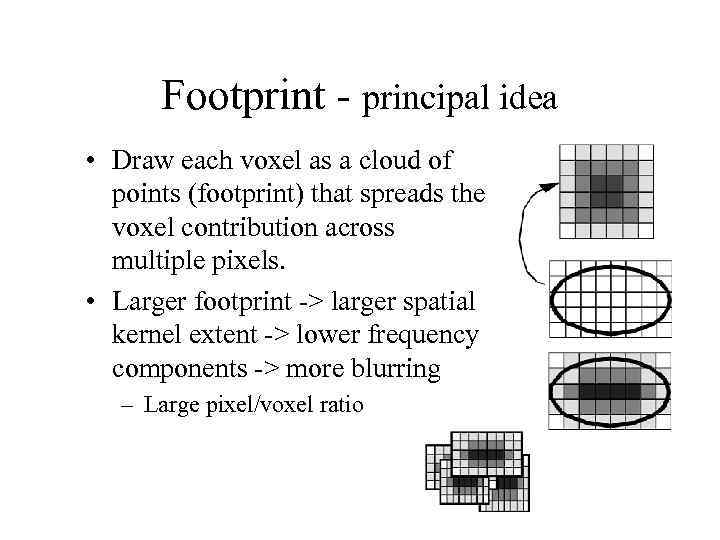 Footprint - principal idea • Draw each voxel as a cloud of points (footprint) that spreads the voxel contribution across multiple pixels. • Larger footprint -> larger spatial kernel extent -> lower frequency components -> more blurring – Large pixel/voxel ratio
Footprint - principal idea • Draw each voxel as a cloud of points (footprint) that spreads the voxel contribution across multiple pixels. • Larger footprint -> larger spatial kernel extent -> lower frequency components -> more blurring – Large pixel/voxel ratio
 Rendering a Splat • Use texture mapping hardware to resample footprint table (either single density channel or separate classified r, g, b, a channels) • Or, use Fast. Splats to render each splat as a graphics primitive of itself
Rendering a Splat • Use texture mapping hardware to resample footprint table (either single density channel or separate classified r, g, b, a channels) • Or, use Fast. Splats to render each splat as a graphics primitive of itself
 Splatting - efficiency • “footprint” - splatted (integrated) kernel • if interpolation kernel is isotropic (spherical) then its footprint is independent of the view point (for orthographic viewing) • for perspective - footprint can be approximated with an ellipse • Hence, for common cases, we can pre-integrate it (efficient!) • for perspective projection, to approximate, we have to compute the orientation of the ellipse
Splatting - efficiency • “footprint” - splatted (integrated) kernel • if interpolation kernel is isotropic (spherical) then its footprint is independent of the view point (for orthographic viewing) • for perspective - footprint can be approximated with an ellipse • Hence, for common cases, we can pre-integrate it (efficient!) • for perspective projection, to approximate, we have to compute the orientation of the ellipse
 Splatting - Highlights • Footprints can be pre-integrated – fast voxel projection • Advantages over ray-casting: – – Fast: voxel interpolation is in 2 D on screen More accurate integration (analytic for X-ray) More accurate reconstruction (afford better kernels) Only relevant voxels must be projected
Splatting - Highlights • Footprints can be pre-integrated – fast voxel projection • Advantages over ray-casting: – – Fast: voxel interpolation is in 2 D on screen More accurate integration (analytic for X-ray) More accurate reconstruction (afford better kernels) Only relevant voxels must be projected
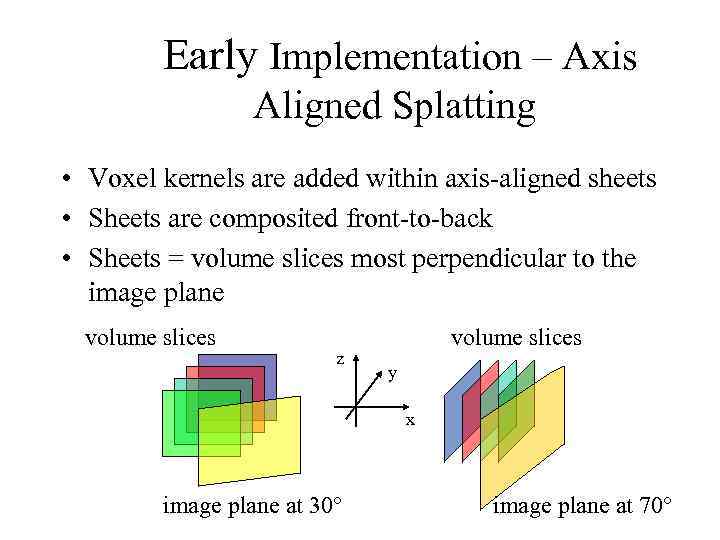 Early Implementation – Axis Aligned Splatting • Voxel kernels are added within axis-aligned sheets • Sheets are composited front-to-back • Sheets = volume slices most perpendicular to the image plane volume slices z volume slices y x image plane at 30° image plane at 70°
Early Implementation – Axis Aligned Splatting • Voxel kernels are added within axis-aligned sheets • Sheets are composited front-to-back • Sheets = volume slices most perpendicular to the image plane volume slices z volume slices y x image plane at 30° image plane at 70°
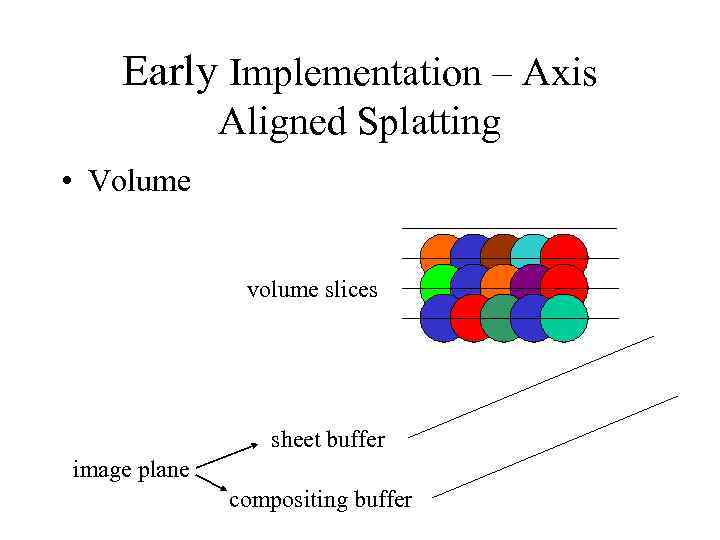 Early Implementation – Axis Aligned Splatting • Volume volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Volume volume slices sheet buffer image plane compositing buffer
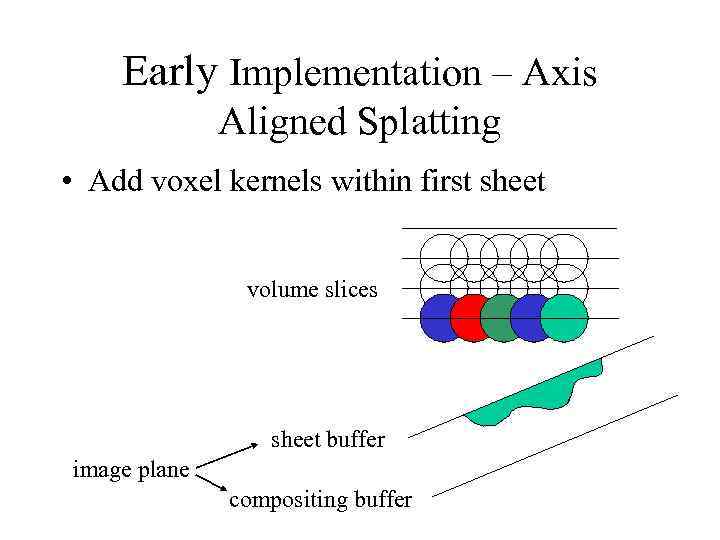 Early Implementation – Axis Aligned Splatting • Add voxel kernels within first sheet volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Add voxel kernels within first sheet volume slices sheet buffer image plane compositing buffer
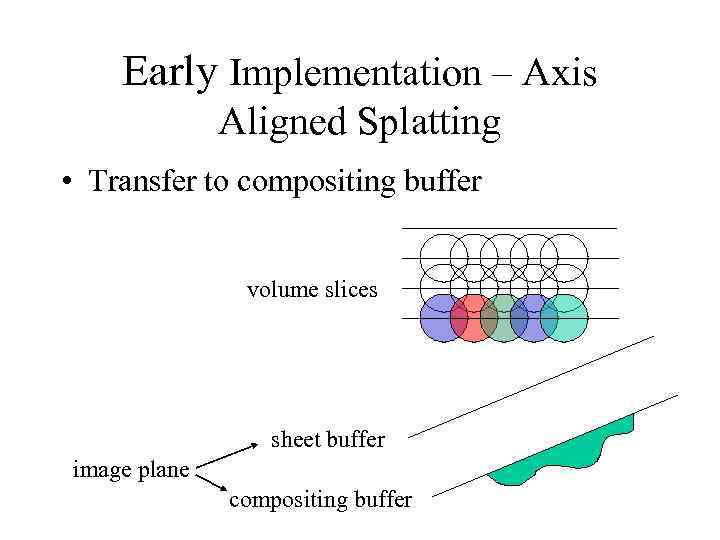 Early Implementation – Axis Aligned Splatting • Transfer to compositing buffer volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Transfer to compositing buffer volume slices sheet buffer image plane compositing buffer
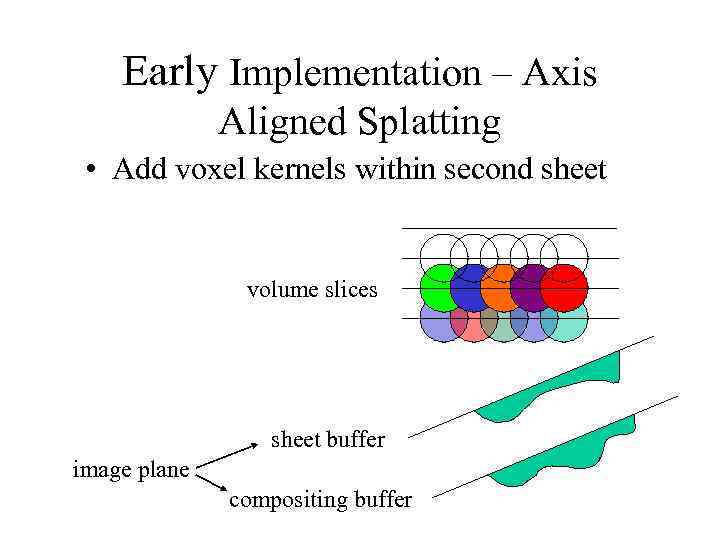 Early Implementation – Axis Aligned Splatting • Add voxel kernels within second sheet volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Add voxel kernels within second sheet volume slices sheet buffer image plane compositing buffer
 Early Implementation – Axis Aligned Splatting • Composite sheet with compositing buffer volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Composite sheet with compositing buffer volume slices sheet buffer image plane compositing buffer
 Early Implementation – Axis Aligned Splatting • Add voxel kernels within third sheet volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Add voxel kernels within third sheet volume slices sheet buffer image plane compositing buffer
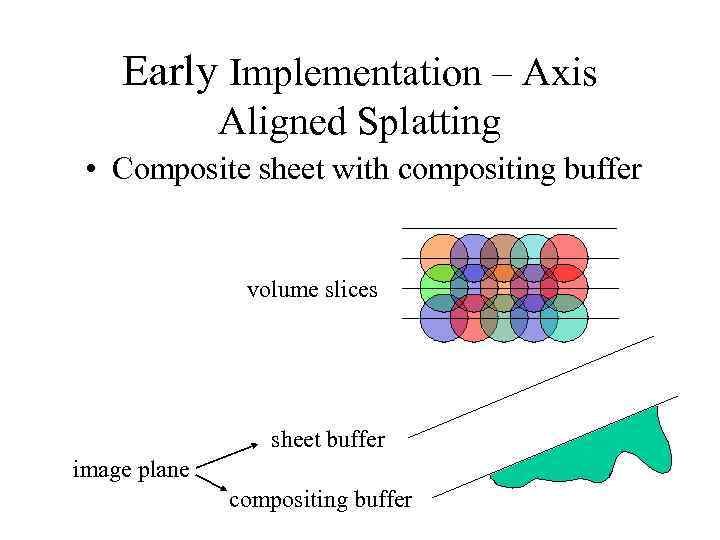 Early Implementation – Axis Aligned Splatting • Composite sheet with compositing buffer volume slices sheet buffer image plane compositing buffer
Early Implementation – Axis Aligned Splatting • Composite sheet with compositing buffer volume slices sheet buffer image plane compositing buffer
 What Doesn’t Work? • Mathematically, the early splatting methods only work for Xray type of rendering, where voxel ordering is not important – Bad approximation for other types of optical models • Object ordering is important in volume rendering, front objects hide back objects – need to composite splats in proper order, else we get bleeding of background objects into the image (color bleeding!) • Axis- aligned approach add all splats that fall within a volume slice most parallel to the image plane, composite these sheets in front- to- back order – Incorrect accumulating on axis-aligned face cause popping • A better approximation with Riemann sum is to use the imagealigned sheet-based approach
What Doesn’t Work? • Mathematically, the early splatting methods only work for Xray type of rendering, where voxel ordering is not important – Bad approximation for other types of optical models • Object ordering is important in volume rendering, front objects hide back objects – need to composite splats in proper order, else we get bleeding of background objects into the image (color bleeding!) • Axis- aligned approach add all splats that fall within a volume slice most parallel to the image plane, composite these sheets in front- to- back order – Incorrect accumulating on axis-aligned face cause popping • A better approximation with Riemann sum is to use the imagealigned sheet-based approach
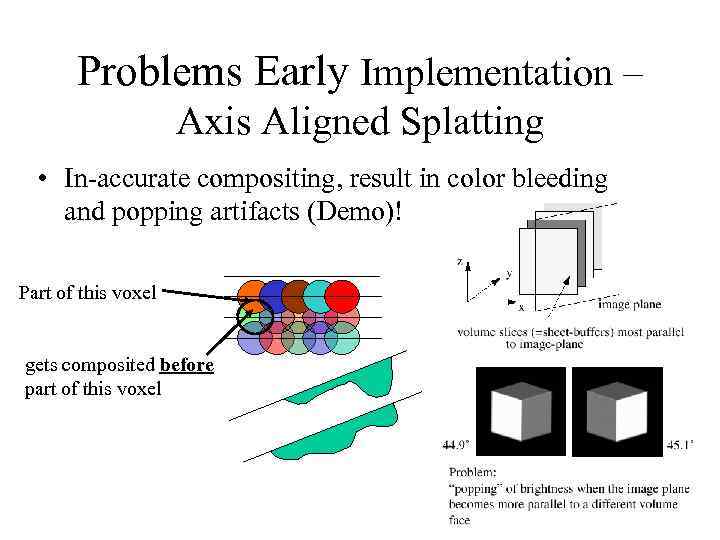 Problems Early Implementation – Axis Aligned Splatting • In-accurate compositing, result in color bleeding and popping artifacts (Demo)! Part of this voxel gets composited before part of this voxel
Problems Early Implementation – Axis Aligned Splatting • In-accurate compositing, result in color bleeding and popping artifacts (Demo)! Part of this voxel gets composited before part of this voxel
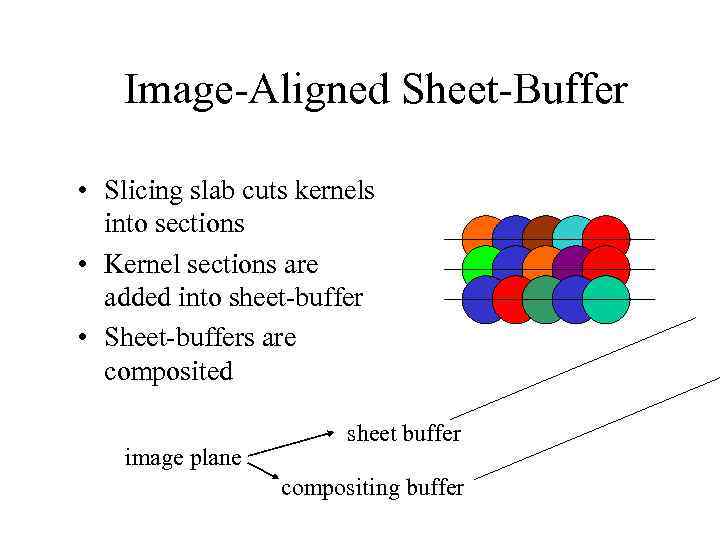 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
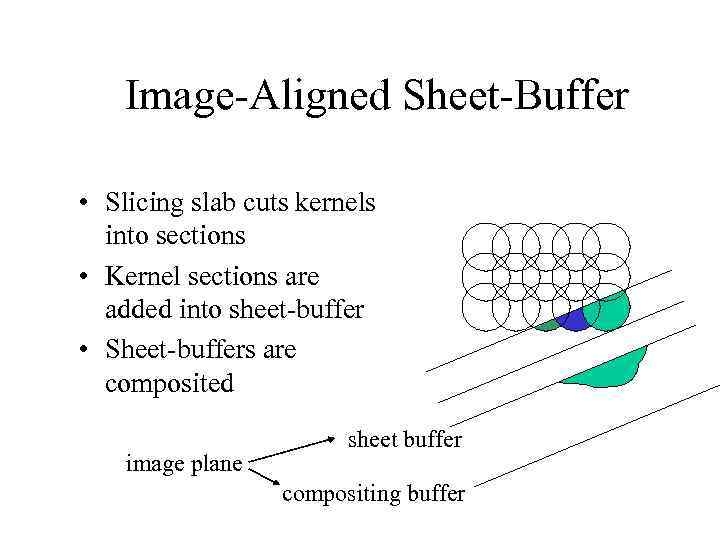 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
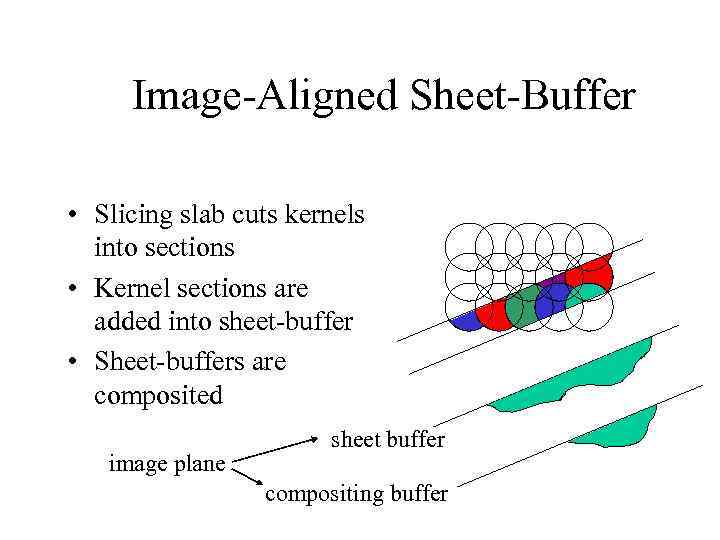 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
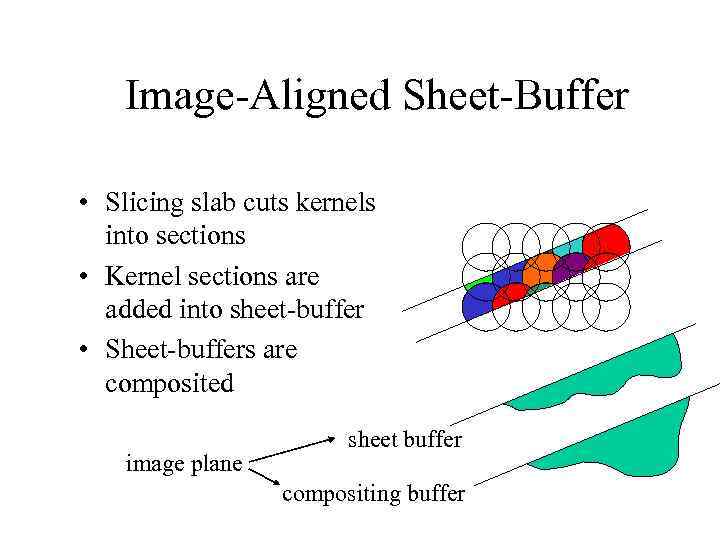 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
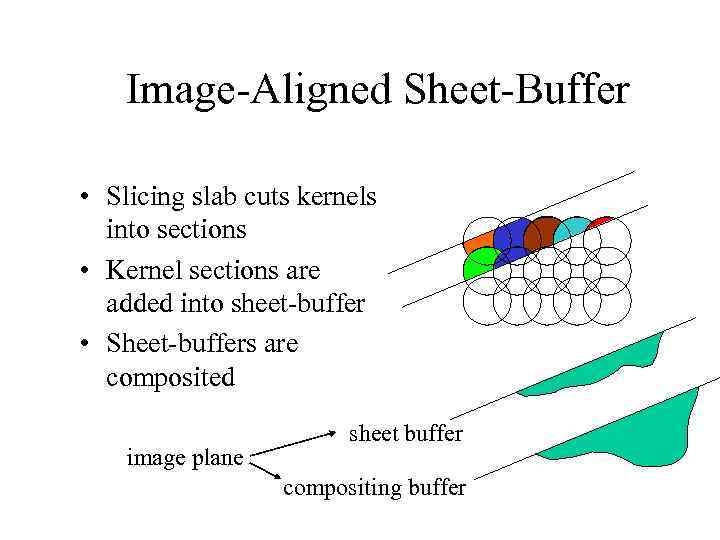 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
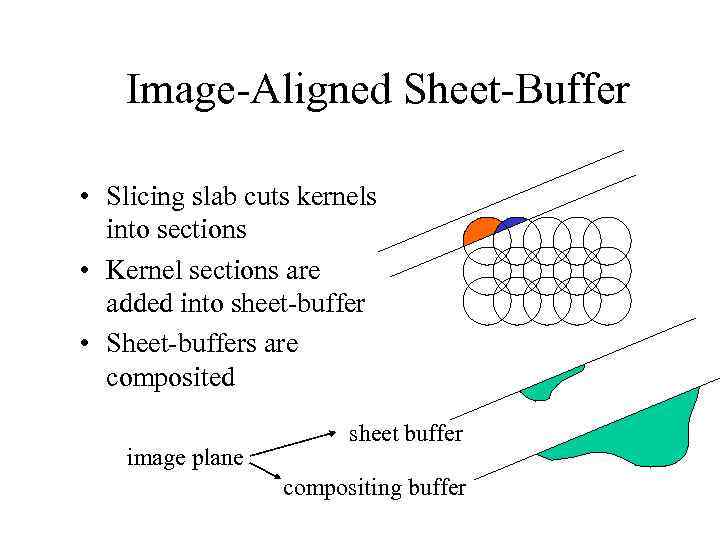 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
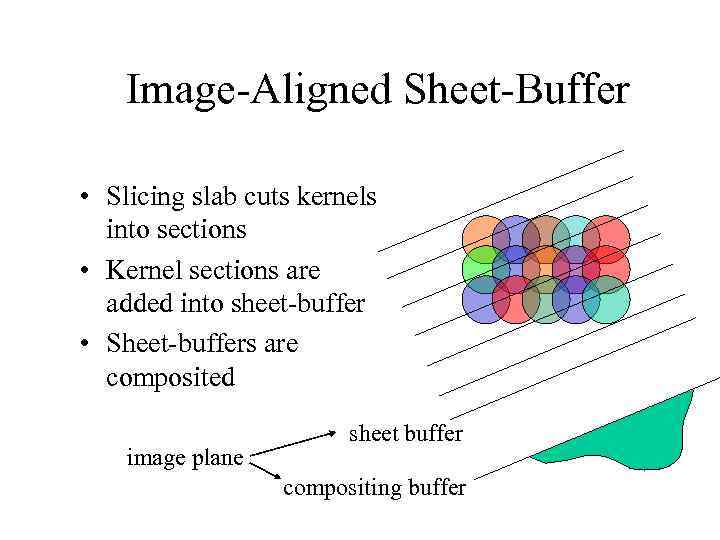 Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
Image-Aligned Sheet-Buffer • Slicing slab cuts kernels into sections • Kernel sections are added into sheet-buffer • Sheet-buffers are composited image plane sheet buffer compositing buffer
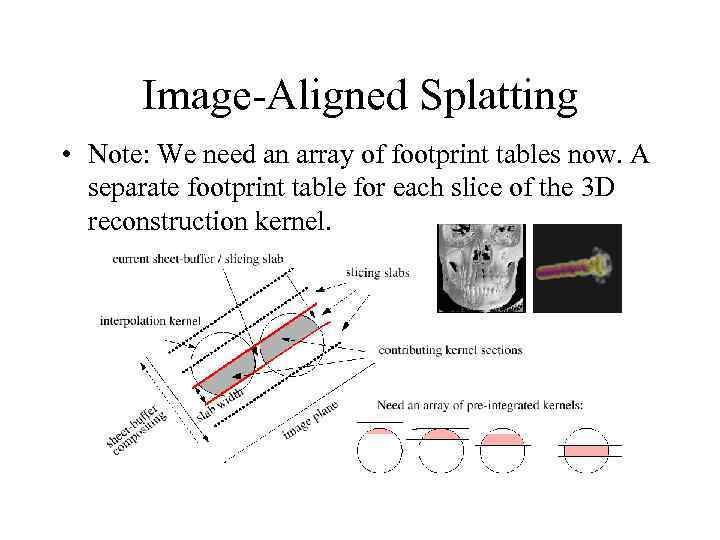 Image-Aligned Splatting • Note: We need an array of footprint tables now. A separate footprint table for each slice of the 3 D reconstruction kernel.
Image-Aligned Splatting • Note: We need an array of footprint tables now. A separate footprint table for each slice of the 3 D reconstruction kernel.
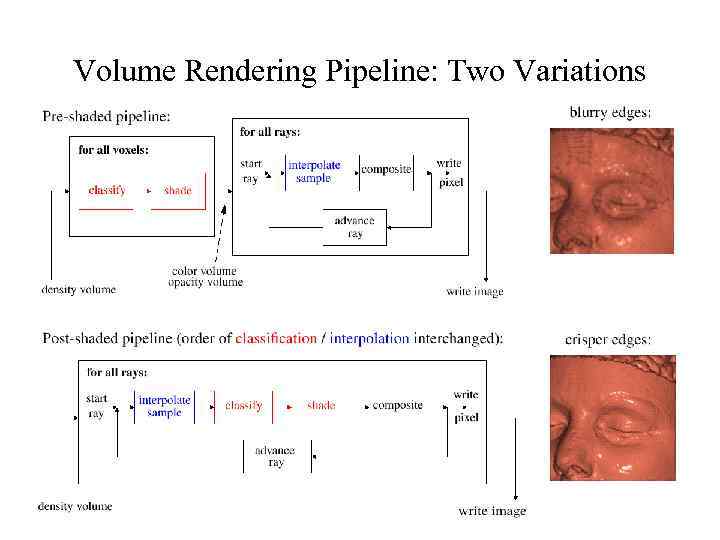 Volume Rendering Pipeline: Two Variations
Volume Rendering Pipeline: Two Variations
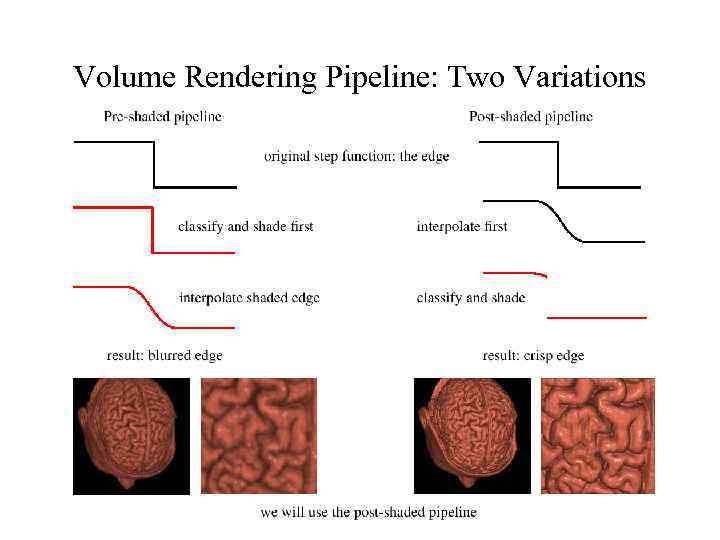 Volume Rendering Pipeline: Two Variations
Volume Rendering Pipeline: Two Variations
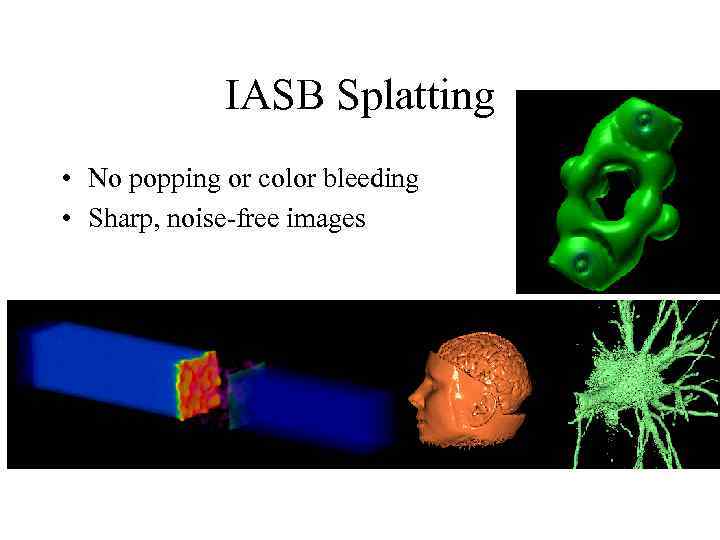 IASB Splatting • No popping or color bleeding • Sharp, noise-free images
IASB Splatting • No popping or color bleeding • Sharp, noise-free images
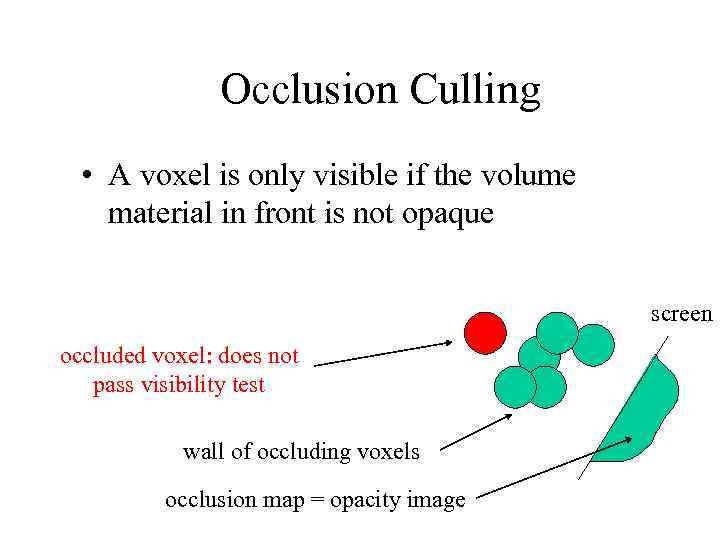 Occlusion Culling • A voxel is only visible if the volume material in front is not opaque screen occluded voxel: does not pass visibility test wall of occluding voxels occlusion map = opacity image
Occlusion Culling • A voxel is only visible if the volume material in front is not opaque screen occluded voxel: does not pass visibility test wall of occluding voxels occlusion map = opacity image
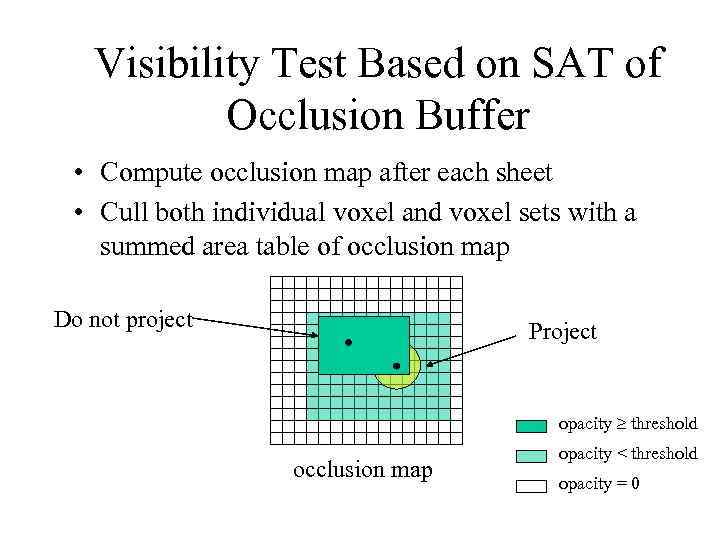 Visibility Test Based on SAT of Occlusion Buffer • Compute occlusion map after each sheet • Cull both individual voxel and voxel sets with a summed area table of occlusion map Do not project Project opacity threshold occlusion map opacity < threshold opacity = 0
Visibility Test Based on SAT of Occlusion Buffer • Compute occlusion map after each sheet • Cull both individual voxel and voxel sets with a summed area table of occlusion map Do not project Project opacity threshold occlusion map opacity < threshold opacity = 0
 Occlusion Culling • Build a summed area table (SAT) from the opacity buffer • To test whether a rectangular region is opaque or not, check the four corners • Can cull voxel sets directly
Occlusion Culling • Build a summed area table (SAT) from the opacity buffer • To test whether a rectangular region is opaque or not, check the four corners • Can cull voxel sets directly
 Anti-aliasing • Needed to preserve small features • Needed for the diverging rays in perspective • In splatting, resize the footprint according to depth Aliased anti-aliased
Anti-aliasing • Needed to preserve small features • Needed for the diverging rays in perspective • In splatting, resize the footprint according to depth Aliased anti-aliased
 Motion Blur • Stretch the reconstruction kernel in the direction of movement. • Stretch the splat footprint in the direction of the projected movement (2 D).
Motion Blur • Stretch the reconstruction kernel in the direction of movement. • Stretch the splat footprint in the direction of the projected movement (2 D).
 Camera Depth-of-Field • Two possible approaches: – Low-pass filter the splats – Low-pass filter the sheets Plain with Depth-of-Field
Camera Depth-of-Field • Two possible approaches: – Low-pass filter the splats – Low-pass filter the sheets Plain with Depth-of-Field
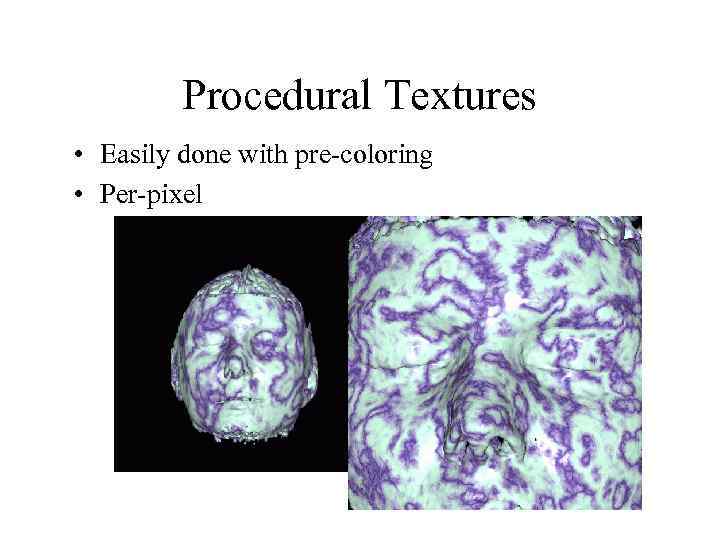 Procedural Textures • Easily done with pre-coloring • Per-pixel
Procedural Textures • Easily done with pre-coloring • Per-pixel
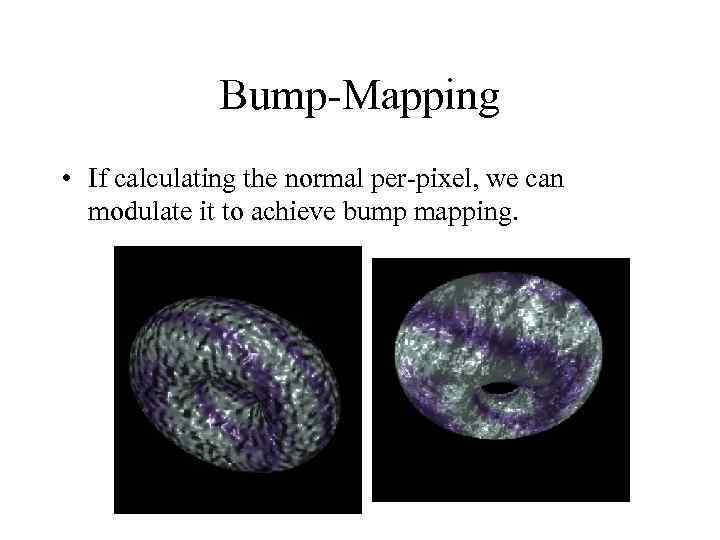 Bump-Mapping • If calculating the normal per-pixel, we can modulate it to achieve bump mapping.
Bump-Mapping • If calculating the normal per-pixel, we can modulate it to achieve bump mapping.
 Per-pixel Classification • Per-pixel classification can be based on gray scale, position, gradient, or. . . 7. 25 sec 9. 41 sec (procedural) 7. 99 sec
Per-pixel Classification • Per-pixel classification can be based on gray scale, position, gradient, or. . . 7. 25 sec 9. 41 sec (procedural) 7. 99 sec
 Scan-Converting A Splat • Scan-convert an arbitrary-size radially symmetric 2 D function centered at arbitrary position – circular or elliptical • Texture mapping hardware is not the solution • We want a hardware accelerated splat or point primitive
Scan-Converting A Splat • Scan-convert an arbitrary-size radially symmetric 2 D function centered at arbitrary position – circular or elliptical • Texture mapping hardware is not the solution • We want a hardware accelerated splat or point primitive
 Fast Splats Fast. Splat • We desire – fast scan conversion – minimum or controllable errors – compact storage – simple integer operation
Fast Splats Fast. Splat • We desire – fast scan conversion – minimum or controllable errors – compact storage – simple integer operation
 Fast. Splats · · 1 D Linear 1 D Squared 2 D 1 D with Radius Look Up Table (RLUT)
Fast. Splats · · 1 D Linear 1 D Squared 2 D 1 D with Radius Look Up Table (RLUT)
 1 D Linear, 1 D Squared Fast. Splats • On the radial line 1 D Linear Fast. Splat, indexed by rx, y 1 D Squared Fast. Splat, indexed by r 2 x, y (x, y) (x+1, y) (xo, yo)
1 D Linear, 1 D Squared Fast. Splats • On the radial line 1 D Linear Fast. Splat, indexed by rx, y 1 D Squared Fast. Splat, indexed by r 2 x, y (x, y) (x+1, y) (xo, yo)
 1 D Squared Fast. Splat (Elliptical) • For elliptical kernels, if we define a canonical radius: • The incremental scan-conversion still works at the same low cost
1 D Squared Fast. Splat (Elliptical) • For elliptical kernels, if we define a canonical radius: • The incremental scan-conversion still works at the same low cost
 Fast. Splats Ö 1 D Linear Ö 1 D Squared · 2 D • 1 D with Radius Look Up Table (RLUT)
Fast. Splats Ö 1 D Linear Ö 1 D Squared · 2 D • 1 D with Radius Look Up Table (RLUT)
 2 D Fast. Splat (Bit. Blt, Vox. Blt) • No run-time computation Pre-rasterized footprint with center at (xo, yo), radius r Pre-rasterized footprints for all possible center positions, radius r Snap splat center to a k by k subpixel grid
2 D Fast. Splat (Bit. Blt, Vox. Blt) • No run-time computation Pre-rasterized footprint with center at (xo, yo), radius r Pre-rasterized footprints for all possible center positions, radius r Snap splat center to a k by k subpixel grid
 2 D Fast. Splats • No run-time computation Pre-rasterized footprints for all possible center positions, for all possible radii Snap splat center to a k by k subpixel grid Allow for a set of radius values
2 D Fast. Splats • No run-time computation Pre-rasterized footprints for all possible center positions, for all possible radii Snap splat center to a k by k subpixel grid Allow for a set of radius values
 2 D Fast. Splats (2) • The storage need: • When storage is limited, the quality is limited too • [Mora’ 00], similar
2 D Fast. Splats (2) • The storage need: • When storage is limited, the quality is limited too • [Mora’ 00], similar
 Fast. Splats Ö 1 D Linear Ö 1 D Squared Ö 2 D • 1 D with Radius Look Up Table (RLUT)
Fast. Splats Ö 1 D Linear Ö 1 D Squared Ö 2 D • 1 D with Radius Look Up Table (RLUT)
 1 D RLUT Fast. Splat • For hardware, we need finer parallelism than scan-line
1 D RLUT Fast. Splat • For hardware, we need finer parallelism than scan-line
 1 D Fast. Splat with RLUT
1 D Fast. Splat with RLUT
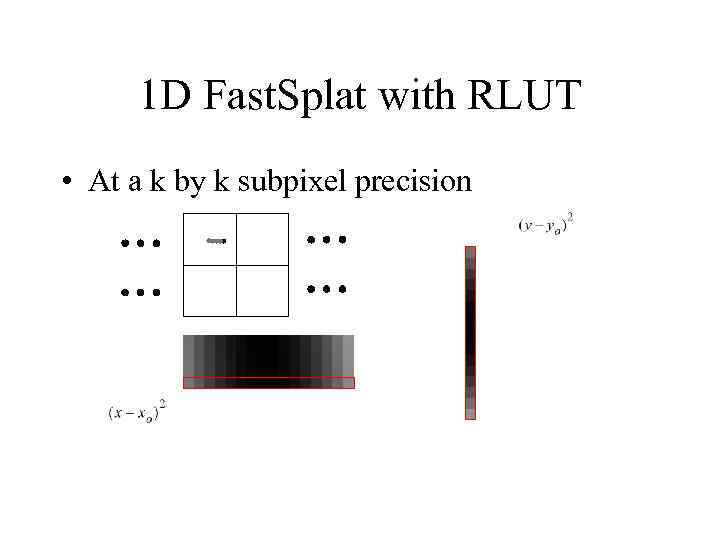
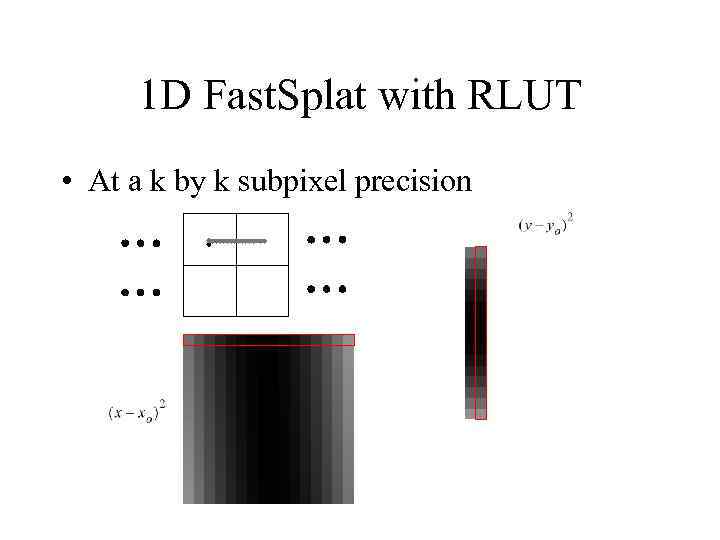
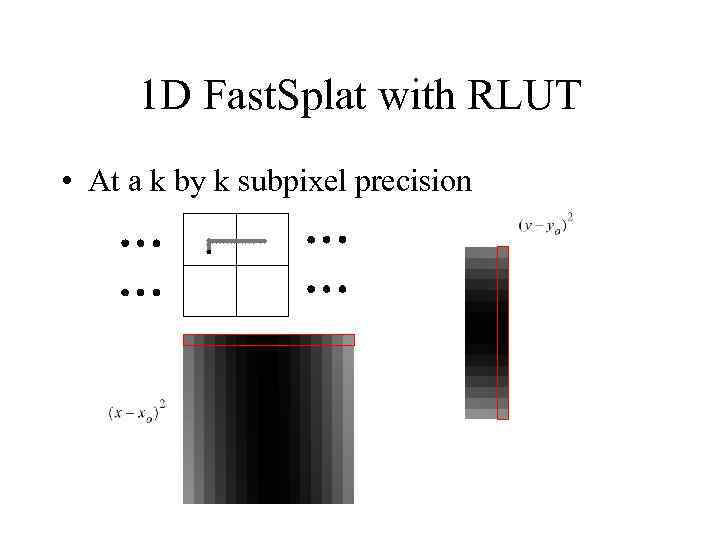
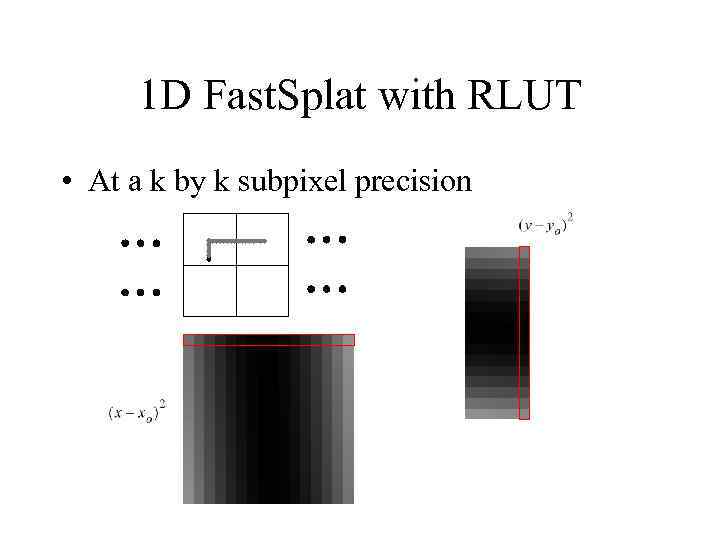
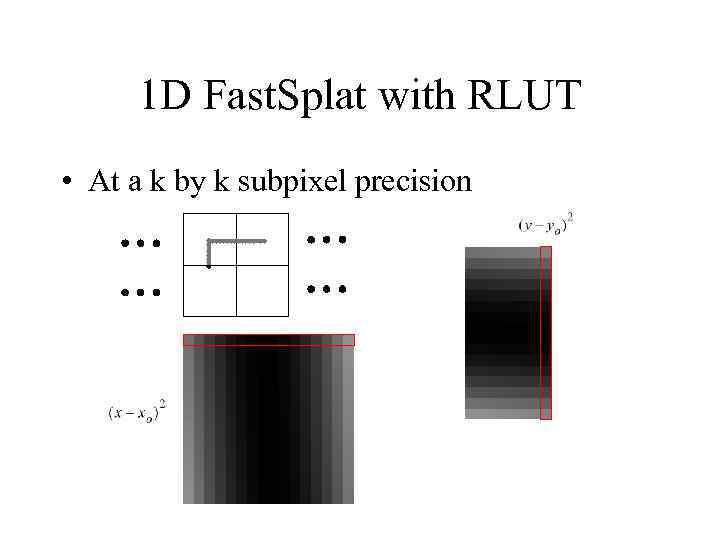
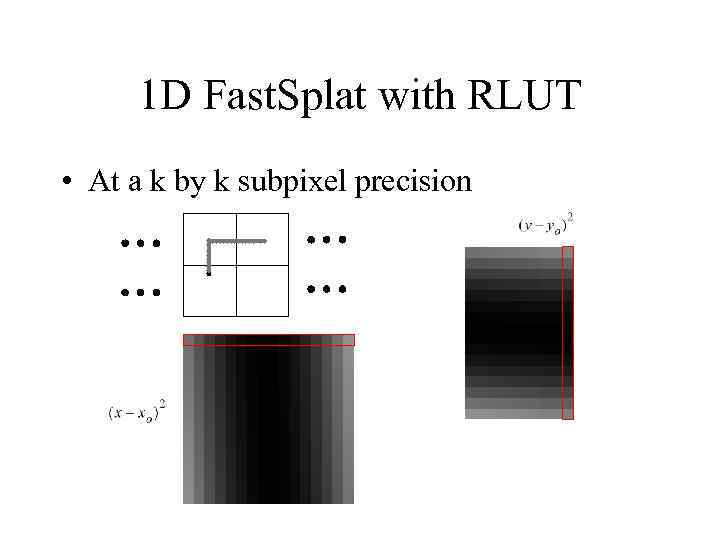
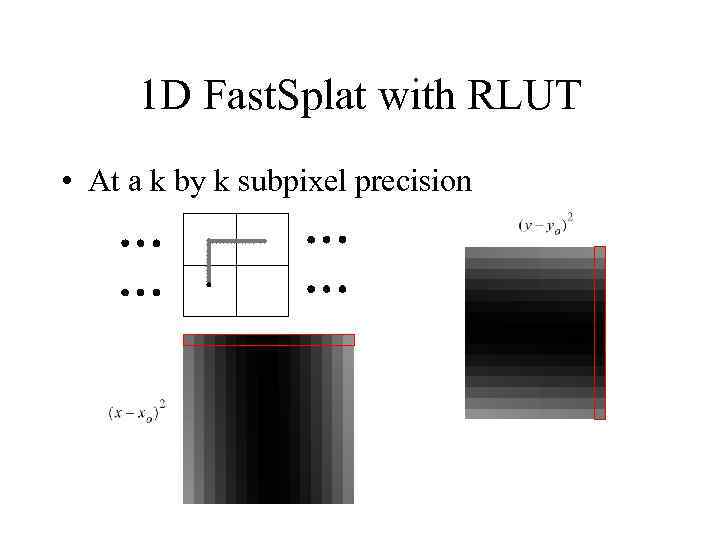
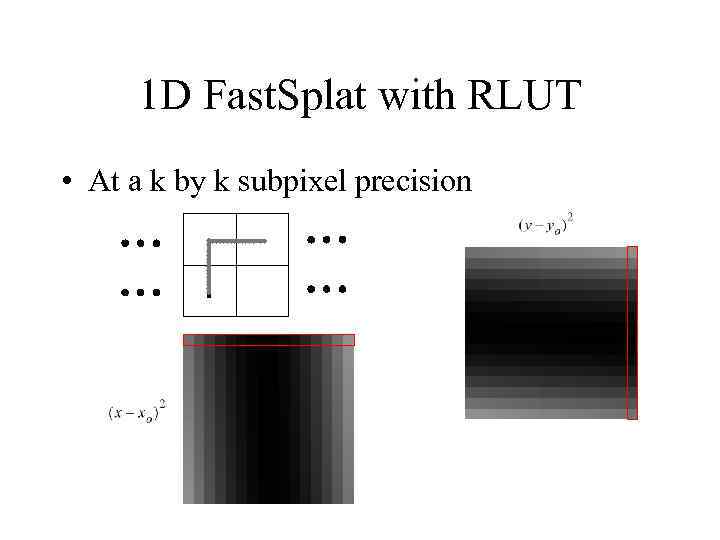
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
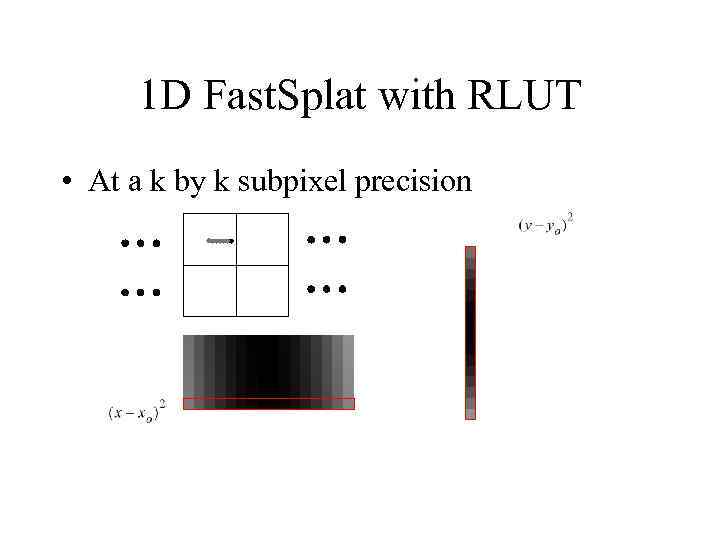 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
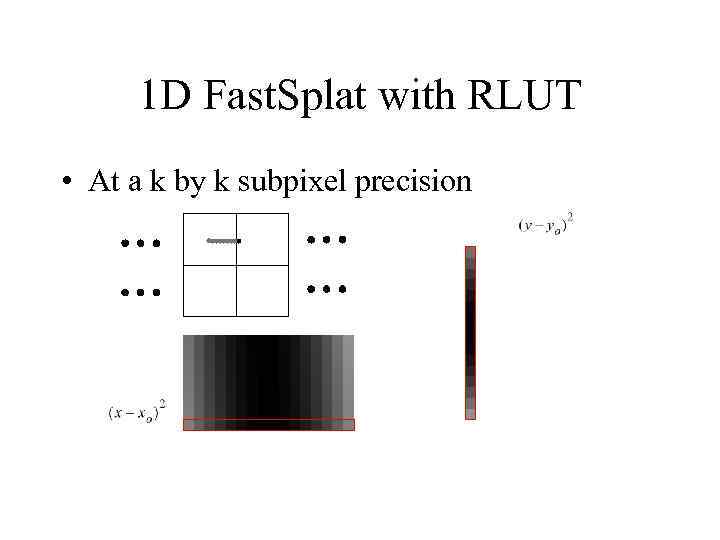 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
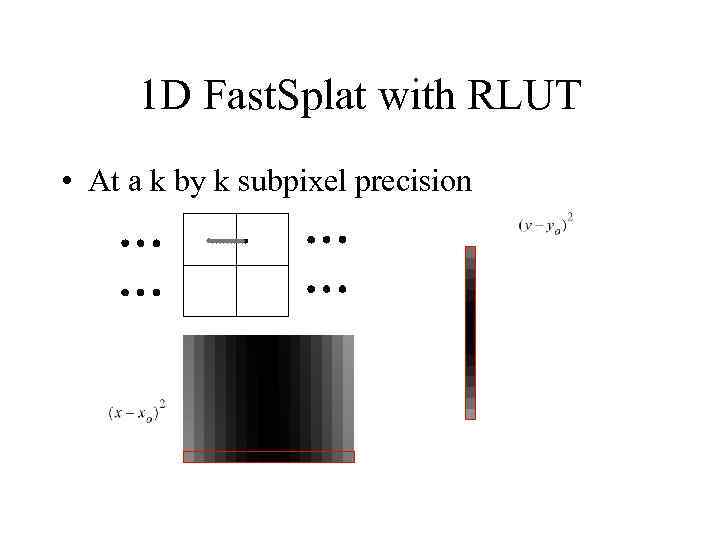 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
 1 D Fast. Splat with RLUT • At a k by k subpixel precision
1 D Fast. Splat with RLUT • At a k by k subpixel precision
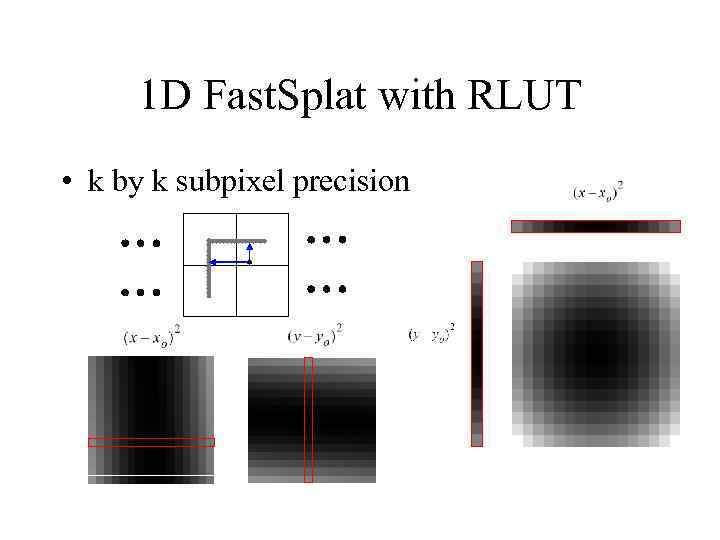 1 D Fast. Splat with RLUT • k by k subpixel precision
1 D Fast. Splat with RLUT • k by k subpixel precision
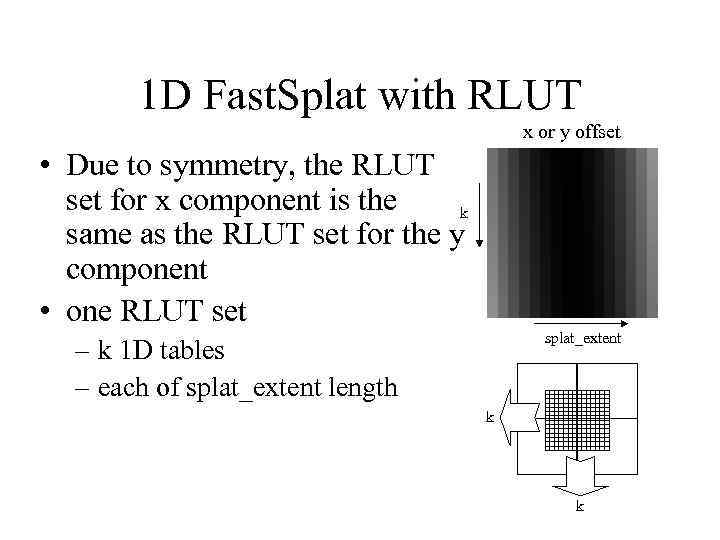 1 D Fast. Splat with RLUT x or y offset • Due to symmetry, the RLUT set for x component is the k same as the RLUT set for the y component • one RLUT set splat_extent – k 1 D tables – each of splat_extent length k k
1 D Fast. Splat with RLUT x or y offset • Due to symmetry, the RLUT set for x component is the k same as the RLUT set for the y component • one RLUT set splat_extent – k 1 D tables – each of splat_extent length k k
 Comparisons Among the Fast. Splats • 1 D Linear: very accurate, compact, slow • 1 D Squared: accurate, compact, fast • 1 D RLUT: accurate, compact, intended for hardware • 2 D Fast. Splat: can be very fast, accurate and compact under constrained conditions
Comparisons Among the Fast. Splats • 1 D Linear: very accurate, compact, slow • 1 D Squared: accurate, compact, fast • 1 D RLUT: accurate, compact, intended for hardware • 2 D Fast. Splat: can be very fast, accurate and compact under constrained conditions


