Список литературы 1 Н Вирт Алгоритмы и структуры

Список литературы 1. Н. Вирт. «Алгоритмы и структуры данных» , 1989. 2. Д. Кнут. «Искусство программирования для ЭВМ» , том 1 и 3, 1976 -78. 3. Т. Кормен, Ч. Лейзерсон, Р. Ривест. «Алгоритмы: построение и анализ» , 2001, 2004, 2009, 2011. 4. Р. Сержвик. «Фундаментальные алгоритмы на С++» , 2002. 5. Е. В. Курапова, Е. П. Мачикина. «Структуры и алгоритмы обработки данных» , 2006. 6. Е. В. Курапова, Е. П. Мачикина. «Основные методы кодирования данных» , 2010.

Курсовая работа Папка KURAPOVACURS_WORKNEWBASE Файлы CURS_WORK. txt opn. cpp test. Base 1. dat test. Base 2. dat test. Base 3. dat test. Base 4. dat

Постановка задачи курсовой работы Хранящуюся в файле базу данных (4000 записей) загрузить динамически в оперативную память компьютера, вывести на экран по 20 записей (строк) на странице с возможностью отказа от просмотра и построить индексный массив, упорядочивающий данные в соответствии с заданным условием упорядочения, используя указанный метод сортировки. Предусмотреть возможность поиска по ключу в упорядоченной базе, в результате которого из записей с одинаковым ключом формируется очередь, содержимое очереди выводится на экран. Вариант задания задается с помощью чисел B, C, S, где B - номер базы данных; C - вариант условия упорядочения для этой базы данных; S - метод сортировки;

Ключ поиска указывается вместе с условием упорядочения и, как правило, представляет собой упрощенный вариант ключа сортировки. Числа B, C, S определяются с помощью таблицы соответствия вариантов (50 Вариантов). B = 1 (файл base 1. dat) Библиогpафическая база данных "Жизнь замечательных людей" B = 2 (файл base 2. dat) База данных "Пpедпpиятие" B = 3 (файл base 3. dat) База данных "Обманутые вкладчики" B = 4 (файл base 4. dat) База данных "Населенный пункт"

Пирамидальная сортировка или метод Вильямса - Флойда ( Williams, Floyd, 1964) Heap. Sort Пирамидальная сортировка основана на алгоритме построения пирамиды. Определение Последовательность a. L , a. L+1 , … , a. R называется пирамидой, если неравенство ai ≤ min (a 2 i , a 2 i+1 ) выполняется для всех i, для которых хотя бы один из элементов a 2 i и a 2 i+1 существует.

Пример 2 3 4 5 6 7 8 - пирамида 3 2 6 3 4 5 7 пирамида Свойства пирамиды 1 2 3 4 5 6 7 - не 1. Двустороннее усечение: Если последовательность a. L, a. L+1, . . , а. R-1, a. R – пирамида, то a. L+1, . . , a. R-1 тоже пирамида. 2. Если a 1, a 2, . . , an – пирамида, то а 1 – минимальный элемент пирамиды. 3. Если a 1, . . , an – произвольная последовательность, то an/2, . . , an – пирамида.

Построение пирамиды Пусть a. L+1, …, a. R - пирамида, необходимо добавить элемент Х, чтобы получить новую пирамиду a. L, …, a. R. Новый элемент добавляем в начало, расширяя последовательность влево. Если a. L удовлетворяет условию пирамиды, то пирамида построена. Иначе найдутся такие a 2 L или a 2 L+1 , что не будут удовлетворять условию пирамиды. Возьмем минимальный элемент из a 2 L и a 2 L+1 , обозначим его за aj и обменяем с a. L.

В результате получим a’L ≤ a 2 L и a’L ≤ a 2 L+1 , что удовлетворяет условию пирамиды. Теперь элемент Х попал на место aj и для него необходимо проверить условие пирамиды, и так до конца массива. Пример: 1 2 3 4 5 6 7 8 3 2 6 3 4 5 7 Пирамида 6 3 2 6 3 4 5 7 2 3 6 6 3 4 5 7 2 3 4 6 3 6 5 7 Пирамида

Построение пирамиды (L, R) Алгоритм на псевдокоде a. L+1, …, a R – на входе пирамида (L+1, R) a. L – новый элемент X : = a. L, i : = L DO j : = 2 i IF ( j>R) OD FI IF ( j

•

Пирамидальная сортировка (Heap. Sort) Первый этап. Построение пирамиды из элементов массива. В соответствии со свойством 3 правая часть массива уже пирамида. Будем добавлять по одному элементу слева, расширяя пирамиду, пока в нее не войдут все элементы массива. Второй этап. По свойству 2 в пирамиде первый элемент минимальный. Производим двустороннее усечение пирамиды: уберем элементы а 1 и аn. По свойству 1 a 2, . . , an-1 – пирамида. Поставим элемент а 1 на последнее место, а элемент аn добавим к пирамиде a 2, . . , an-1. Отсекаем последний элемент и повторяем действия, пока пирамида не исчезнет.

Пирамидальная сортировка (Heap. Sort) Алгоритм на псевдокоде | L : = n/2 | DO ( L>0 ) 1 | Построение пирамиды (L, n) | L : = L-1 | OD | R : = n | DO ( R>1) 2 | a 1↔a. R | R : = R-1 | Построение пирамиды (1, R) | OD

1 2 3 4 5 6 7 8 К У Р А П О В А Пирамида А П О В А Пирамида Р А П О В А П О Р А Пирамида У В А П О Р А А В У П О Р А А В А П О Р У Пирамида К А В А П О Р У А К В А П О Р У А А В К П О Р У Пирамида

1 2 3 4 5 6 7 8 А А В К П О Р У У А В К П О Р А А У В К П О Р А К В У П О Р Пирамида Р К В У П О А В К Р У П О Пирамида В К О У П Р Р К О У П В К Р О У П Пирамида К П О У Р

1 2 3 4 5 Р П О У К О П Р У П Р О П У Р Р У П Р У У Пирамида У Р П О К В А A

•

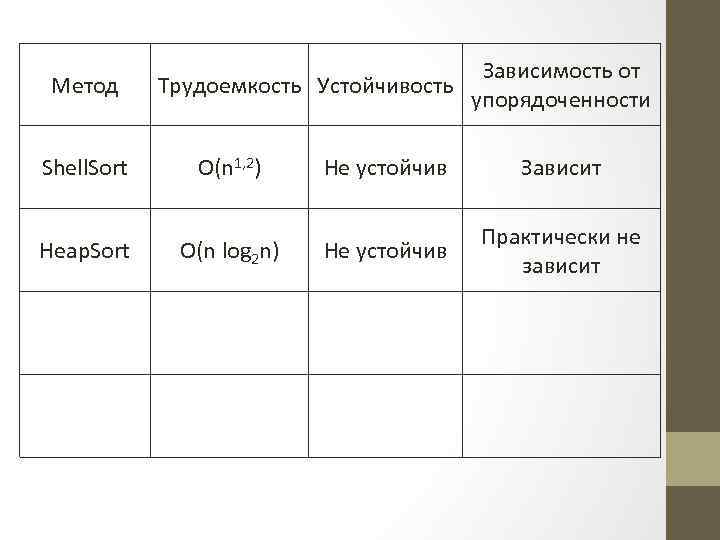Метод Shell. Sort Heap. Sort Зависимость от Трудоемкость Устойчивость упорядоченности O(n 1, 2) O(n log 2 n) Не устойчив Зависит Не устойчив Практически не зависит