d362b86c07a9b37b3f4bdb73a2baea4e.ppt
- Количество слайдов: 2
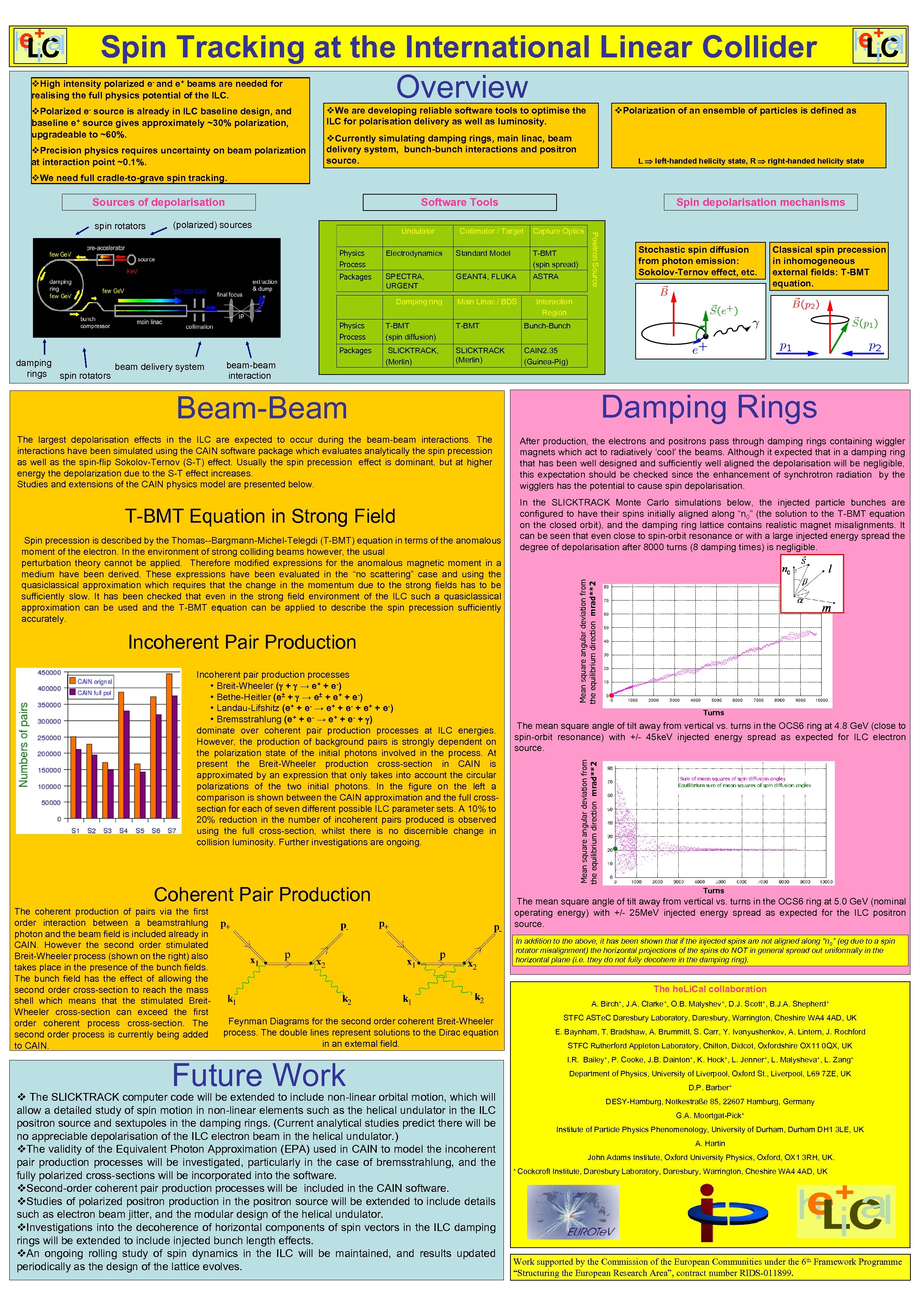 Spin Tracking at the International Linear Collider Overview v. High intensity polarized e- and e+ beams are needed for realising the full physics potential of the ILC. v. Polarized e- source is already in ILC baseline design, and baseline e+ source gives approximately ~30% polarization, upgradeable to ~60%. v. Precision physics requires uncertainty on beam polarization at interaction point ~0. 1%. v. We are developing reliable software tools to optimise the ILC for polarisation delivery as well as luminosity. v. Polarization of an ensemble of particles is defined as v. Currently simulating damping rings, main linac, beam delivery system, bunch-bunch interactions and positron source. L left-handed helicity state, R right-handed helicity state v. We need full cradle-to-grave spin tracking. Sources of depolarisation spin rotators Software Tools (polarized) sources Collimator / Target Capture Optics Physics Process Electrodynamics Standard Model T-BMT (spin spread) Packages SPECTRA, URGENT GEANT 4, FLUKA ASTRA Damping ring Main Linac / BDS T-BMT (spin diffusion) T-BMT Classical spin precession in inhomogeneous external fields: T-BMT equation. Bunch-Bunch Packages SLICKTRACK, (Merlin) SLICKTRACK (Merlin) CAIN 2. 35 (Guinea-Pig) beam-beam interaction Damping Rings Beam-Beam T-BMT Equation in Strong Field Spin precession is described by the Thomas--Bargmann-Michel-Telegdi (T-BMT) equation in terms of the anomalous moment of the electron. In the environment of strong colliding beams however, the usual perturbation theory cannot be applied. Therefore modified expressions for the anomalous magnetic moment in a medium have been derived. These expressions have been evaluated in the “no scattering” case and using the quasiclassical approximation which requires that the change in the momentum due to the strong fields has to be sufficiently slow. It has been checked that even in the strong field environment of the ILC such a quasiclassical approximation can be used and the T-BMT equation can be applied to describe the spin precession sufficiently accurately. After production, the electrons and positrons pass through damping rings containing wiggler magnets which act to radiatively ‘cool’ the beams. Although it expected that in a damping ring that has been well designed and sufficiently well aligned the depolarisation will be negligible, this expectation should be checked since the enhancement of synchrotron radiation by the wigglers has the potential to cause spin depolarisation. In the SLICKTRACK Monte Carlo simulations below, the injected particle bunches are configured to have their spins initially aligned along “n 0” (the solution to the T-BMT equation on the closed orbit), and the damping ring lattice contains realistic magnet misalignments. It can be seen that even close to spin-orbit resonance or with a large injected energy spread the degree of depolarisation after 8000 turns (8 damping times) is negligible. Mean square angular deviation from the equilibrium direction mrad**2 The largest depolarisation effects in the ILC are expected to occur during the beam-beam interactions. The interactions have been simulated using the CAIN software package which evaluates analytically the spin precession as well as the spin-flip Sokolov-Ternov (S-T) effect. Usually the spin precession effect is dominant, but at higher energy the depolarization due to the S-T effect increases. Studies and extensions of the CAIN physics model are presented below. Incoherent Pair Production Coherent Pair Production Turns The mean square angle of tilt away from vertical vs. turns in the OCS 6 ring at 4. 8 Ge. V (close to spin-orbit resonance) with +/- 45 ke. V injected energy spread as expected for ILC electron source. Mean square angular deviation from the equilibrium direction mrad**2 Incoherent pair production processes • Breit-Wheeler ( + → e+ + e-) • Bethe-Heitler (e± + → e± + e+ + e-) • Landau-Lifshitz (e+ + e- → e+ + e- + e+ + e-) • Bremsstrahlung (e+ + e- → e+ + e- + ) dominate over coherent pair production processes at ILC energies. However, the production of background pairs is strongly dependent on the polarization state of the initial photons involved in the process. At present the Breit-Wheeler production cross-section in CAIN is approximated by an expression that only takes into account the circular polarizations of the two initial photons. In the figure on the left a comparison is shown between the CAIN approximation and the full crosssection for each of seven different possible ILC parameter sets. A 10% to 20% reduction in the number of incoherent pairs produced is observed using the full cross-section, whilst there is no discernible change in collision luminosity. Further investigations are ongoing. The coherent production of pairs via the first order interaction between a beamstrahlung photon and the beam field is included already in CAIN. However the second order stimulated Breit-Wheeler process (shown on the right) also takes place in the presence of the bunch fields. The bunch field has the effect of allowing the second order cross-section to reach the mass shell which means that the stimulated Breit. Wheeler cross-section can exceed the first order coherent process cross-section. The second order process is currently being added to CAIN. Stochastic spin diffusion from photon emission: Sokolov-Ternov effect, etc. Interaction Region Physics Process damping beam delivery system rings spin rotators Positron Source Undulator Spin depolarisation mechanisms Turns The mean square angle of tilt away from vertical vs. turns in the OCS 6 ring at 5. 0 Ge. V (nominal operating energy) with +/- 25 Me. V injected energy spread as expected for the ILC positron source. In addition to the above, it has been shown that if the injected spins are not aligned along “n 0” (eg due to a spin rotator misalignment) the horizontal projections of the spins do NOT in general spread out uniformally in the horizontal plane (i. e. they do not fully decohere in the damping ring). The he. Li. Cal collaboration A. Birch+, J. A. Clarke+, O. B. Malyshev+, D. J. Scott+, B. J. A. Shepherd+ STFC ASTe. C Daresbury Laboratory, Daresbury, Warrington, Cheshire WA 4 4 AD, UK Feynman Diagrams for the second order coherent Breit-Wheeler process. The double lines represent solutions to the Dirac equation in an external field. E. Baynham, T. Bradshaw, A. Brummitt, S. Carr, Y. Ivanyushenkov, A. Lintern, J. Rochford STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire OX 11 0 QX, UK I. R. Bailey+, P. Cooke, J. B. Dainton+, K. Hock+, L. Jenner+, L. Malysheva+, L. Zang+ Future Work v The SLICKTRACK computer code will be extended to include non-linear orbital motion, which will allow a detailed study of spin motion in non-linear elements such as the helical undulator in the ILC positron source and sextupoles in the damping rings. (Current analytical studies predict there will be no appreciable depolarisation of the ILC electron beam in the helical undulator. ) v. The validity of the Equivalent Photon Approximation (EPA) used in CAIN to model the incoherent pair production processes will be investigated, particularly in the case of bremsstrahlung, and the fully polarized cross-sections will be incorporated into the software. v. Second-order coherent pair production processes will be included in the CAIN software. v. Studies of polarized positron production in the positron source will be extended to include details such as electron beam jitter, and the modular design of the helical undulator. v. Investigations into the decoherence of horizontal components of spin vectors in the ILC damping rings will be extended to include injected bunch length effects. v. An ongoing rolling study of spin dynamics in the ILC will be maintained, and results updated periodically as the design of the lattice evolves. Department of Physics, University of Liverpool, Oxford St. , Liverpool, L 69 7 ZE, UK D. P. Barber+ DESY-Hamburg, Notkestraße 85, 22607 Hamburg, Germany G. A. Moortgat-Pick+ Institute of Particle Physics Phenomenology, University of Durham, Durham DH 1 3 LE, UK A. Hartin John Adams Institute, Oxford University Physics, Oxford, OX 1 3 RH, UK. + Cockcroft Institute, Daresbury Laboratory, Daresbury, Warrington, Cheshire WA 4 4 AD, UK Work supported by the Commission of the European Communities under the 6 th Framework Programme “Structuring the European Research Area”, contract number RIDS-011899.
Spin Tracking at the International Linear Collider Overview v. High intensity polarized e- and e+ beams are needed for realising the full physics potential of the ILC. v. Polarized e- source is already in ILC baseline design, and baseline e+ source gives approximately ~30% polarization, upgradeable to ~60%. v. Precision physics requires uncertainty on beam polarization at interaction point ~0. 1%. v. We are developing reliable software tools to optimise the ILC for polarisation delivery as well as luminosity. v. Polarization of an ensemble of particles is defined as v. Currently simulating damping rings, main linac, beam delivery system, bunch-bunch interactions and positron source. L left-handed helicity state, R right-handed helicity state v. We need full cradle-to-grave spin tracking. Sources of depolarisation spin rotators Software Tools (polarized) sources Collimator / Target Capture Optics Physics Process Electrodynamics Standard Model T-BMT (spin spread) Packages SPECTRA, URGENT GEANT 4, FLUKA ASTRA Damping ring Main Linac / BDS T-BMT (spin diffusion) T-BMT Classical spin precession in inhomogeneous external fields: T-BMT equation. Bunch-Bunch Packages SLICKTRACK, (Merlin) SLICKTRACK (Merlin) CAIN 2. 35 (Guinea-Pig) beam-beam interaction Damping Rings Beam-Beam T-BMT Equation in Strong Field Spin precession is described by the Thomas--Bargmann-Michel-Telegdi (T-BMT) equation in terms of the anomalous moment of the electron. In the environment of strong colliding beams however, the usual perturbation theory cannot be applied. Therefore modified expressions for the anomalous magnetic moment in a medium have been derived. These expressions have been evaluated in the “no scattering” case and using the quasiclassical approximation which requires that the change in the momentum due to the strong fields has to be sufficiently slow. It has been checked that even in the strong field environment of the ILC such a quasiclassical approximation can be used and the T-BMT equation can be applied to describe the spin precession sufficiently accurately. After production, the electrons and positrons pass through damping rings containing wiggler magnets which act to radiatively ‘cool’ the beams. Although it expected that in a damping ring that has been well designed and sufficiently well aligned the depolarisation will be negligible, this expectation should be checked since the enhancement of synchrotron radiation by the wigglers has the potential to cause spin depolarisation. In the SLICKTRACK Monte Carlo simulations below, the injected particle bunches are configured to have their spins initially aligned along “n 0” (the solution to the T-BMT equation on the closed orbit), and the damping ring lattice contains realistic magnet misalignments. It can be seen that even close to spin-orbit resonance or with a large injected energy spread the degree of depolarisation after 8000 turns (8 damping times) is negligible. Mean square angular deviation from the equilibrium direction mrad**2 The largest depolarisation effects in the ILC are expected to occur during the beam-beam interactions. The interactions have been simulated using the CAIN software package which evaluates analytically the spin precession as well as the spin-flip Sokolov-Ternov (S-T) effect. Usually the spin precession effect is dominant, but at higher energy the depolarization due to the S-T effect increases. Studies and extensions of the CAIN physics model are presented below. Incoherent Pair Production Coherent Pair Production Turns The mean square angle of tilt away from vertical vs. turns in the OCS 6 ring at 4. 8 Ge. V (close to spin-orbit resonance) with +/- 45 ke. V injected energy spread as expected for ILC electron source. Mean square angular deviation from the equilibrium direction mrad**2 Incoherent pair production processes • Breit-Wheeler ( + → e+ + e-) • Bethe-Heitler (e± + → e± + e+ + e-) • Landau-Lifshitz (e+ + e- → e+ + e- + e+ + e-) • Bremsstrahlung (e+ + e- → e+ + e- + ) dominate over coherent pair production processes at ILC energies. However, the production of background pairs is strongly dependent on the polarization state of the initial photons involved in the process. At present the Breit-Wheeler production cross-section in CAIN is approximated by an expression that only takes into account the circular polarizations of the two initial photons. In the figure on the left a comparison is shown between the CAIN approximation and the full crosssection for each of seven different possible ILC parameter sets. A 10% to 20% reduction in the number of incoherent pairs produced is observed using the full cross-section, whilst there is no discernible change in collision luminosity. Further investigations are ongoing. The coherent production of pairs via the first order interaction between a beamstrahlung photon and the beam field is included already in CAIN. However the second order stimulated Breit-Wheeler process (shown on the right) also takes place in the presence of the bunch fields. The bunch field has the effect of allowing the second order cross-section to reach the mass shell which means that the stimulated Breit. Wheeler cross-section can exceed the first order coherent process cross-section. The second order process is currently being added to CAIN. Stochastic spin diffusion from photon emission: Sokolov-Ternov effect, etc. Interaction Region Physics Process damping beam delivery system rings spin rotators Positron Source Undulator Spin depolarisation mechanisms Turns The mean square angle of tilt away from vertical vs. turns in the OCS 6 ring at 5. 0 Ge. V (nominal operating energy) with +/- 25 Me. V injected energy spread as expected for the ILC positron source. In addition to the above, it has been shown that if the injected spins are not aligned along “n 0” (eg due to a spin rotator misalignment) the horizontal projections of the spins do NOT in general spread out uniformally in the horizontal plane (i. e. they do not fully decohere in the damping ring). The he. Li. Cal collaboration A. Birch+, J. A. Clarke+, O. B. Malyshev+, D. J. Scott+, B. J. A. Shepherd+ STFC ASTe. C Daresbury Laboratory, Daresbury, Warrington, Cheshire WA 4 4 AD, UK Feynman Diagrams for the second order coherent Breit-Wheeler process. The double lines represent solutions to the Dirac equation in an external field. E. Baynham, T. Bradshaw, A. Brummitt, S. Carr, Y. Ivanyushenkov, A. Lintern, J. Rochford STFC Rutherford Appleton Laboratory, Chilton, Didcot, Oxfordshire OX 11 0 QX, UK I. R. Bailey+, P. Cooke, J. B. Dainton+, K. Hock+, L. Jenner+, L. Malysheva+, L. Zang+ Future Work v The SLICKTRACK computer code will be extended to include non-linear orbital motion, which will allow a detailed study of spin motion in non-linear elements such as the helical undulator in the ILC positron source and sextupoles in the damping rings. (Current analytical studies predict there will be no appreciable depolarisation of the ILC electron beam in the helical undulator. ) v. The validity of the Equivalent Photon Approximation (EPA) used in CAIN to model the incoherent pair production processes will be investigated, particularly in the case of bremsstrahlung, and the fully polarized cross-sections will be incorporated into the software. v. Second-order coherent pair production processes will be included in the CAIN software. v. Studies of polarized positron production in the positron source will be extended to include details such as electron beam jitter, and the modular design of the helical undulator. v. Investigations into the decoherence of horizontal components of spin vectors in the ILC damping rings will be extended to include injected bunch length effects. v. An ongoing rolling study of spin dynamics in the ILC will be maintained, and results updated periodically as the design of the lattice evolves. Department of Physics, University of Liverpool, Oxford St. , Liverpool, L 69 7 ZE, UK D. P. Barber+ DESY-Hamburg, Notkestraße 85, 22607 Hamburg, Germany G. A. Moortgat-Pick+ Institute of Particle Physics Phenomenology, University of Durham, Durham DH 1 3 LE, UK A. Hartin John Adams Institute, Oxford University Physics, Oxford, OX 1 3 RH, UK. + Cockcroft Institute, Daresbury Laboratory, Daresbury, Warrington, Cheshire WA 4 4 AD, UK Work supported by the Commission of the European Communities under the 6 th Framework Programme “Structuring the European Research Area”, contract number RIDS-011899.



