Спектральный анализ сигнала Выполнили студенты гр. ПИЭ-517 Калиберда А. О. Лапаева О. П. Журавель А. В. Федореев И. В. Кабаков А. Д. Грибов А. Лекомцева Ю. Е.
Спектральный анализ - это один из методов обработки сигналов, который позволяет охарактеризовать частотный состав измеряемого сигнала. Методы статистики играют важную роль в спектральном анализе, поскольку сигналы, как правило, имеют шумовой или случайный характер. Если бы основные статистические характеристики сигнала были известны точно или же их можно было бы без ошибки определить на конечном интервале этого сигнала, то спектральный анализ представлял бы собой отрасль точной науки. Однако в действительности по одномуединственному отрезку сигнала можно получить только некоторую оценку его спектра. 2
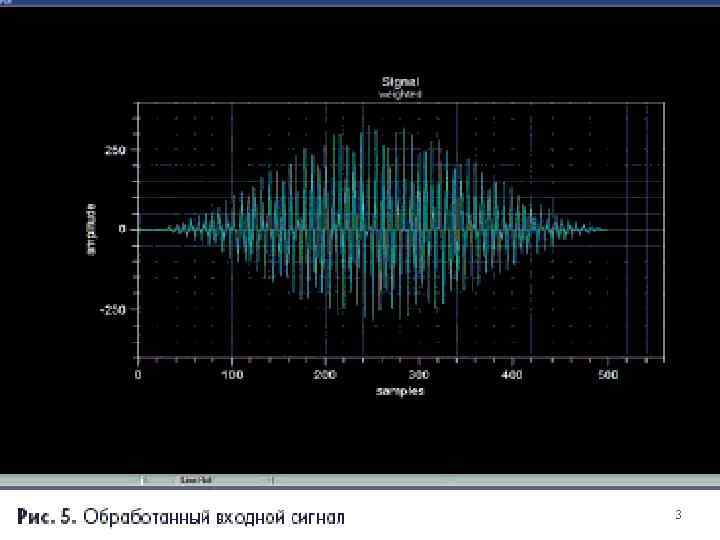
3
При обработке сигналов обычно приходится решать задачи двух типов: 1. Задача обнаружения. При обнаружении нужно дать ответ на вопрос, присутствует ли в данное время на входе некоторый сигнал с априорно известными параметрами. 2. Задача оценивания. Оценивание - это задача измерения значений параметров, описывающих сигнал 4
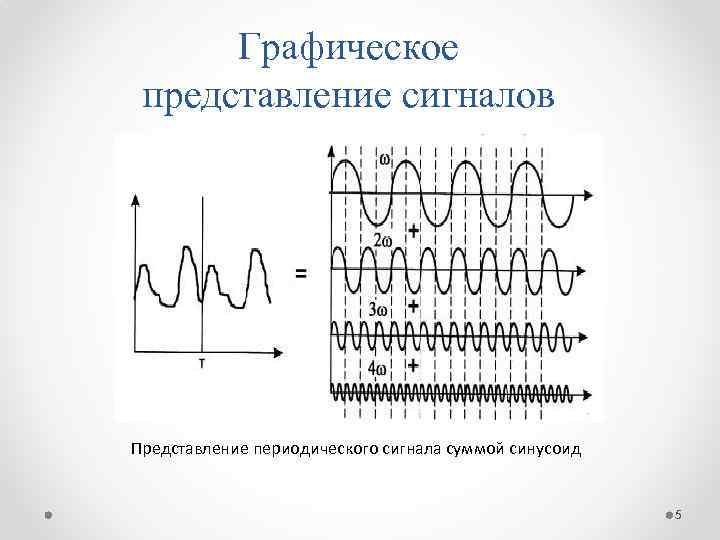
Графическое представление сигналов Представление периодического сигнала суммой синусоид 5
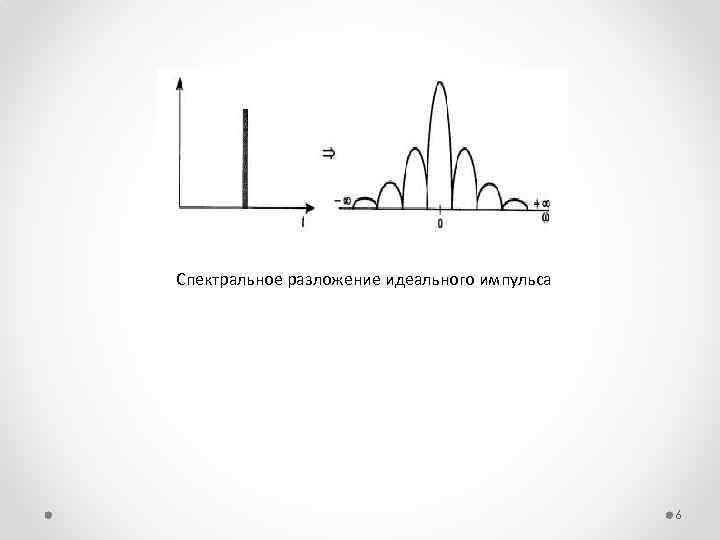
Спектральное разложение идеального импульса 6
Лазерный спектральный анализатор 7
Классический спектр • Всякая периодическая функция (с ограничениями, носящими абстрактный характер) может быть представлена в виде разложения в ряд по тригонометрическим функциям • сk называется амплитудным спектром сигнала, а φk — фазовым спектром. 8
Итоговые формулы, которые являются основными соотношениями теории спектров Формула (1. 2) называется интегралом Фурье в комплексной форме Параметр G(w) выражает не непосредственно амплитуду, а так называемую спектральную плотность. 9
Текущий спектр При анализе спектра мы можем выполнить вычисления лишь от момента начала наблюдения до текущего момента времени t. Текущий спектр- функция не только частоты, но и времени. Мерилом длительности служит число "периодов", которое должно быть намного больше единицы. Спектр процесса (за короткий отрезок времени) однороден, так короткий отрезок процесса - это просто короткий одиночный импульс.
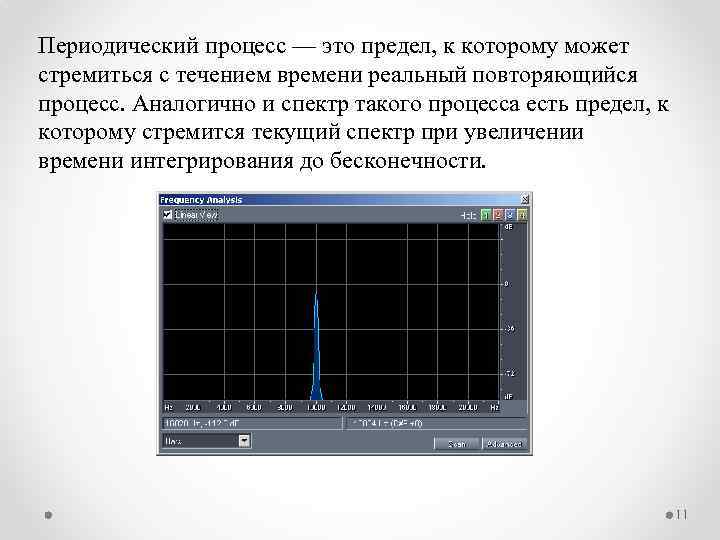
Периодический процесс — это предел, к которому может стремиться с течением времени реальный повторяющийся процесс. Аналогично и спектр такого процесса есть предел, к которому стремится текущий спектр при увеличении времени интегрирования до бесконечности. 11
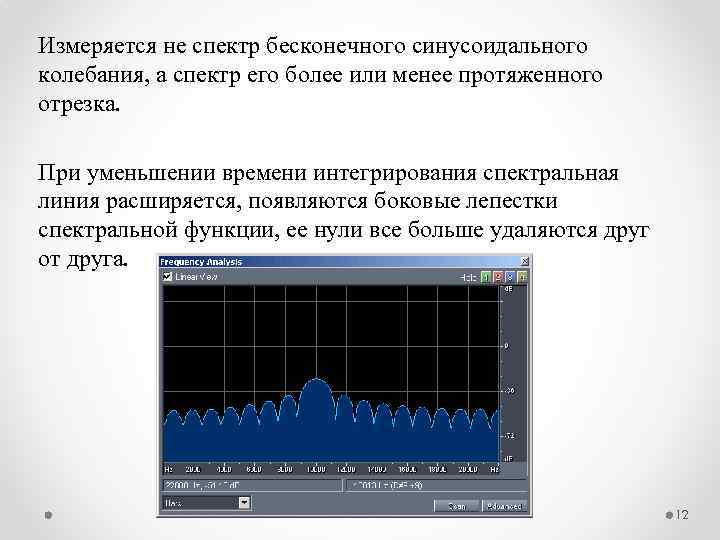
Измеряется не спектр бесконечного синусоидального колебания, а спектр его более или менее протяженного отрезка. При уменьшении времени интегрирования спектральная линия расширяется, появляются боковые лепестки спектральной функции, ее нули все больше удаляются друг от друга. 12
Текущий спектр в большей степени отражает свойства сигналов, проявляющиеся в реальных условиях их генерирования и обработки, нежели спектр, полученный на бесконечном временном интервале. 13
Мгновенный спектр — это спектр короткого отрезка процесса, непосредственно предшествующего данному моменту времени. 14
15
Ряд Фурье Тригонометрическим рядом Фурье функции f называют функциональный ряд вида где
Дифференцирование рядов Фурье Если выполняются следующее условие то разложение в ряд Фурье производной f ' (x) выражается формулой 17
Интегрирование рядов Фурье где x = 0, Следовательно 18
Интегрирование рядов Фурье Рассмотрим функцию Ряд Фурье функции Ф(x) будет определяться выражением где 19
Пример Найти: разложение в ряд Фурье прямоугольной функции с периодом 2π, определенной в интервале [−π, π]: Решение: Вычислим сначала a 0: 20
Определим теперь коэффициенты Фурье при n ≠ 0: Поскольку то можно записать Таким образом, разложение в ряд Фурье для прямоугольной функции имеет вид 21
Можно легко вычислить несколько первых членов разложения. Полагая, например, n = 5, получаем 22
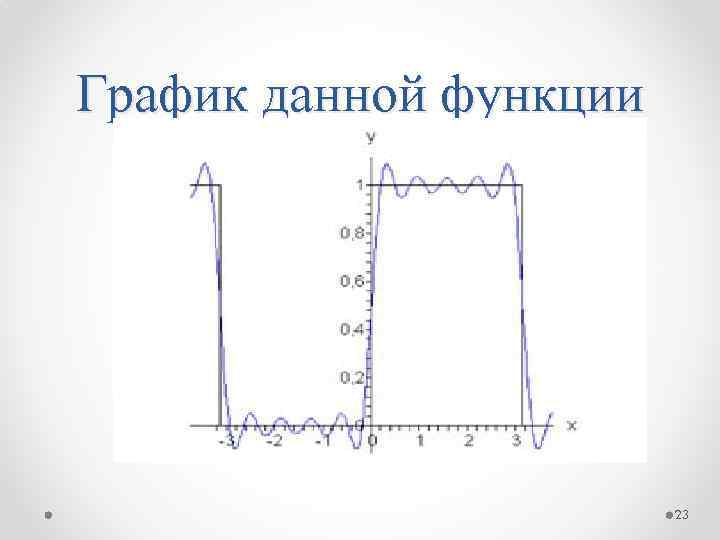
График данной функции 23
Спасибо за внимание! 24
Скачать презентацию Спектральный анализ сигнала Выполнили студенты гр ПИЭ-517 Калиберда
Спектральный анализ сигнала исправ.pptx