СПЕКТРАЛЬНЫЙ АНАЛИЗ БИОМЕДИЦИНСКИХ СИГНАЛОВ А В Литвин

Зарегистрируйтесь, чтобы просмотреть полный документ!

СПЕКТРАЛЬНЫЙ АНАЛИЗ БИОМЕДИЦИНСКИХ СИГНАЛОВ ©А. В. Литвин

Геометрический смысл формулы Эйлера • Формула Эйлера названа в честь Леонарда Эйлера, который её ввёл, и связывает комплексную экспоненту с тригонометрическими функциями. • Формула Эйлера - для любого вещественного числа x выполнено следующее равенство: где e — основание натурального логарифма, • i — мнимая единица.

Производные формулы • Комплексные экспоненты позволяют упростить тригонометрические расчеты. • Благодаря формуле Эйлера появилась тригонометрическая и показательная запись комплексного числа: x = a + ib = | x | (cos φ + isin φ) = | x | eiφ.

Комплексные числа • Ко мпле ксные чи сла (устар. Мнимые числа[2])— числа вида x+iy, где x и y — вещественные числа, i — мнимая единица; i^2=-1. • complex (лат. )— тесно связанный. • Идея о необходимости комплексных чисел возникла в результате формального решения квадратных и кубических уравнений, в которых в формулах для корней уравнения под знаком корня стояло отрицательное число.

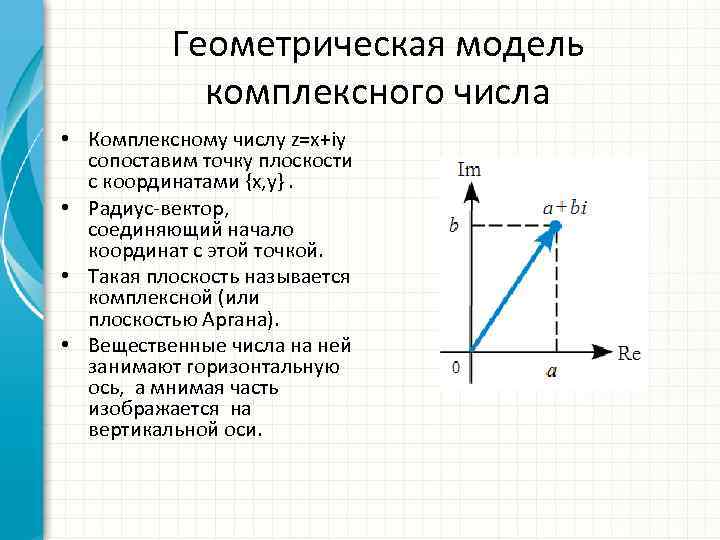
Геометрическая модель комплексного числа • Комплексному числу z=x+iy сопоставим точку плоскости с координатами {x, y}. • Радиус-вектор, соединяющий начало координат с этой точкой. • Такая плоскость называется комплексной (или плоскостью Аргана). • Вещественные числа на ней занимают горизонтальную ось, а мнимая часть изображается на вертикальной оси.

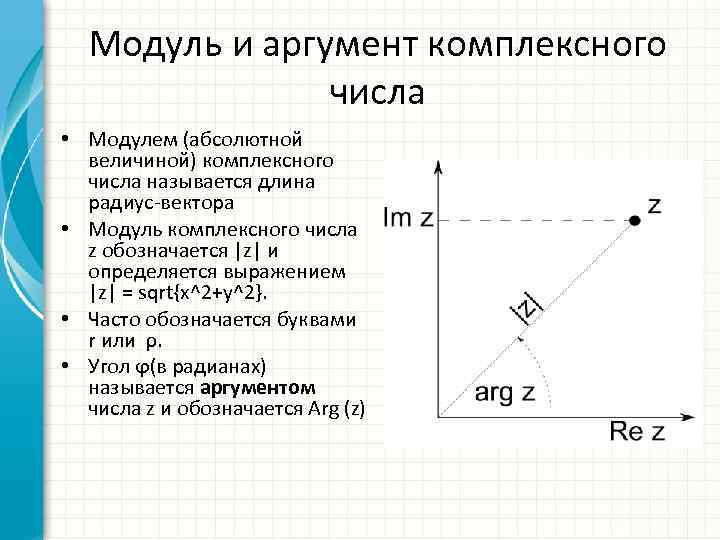
Модуль и аргумент комплексного числа • Модулем (абсолютной величиной) комплексного числа называется длина радиус-вектора • Модуль комплексного числа z обозначается |z| и определяется выражением |z| = sqrt{x^2+y^2}. • Часто обозначается буквами r или ρ. • Угол ϕ(в радианах) называется аргументом числа z и обозначается Arg (z)

Сопряжённые числа • Если комплексное число z=x+iy, то число z*=x-iy называется сопряжённым к z (часто обозначается также z*). На комплексной плоскости сопряжённые числа получаются зеркальным отражением относительно вещественной оси. • Произведение и сумма комплексно-сопряженных чисел есть действительное число: • z* z*=|z|^2. • z + z*=2 Re(z).

Ряд Фурье •

Дискретное преобразование Фурье • Для дискретных данных анализ Фурье выполняется с помощью дискретного преобразования Фурье (ДПФ). • В системе Matlab ДПФ рассчитывается с использованием алгоритмов быстрого преобразования Фурье (БПФ). • Дискретное прямое преобразование Фурье входного вектора x(n) длиной N, является вектором X(k) , который определяется по формуле: где N — количество значений сигнала, измеренных за период; X(k)- выходной вектор, состоящий из N комплексных амплитуд синусоидальных сигналов, слагающих исходный сигнал.

Дискретное преобразование Фурье • В MATLAB расчет характеристик спектра выполняется функцией fft (the fast Fourier transform). Функция fft может быть использована в следующем виде: • Y = fft(X) • Выражение Y = fft(X) возвращает дискретное преобразование Фурье вектора X, рассчитанное по алгоритму быстрого преобразования Фурье. • Если X является матрицей, функция fft определяет преобразование Фурье для каждого столбца матрицы.

Частота дискретизации • Частота дискретизации входного сигнала определяется теормой Котельникова / Найквиста. • Частота регистрации должна быть больше или равна удвоенной частоте процесса. • Частота дискретизации сложного сигнала, состоящего из нескольких гармонических сигналов должна быть равна или быть больше удвоенной наибольшей частоте, составляющей сигнала: • fs ≥ fmax.

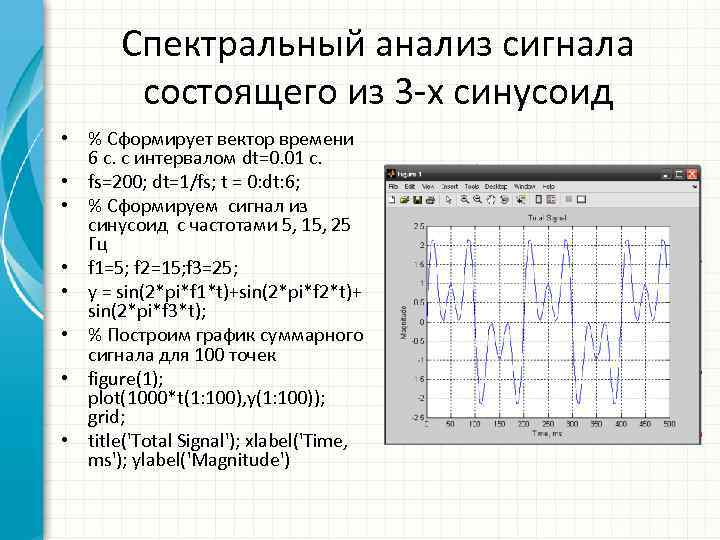
Спектральный анализ сигнала состоящего из 3 -х синусоид • % Сформирует вектор времени 6 с. с интервалом dt=0. 01 с. • fs=200; dt=1/fs; t = 0: dt: 6; • % Сформируем сигнал из синусоид с частотами 5, 15, 25 Гц • f 1=5; f 2=15; f 3=25; • y = sin(2*pi*f 1*t)+sin(2*pi*f 2*t)+ sin(2*pi*f 3*t); • % Построим график суммарного сигнала для 100 точек • figure(1); plot(1000*t(1: 100), y(1: 100)); grid; • title('Total Signal'); xlabel('Time, ms'); ylabel('Magnitude')

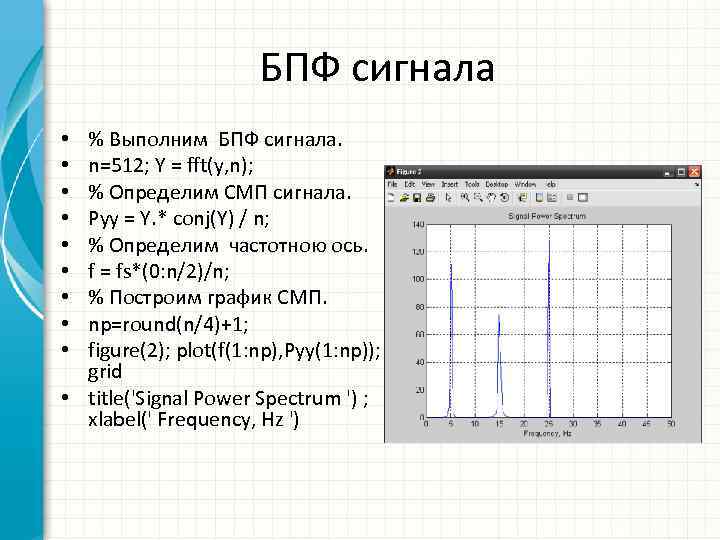
БПФ сигнала % Выполним БПФ сигнала. n=512; Y = fft(y, n); % Определим СМП сигнала. Pyy = Y. * conj(Y) / n; % Определим частотною ось. f = fs*(0: n/2)/n; % Построим график СМП. np=round(n/4)+1; figure(2); plot(f(1: np), Pyy(1: np)); grid • title('Signal Power Spectrum ') ; xlabel(' Frequency, Hz ') • • •

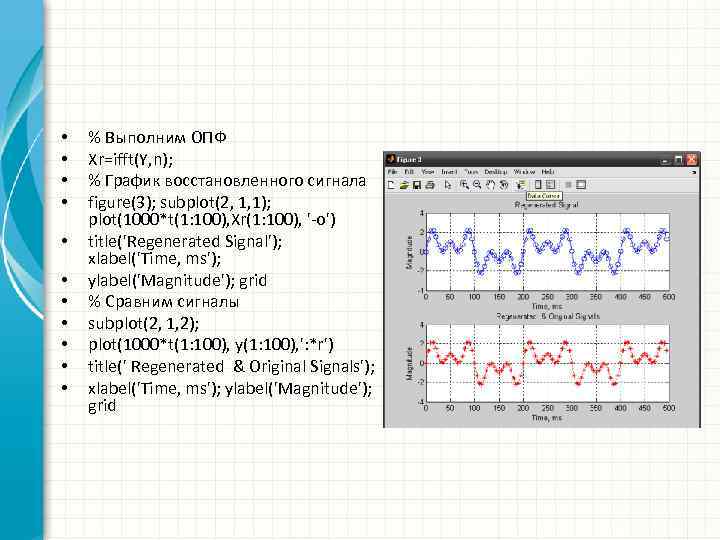
• • • % Выполним ОПФ Xr=ifft(Y, n); % График восстановленного сигнала figure(3); subplot(2, 1, 1); plot(1000*t(1: 100), Xr(1: 100), '-o') title('Regenerated Signal'); xlabel('Time, ms'); ylabel('Magnitude'); grid % Сравним сигналы subplot(2, 1, 2); plot(1000*t(1: 100), y(1: 100), ': *r') title(' Regenerated & Original Signals'); xlabel('Time, ms'); ylabel('Magnitude'); grid

Скачать презентацию СПЕКТРАЛЬНЫЙ АНАЛИЗ БИОМЕДИЦИНСКИХ СИГНАЛОВ А В Литвин

ПрЗ-1 Спектральный анализ БМС.pptx

Количество слайдов: 15