Spectrum Sharing Games of Network Operators and Cognitive

Spectrum Sharing Games of Network Operators and Cognitive Radios Jean-Pierre Hubaux EPFL Work done in collaboration with M. H. Manshaei, M. Felegyhazi, J. Freudiger, and P. Marbach 1

Contents 1. 2. 3. Spectrum allocation and usage Introduction to game theory Spectrum sharing games – – – 4. Network operators • Asymmetric network operators • Border games of cellular operators • Operators in shared spectrum Unlicensed bands • Asymmetric wireless systems • Wi. Fi operators Cognitive radios • Opportunistic spectrum sharing • Auction based spectrum sharing • Multi-Cell OFDM spectrum sharing Conclusion 2

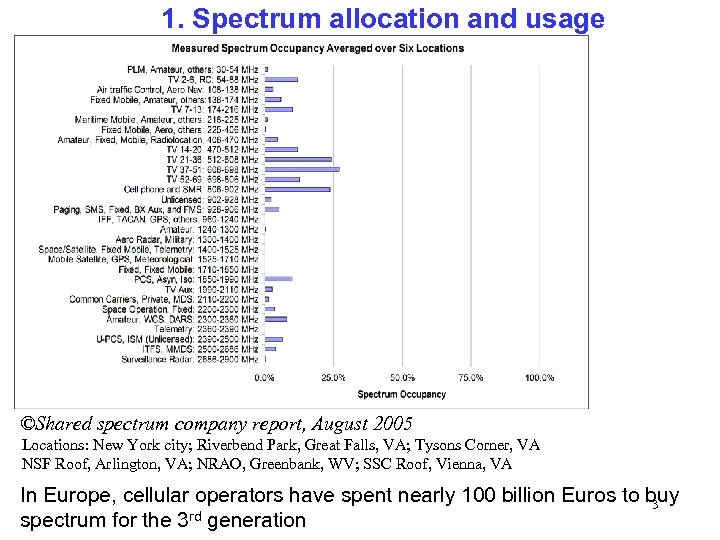1. Spectrum allocation and usage ©Shared spectrum company report, August 2005 Locations: New York city; Riverbend Park, Great Falls, VA; Tysons Corner, VA NSF Roof, Arlington, VA; NRAO, Greenbank, WV; SSC Roof, Vienna, VA In Europe, cellular operators have spent nearly 100 billion Euros to buy 3 rd generation spectrum for the 3

Real-time airwaves auction model • Proposal by Google, inspired by their online advertising auction • Filed to FCC in May 2007 • Would allow commercial operators (including small ones) to bid for access to spectrum controlled by the actual licensee • Supposed to improve spectrum use and create a robust market for innovative digital services 4

2. Brief introduction to Game Theory • Discipline aiming at modeling situations in which actors have to make decisions which have mutual, possibly conflicting, consequences • Classical applications: economics, but also politics and biology • Example: should a company invest in a new plant, or enter a new market, considering that the competition may make similar moves? • Most widespread kind of game: non-cooperative (meaning that the players do not attempt to find an agreement about their possible moves) 5

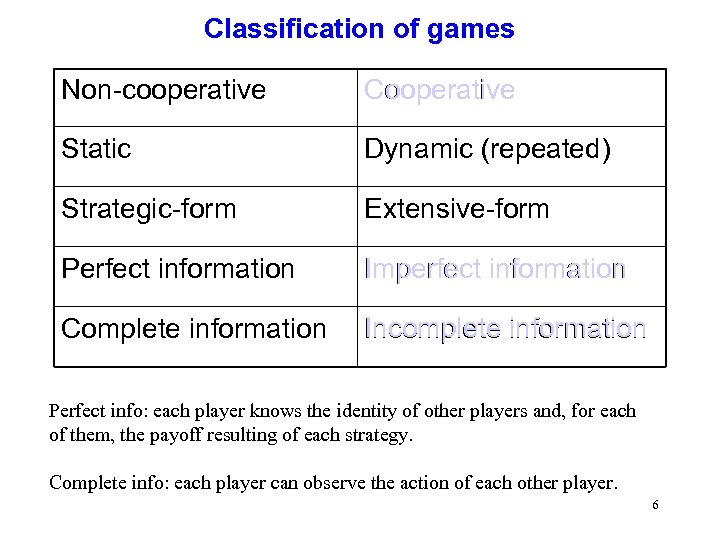Classification of games Non-cooperative Cooperative Static Dynamic (repeated) Strategic-form Extensive-form Perfect information Imperfect information Complete information Incomplete information Perfect info: each player knows the identity of other players and, for each of them, the payoff resulting of each strategy. Complete info: each player can observe the action of each other player. 6

Static (or “single-stage”) games 7

Example 1: The Forwarder’s Dilemma ? Blue Green ? 8

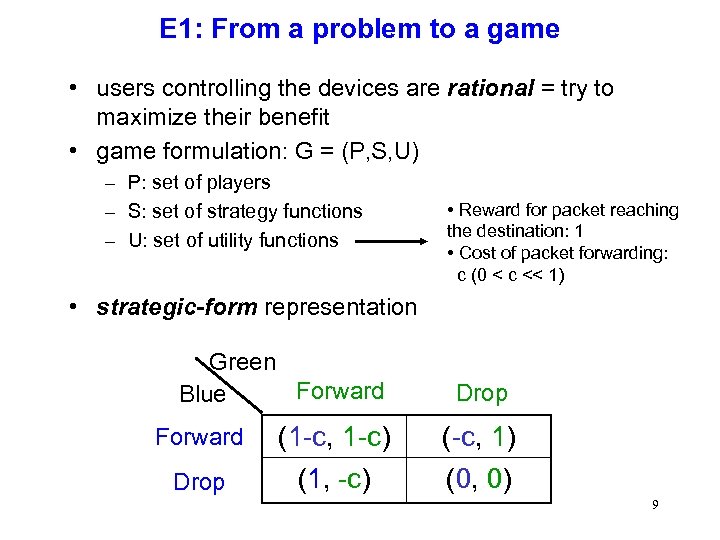E 1: From a problem to a game • users controlling the devices are rational = try to maximize their benefit • game formulation: G = (P, S, U) – P: set of players – S: set of strategy functions – U: set of utility functions • Reward for packet reaching the destination: 1 • Cost of packet forwarding: c (0 < c << 1) • strategic-form representation Green Forward Blue Drop Forward (1 -c, 1 -c) (-c, 1) Drop (1, -c) (0, 0) 9

Solving the Forwarder’s Dilemma (1/2) Strict dominance: strictly best strategy, for any strategy of the other player(s) Strategy strictly dominates if utility function of player i where: strategies of all players except player i In Example 1, strategy Drop strictly dominates strategy Forward Green Forward Blue Drop Forward (1 -c, 1 -c) (-c, 1) Drop (1, -c) (0, 0) 10

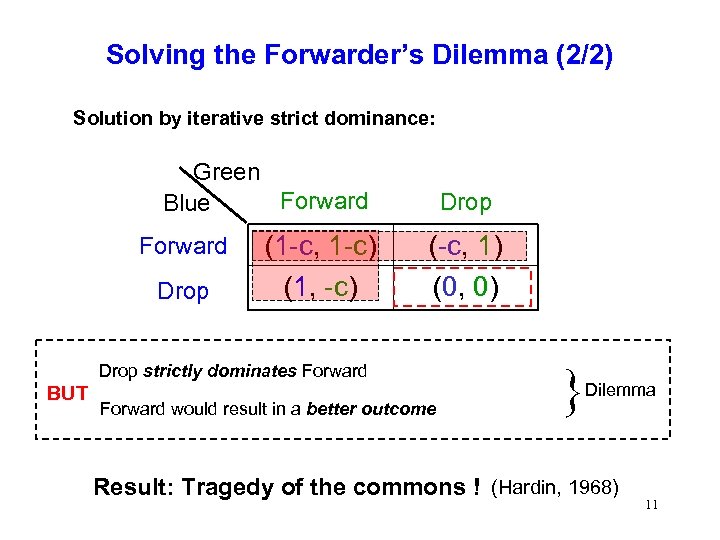Solving the Forwarder’s Dilemma (2/2) Solution by iterative strict dominance: Green Forward Blue Forward Drop (1 -c, 1 -c) (1, -c) Drop (-c, 1) (0, 0) Drop strictly dominates Forward BUT Forward would result in a better outcome } Dilemma Result: Tragedy of the commons ! (Hardin, 1968) 11

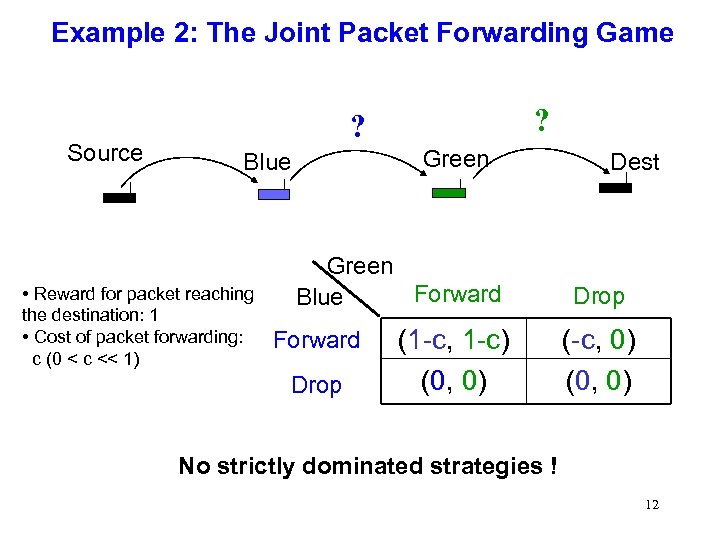Example 2: The Joint Packet Forwarding Game Source ? ? Green Blue • Reward for packet reaching the destination: 1 • Cost of packet forwarding: c (0 < c << 1) Green Forward Blue Forward Drop (1 -c, 1 -c) (0, 0) Dest Drop (-c, 0) (0, 0) No strictly dominated strategies ! 12

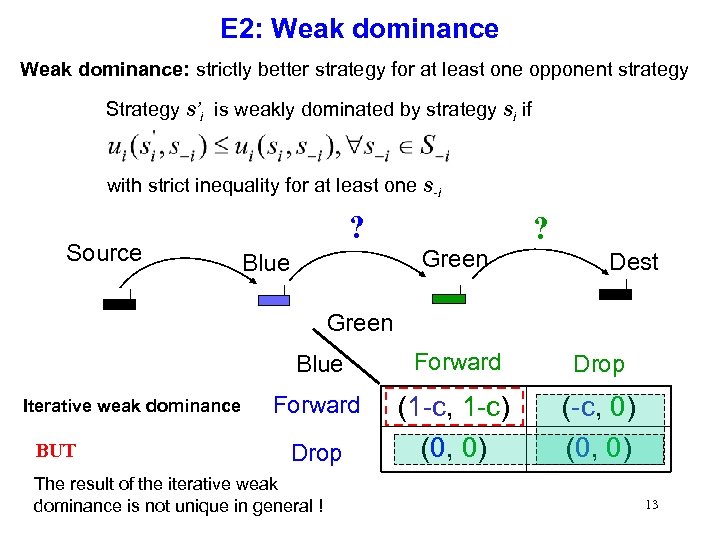E 2: Weak dominance: strictly better strategy for at least one opponent strategy Strategy s’i is weakly dominated by strategy si if with strict inequality for at least one s-i Source ? ? Green Blue Dest Green Blue Iterative weak dominance BUT Forward Drop Forward (1 -c, 1 -c) (0, 0) (-c, 0) (0, 0) Drop The result of the iterative weak dominance is not unique in general ! 13

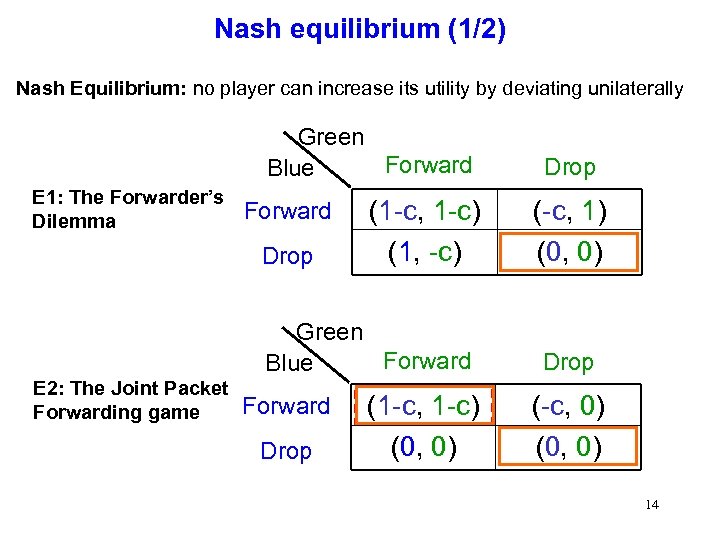Nash equilibrium (1/2) Nash Equilibrium: no player can increase its utility by deviating unilaterally Green Forward Blue E 1: The Forwarder’s Dilemma Forward Drop (1 -c, 1 -c) (1, -c) Green Forward Blue E 2: The Joint Packet Forwarding game Forward Drop (1 -c, 1 -c) (0, 0) Drop (-c, 1) (0, 0) Drop (-c, 0) (0, 0) 14

Nash equilibrium (2/2) Strategy profile s* constitutes a Nash equilibrium if, for each player i, where: utility function of player i strategy of player i The best response of player i to the profile of strategies s-i is a strategy si such that: Nash Equilibrium = Mutual best responses Caution! Many games have more than one Nash equilibrium 15

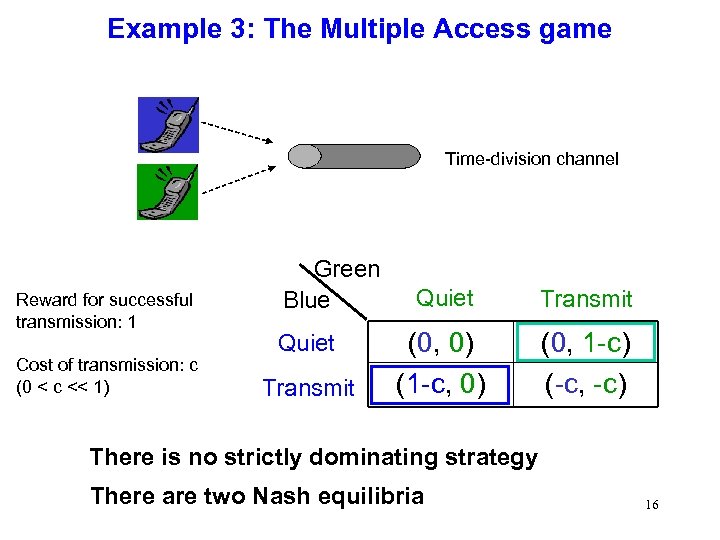Example 3: The Multiple Access game Time-division channel Reward for successful transmission: 1 Cost of transmission: c (0 < c << 1) Green Blue Quiet Transmit (0, 0) (1 -c, 0) (0, 1 -c) (-c, -c) There is no strictly dominating strategy There are two Nash equilibria 16

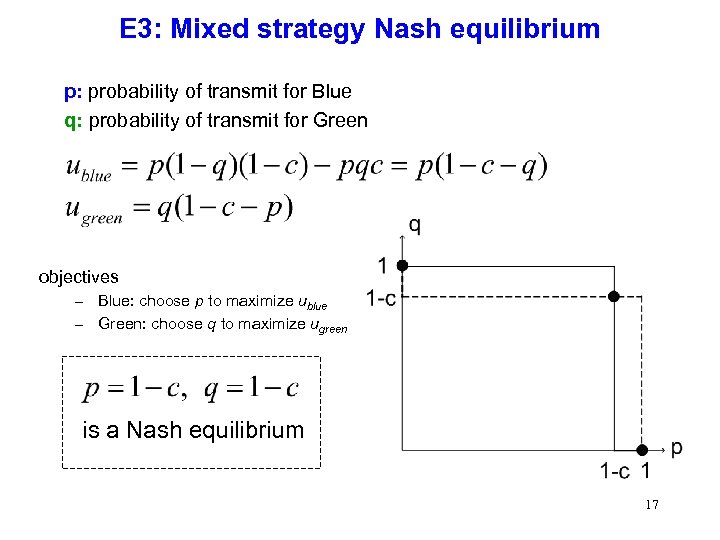E 3: Mixed strategy Nash equilibrium p: probability of transmit for Blue q: probability of transmit for Green objectives – Blue: choose p to maximize ublue – Green: choose q to maximize ugreen is a Nash equilibrium 17

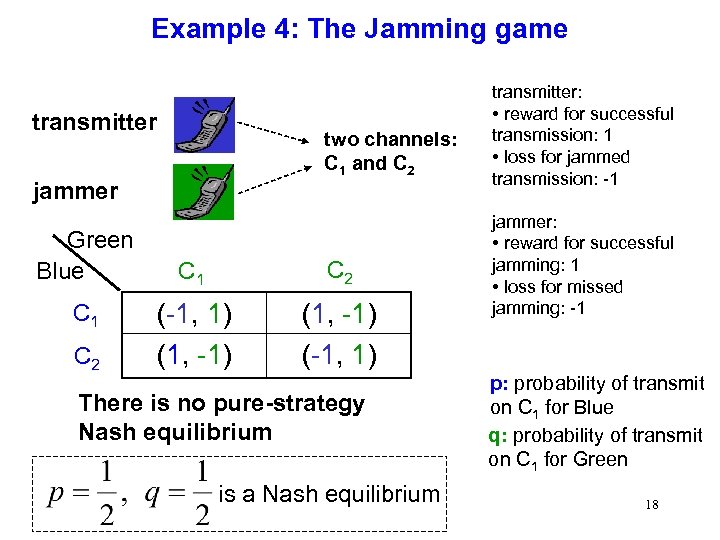Example 4: The Jamming game transmitter two channels: C 1 and C 2 jammer Green Blue C 1 C 2 (-1, 1) (1, -1) (-1, 1) There is no pure-strategy Nash equilibrium is a Nash equilibrium transmitter: • reward for successful transmission: 1 • loss for jammed transmission: -1 jammer: • reward for successful jamming: 1 • loss for missed jamming: -1 p: probability of transmit on C 1 for Blue q: probability of transmit on C 1 for Green 18

Theorem by Nash, 1950 Theorem: Every finite strategic-form game has a mixed-strategy Nash equilibrium. 19

Efficiency of Nash equilibria Green Forward Blue E 2: The Joint Packet Forwarding game Forward Drop (1 -c, 1 -c) (0, 0) Drop (-c, 0) (0, 0) How to choose between several Nash equilibria ? Pareto-optimality: A strategy profile is Pareto-optimal if it is not possible to increase the payoff of any player without decreasing the payoff of another player. 20

How to study Nash equilibria ? Properties of Nash equilibria to investigate: • • existence uniqueness efficiency (Pareto-optimality) emergence (dynamic games, agreements) 21

Repeated games 22

Repeated games • repeated interaction between the players (in stages) • move: decision in one interaction • strategy: defines how to choose the next move, given the previous moves • history: the ordered set of moves in previous stages – most prominent games are history-1 games (players consider only the previous stage) • initial move: the first move with no history • finite-horizon vs. infinite-horizon games • stages denoted by t (or k) 23

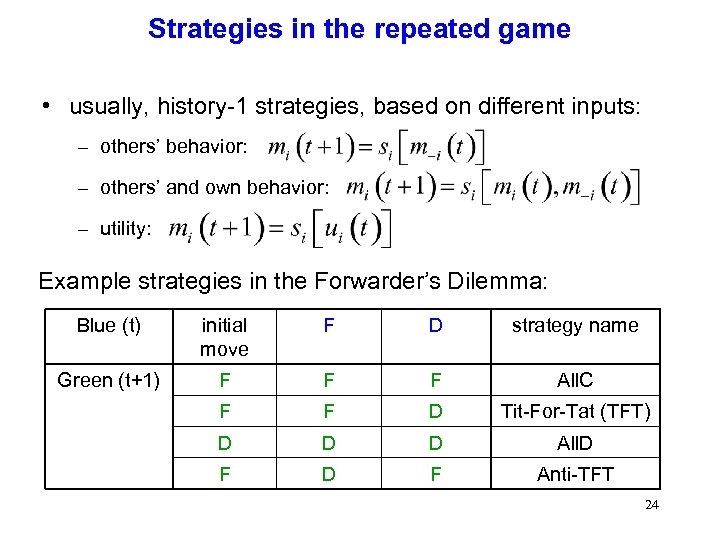Strategies in the repeated game • usually, history-1 strategies, based on different inputs: – others’ behavior: – others’ and own behavior: – utility: Example strategies in the Forwarder’s Dilemma: Blue (t) initial move F D strategy name Green (t+1) F F F All. C F F D Tit-For-Tat (TFT) D D D All. D F Anti-TFT 24

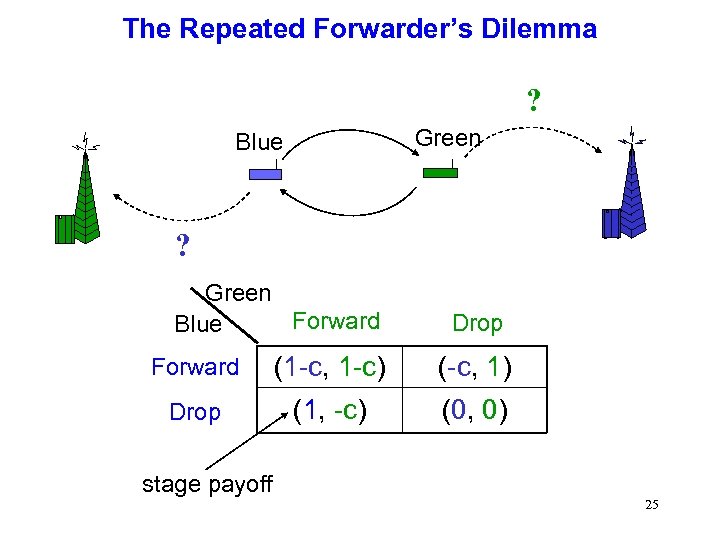The Repeated Forwarder’s Dilemma ? Green Blue ? Green Forward Blue Drop Forward (1 -c, 1 -c) (-c, 1) Drop (1, -c) (0, 0) stage payoff 25

Analysis of the Repeated Forwarder’s Dilemma infinite game with discounting: Blue strategy Green strategy Blue utility Green utility All. D 0 0 All. D TFT 1 -c All. D All. C 1/(1 -ω) -c/(1 -ω) All. C (1 -c)/(1 -ω) All. C TFT (1 -c)/(1 -ω) 26

Conclusion on game theory • Game theory can help modeling greedy behavior in wireless networks • Discipline still in its infancy • Alternative solutions – Ignore the problem – Build protocols in tamper-resistant hardware 27

http: //secowinet. epfl. ch For the tutorial on game theory: 28 M. Felegyhazi and J. -P. Hubaux, Game Theory in Wireless Networks: A Tutorial Technical report – 2006 [LCA-REPORT-2006 -002]

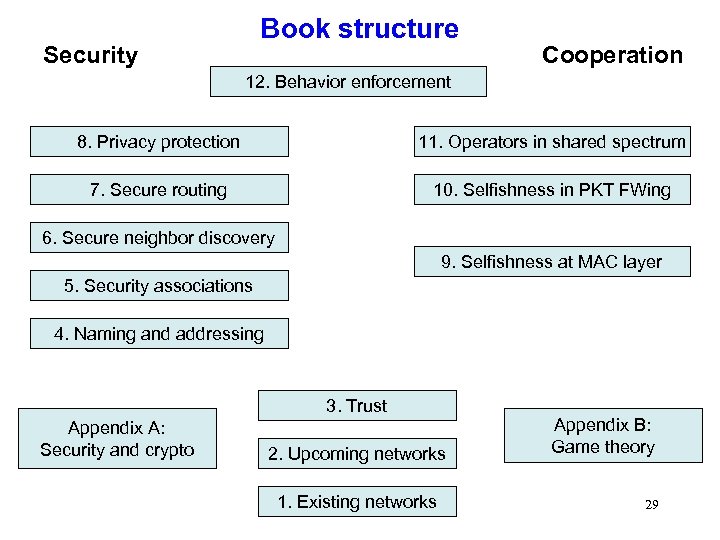Book structure Security Cooperation 12. Behavior enforcement 8. Privacy protection 11. Operators in shared spectrum 7. Secure routing 10. Selfishness in PKT FWing 6. Secure neighbor discovery 9. Selfishness at MAC layer 5. Security associations 4. Naming and addressing 3. Trust Appendix A: Security and crypto 2. Upcoming networks 1. Existing networks Appendix B: Game theory 29

Who is malicious? Who is selfish? Harm everyone: viruses, … Selective harm: Do. S, … Big brother Spammer Cyber-gangster: phishing attacks, trojan horses, … Greedy operator Selfish mobile station There is no watertight boundary between malice and selfishness Both security and game theory approaches can be useful 30

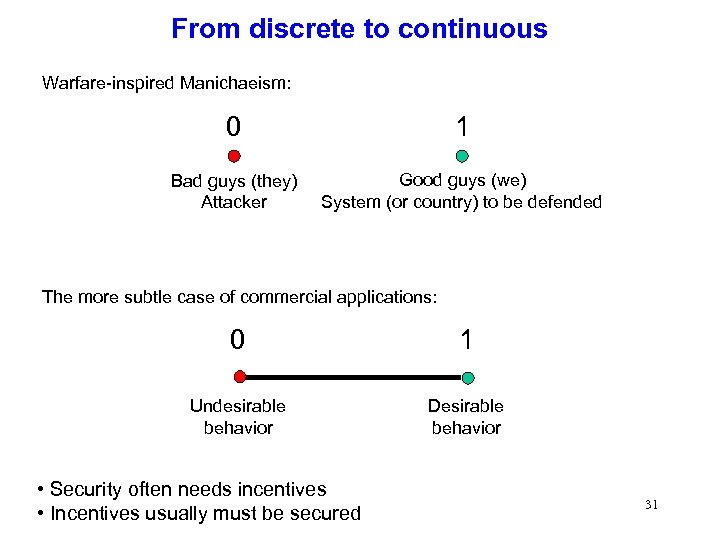From discrete to continuous Warfare-inspired Manichaeism: 0 1 Bad guys (they) Attacker Good guys (we) System (or country) to be defended The more subtle case of commercial applications: 0 1 Undesirable behavior Desirable behavior • Security often needs incentives • Incentives usually must be secured 31

Another book: Cognitive Wireless Networks: Concepts, Methodologies and Visions - Inspiring the Age of Enlightenment of Wireless Communications – Edited by Frank H. P. Fitzek and Marcos D. Katz Part I: Introductory Chapter Part II: Cooperative Networks: Social, Operational and Communicational Aspects Part III: Cognitive Networks Part IV: Marrying Cooperation and Cognition in Wireless Networks Part V: Methodologies and Tools Part VI: Visions, Prospects and Emerging Technologies 32

List of Contributors Aachen University, Germany AIST, Japan Budapest University of Technology and Economics, Hungary Create-NET, Italy Do. Co. Mo Euro-Labs, Germany EPFL, Switzerland Harvard University, USA Konica Italia, Italy KTH, Sweden MIT, USA Motorola Labs, France Oxford University, UK Stevens Institute of Technology, USA Technical University of Catalonia, Spain Technical University of Denmark, Denmark Universität Duisburg Essen, Germany Universität Karlsruhe, Germany University of Aalborg, Denmark University of Bologna, Italy University of California at Berkeley, USA University of California, San Diego, USA University of Dresden, Germany University of Paderborn, Germany University of Padova, Italy University of Piraeus, Greece VTT, Finland WINLAB and Rutgers University, USA 33

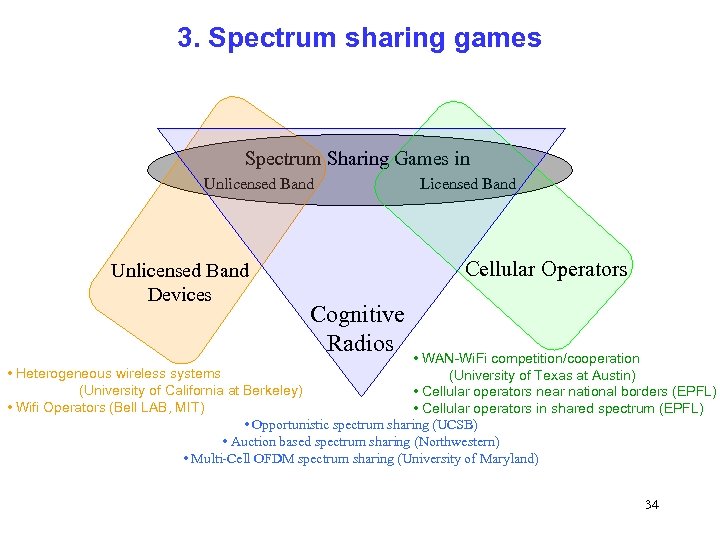3. Spectrum sharing games Spectrum Sharing Games in Unlicensed Band Licensed Band Unlicensed Band Devices Cellular Operators Cognitive Radios • WAN-Wi. Fi competition/cooperation • Heterogeneous wireless systems (University of Texas at Austin) (University of California at Berkeley) • Cellular operators near national borders (EPFL) • Wifi Operators (Bell LAB, MIT) • Cellular operators in shared spectrum (EPFL) • Opportunistic spectrum sharing (UCSB) • Auction based spectrum sharing (Northwestern) • Multi-Cell OFDM spectrum sharing (University of Maryland) 34

3. 1 Spectrum Sharing Games of Network Operators 1. 2. 3. A. Zemlianov and G. de Veciana, “Cooperation and Decision Making in Wireless Multi-provider Setting, ” INFOCOM 2005 M. Felegyhazi et al. , “Border Games in Cellular Networks, ” INFOCOM 2007 M. Felegyhazi and J. -P. Hubaux, “Wireless Operators in a Shared Spectrum, ” INFOCOM 2006 35

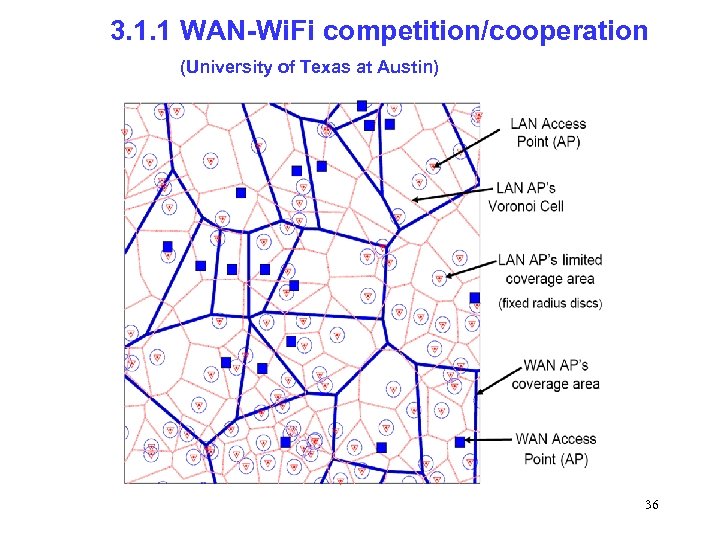3. 1. 1 WAN-Wi. Fi competition/cooperation (University of Texas at Austin) 36

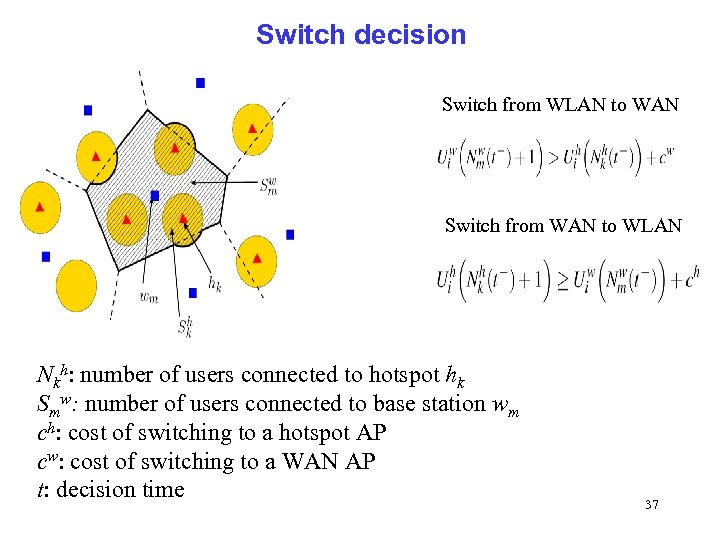Switch decision Switch from WLAN to WAN Switch from WAN to WLAN Nkh: number of users connected to hotspot hk Smw: number of users connected to base station wm ch: cost of switching to a hotspot AP cw: cost of switching to a WAN AP t: decision time 37

Results • • Given any initial configuration of agents’ choices, the system converges to an equilibrium configuration as t ∞ This equilibrium is not necessarily unique The class of payoff functions that are congestion dependent provide much better performance to users on average than the simple proximity-based decision strategy The results can notably help operators with both wireless WAN infrastructure (e. g. , Wi. MAX) and a set of Wi. Fi hotspots to optimize their network 38

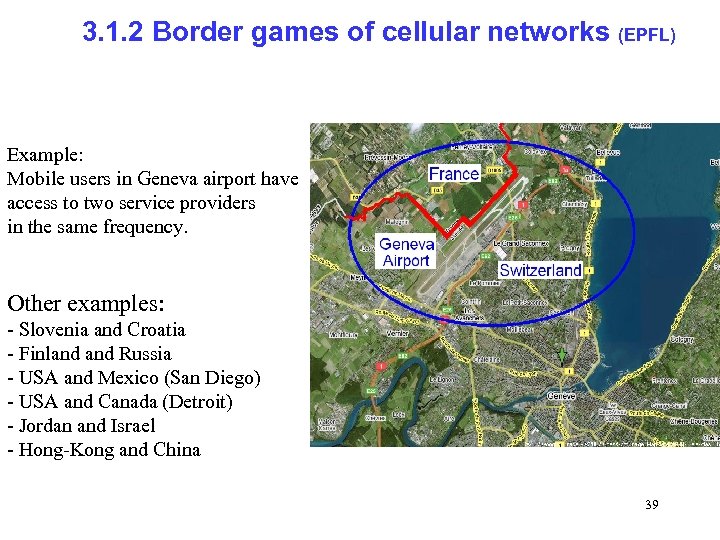3. 1. 2 Border games of cellular networks (EPFL) Example: Mobile users in Geneva airport have access to two service providers in the same frequency. Other examples: - Slovenia and Croatia - Finland Russia - USA and Mexico (San Diego) - USA and Canada (Detroit) - Jordan and Israel - Hong-Kong and China 39

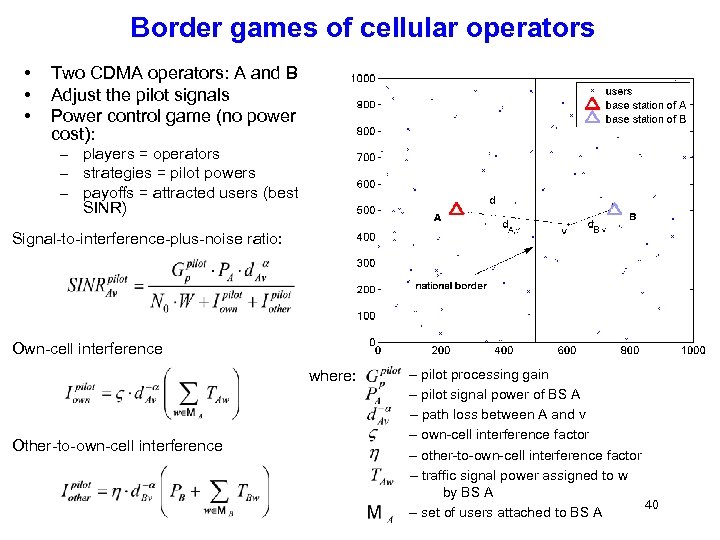Border games of cellular operators • • • Two CDMA operators: A and B Adjust the pilot signals Power control game (no power cost): – players = operators – strategies = pilot powers – payoffs = attracted users (best SINR) Signal-to-interference-plus-noise ratio: Own-cell interference where: Other-to-own-cell interference – pilot processing gain – pilot signal power of BS A – path loss between A and v – own-cell interference factor – other-to-own-cell interference factor – traffic signal power assigned to w by BS A 40 – set of users attached to BS A

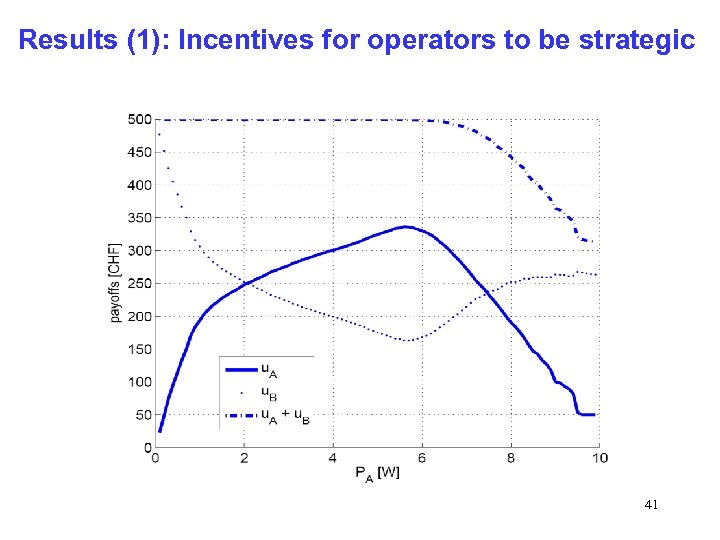Results (1): Incentives for operators to be strategic 41

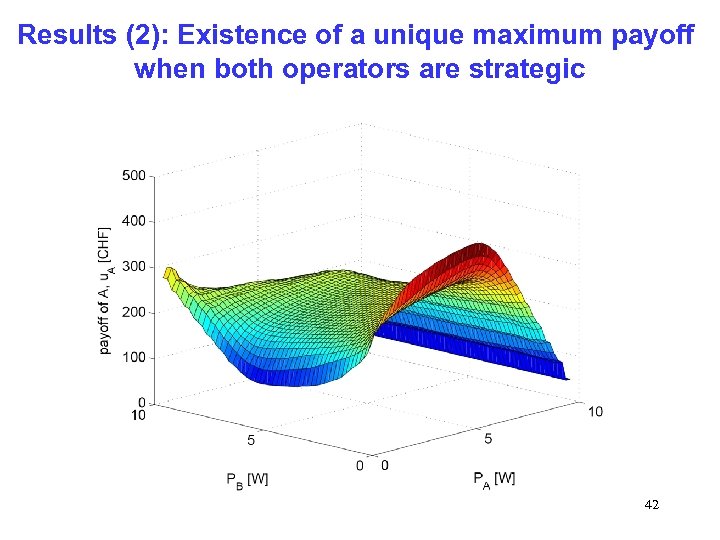Results (2): Existence of a unique maximum payoff when both operators are strategic 42

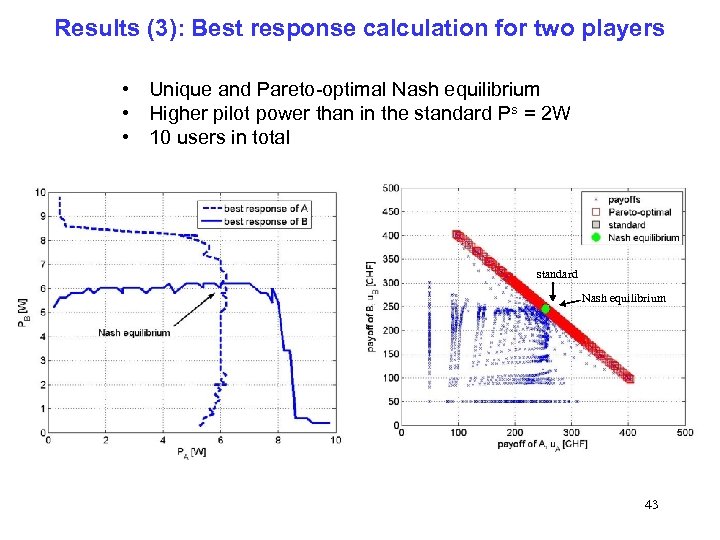Results (3): Best response calculation for two players • Unique and Pareto-optimal Nash equilibrium • Higher pilot power than in the standard Ps = 2 W • 10 users in total standard Nash equilibrium 43

Other results 1. Price of anarchy and price of conformance to evaluate NE 2. Extend payoff function to consider the cost of high pilot power 3. leads to a Prisoner’s dilemma situation U – fair payoff (half of the users) D – payoff difference by selfish behavior C* - cost for higher pilot power 44

3. 1. 3 Operators in a shared spectrum (EPFL) • • • two operators: A and B set of base stations: BA and BB base stations are placed on the vertices of a grid each base station of A has the same radio range r. A (relaxed later), same for B base stations emit pilot signals on the same channel, with the radio ranges: r. A, r. B full coverage by combination of the two operator’s coverage maximum power limit PMAX → RMAX if • devices have omnidirectional antennas • • • 45

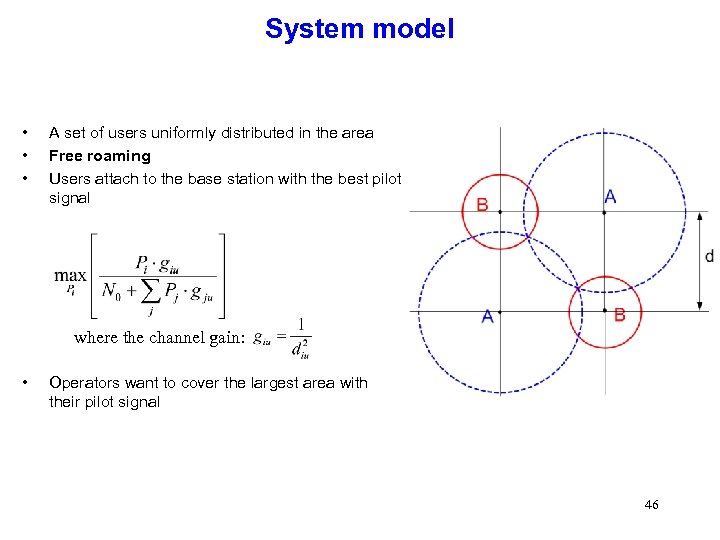System model • • • A set of users uniformly distributed in the area Free roaming Users attach to the base station with the best pilot signal where the channel gain: • Operators want to cover the largest area with their pilot signal 46

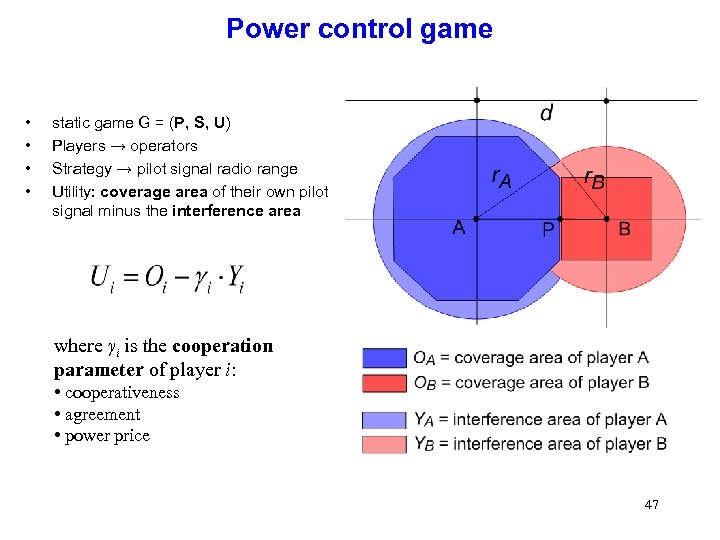Power control game • • static game G = (P, S, U) Players → operators Strategy → pilot signal radio range Utility: coverage area of their own pilot signal minus the interference area where γi is the cooperation parameter of player i: • cooperativeness • agreement • power price 47

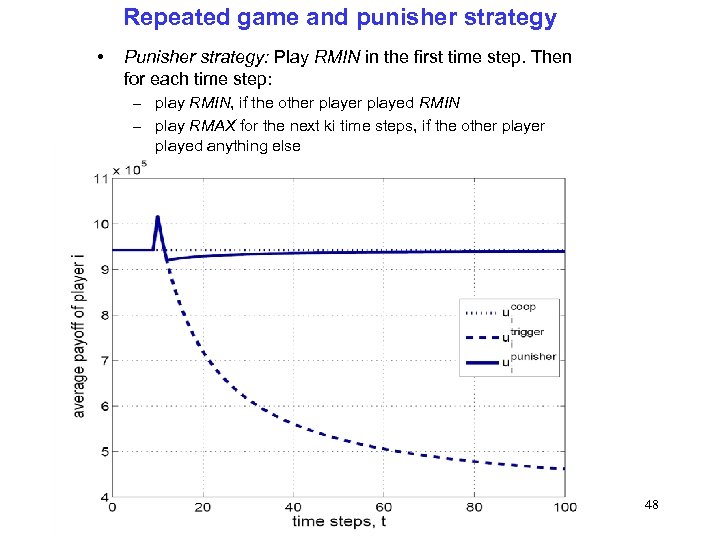Repeated game and punisher strategy • Punisher strategy: Play RMIN in the first time step. Then for each time step: – play RMIN, if the other played RMIN – play RMAX for the next ki time steps, if the other played anything else 48

What is the right cooperation model ? • Non-cooperative games: no trust and no agreement between players • Cooperative games: players talk to each other and try to find an agreement • Cooperation is often assumed at the physical layer (e. g. for beamforming) • Non-cooperative behavior is often (but not always) assumed at the MAC, network, and transport layers 49

A glimpse at IEEE JSAC • Cooperative Communications and Networking – Vol. 25 (2007), issue 2 • Adaptive, Spectrum Agile and Cognitive Wireless Networks – Vol. 25 (2007), issue 3 • Non-Cooperative Behavior in Networking – to appear in Q 3 2007 • Game Theory in Communication Systems – submission due date: August 1, 2007 50

Panel at Mobicom 2007 (Montreal, September 13) Chimpanzee www. ncbi. nlm. nih. gov Bonobo www. bio. davidson. edu Bonobos Vs Chimps: Cooperative and Non-Cooperative Behavior in Wireless Networks Panelists: Jean-Pierre Hubaux, EPFL (organizer and moderator) Ramesh Johari, Stanford University P. R. Kumar, UIUC Joseph Mitola, MITRE Corp. Heather Zheng, UCSB 51

Conclusion • Potential of the area fuelled by: – The emergence of cognitive radios – The willingness to revisit the way spectrum is allocated – The rise of Wi. Fi community networks • Limitations of game theory modeling for wireless networks – Information for the players: games are in reality of incomplete and imperfect information – Expression of payoffs (benefits and costs) – Cooperative Vs non-cooperative games – Reputation of players http: //winet-coop. epfl. ch 52