Спецкурс Microsoft Excel в профильном обучении Раздел 9

Спецкурс «Microsoft Excel в профильном обучении» Раздел 9 “Основы статистического анализа”

Независимо от того, в какой отрасли знания получены числовые данные, они обладают определенными свойствами, для выявления которых может потребоваться особого рода научный метод обработки. Последний известен как статистический метод или, короче, статистика. Дж. Юл. М. Кендал

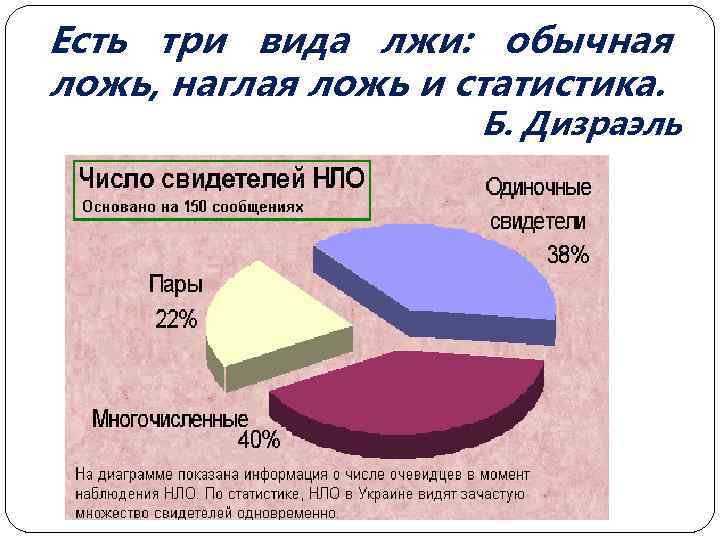
Есть три вида лжи: обычная ложь, наглая ложь и статистика. Б. Дизраэль

План задачи математической статистики; понятие выборки и генеральной совокупности; статистические характеристики выборки; статистические функции Население процессора и их табличного мира на 03 -04 -2014 7 162 267 439 Текущее население использование. 3 612 164 031 Текущее мужское население (50. 4%) 3 550 103 408 Текущее женское население (49. 6%)

Основные понятия математической статистики Математическая статистика – раздел математики, посвященный методам сбора, анализа и обработки статистических данных в научных или практических целях. Применяется там, где исследуются закономерности, присущие крупным совокупностям объектов: в экономике, социологии, серийном производстве и т. д.

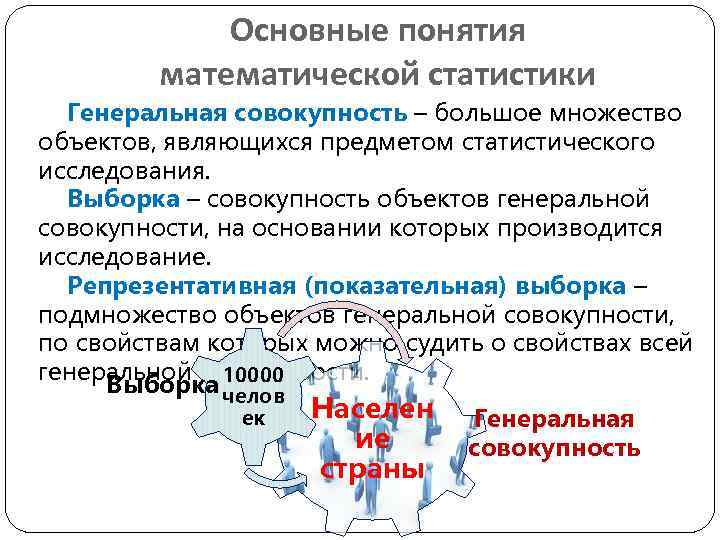
Основные понятия математической статистики Генеральная совокупность – большое множество объектов, являющихся предметом статистического исследования. Выборка – совокупность объектов генеральной совокупности, на основании которых производится исследование. Репрезентативная (показательная) выборка – подмножество объектов генеральной совокупности, по свойствам которых можно судить о свойствах всей генеральной совокупности. 10000 Выборка челов Населен Генеральная ек ие совокупность страны

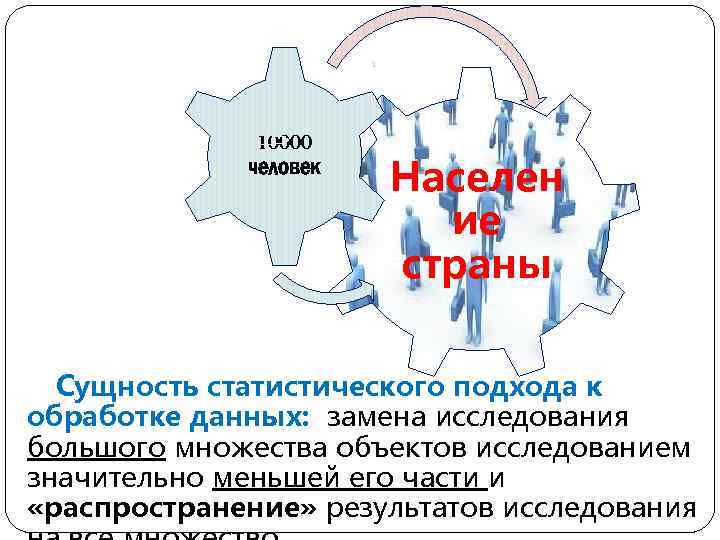
10000 человек Населен ие страны Сущность статистического подхода к обработке данных: замена исследования большого множества объектов исследованием значительно меньшей его части и «распространение» результатов исследования

Статистическое исследование состоит из трех этапов Статистическое наблюдение, сбор данных. Обработка, группировка данных, представление в удобной форме. Анализ статистической информации, выводы, рекомендации. Цель: установление закономерностей, присущих генеральной совокупности.

Этапы статистического исследования 1. На первом этапе формируют статистическую выборку. Ее составляют по результатам: Øопроса групп людей; Øнаблюдения за природными явлениями; Øпроведения серии экспериментов…

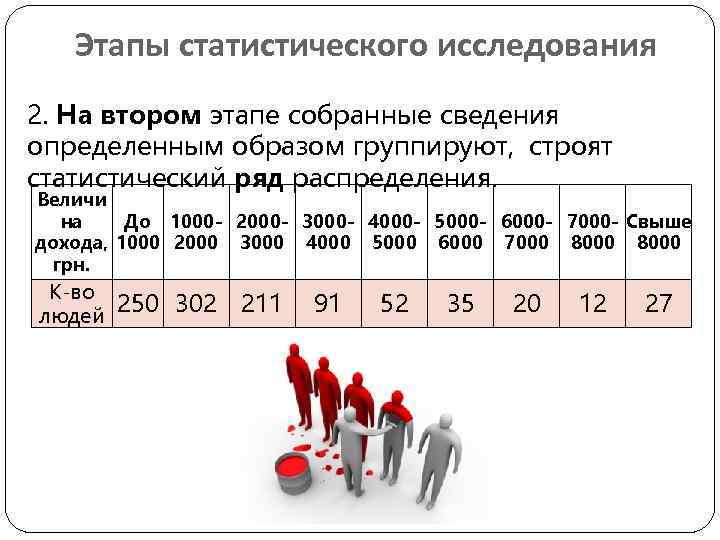
Этапы статистического исследования 2. На втором этапе собранные сведения определенным образом группируют, строят статистический ряд распределения. Величи на До 1000 - 2000 - 3000 - 4000 - 5000 - 6000 - 7000 - Свыше дохода, 1000 2000 3000 4000 5000 6000 7000 8000 грн. К-во людей 250 302 211 91 52 35 20 12 27

Этапы статистического исследования 3. На третьем этапе вычисляются обобщающие показатели и проводится анализ статистической информации.

Основные статистические характеристики выборки В математической статистике изучают числовые характеристики выборок, которые обобщают объекты выборки по определенному признаку. Характеристики выборки из 100 учеников Статистические: набор значений Обобщающие: определенного параметра средняя выбранных объектов успеваемость, (набор годовых оценок максимальный учащихся по математике). рост ученика. Каждый элемент выборки в этом случае называют

Определение статистических показателей выборки Основные числовые характеристики: Среднее значение. Медиана. Мода. Стандартное отклонение, асимметрия. Вариационный размах (показатели вариации).

Показатели центра Позволяют найти более типичное, центральное значение для всей выборки Мода — элемент выборки, который встречается наиболее часто, если таковых несколько, выборка имеет несколько мод. 1) Если все значения в группе встречаются одинаково часто, то мода отсутствует: (1, 1, 2, 2, 13). 2) Если два соседних значения имеют одинаковые частоты и они больше частоты любого другого значения, мода есть среднее этих двух значений: (1, 2, 2, 5, 5, 5, 6, 6, 6, 9, 9, 10) мода равна 5, 5. 3) Если два несмежных значения в группе имеют равные частоты и они больше частот любого другого значения, то существуют две моды. (1, 4, 4, 4, 7, 7, 9, 9, 9, 10).

Показатели центра Среднее значение выборки х — среднее арифметическое всех вариантов выборки: п — объем выборки (количество вариантов в ней); х1 , х2, . . . , хп — все варианты выборки. Сложить и разделить на количество

Показатели центра Медиана выборки — число, являющееся серединой выборки: половина вариантов имеют значения, большие медианы, а половина — меньшие. 1) (1, 3, 5, 8, 11, 15, 20) медиана 8. 2) (1, 3, 5, 8, 11, 15) медиана 6, 5.

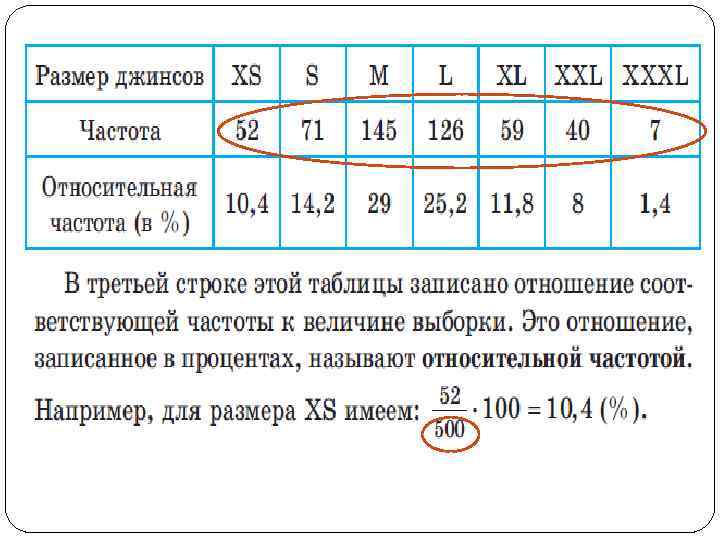
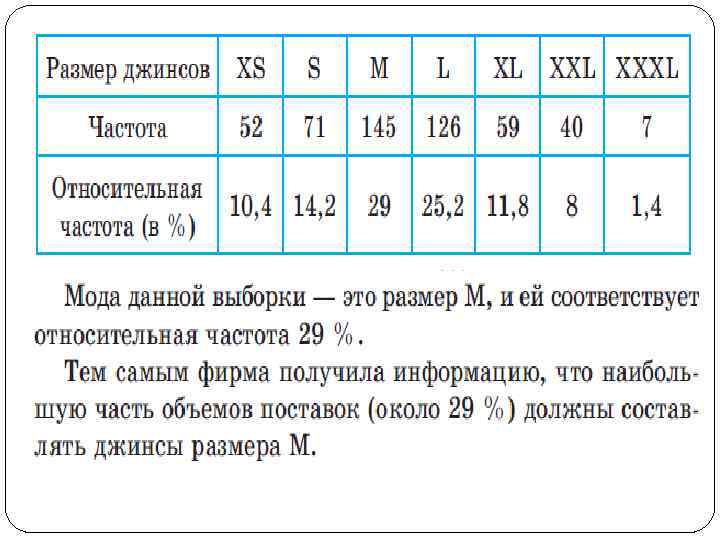
Показатели вариации Позволяют оценить, насколько выборка сплотилась вокруг центрального значения, насколько она является широкой, симметричной т. п. , т. е. как элементы выборки рассеиваются, варьируются. Вариационных размах (интервал, амплитуда) – это разница между максимальным и минимальным значениями элементов выборки.

Показатели вариации Стандартное отклонение – это параметр, который характеризует степень разброса элементов выборки относительно среднего значения: п — объем выборки (количество вариантов в ней); х1 , х2, . . . , хп — все варианты выборки. х — среднее значение выборки. Величина 2 называется дисперсия

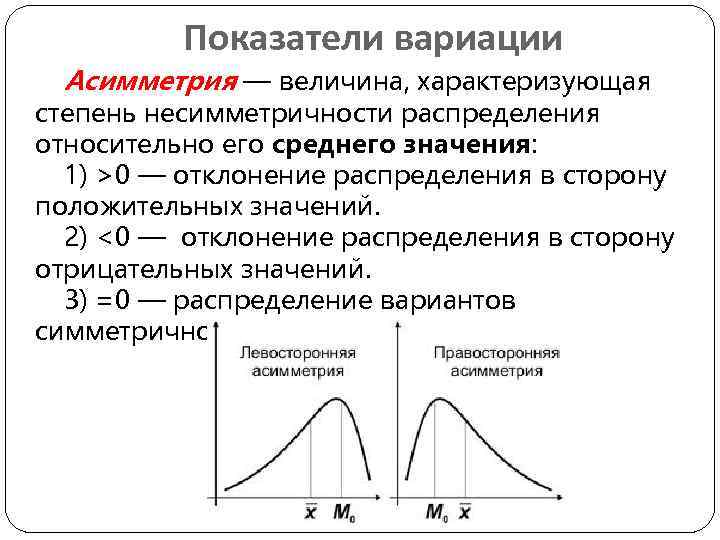
Показатели вариации Асимметрия — величина, характеризующая степень несимметричности распределения относительно его среднего значения: 1) >0 — отклонение распределения в сторону положительных значений. 2) <0 — отклонение распределения в сторону отрицательных значений. 3) =0 — распределение вариантов симметричное.

Связь обобщающих показателей с соответствующими показателями генеральной совокупности Предположение: генеральная совокупность имеет примерно те же значения этих показателей, что и выборка. Определить их – значит найти точечные оценки числовых характеристик генеральной совокупности.

Связь обобщающих показателей с соответствующими показателями генеральной совокупности Та или иная характеристика генеральной совокупности с определенной вероятностью принадлежит определенному интервалу вокруг значения, вычисленного по выборке. Определить такой интервал – значит найти интервальную оценку статистического показателя. Точечной оценкой стандартного отклонения генеральной совокупности является исправленное выборочное стандартное отклонение:

Статистические функции Excel 1) предназначены для вычисления обобщающих статистических характеристик выборки; 2) могут иметь до 30 аргументов, которые должны быть числами, массивами или ссылками на диапазоны ячеек, содержащих числа; 3) когда нужно вычислить определенную статистическую характеристику выборки, диапазон, содержащий элементы выборки, следует сделать аргументом функции.

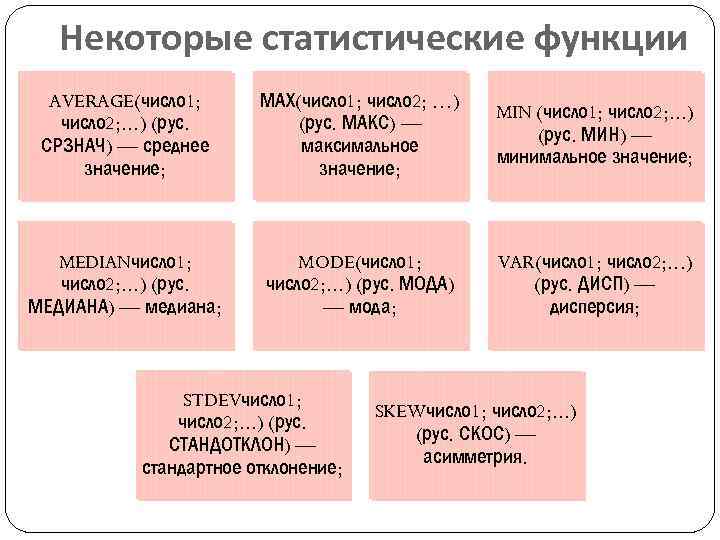
Некоторые статистические функции AVERAGE(число 1; число 2; . . . ) (рус. СРЗНАЧ) — среднее значение; МАХ(число 1; число 2; …) (рус. МАКС) — максимальное значение; MIN (число 1; число 2; . . . ) (рус. МИН) — минимальное значение; MEDIANчисло 1; число 2; . . . ) (рус. МЕДИАНА) — медиана; MODE(число 1; число 2; . . . ) (рус. МОДА) — мода; VAR(число 1; число 2; . . . ) (рус. ДИСП) — дисперсия; STDEVчисло 1; число 2; . . . ) (рус. СТАНДОТКЛОН) — стандартное отклонение; SKEWчисло 1; число 2; . . . ) (рус. СКОС) — асимметрия.

Вычисление статистических характеристик РАНГ(число; ссылка; порядок) – ранг числа в списке чисел, его номер в упорядоченной последовательности из указанного диапазона: q число — число, для которого определяется ранг; q ссылка — массив или ссылка на список чисел; q порядок — аргумент, определяющий способ упорядочения (если он отсутствует или равен 0, то наибольшее число имеет ранг 1, если не равен нулю, то ранг 1 имеет наименьшее число). РАНГ назначает повторяющимся числам одинаковый ранг. Если в списке целых чисел, отсортированных по возрастанию, дважды встречается 10 с рангом 5, число 11 имеет ранг 7, нет чисел ранга 6.