Спецкурс «Microsoft Excel в профильном обучении» Глава 7 "Решение задач на подбор параметра" 1 Excel у профільному навчанні
План понятие про численные методы решения задач; инструмент Подбор параметра; графически-численный метод решения уравнений. 2
Численные методы решения задач Численное решение уравнений и их систем состоит в приближённом определении корней уравнения или системы уравнений и применяется в случаях, когда точный метод решения неизвестен или трудоёмок. 3
Понятие задачи с параметром Во многих задачах определенный результат является известным, а значения параметров, при которых этот результат достигается, – нет. 4 Примеры: определить, через сколько часов скиснет молоко; при каком объеме выпуска продукции фирма получит прибыль в 1 000 грн; задачи на решение уравнений и неравенств; на поиск экстремумов.
Понятие целевой функции Во всех подобных задачах используется понятие целевой функции, которая должна: достичь определенного значения; Целе вая оптимизироваться (достичь минимума ячей ка или максимума). Зависит от параметров. Задача: подобрать такие значения параметров, при которых в целевой ячейке будет получен желаемый результат. 5
Использование средств подбора параметров Специальные средства табличного процессора Excel для автоматического подбора нужных значений в ячейках параметров: Подбор параметра: позволяет получить в целевой ячейке определенное значение. Поиск решения: позволяет оптимизировать значения целевой функции. 6
Применение средства Подбор параметра 1. В одну из ячеек (целевую) ввести формулу целевой функции. 2. Вкладка Данные, Работа с данными, «Анализ что-если» , Подбор параметра: Установить в ячейке – адрес целевой ячейки; Значение – значение, которое должна принять целевая функция; Изменяя значение ячейки – адрес клетки-параметра. 7
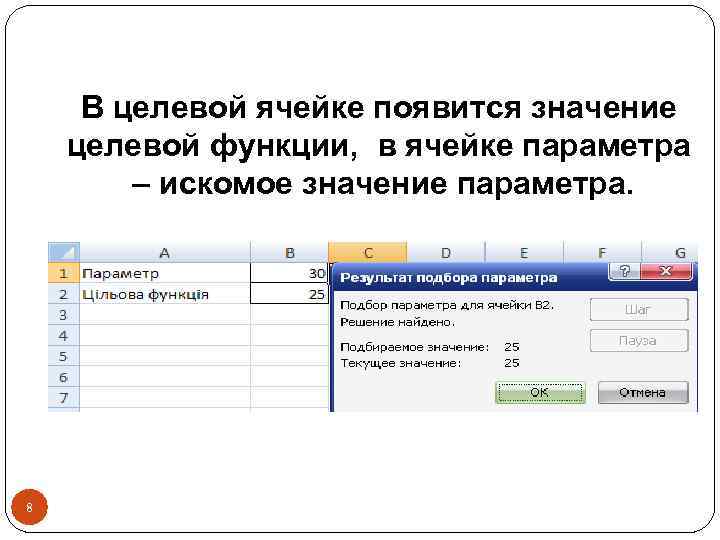
В целевой ячейке появится значение целевой функции, в ячейке параметра – искомое значение параметра. 8
Подбор параметра почти всегда дает приближенные значения результата. 5 4, 99999 1. Ячейку параметра можно оставить пустой. 2. Желательно предварительно определить некоторое начальное значение, от этого зависит скорость получения результата. 3. Если целевая функция сложная, несколько значений параметра могут соответствовать ее искомому значению определить начальное значение параметра построить график целевой функции. 9
Упражнение 7. 1. Решение уравнения 4 cos 2 x + 3 х = 15 1. Целевая функция: f (x) = 4 cos 2 x + 3 х, 15 – ее значение, т. е. f (x)=15. 2. Целевой считать ячейку В 2, пусть значение параметра хранится в ячейке В 1. 3. Ввести в В 2 формулу = 4 * cos (В 1) ^ 2 +3 * В 1 4. Выполнить команду Подбор параметра, заполнить поля в окне Подбор параметра, ОК. 10
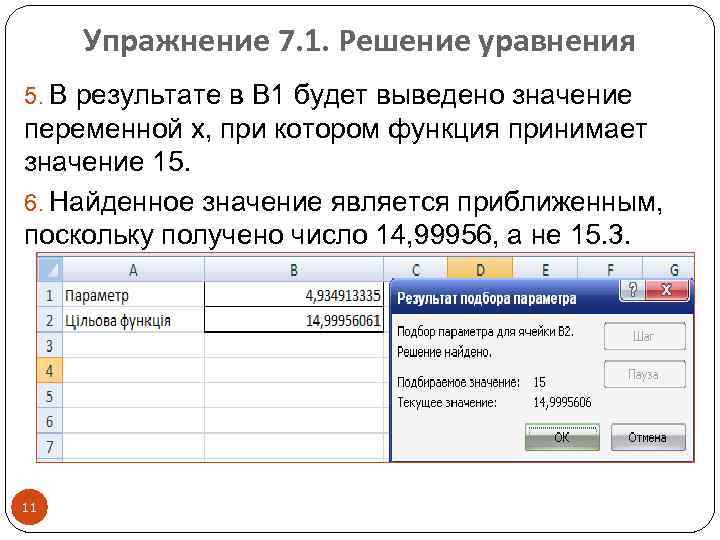
Упражнение 7. 1. Решение уравнения 5. В результате в В 1 будет выведено значение переменной х, при котором функция принимает значение 15. 6. Найденное значение является приближенным, поскольку получено число 14, 99956, а не 15. 3. 11
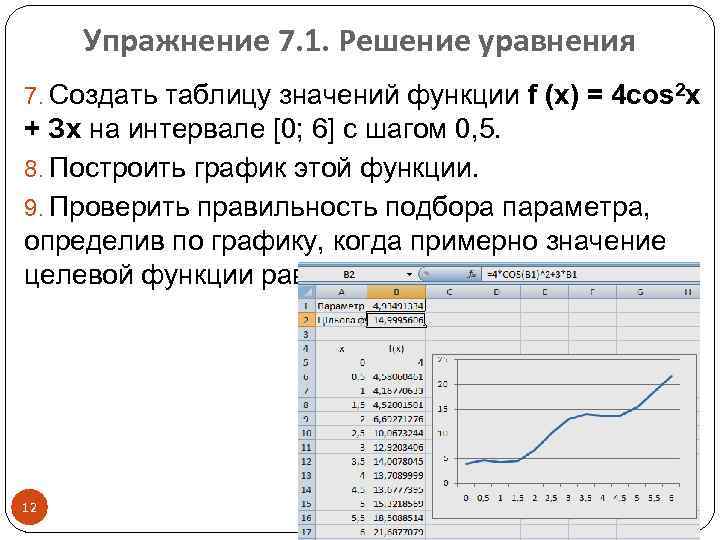
Упражнение 7. 1. Решение уравнения 7. Создать таблицу значений функции f (x) = 4 cos 2 x + Зх на интервале [0; 6] с шагом 0, 5. 8. Построить график этой функции. 9. Проверить правильность подбора параметра, определив по графику, когда примерно значение целевой функции равно 15. 12
Скачать презентацию Спецкурс Microsoft Excel в профильном обучении Глава 7
русspeckurs_et_rozdil_7.pptx