Устойчивость СЭ, лекции.ppt
- Количество слайдов: 76

Специальность 140211 - Электроснабжение Дисциплина: Устойчивость систем электроснабжения Шифр по учебному плану - ОПД. Р. 01

Предмет, цель и задача данной дисциплины Предметом курса являются методы анализа устойчивости динамических систем, в т. ч. технических средств автоматического управления и регулирования в системах электроснабжения. Цель - подготовка будущего специалиста в области применения методов и технических средств автоматического управления и регулирования в системах электроснабжения. Задачей изучения является приобретение знаний основ методов структурного моделирования динамических систем, методов анализа их устойчивости и качества регулирования в устройствах автоматики, применяемых в системах электроэнергетики и электроснабжения.

Раздел 1 Динамические системы и принципы автоматического управления и регулирования Понятие о динамических системах, их классификация Все технические устройства, включая электроэнергетические системы и системы электроснабжения, являются динамическими системами. Динамическими системами будем называть совокупность материальных объектов, текущее состояние которой определяется некоторым набором физических величин, изменяющихся во времени, причём эти физические величины связаны между собой. Связь может быть как статической, так и динамической. Будем различать системы с сосредоточенными и с распределенными параметрами. Система, состояние которой характеризуется физическими величинами, зависящими от времени и не зависящими от пространственных координат, определяющих её геометрические размеры, называется системой с сосредоточенными параметрами. Если физические величины, характеризующие состояние системы, зависят от пространственных координат, определяющих её геометрические размеры, то это – система с распределёнными параметрами.

Понятие о динамических системах, их классификация Наиболее важным классом динамических систем являются системы автоматического регулирования (САР) и системы автоматического управления (САУ). Они входят в состав всех электроэнергетических систем и систем электроснабжения. Задачей САУ является обеспечение некоторого наперёд заданного закона изменения физических величин. Примером САР может служить система стабилизации напряжения и частоты на выходе электрогенератора, работающего в составе централизованной или автономной электростанции. Примерами САУ могут служить системы управления электроприводами станков, транспортных средств, технологических установок и др. Важным классом САУ являются следящие системы, которые повторяют маломощные входные воздействия мощными выходными воздействиями. Например, система слежения за Солнцем концентратора светового потока в гелиотермической энергетической установке. Другой пример следящей системы – система слежения за целью для автоматического наведения оружия на цель. Динамические свойства САУ и САР могут быть описаны математической моделью, то есть оператором, характеризующим поведение реальной системы и отражающим все ее информационные свойства. В большинстве случаев математические модели могут базироваться на уравнениях и неравенствах различных типов: алгебраических, дифференциальных, интегральных, разностных. Часто этим уравнениям ставят в соответствие динамические характеристики: временные, частотные, операторные, в пространстве состояний.

Понятие о сигналах в динамических системах Любое управление тесно связано с таким понятием как информация. Информацией называют сообщение о том, что произошло некоторое событие. В частном случае это может быть сообщение о том, что некоторая физическая величина приняла определенное значение в определенный момент времени. Такую информацию называют измерительной. В связи с этим при анализе динамических систем приходится использовать понятие сигнала. Сигналом называется изменяющаяся во времени физическая величина, несущая на себе информацию. Нести информацию может не только мгновенное значение физической величины, но также и один или несколько параметров закона ее изменения во времени. Такие параметры называются информационными. Например, пусть напряжение изменяется по закону где могут изменяться во времени, следовательно, они могут быть информационными параметрами этого напряжения. Если информационным параметром синусоидального сигнала является амплитуда, то говорят, что это амплитудно-модулированный сигнал. Если информационным параметром синусоидального сигнала является частота, то говорят, что это частотно-модулированный сигнал. Если информационным параметром синусоидального сигнала является начальная фаза, то говорят, что это фазовая модуляция.

Типы сигналов Различают сигналы непрерывные и дискретные. Непрерывность и дискретность могут проявляться как по уровню, так и по времени. Сигнал называется непрерывным по уровню, если его информационные параметры могут принимать любые значения из заданного диапазона. Сигнал называется непрерывным по времени, если он существует и может изменяться в любой момент времени для заданного периода. Если сигнал является непрерывным по уровню и по времени, то он называется аналоговым сигналом. Сигнал называется дискретным по уровню, если его информационные параметры могут принимать конечное число дискретных значений в заданном диапазоне. Сигнал называется дискретным по времени, если он существует или может изменяться лишь в строго определенные моменты времени для заданного периода, причём в любом конечном временном интервале имеется конечное число таких моментов. Дискретный по уровню и по времени сигнал называется цифровым, если каждому возможному значению его информационного параметра поставлен во взаимнооднозначное соответствие цифровой код. Классы систем управления по типам сигналов Если процесс управления осуществляется только посредством аналоговых сигналов, то такая САР или САУ называется аналоговой. Если процесс управления осуществляется только посредством цифровых сигналов, то такая САР или САУ называется цифровой. В сложных системах автоматики могут комбинироваться аналоговый и цифровой принципы управления.

Понятие о функциональном элементе и функциональной схеме динамической системы Для анализа и синтеза динамические системы удобно представлять в виде функциональных схем, отражающих все информационные свойства системы. Такие схемы состоят из функциональных элементов, преобразующих некоторый набор входных сигналов в набор выходных сигналов. Схематичное изображение функционального элемента Функциональной схемой системы называется символическое изображение всех функциональных элементов технологического процесса управления и связей между ними.
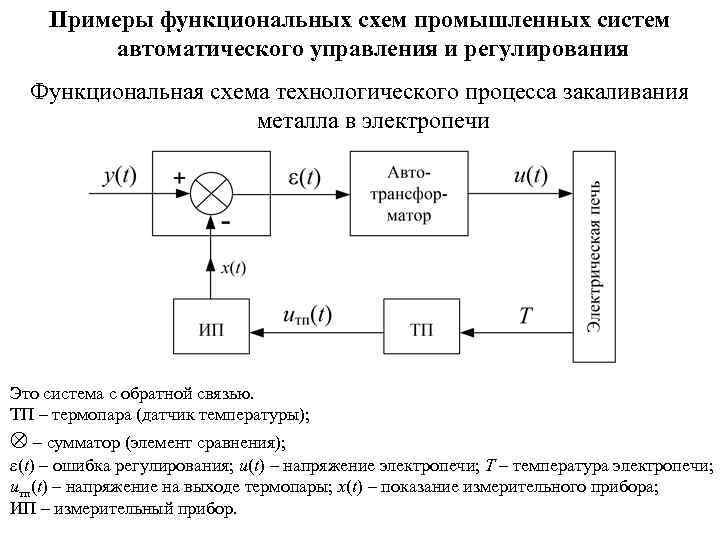
Примеры функциональных схем промышленных систем автоматического управления и регулирования Функциональная схема технологического процесса закаливания металла в электропечи Это система с обратной связью. ТП – термопара (датчик температуры); – сумматор (элемент сравнения); ε(t) – ошибка регулирования; u(t) – напряжение электропечи; T – температура электропечи; uтп(t) – напряжение на выходе термопары; x(t) – показание измерительного прибора; ИП – измерительный прибор.
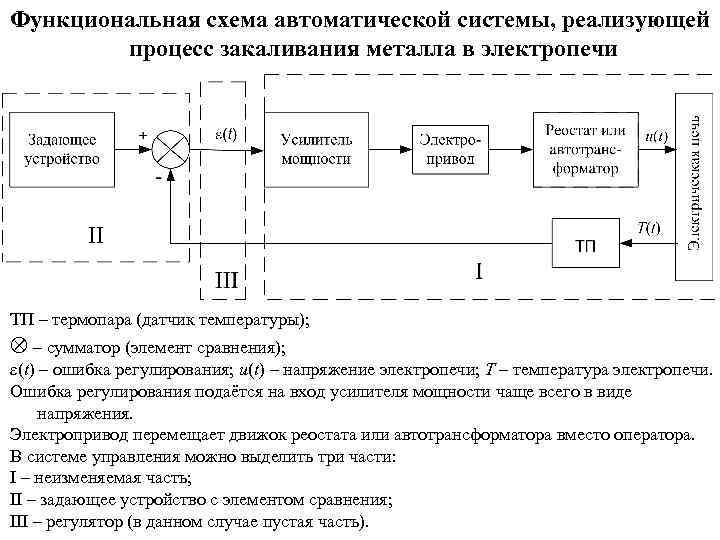
Функциональная схема автоматической системы, реализующей процесс закаливания металла в электропечи ТП – термопара (датчик температуры); – сумматор (элемент сравнения); ε(t) – ошибка регулирования; u(t) – напряжение электропечи; T – температура электропечи. Ошибка регулирования подаётся на вход усилителя мощности чаще всего в виде напряжения. Электропривод перемещает движок реостата или автотрансформатора вместо оператора. В системе управления можно выделить три части: I – неизменяемая часть; II – задающее устройство с элементом сравнения; III – регулятор (в данном случае пустая часть).

Три части системы управления с обратной связью I – неизменяемая часть: • объект управления (в данном случае – электропечь); • исполнительные устройства (в данном случае – реостат или автотрансформатор вместе с электроприводом); • устройства подготовки входных сигналов для исполнительных устройств (в данном случае – усилитель мощности); • измерительные устройства и измерительные преобразователи (в данном случае – термопара). II – задающее устройство с элементом сравнения. Эта часть может изменяться в зависимости от функционального назначения САУ и САР. III – регулятор (в данном случае – пустая часть). Сюда входят устройства, реализующие принцип управления и корректирующие устройства. Основные принципы управления в системах с обратной связью • • • пропорциональный принцип управления: П-регуляторы, интегральный принцип управления: И-регуляторы, пропорционально-интегральный принцип управления: ПИ-регуляторы, пропорционально-дифференциальный принцип управления: ПД-регуляторы, пропорционально-интегрально-дифференциальный принцип управления: ПИДрегуляторы. В представленной выше схеме реализован пропорциональный принцип управления.
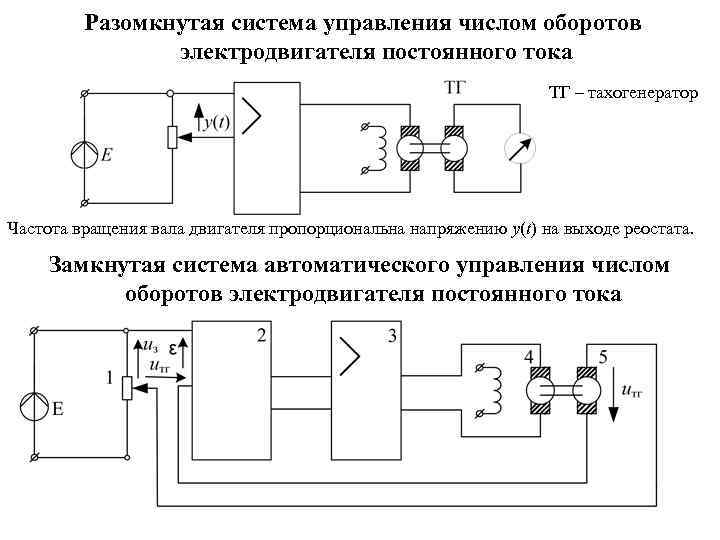
Разомкнутая система управления числом оборотов электродвигателя постоянного тока ТГ – тахогенератор Частота вращения вала двигателя пропорциональна напряжению y(t) на выходе реостата. Замкнутая система автоматического управления числом оборотов электродвигателя постоянного тока

Замкнутая система автоматического управления числом оборотов электродвигателя постоянного тока u. З – заданное напряжение, u. ТГ – напряжение якоря тахогенератора, 1 – задающее устройство (реостат), 2 – предварительный усилитель и регулятор, 3 – усилитель мощности, 4 – двигатель постоянного тока, являющийся объектом управления, 5 – тахогенератор, являющийся измерительной частью системы. Элементом сравнения в данной системе является контур электрической цепи, в котором действует второй закон Кирхгофа: В данной системе выходной физической величиной является частота вращения вала электродвигателя, которая поступает на вход измерительного преобразователя (тахогенератора), вал которого жёстко соединён с валом электродвигателя и механической нагрузки, которая на схеме не показана. В данной системе частота вращения регулируется напряжением якоря коллекторной машины постоянного тока. Возможно также регулирование током (магнитным потоком) возбуждения. В этом случае частота вращения будет нелинейно зависеть от тока возбуждения, значит, вся система будет нелинейной.

Цели и принципы управления Основной целью управления является обеспечение возможности изменять протекающие в объекте управления процессы путем воздействия на него соответствующими командами таким образом, чтобы была достигнута поставленная производственная или технологическая цель. Системой автоматического управления называется система, представляющая собой совокупность объекта управления и управляющего устройства, обеспечивающего процесс управления, то есть целенаправленное воздействие, приводящее к желаемому изменению управляемых переменных. фундаментальные принципы управления: 1) принцип разомкнутого управления, 2) принцип компенсации, 3) принцип обратной связи. Первый из этих принципов предполагает отсутствие в системе контуров управления элементов сравнения и регуляторов. Информация передаётся последовательно от задающего устройства к объекту управления. Других каналов и направлений передачи информации в системе не существует. Как правило, в системе отсутствует также измерительная часть или она служит только для визуального контроля. Второй принцип иначе называют принципом управления по возмущению. На объект управления объективно действуют не только управляющие сигналы, но и сигналы, нарушающие нормальный режим работы. Такие сигналы называются сигналами помехи или возмущающими воздействиями. Принцип компенсации возмущений основан на измерении возмущающих воздействий и соответствующей коррекции управляющих воздействий, чтобы минимизировать отклонения от нормальных и заданных режимов работы объектов.

В дальнейшем мы будем рассматривать только системы управления с обратными связями. Первые два типа систем управления характеризуются тем, что в них информация передаётся только в одном направлении, а в системах с обратной связью информация передаётся в двух направлениях. Принципиальные особенности САУ с обратной связью Для САУ этого класса характерно следующее: 1) Наличие обратной связи (информация передаётся в двух направлениях). 2) Слабые управляющие сигналы на входе (по мощности), идущие от измерительного устройства (или задающего устройства), преобразуются в достаточно мощное воздействие на объект. Пример. Солнечная энергетическая установка (гелиотермического типа) с концентратором светового потока. В этой системе есть следящая система за солнцем – механический усилитель мощности. Она (система) преобразует слабый сигнал в мощное воздействие на привод. 3) Ошибка управления ε(t) является движущим фактором для системы, работающей на уменьшение этой ошибки. 4) САУ является замкнутой системой. Замыкание здесь осуществляется через обратную связь, которая реализуется с помощью измерительного устройства. Измерительный (чувствительный) элемент служит не просто для регистрации управляемой величины, но и для формирования сигнала рассогласования, то есть ошибки, являющегося входом усилителя и таким образом реализующего процесс управления.
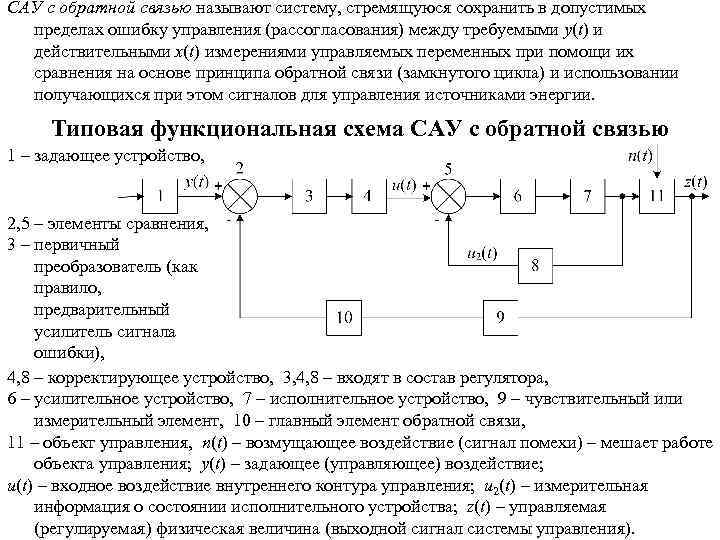
САУ с обратной связью называют систему, стремящуюся сохранить в допустимых пределах ошибку управления (рассогласования) между требуемыми y(t) и действительными x(t) измерениями управляемых переменных при помощи их сравнения на основе принципа обратной связи (замкнутого цикла) и использовании получающихся при этом сигналов для управления источниками энергии. Типовая функциональная схема САУ с обратной связью 1 – задающее устройство, 2, 5 – элементы сравнения, 3 – первичный преобразователь (как правило, предварительный усилитель сигнала ошибки), 4, 8 – корректирующее устройство, 3, 4, 8 – входят в состав регулятора, 6 – усилительное устройство, 7 – исполнительное устройство, 9 – чувствительный или измерительный элемент, 10 – главный элемент обратной связи, 11 – объект управления, n(t) – возмущающее воздействие (сигнал помехи) – мешает работе объекта управления; y(t) – задающее (управляющее) воздействие; u(t) – входное воздействие внутреннего контура управления; u 2(t) – измерительная информация о состоянии исполнительного устройства; z(t) – управляемая (регулируемая) физическая величина (выходной сигнал системы управления).

Раздел 2 Методы анализа и моделирования свойств функциональных элементов и динамических систем Динамические свойства функциональных элементов могут быть описаны: • системами дифференциальных и алгебраических уравнений; • переходными и импульсными характеристиками элемента; • передаточными функциями линейных стационарных элементов; • комплексными частотными характеристиками; • в пространстве состояния. Это означает, что динамические свойства можно представить во временной области и в частотной области. Динамическое звено Динамическим звеном будем называть обобщённый функциональный элемент, имеющий один скалярный вход и один скалярный выход. Представление функциональной схемы САУ в виде схемы, содержащей такие динамические звенья, называется структурным моделированием динамической системы. Если динамическое звено описано линейным дифференциальным или алгебраическим уравнением, то такое звено называют линейным, и динамические свойства этого звена могут быть описаны передаточными функциями, а также временными и частотными характеристиками.

Связь между дифференциальным уравнением линейного динамического звена и его передаточной функцией, а также комплексной частотной характеристикой Пусть линейное стационарное динамическое звено описывается дифференциальным уравнением вида Тогда передаточная функция этого звена может быть представлена следующей дробью: Передаточная функция, соответствующая линейному дифференциальному уравнению с постоянными коэффициентами является дробно-рациональной функцией комплексной частоты. У реальных стационарных динамических звеньев всегда n>=m, а чаще всего n>m. Если в передаточной функции комплексную частоту s заменить на jω, где ω – циклическая частота синусоидального колебания, то получим выражение для комплексной частотной характеристики звена H(jω).

Комплексная частотная характеристика динамического звена Комплексной частотной характеристикой (КЧХ) называется частотная зависимость комплексного коэффициента передачи сигнала со входа на выход. Иначе КЧХ называется амплитудно-фазочастотной характеристикой (АФЧХ). Модуль комплексной частотной характеристики H(ω) = |H(jω)| называется амплитудно-частотной характеристикой (АЧХ). Аргумент КЧХ называется фазочастотной характеристикой (ФЧХ). Это частотная зависимость разности фаз выходного и входного сигнала звена. Если частоты, а также модули коэффициентов передачи сигналов отобразить в логарифмическом масштабе, то АЧХ будет называться логарифмической амплитудно-частотной характеристикой (ЛАЧХ). Если частоты отобразить в логарифмическом масштабе, а разности фаз выходного и входного сигнала отобразить в линейном масштабе, то получится логарифмическая фазочастотная характеристика (ЛФЧХ). При графическом построении логарифмических частотных характеристик отношения частот и отношения коэффициентов передачи могут выражаться в специальных логарифмических единицах: для частот – декады, октавы; для коэффициентов передачи – децибелы, неперы. Декадой называется непрерывный частотный диапазон, верхняя граничная частота которого больше нижней в 10 раз. Октавой называется непрерывный частотный диапазон, верхняя граничная частота которого в 2 раза больше нижней.

Представление частотных диапазонов в логарифмическом масштабе На графике ось частоты (горизонтальная ось) может размечаться в логарифмическом масштабе, например: Представление коэффициентов передачи в логарифмическом масштабе Коэффициенты передачи и их отношения могут измеряться в логарифмических единицах: децибелах и неперах: Говорят, что коэффициент передачи Н 2 на частоте 2 на 20 д. Б больше, чем коэффициент передачи Н 1 на частоте 1, если Н 2/Н 1 = 10. Говорят, что коэффициент передачи сигнала Н 2 на частоте 2 на 1 Нп больше, чем коэффициент передачи Н 1 на частоте 1, если Н 2/Н 1 = е (основание натурального логарифма). Единичная функция Единичной функцией называется функция вида иначе её называют функцией единичного скачка. Другое название – функция Хевисайда (Heaviside). Эту функцию удобно использовать для математического представления сигналов с разрывами первого рода.

Дельта-функция Дирака (Dirac) Дельта-функцией называется функция вида Иначе эту функцию называют единичным импульсом. Дельта функция Дирака представляет собой бесконечно короткий импульс с бесконечно большой амплитудой. Для него выполняется следующее соотношение: -функция Дирака – предельный случай прямоугольного импульса, амплитуда которого является величиной, обратной длительности, причем длительность стремится к нулю. -функция является производной по времени от единичной функции. Переходная и импульсная характеристики линейного динамического звена Реакция динамического звена на входное воздействие, представляющее собой единичную функцию, называется переходной характеристикой динамического звена. Реакция динамического звена на входное воздействие, представляющее собой -функцию, называется импульсной характеристикой звена. Импульсная характеристика звена является производной по времени от переходной характеристики.

Переходная и импульсная характеристики линейного динамического звена где h(t) - импульсная характеристика, g(t) - переходная характеристика. Импульсная характеристика звена равна обратному преобразованию Лапласа от передаточной функции: Сигнальные графы и структурные схемы динамических систем Система линейных уравнений (алгебраических или дифференциальных), описывающая процессы в динамической системе может быть наглядно представлена в виде сигнального графа. Сигнальным графом называется направленный граф, находящийся в однозначном соответствии с системой линейных уравнений (в некоторых случаях – нелинейных уравнений). Пусть дана система n-линейных уравнений: Введём обозначения: С учетом введённых обозначений систему линейных уравнений можно представить в виде
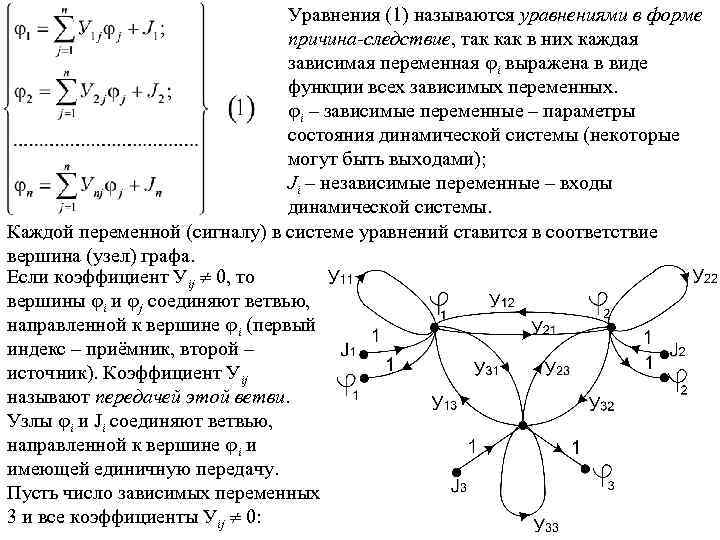
Уравнения (1) называются уравнениями в форме причина-следствие, так как в них каждая зависимая переменная i выражена в виде функции всех зависимых переменных. i – зависимые переменные – параметры состояния динамической системы (некоторые могут быть выходами); Ji – независимые переменные – входы динамической системы. Каждой переменной (сигналу) в системе уравнений ставится в соответствие вершина (узел) графа. Если коэффициент Уij 0, то вершины i и j соединяют ветвью, направленной к вершине i (первый индекс – приёмник, второй – источник). Коэффициент Уij называют передачей этой ветви. Узлы i и Ji соединяют ветвью, направленной к вершине i и имеющей единичную передачу. Пусть число зависимых переменных 3 и все коэффициенты Уij 0:

Основные понятия теории сигнальных графов Ветви, которые начинаются и заканчиваются в одном и том же узле, называются петлями. Узел сигнального графа, к которому присоединены только исходящие ветви, называется истоком. Узел сигнального графа, к которому присоединены только входящие ветви, называется стоком. Узлы, к которым присоединены входящие и выходящие ветви, называются промежуточными. Любой промежуточный узел можно преобразовать в сток путем добавления ветви с единичной передачей. Истокам сигнального графа соответствуют входы динамической системы. Стокам сигнального графа соответствуют выходы динамической системы. Промежуточным узлам соответствуют параметры состояния системы. Анализ системы с помощью сигнального графа сводится к вычислению передач от истоков к стокам. Передачей сигнального графа от истока к стоку называется отношение сигнала в стоке к сигналу в истоке при условии, что во всех остальных истоках сигналы равны нулю. Передачи от истоков к стокам могут быть рассчитаны путем исключения промежуточных узлов. Исключение узла соответствует исключению зависимой переменной в системе уравнений.

Переход от сигнального графа к структурной схеме Сигнальному графу можно поставить в однозначное соответствие структурную схему динамической системы. Пусть имеется два узла, соединённых ветвью: На структурной схеме данному фрагменту графа соответствует следующее: Узлу сигнального графа (сигналу) соответствует стрелка на структурной схеме. Ветви сигнального графа (передаче) соответствует блок структурной схемы. Каждую характеристику передачи записывают внутри прямоугольника. В данном случае это передаточная функция H(s). В более общем случае это может быть любой из возможных способов описания динамических свойств блока. Тогда внутри прямоугольника записывают уравнение преобразования сигнала u в сигнал x либо делают ссылку на это уравнение или соответствующую математическую модель. Если в один узел сигнального графа входит более одной ветви, то такой узел на структурной схеме представляется сумматором, выходным сигналом которого является сигнал данного узла. Входными сигналами сумматора являются выходные сигналы ветвей, входящих в узел. На сигнальном графе эти сигналы не показываются.
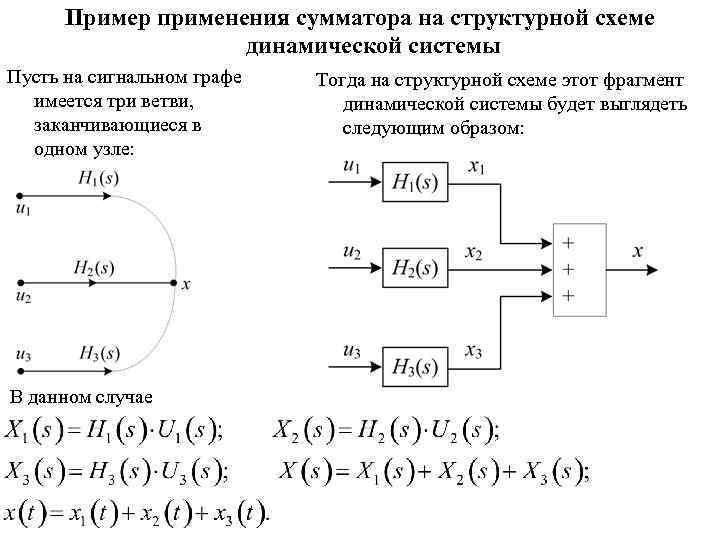
Пример применения сумматора на структурной схеме динамической системы Пусть на сигнальном графе имеется три ветви, заканчивающиеся в одном узле: В данном случае Тогда на структурной схеме этот фрагмент динамической системы будет выглядеть следующим образом:

Формула Мэзона Передача сигнального графа может быть непосредственно определена с помощью топологической формулы, которую называют формулой Мэзона. Для этого вводятся следующие понятия. Путь сигнального графа (направленный путь) – непрерывная последовательность ветвей графа между двумя различными узлами при условии, что начальный узел каждой ветви, кроме первой, совпадает с конечным узлом предыдущей. Каждый узел и ветвь в этой последовательности встречаются только один раз. Начало первой ветви считают начальным узлом пути, а конец последней ветви – конечным узлом пути. Прямой путь (путь передачи) – путь сигнального графа, начинающийся в истоке и заканчивающийся в стоке. Передача прямого пути П’k – это произведения передач этого пути. Контур – замкнутый путь сигнального графа, у которого начальный и конечный узлы совпадают. Передача контура Lk – произведение передач ветвей этого контура. Определитель сигнального графа ( ) – определитель системы уравнений, отображаемых графом. Минор прямого пути ( ’k) – определитель графа, получаемого из исходного графа, при исключении ветвей прямого пути и ветвей, имеющих с ним общие узлы. Иначе говоря, минор прямого пути – это определитель той части графа, которая не соприкасается с прямым путём.

Формула Мэзона В связи с введенными понятиями топологическая формула для передачи сигнального графа имеет вид: Здесь суммирование проводят по всем прямым путям. Определитель сигнального графа можно вычислить по формуле: – сумма передач всех контуров сигнального графа. сумма произведений передач всех возможных комбинаций из r некасающихся контуров. Миноры ’k вычисляются по формуле (3). Методы построения сигнальных графов электрических цепей Наиболее подробно мы рассмотрим построение графа уравнений Кирхгофа электрической цепи. Сигнальный граф, соответствующий уравнениям Кирхгофа, строится следующим образом:

• • выбирается дерево схемы; после этого напряжения ветвей связи выражают через напряжения ветвей дерева по второму закону Кирхгофа; • токи ветвей дерева выражают через токи ветвей связи по первому закону Кирхгофа; • напряжения ветвей дерева выражают через соответствующие токи по закону Ома; • токи ветвей связи выражают через соответствующие напряжения по закону Ома. В результате получится 2 в уравнений, содержащих 2 в неизвестных переменных. Записаны эти уравнения в форме причина-следствие. Полученной системе уравнений соответствует сигнальный граф, содержащий 2 в промежуточных узлов. Число истоков в графе равно числу источников в анализируемой цепи. Пусть имеется схема электрической цепи. В соответствии с записанными уравнениями сигнальный граф уравнений Кирхгофа для данной электрической цепи имеет следующий вид:
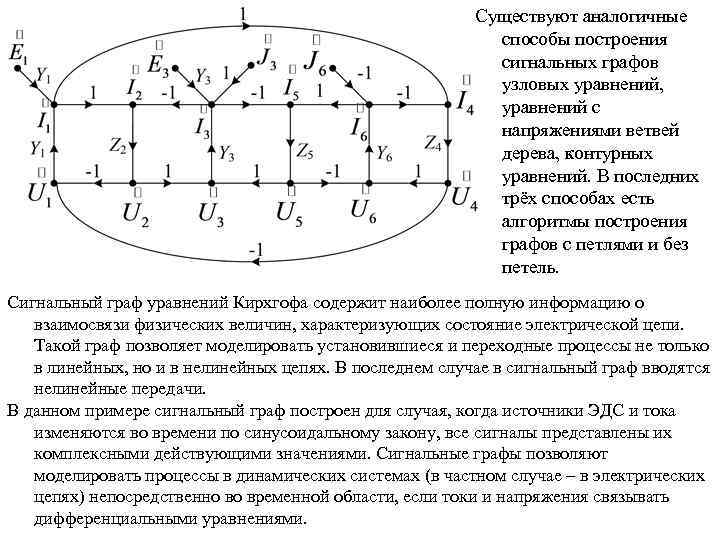
Существуют аналогичные способы построения сигнальных графов узловых уравнений, уравнений с напряжениями ветвей дерева, контурных уравнений. В последних трёх способах есть алгоритмы построения графов с петлями и без петель. Сигнальный граф уравнений Кирхгофа содержит наиболее полную информацию о взаимосвязи физических величин, характеризующих состояние электрической цепи. Такой граф позволяет моделировать установившиеся и переходные процессы не только в линейных, но и в нелинейных цепях. В последнем случае в сигнальный граф вводятся нелинейные передачи. В данном примере сигнальный граф построен для случая, когда источники ЭДС и тока изменяются во времени по синусоидальному закону, все сигналы представлены их комплексными действующими значениями. Сигнальные графы позволяют моделировать процессы в динамических системах (в частном случае – в электрических цепях) непосредственно во временной области, если токи и напряжения связывать дифференциальными уравнениями.

Описание динамической системы в пространстве состояний Одним из способов описания динамических свойств системы является описание в пространстве состояний. Полная система дифференциальных и алгебраических уравнений динамической системы преобразуется к системе уравнений первого порядка. Если динамическая система линейная стационарная с сосредоточенными параметрами, то уравнения в пространстве состояний имеют вид: [x(t)] – матрица-столбец переменных состояния, размерность - (n х 1), где n – количество переменных состояния; [y(t)] – матрица-столбец выходных переменных динамической системы, размерность (р х 1), где p – количество выходов; [u(t)] – матрица-столбец входных переменных динамической системы, размерность (r х 1), где r – количество входов; [A] – матрица коэффициентов динамической системы, [n x n]; [B] – матрица входов, [n x r]; [С] – матрица выходов, [p x n]; [D] – матрица обходов, [p x r].

Управляемость и наблюдаемость динамической системы Моделирование динамических систем позволяет анализировать управляемость и наблюдаемость динамической системы. Система называется вполне управляемой, если выбором управляющих воздействий [u(t)] на интервале времени [t 0, t 1] можно перевести систему из любого начального состояния [x(t 0)] в произвольное заранее заданное конечное состояние [x(t 1)]. Система называется вполне наблюдаемой, если по реакции [y(t 1)] на выходе системы на интервале времени [t 0, t 1] при заданном управляющем воздействии [u(t)] можно определить начальное состояние [x(t 0)]. Критерий управляемости линейных систем Для того чтобы система была вполне управляемой, необходимо и достаточно, чтобы ранг матрицы управляемости равнялся размерности матрицы состояния: rank ([MU]) = n Критерий наблюдаемости линейных систем Для того чтобы система была вполне наблюдаемой, необходимо и достаточно, чтобы ранг матрицы наблюдаемости равнялся размерности матрицы состояния: rank ([MY]) = n

Нелинейное обобщение описания динамической системы в пространстве состояний Уравнения динамических систем в пространстве состояний могут обобщаться на нелинейный случай. Возможны разные варианты такого обобщения: где f – скалярная нелинейная функция. Возможен более простой вариант: где f – нелинейная функция, возвращающая матрицу-столбец. Возможны более простые варианты: где f 1, f 2, g 1, g 2, g 3, g 4 – нелинейные функции, возвращающие матрицы-столбцы.
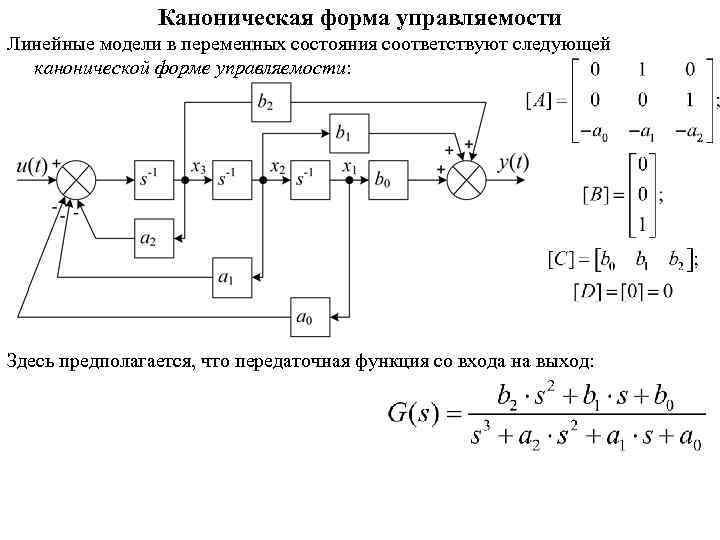
Каноническая форма управляемости Линейные модели в переменных состояния соответствуют следующей канонической форме управляемости: Здесь предполагается, что передаточная функция со входа на выход:
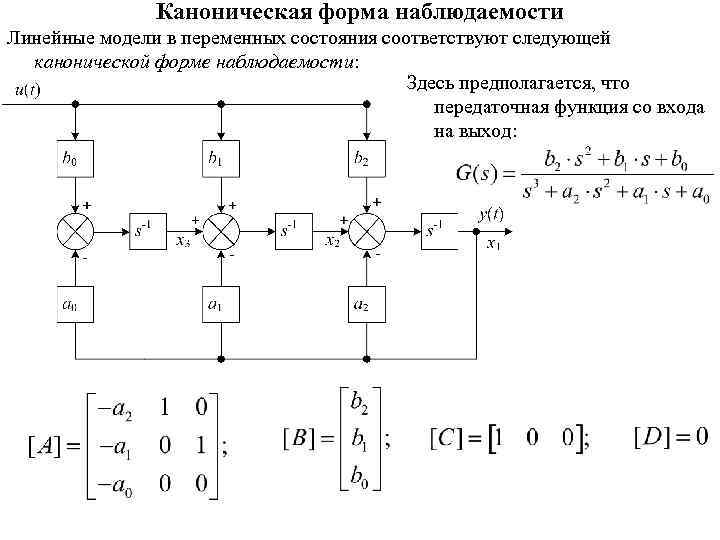
Каноническая форма наблюдаемости Линейные модели в переменных состояния соответствуют следующей канонической форме наблюдаемости: Здесь предполагается, что передаточная функция со входа на выход:

Раздел 4 Критерии устойчивости динамических систем. Качество регулирования Необходимое и достаточное условие устойчивости линейной стационарной динамической системы Любая динамическая система технически работоспособна только в том случае, если она устойчива. Система является устойчивой, если при любом ограниченном входном сигнале выходной сигнал также является ограниченным во все моменты времени (все параметры состояния системы ограничены во все моменты времени). Система управления называется устойчивой по Ляпунову, если при любых ненулевых ограниченных начальных условиях свободная составляющая переходного процесса в системе ограничена. Если динамическая система является линейной стационарной и если она устойчива по Ляпунову, то она устойчива в общем случае. Линейная стационарная динамическая система описывается линейными дифференциальными уравнениями с постоянными коэффициентами. Система является устойчивой тогда и только тогда, когда действительные части корней характеристического уравнения, соответствующего системе дифференциальных уравнений, отрицательны. В этом случае все слагаемые общего решения для свободной составляющей переходного процесса стремятся к нулю при времени, стремящемся к бесконечности.

Необходимое и достаточное условие устойчивости … Как известно, линейному дифференциальному уравнению n-го порядка с постоянными коэффициентами можно поставить в однозначное соответствие передаточную функцию, полюса которой равны корням характеристического уравнения. В связи с этим необходимое и достаточное условие устойчивости линейных стационарных динамических систем можно сформулировать так: система является устойчивой тогда и только тогда, когда действительные части всех полюсов передаточной функции отрицательны. В этом случае все слагаемые импульсной характеристики системы стремятся к нулю при времени, стремящемся к бесконечности. Полюса передаточной функции устойчивой линейной стационарной системы называются левыми полюсами, так как они на комплексной плоскости находятся слева от мнимой оси. Если действительная часть полюса положительна, то такой полюс называется правым. Если передаточная функция имеет хотя бы один правый полюс, то система неустойчива, так как в этом случае, по крайней мере, одно из слагаемых импульсной характеристики стремится к бесконечности при времени, стремящемся к бесконечности. Если некоторые полюса передаточной функции имеют нулевую действительную часть, то система находится на границе устойчивости. В этом случае импульсная характеристика в установившемся режиме представляет собой либо постоянную функцию времени, либо незатухающие периодические колебания. Если все полюса передаточной функции действительны, то переходные процессы в системе происходят без свободных колебаний. Если хотя бы два полюса передаточной функции комплексные, то свободная составляющая переходных процессов имеет колебательные составляющие.

Алгебраические критерии устойчивости Критерий Рауса Непосредственное применение необходимого и достаточного условия устойчивости может сопровождаться некоторыми трудностями, связанными с необходимостью вычисления корней полиномов высокого порядка. Данная процедура во многих случаях является численно неустойчивой. Алгебраические критерии устойчивости позволяют выявить наличие правых или мнимых (центральных) полюсов по коэффициентам знаменателя передаточной функции замкнутой системы без вычисления этих полюсов. Критерий Рауса позволяет аналитически определить, все ли корни полинома знаменателя имеют отрицательные действительные части, а если нет, то сколько корней имеют положительную действительную часть. Этот критерий не может применяться, когда система имеет в своем составе идеальные запаздывающие динамические звенья. Критерий Рауса применяется к полиному вида: Q(s) = an sn + an-1 sn-1 + … + a 1 s + a 0. Здесь мы предполагаем, что a 0 0, так как в противном случае полином имеет хотя бы один нулевой корень, а значит, система находится на границе устойчивости. В начале составляется таблица (матрица) Рауса

Вычисления продолжаются до тех пор, пока число строк в матрице Рауса не достигнет n+1. Вывод о количестве правых полюсов передаточной функции можно сделать из анализа первого столбца матрицы Рауса. Критерий Рауса формулируется следующим образом: число правых корней полинома равно числу перемен знака в первом столбце матрицы Рауса. Частные случаи применения критерия Рауса Из выражений для определения элемента матрицы Рауса видно, что таблица не может быть заполнена, если первый элемент в строке равен нулю. В этом случае вычисление элементов следующей строки связано с делением на нуль. Учитывая возможность данной ситуации в практическом применении критерия, следует выделить три случая.

Частные случаи применения критерия Рауса Случай первый. Ни один из элементов первого столбца матрицы Рауса не равен нулю. Это нормальный случай вычисления. Здесь возможно прямое применение формул для вычисления элементов матрицы Рауса. Случай второй. Первый элемент строки матрицы Рауса равен нулю, и хотя бы один другой элемент этой строки не равен нулю. В этом случае первый элемент строки заменяется на ненулевую бесконечно малую величину, знак которой берётся совпадающим со знаком предыдущего элемента первого столбца. Вычисления продолжаются, но некоторые элементы матрицы Рауса теперь будут зависеть от этой бесконечно малой величины . После окончания вычислений определим пределы выражений, зависящих от при 0. После этого можно определять число перемен знака в первом столбце матрицы и делать вывод об устойчивости. Пример: пусть в знаменателе передаточной функции замкнутой системы стоит полином Q(s) = s 5 + 2 s 4 + 2 s 3 + 4 s 2 + 11 s + 10. Матрица Рауса 1 2 11 2 4 10 6 0 - 10 0 6 0 10 0 Две перемены знака, следовательно, система неустойчивая.

Частные случаи применения критерия Рауса Случай третий. Все элементы строки матрицы Рауса равны нулю. В этом случае замена нуля бесконечно малой величиной не позволяет проводить дальнейшие вычисления. При вычислении матрицы Рауса нули заменяются коэффициентами, которые получаются в результате дифференцирования по s дополнительного полинома, относящегося к предыдущей строке. Пример № 1. Q(s) = s 2 + 1. Данный полином имеет два мнимых корня: -j и j, а правых корней нет, значит, соответствующая система находится на границе устойчивости. Матрица Рауса имеет вид: Дополнительный полином, соответствующий первой строке, равен Q(s), его производная равна 2 s. С учётом этого матрица Рауса приобретает вид Пример № 2. Q(s) = s 3 + s 2 + 2 s + 2. Первые две строки матрицы Рауса имеют вид Если дальше вычислять по обычной формуле заполнения, то следующая строка станет равной нулю. Поэтому следующую строку будем вычислять путём дифференцирования дополнительного полинома, соответствующего строке 2. Вся матрица имеет вид В первом столбце матрицы Рауса перемен знака нет, значит, полином Q(s) не имеет правых полюсов.

Критерий Гурвица Этот критерий основан на составлении матрицы Гурвица. Пусть передаточная функция замкнутой системы имеет вид: Тогда матрица Гурвица имеет вид Определитель матрицы Гурвица называется главным определителем Гурвица. Его миноры называются определителями Гурвица низшего порядка. Размер матрицы Гурвица – (n n).

Формулировка критерия Гурвица Для того, чтобы замкнутая система была устойчивой, необходимо и достаточно, чтобы при а 0>0 все определители Гурвица были положительными. Система находится на границе устойчивости, если все определители Гурвица низшего порядка положительны, а главный определитель Гурвица равен нулю (при а 0>0). Если a 0>0, an=0, n-1>0, то один из корней характеристического уравнения равен нулю. В этом случае говорят, что система находится на границе апериодической устойчивости. Если же an 0, а n-1>0, то у характеристического уравнения есть хотя бы одна пара мнимых комплексно-сопряжённых корней. В этом случае говорят, что система находится на границе колебательной устойчивости. Необходимым и достаточным условием устойчивости системы, характеристическое уравнение которой, а значит, и знаменатель передаточной функции замкнутой системы, имеет первую и вторую степень, является положительность всех коэффициентов характеристического уравнения. Критерий Льенара-Шипара Пусть передаточная функция замкнутой системы имеет вид (1). Здесь опять составляется матрица Гурвица. При положительных коэффициентах знаменателя передаточной функции (1) необходимое и достаточное условие устойчивости сводится к тому, чтобы среди определителей Гурвица ∆k, где k=1. . n, были положительными все определители с чётными индексами либо все определители Гурвица с нечётными индексами.

Анализ устойчивости в частотной области Критерий устойчивости в частотной области применяется к КЧХ разомкнутой системы. Структурная схема динамической системы путём эквивалентных преобразований приводится к одноконтурному виду: G(s) – передаточная функция прямого тракта системы; H(s) – передаточная функция отрицательной обратной связи. Передаточная функция разомкнутой системы равна произведению этих функций: В соответствии с формулой Мэзона передаточная функция замкнутой системы равна Из этого следует, что полюса передаточной функции замкнутой системы являются нулями функции 1+Hp(s). Значит, характеристическое уравнение замкнутой системы имеет вид Hp(s) = -1. КЧХ получается из передаточной функции путём замены s на j , где - циклическая частота синусоидального сигнала, подаваемого на вход системы. Геометрическое место точек на комплексной плоскости, соответствующее значениям комплексного коэффициента передачи сигнала при изменении частоты от 0 до , называется годографом КЧХ.

Годограф КЧХ, построенный при изменении частоты от 0 до , а затем от - до нуля, называется диаграммой Найквиста. По виду диаграммы Найквиста разомкнутой системы можно определить устойчивость замкнутой системы. Критерий устойчивости Найквиста Число правых полюсов передаточной функции замкнутой системы определяется по формуле Z = N 1–N 2+P, где N 1 – число охватов по часовой стрелке диаграммой Найквиста разомкнутой системы точки -1; N 2 – число охватов против часовой стрелки диаграммой Найквиста разомкнутой системы точки -1; P – число правых полюсов передаточной функции разомкнутой системы. В любом случае Z 0. Система устойчива, если Z = 0. Если при Z = 0 диаграмма Найквиста разомкнутой системы при увеличении частоты и при движении по часовой стрелке проходит через точку -1, то замкнутая система находится на границе устойчивости. Если разомкнутая система неустойчивая (P>0), то замкнутая система может быть устойчивой только в том случае, когда N 1–N 2 = –P. Данный случай часто имеет место в системах управления движением ракет. Пусть разомкнутая система имеет передаточную функцию третьего порядка: k = b 0/a 0 – статический коэффициент передачи разомкнутой системы.
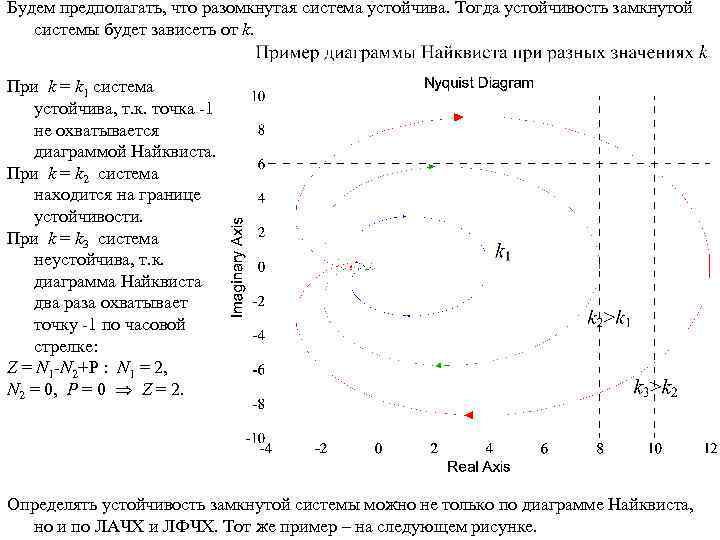
Будем предполагать, что разомкнутая система устойчива. Тогда устойчивость замкнутой системы будет зависеть от k. При k = k 1 система устойчива, т. к. точка -1 не охватывается диаграммой Найквиста. При k = k 2 система находится на границе устойчивости. При k = k 3 система неустойчива, т. к. диаграмма Найквиста два раза охватывает точку -1 по часовой стрелке: Z = N 1 -N 2+P : N 1 = 2, N 2 = 0, P = 0 Z = 2. Определять устойчивость замкнутой системы можно не только по диаграмме Найквиста, но и по ЛАЧХ и ЛФЧХ. Тот же пример – на следующем рисунке.
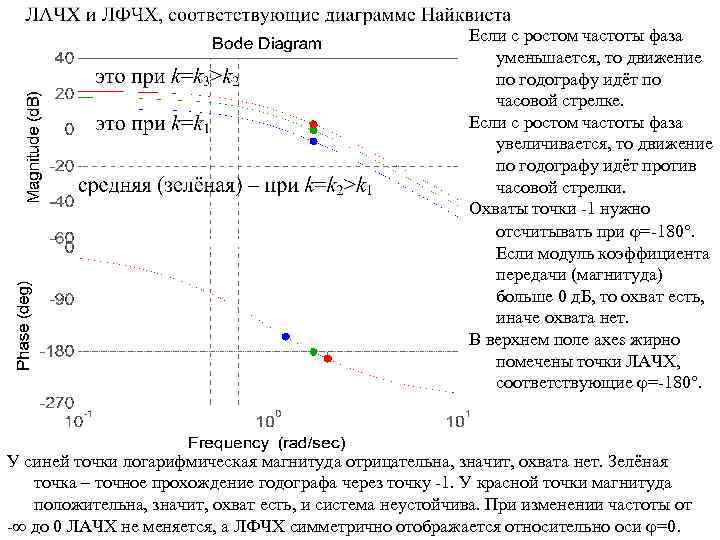
Если с ростом частоты фаза уменьшается, то движение по годографу идёт по часовой стрелке. Если с ростом частоты фаза увеличивается, то движение по годографу идёт против часовой стрелки. Охваты точки -1 нужно отсчитывать при =-180. Если модуль коэффициента передачи (магнитуда) больше 0 д. Б, то охват есть, иначе охвата нет. В верхнем поле axes жирно помечены точки ЛАЧХ, соответствующие =-180. У синей точки логарифмическая магнитуда отрицательна, значит, охвата нет. Зелёная точка – точное прохождение годографа через точку -1. У красной точки магнитуда положительна, значит, охват есть, и система неустойчива. При изменении частоты от - до 0 ЛАЧХ не меняется, а ЛФЧХ симметрично отображается относительно оси =0.

Движение по кривым ЛАЧХ и ЛФЧХ теперь должно идти справа налево. Синяя кривая – опять нет охвата. Зелёная кривая – опять точное прохождение через точку -1. Красная кривая – опять охват по часовой стрелке. Итог: синяя кривая соответствует устойчивой системе, зелёная – границе устойчивости (два центральных полюса передаточной функции замкнутой системы), красная соответствует неустойчивой системе (Z=2). Диаграмма Боде для разомкнутой системы позволяет оценивать запасы и дефициты устойчивости замкнутой системы. Для устойчивой системы запас устойчивости по модулю показывает, на сколько в логарифмическом масштабе можно увеличить статический коэффициент передачи разомкнутой системы, чтобы замкнутая система дошла до границы устойчивости, и дальнейшее увеличение этого коэффициента привело бы к потере устойчивости. Для неустойчивой системы дефицит устойчивости по модулю показывает, на сколько в логарифмическом масштабе можно уменьшить статический коэффициент передачи разомкнутой системы, чтобы замкнутая система дошла до границы устойчивости, и дальнейшее уменьшение этого коэффициента привело бы к тому, что система станет устойчивой. Практически по диаграмме Боде дефицит устойчивости по модулю оценивается следующим образом (если охватов против часовой стрелки нет, и разомкнутая система устойчива). Ищутся все частоты k, на которых фаза равна -180 , и производная фазы по частоте отрицательна. Определяется максимальная магнитуда на этих частотах. Она и равна дефициту устойчивости. Запас устойчивости – величина, противоположная дефициту. Запас и дефицит устойчивости по модулю измеряются в логарифмических единицах – децибелах и неперах. По диаграмме Боде можно оценить запас устойчивости по фазе. При тех же условиях ищутся все частоты k, на которых магнитуда равна 0 д. Б, и производная фазы по частоте отрицательна. Определяется минимальная фаза min на этих частотах.

Запас устойчивости по фазе определяется как min + 180. Дефицит устойчивости – величина противоположная запасу. У устойчивой системы запас по фазе положителен. Он измеряется в угловых единицах (радианы, градусы и др. ). Определение запасов и дефицитов устойчивости по диаграмме Боде существенно облегчает задачу синтеза корректирующих устройств, входящих в состав регуляторов систем автоматики. Краткие сведения о качестве регулирования Для оценки качества регулирования в САР и САУ применяются различные показатели, связанные с ошибкой регулирования. К этим показателям относятся: 1. параметры переходного процесса при воздействии тестовых входных сигналов; 2. коэффициенты ошибок в установившихся режимах при воздействии тестовых входных сигналов; 3. интегральные показатели оценки качества. В качестве детерминированных тестовых управляющих и возмущающих сигналов обычно используют ступенчатый u(t) = A 1(t), линейный u(t) = A t 1(t) и параболический u(t) = A t 2 1(t). Рассмотрим некоторые параметры переходного процесса системы, структурная схема которой изображена на рисунке, при воздействии ступенчатого входного сигнала 1(t).
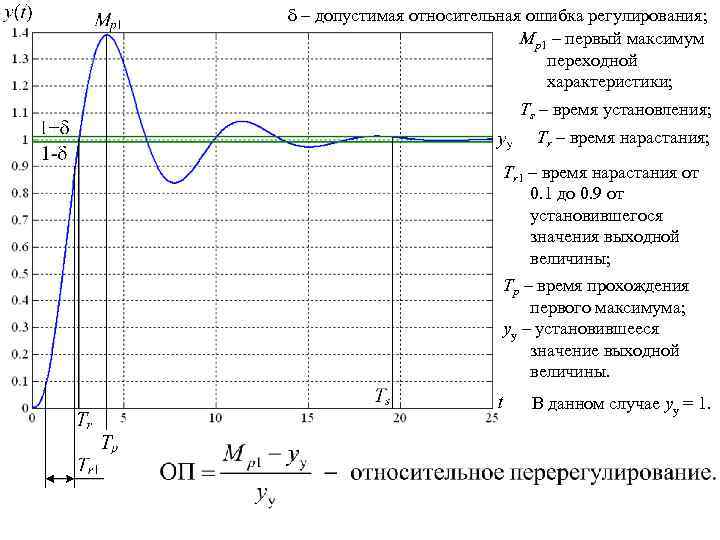
– допустимая относительная ошибка регулирования; Mp 1 – первый максимум переходной характеристики; Ts – время установления; Tr – время нарастания; Tr 1 – время нарастания от 0. 1 до 0. 9 от установившегося значения выходной величины; Tp – время прохождения первого максимума; yy – установившееся значение выходной величины. В данном случае yy = 1.

Ошибка регулирования и коэффициенты ошибок в установившихся режимах Пусть структурная схема замкнутой системы имеет вид Пусть входной сигнал представляет собой единичную ступенчатую функцию u(t) = 1(t). Тогда установившаяся ошибка _______ Отношение этой ошибки к установившемуся значению входного сигнала называют коэффициентом ошибки по положению (в этом случае k 0 = ess). Если входной сигнал представляет собой линейную функцию u(t) = A t 1(t), то установившаяся ошибка равна Отношение этой ошибки к установившейся скорости изменения входного сигнала называют коэффициентом ошибки по скорости k 1 = ess/A.

Если входной сигнал представляет собой параболическую функцию u(t) = a t 2 1(t)/2, то установившаяся ошибка равна ____ Отношение этой ошибки к установившемуся ускорению изменения входного сигнала называют коэффициентом ошибки по ускорению k 2 = ess/a. Требования к снижению коэффициентов ошибок, как правило, вступают в противоречие с требованием обеспечения устойчивости САР и САУ. Как правило, для снижения коэффициентов ошибок требуется увеличение статического коэффициента передачи разомкнутой системы. А с соответствии с критерием устойчивости Найквиста увеличение этого коэффициента способствует появлению дополнительных охватов по часовой стрелке диаграммой Найквиста точки -1 на комплексной плоскости. Интегральные показатели оценки качества Количественная интегральная оценка качества крайне важна для работы адаптивных систем управления, для автоматической оптимизации параметров систем управления и для синтеза оптимальных систем. Оценка качества – это численный показатель качества системы, который выбирается так, чтобы подчеркнуть наиболее важное требование, предъявляемое к системе. Система считается оптимальной системой управления, если её параметры выбраны таким образом, что оценка качества принимает экстремальное (обычно минимальное) значение. Чтобы оценка качества имела реальный смысл, она должна представлять собой число, которое всегда положительно или равно нулю. Тогда наилучшей системой будет та, в которой эта оценка имеет минимальное значение. В практике проектирования систем автоматики обычно применяется один из следующих четырёх интегральных показателей оценки качества:

Верхний предел интегрирования T выбирается достаточно произвольно, но так, чтобы интеграл стремился к конечному значению. Обычно удобно выбирать T равным времени установления Ts. Перечисленные четыре показателя являются абсолютными интегральными показателями качества. Вместо них могут применяться относительные интегральные оценки качества:

Последние четыре показателя являются безразмерными и могут выражаться в процентах. Раздел 3 Типовые динамические звенья Пропорциональное (безынерционное) звено На структурной схеме оно обозначается прямоугольником, внутри которого записывается коэффициент передачи, например, K. Комплексная частотная характеристика: H(j ) = K. АЧХ такого звена – постоянная функция, не зависящая от частоты: H( ) = |K|. ФЧХ: ( ) = 0, если K>0, и ( ) = , если K<0. Импульсная характеристика: h(t) = K (t), т. е. представляет собой -функцию. Переходная характеристика: g(t) = K 1(t).
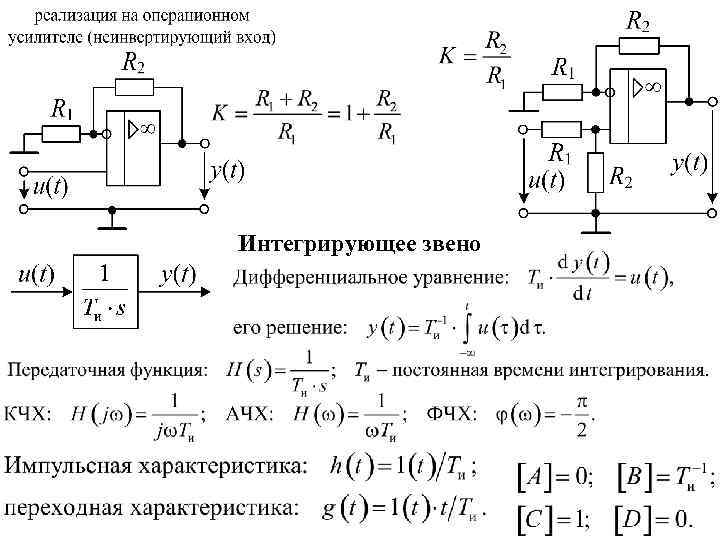
Интегрирующее звено

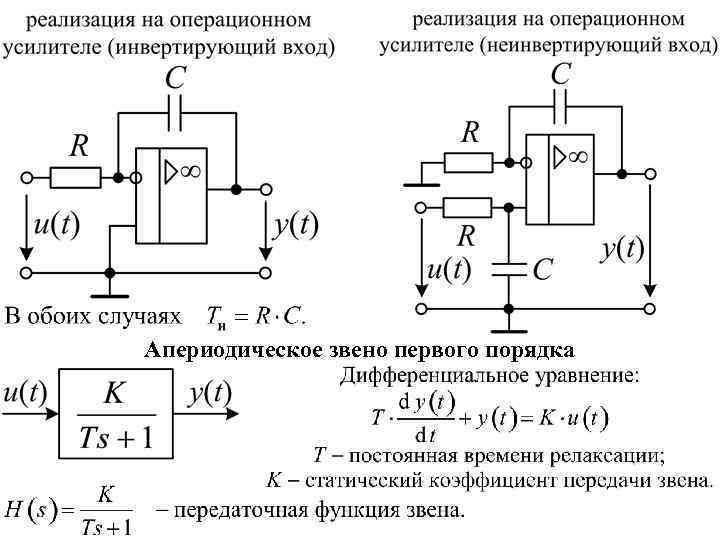
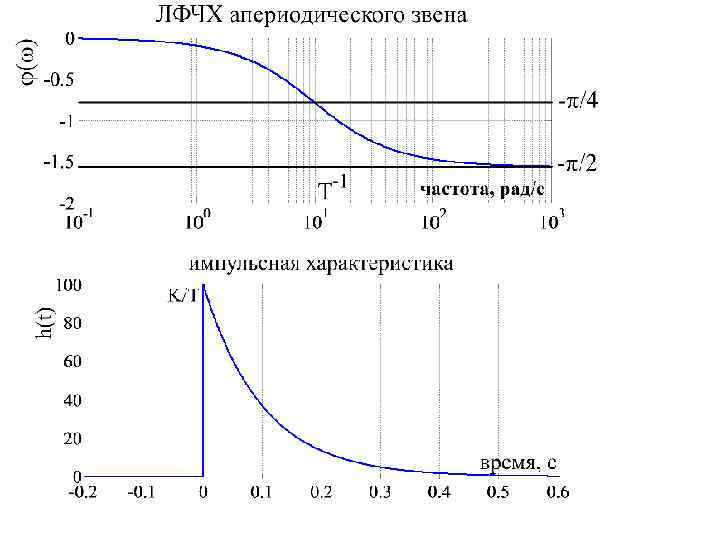
Апериодическое звено первого порядка

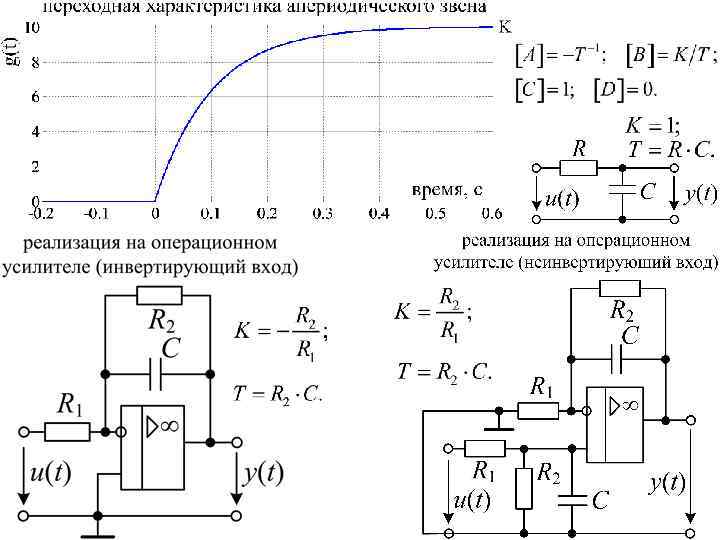
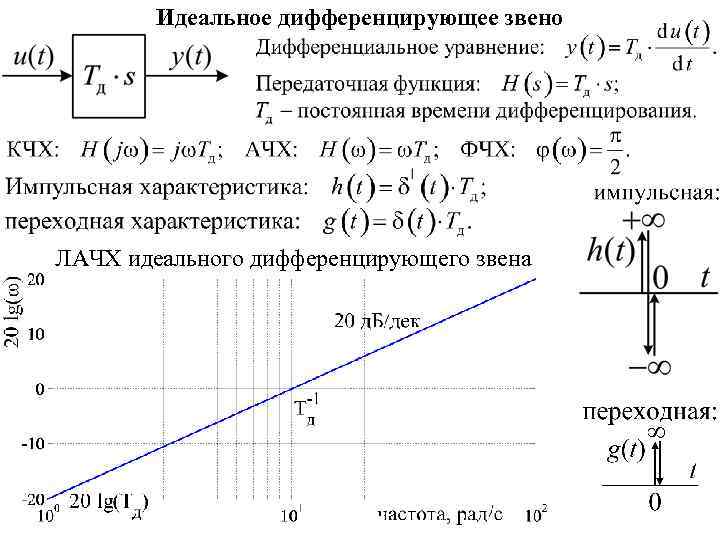
Идеальное дифференцирующее звено ЛАЧХ идеального дифференцирующего звена

Идеальное дифференцирующее звено не является устойчивым в смысле «ограниченный вход – ограниченный выход» , т. к. при стремлении частоты к бесконечности модуль коэффициента передачи стремится к бесконечности. Поэтому из-за неидеальности динамических свойств самого операционного усилителя каскады, изображённые на схемах, самовозбуждаются на высоких частотах и работают в режиме автоколебаний. «Реальное» дифференцирующее звено Это звено можно считать эквивалентом каскадного соединения идеального дифференцирующего звена и апериодического звена первого порядка.
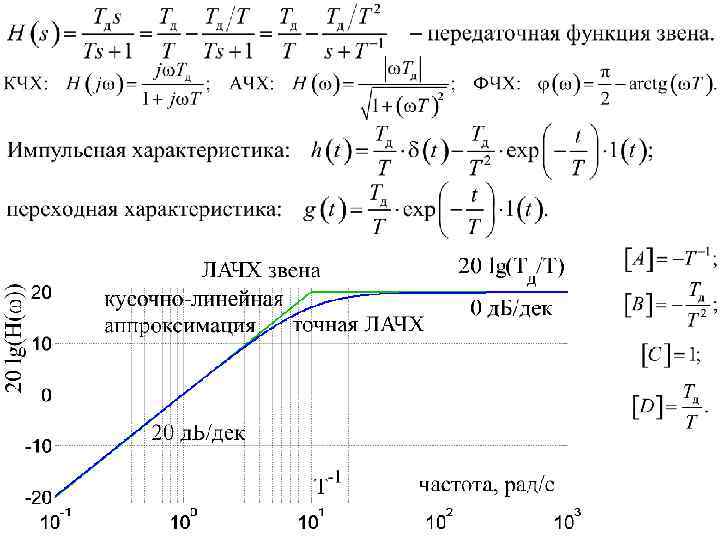
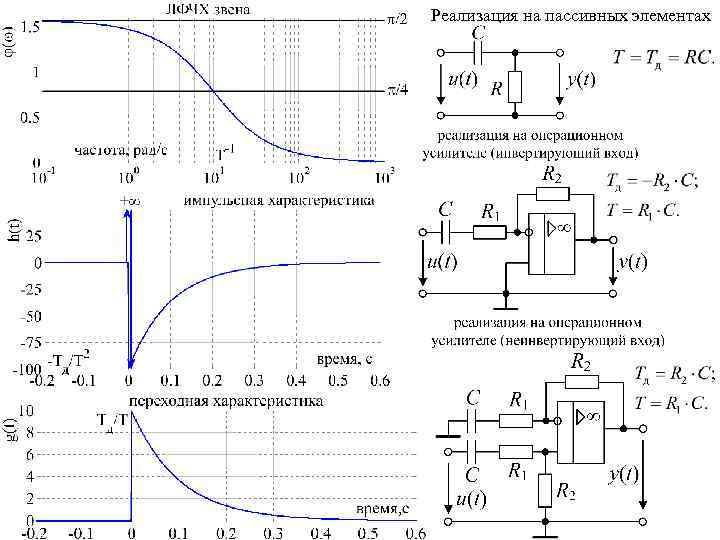
Реализация на пассивных элементах

Апериодическое звено второго порядка Это звено можно считать эквивалентом каскадного соединения двух апериодических звеньев первого порядка.
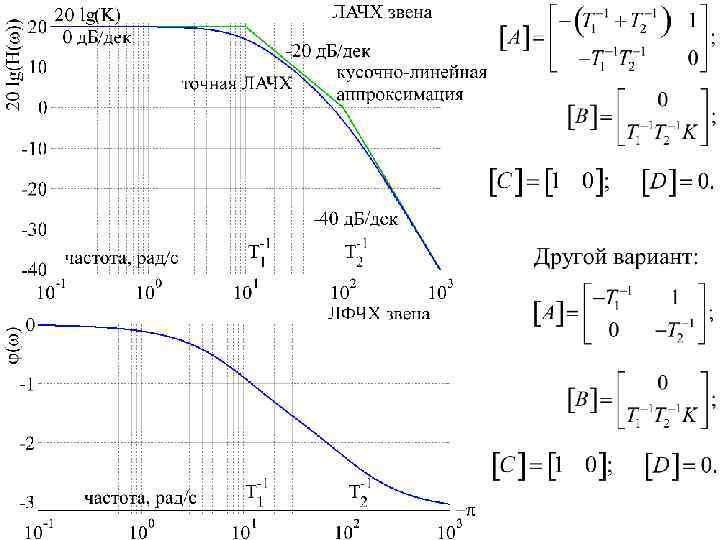

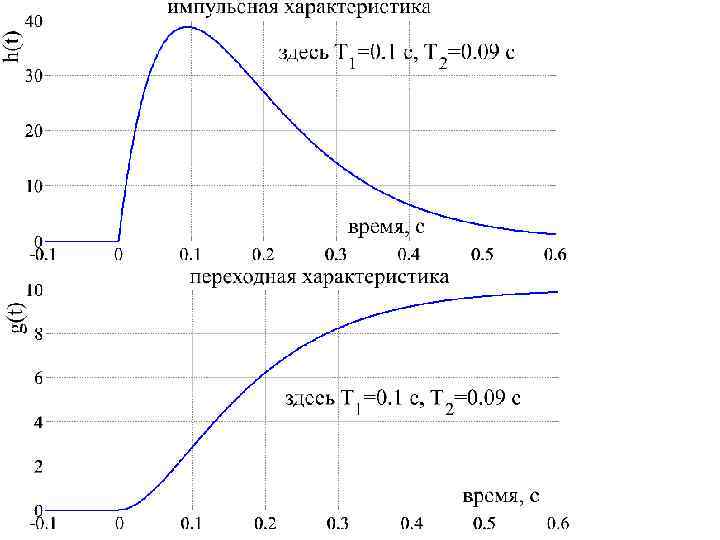

Колебательное и консервативное звено Импульсная характеристика такого звена представляет собой экспоненциально затухающую синусоидальную функцию времени. Передаточная функция имеет второй порядок. K – статический коэффициент передачи сигнала; T – постоянная времени колебательного звена; – коэффициент демпфирования. При =0 звено называется консервативным. Импульсная характеристика такого звена представляет собой незатухающую синусоидальную функцию времени. При 1 колебательное звено становится апериодическим звеном второго порядка.

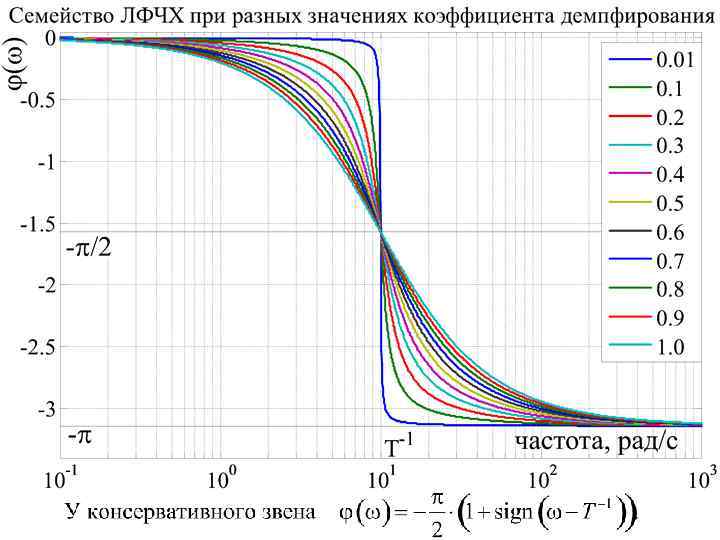
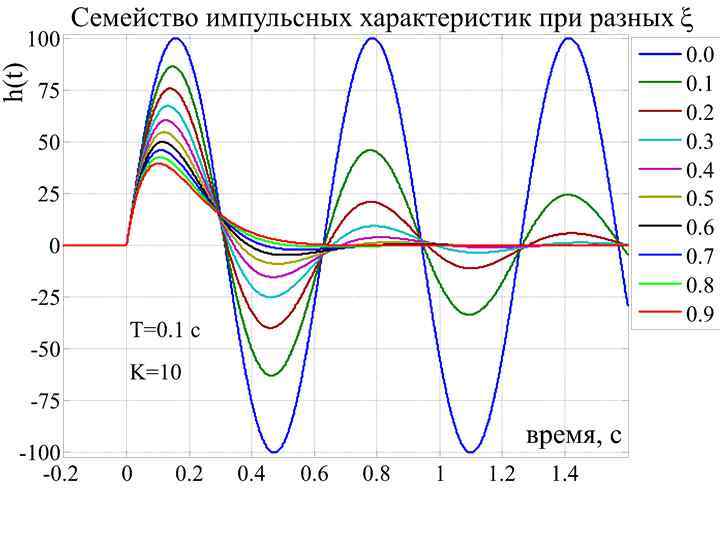
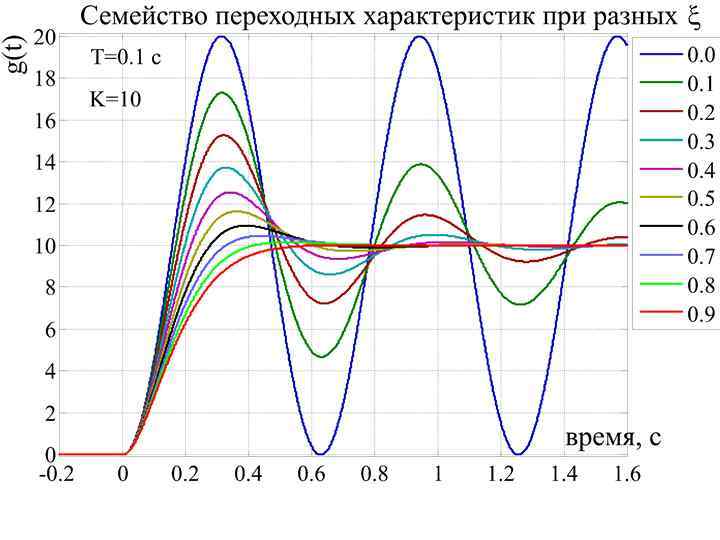

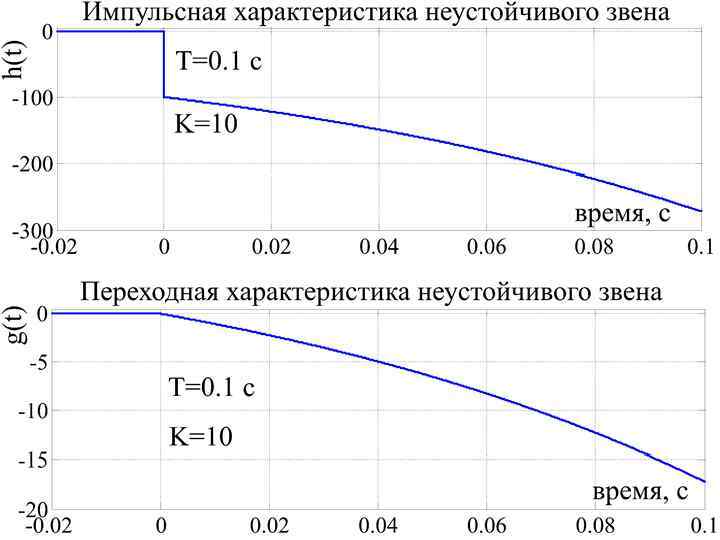
Динамические свойства колебательного звена в пространстве состояний Неустойчивое звено первого порядка
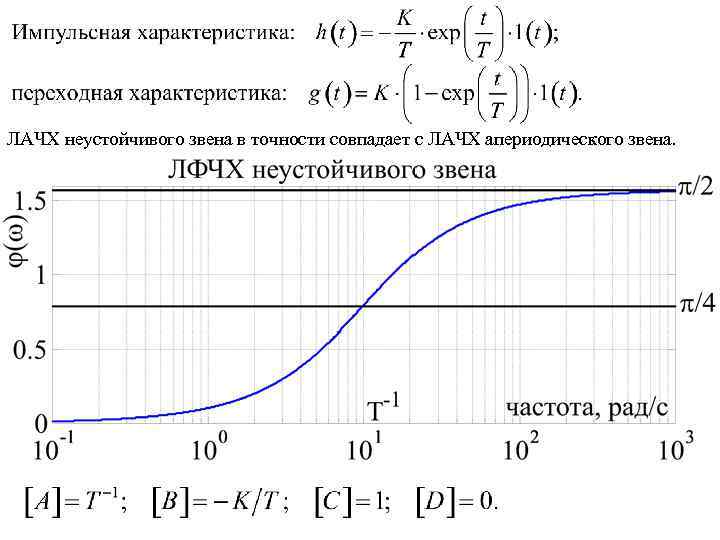
ЛАЧХ неустойчивого звена в точности совпадает с ЛАЧХ апериодического звена.

Запаздывающее звено не искажает входной сигнал, т. к. модуль коэффициента передачи не зависит от частоты, а аргумент коэффициента передачи прямо пропорционален частоте.
Устойчивость СЭ, лекции.ppt