d76252b226125ba7e6c42311c740493c.ppt
- Количество слайдов: 95

Special Probability Distributions Schaum’s Outline Probability and Statistics Chapter 4 Presented by Carol Dahl 1

4 -2 Chapter 4 Outline Ø Binomial Distribution Ø Normal Distribution Ø Poisson Distribution Ø Relations Between Distributions Binomial and Normal Binomial and Poisson and Normal Ø Central Limit Theorem

4 -3 Outline Ø Multinomial Distribution Ø Hypergeometric Distribution Ø Uniform Distribution Ø 2 Distribution Ø t-Distribution Ø F-Distribution Ø Cauchy Ø Exponential Ø Lognormal

4 -4 Introduction Special Probability Distributions give probabilities for random variables discrete and continuous help us make inferences

4 -5 Distributions Help Make Inferences Powerful tools - uncertainty prediction confidence intervals Q = ßo + ß 1 P + ß 2 Y hypothesis tests

4 -6 Binomial Distribution You own ten draglines for mining coal

4 -7 Binomial (Bernoulli) Distribution Probability associated with no repairs P(no repairs) = p P(repairs) = (1 -p) = q If breakdown between machines independent Bernoulli Trial n trials = 10 x number with no repairs out of n draglines Binomial distribution P(X=x)= n pxqn-x=n!/(x!(n-x)!)pxqn-x x

4 -8 Binomial Example Dragline P(repairs) = 0. 2 Binomial P(X=x) = ( n ) px(1 -p)n-x ( x ) P(X=2) = (10) 0. 22 (1 -0. 2)10 -2 = 10! 0. 22*0. 88 2 2!(10 -2)! = 0. 302 Excel insert, function, statistical, binomdist =binomdist(x, n, p, cumulative) (true or false) = binomdist(2, 10, 0. 2, false)
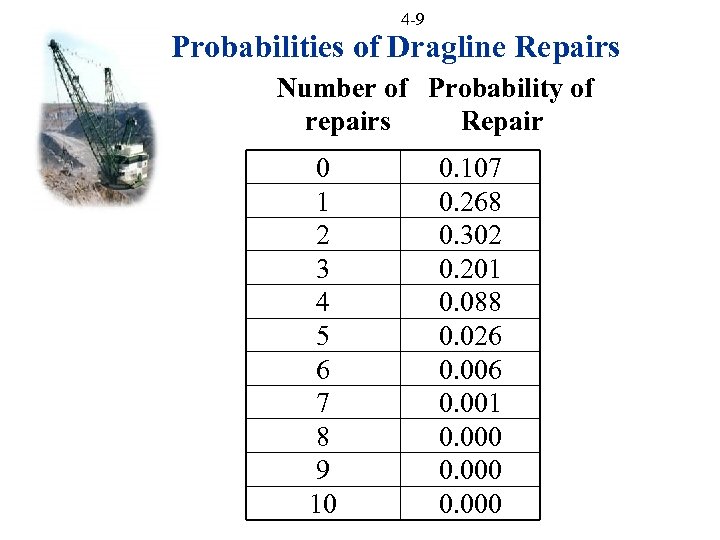
4 -9 Probabilities of Dragline Repairs Number of Probability of repairs Repair 0 1 2 3 4 5 6 7 8 9 10 0. 107 0. 268 0. 302 0. 201 0. 088 0. 026 0. 001 0. 000

4 -10 Probabilities of Dragline Repairs

4 -11 Properties of Binomial Distribution Discrete Suppose n = 10, P = 0. 2 Mean =np = 10*0. 2 = 8 Variance 2=npq = 10*0. 2*0. 8 = 1. 6 Standard deviation = (1. 6 )0. 5 = 1. 265 Coefficient of skewness α 3=(q-p)/ = (0. 8 – 0. 2)/ 1. 265 = 0. 474 Coefficient of kurtosis α 4=3+(1 -6 pq)/npq = 3 + (1 -6*0. 8*0. 2)/1. 6 = 3. 025

4 -12 Functions Relating to Binomial Moment generating function M(t)=(q+pet)n M(t) = E(et. X) = xet. XP(X) E(X) = x. XP(X) = M'(0) M'(t)=n(q+pet)n-1 pet M'(0)=n(q+pe 0)n-1 pe 0 = n((1 -p)+p)n-1 p =np E(X 2) = x. X 2 P(X) = M''(0) E(X 3) = x. X 3 P(X) = M'''(0) Replacing t by iω with i imaginary number (-1)0. 5 then we get another useful function Characteristic function φ(ω)=(q+peiω)n

4 -13 Law of Large Numbers for Bernouilly Trials Estimate p by sampling p = x/n By increasing number of trials can get as close as we want to true mean lim P (|X/n – p|>ε) = 0 n->
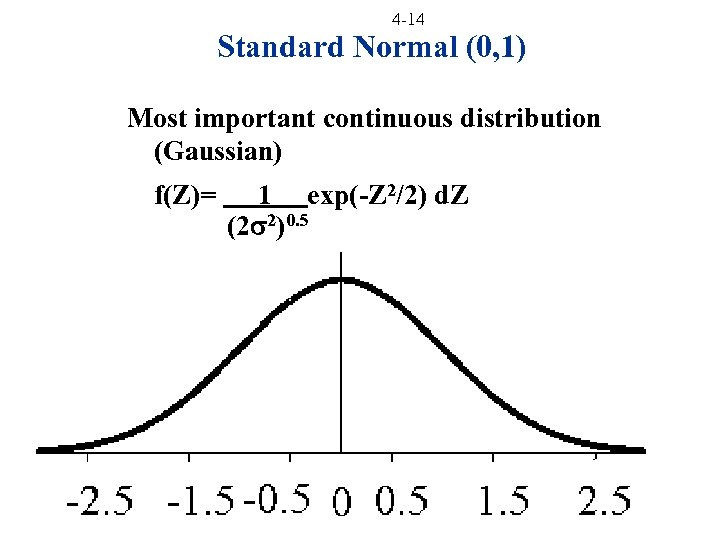
4 -14 Standard Normal (0, 1) Most important continuous distribution (Gaussian) f(Z)= 1 exp(-Z 2/2) d. Z (2 2)0. 5

4 -15 Standard Normal (0, 1) Example Building a hydro – Three Gorges – 18, 000 MW

4 -16 Standard Normal (0, 1) Want to know how much rainfall deviated from normal Z Z ~ N(0, 1) with Z measured in inches Five things you might want to know P(Z < a) P(Z > b) P(Z < -c) P(Z > -d) P(e < Z < f)
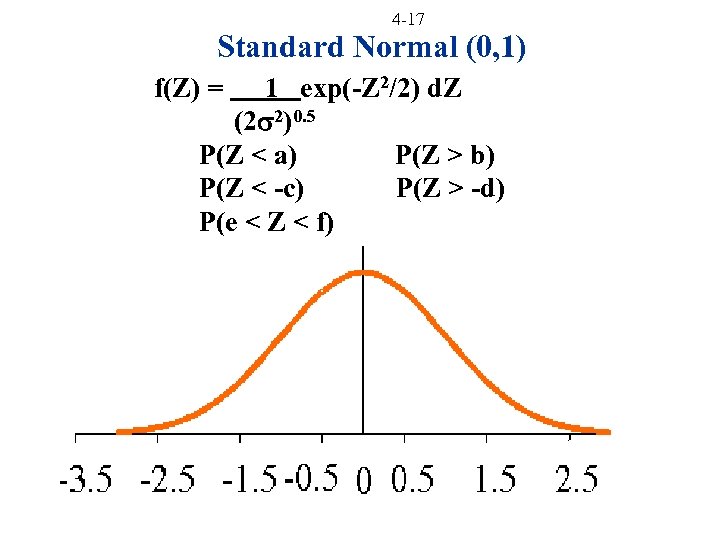
4 -17 Standard Normal (0, 1) f(Z) = 1 exp(-Z 2/2) d. Z (2 2)0. 5 P(Z < a) P(Z > b) P(Z < -c) P(Z > -d) P(e < Z < f)

4 -18 Standard Normal (0, 1) a P(Z < a) = 1 exp(-Z 2/2) d. Z (2 )0. 5 - P(Z > b) = 1 exp(-Z 2/2) d. Z (2 )0. 5 b P(Z < -c) = 1 -cexp(-Z 2/2) d. Z (2 )0. 5 - P(Z > -d) = 1 exp(-Z 2/2) d. Z (2 )0. 5 -d f P(e < Z < f) = 1 exp(-Z 2/2) d. Z 0. 5 e (2 ) P(e < Z < f) = P(Z <f) – P(Z < e)
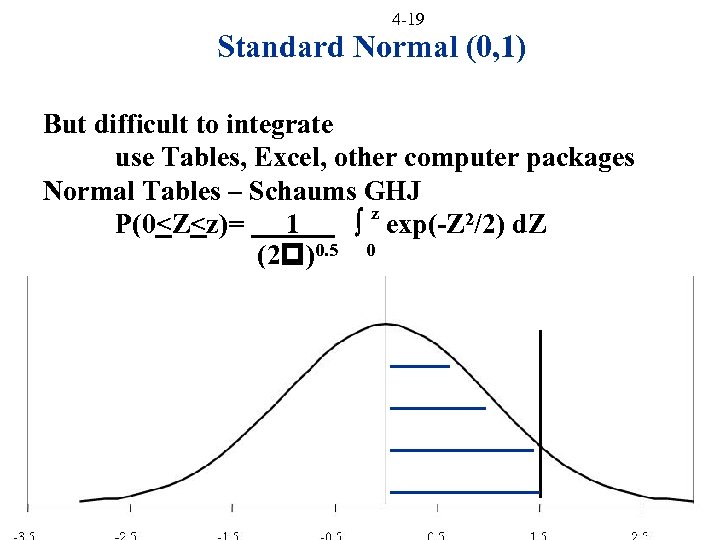
4 -19 Standard Normal (0, 1) But difficult to integrate use Tables, Excel, other computer packages Normal Tables – Schaums GHJ z P(0<Z<z)= 1 exp(-Z 2/2) d. Z (2 )0. 5 0
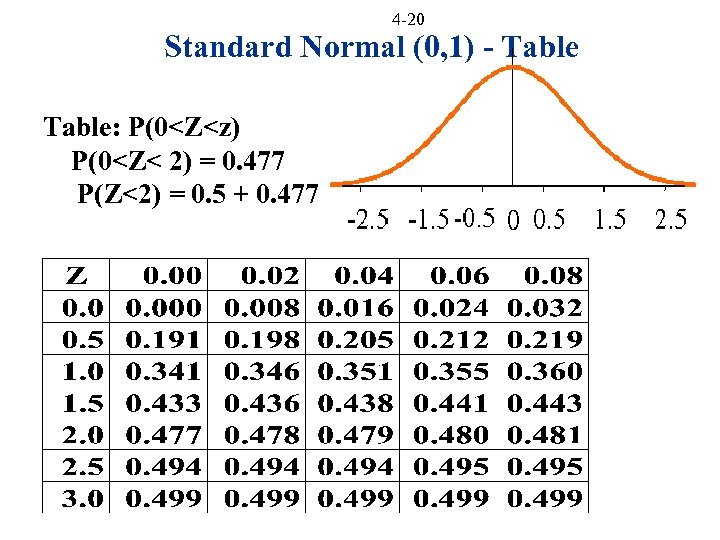
4 -20 Standard Normal (0, 1) - Table: P(0<Z<z) P(0<Z< 2) = 0. 477 P(Z<2) = 0. 5 + 0. 477
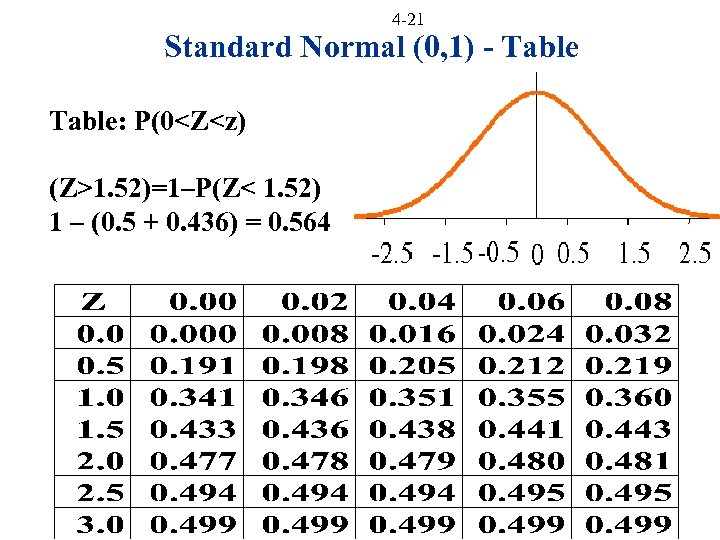
4 -21 Standard Normal (0, 1) - Table: P(0<Z<z) (Z>1. 52)=1–P(Z< 1. 52) 1 – (0. 5 + 0. 436) = 0. 564
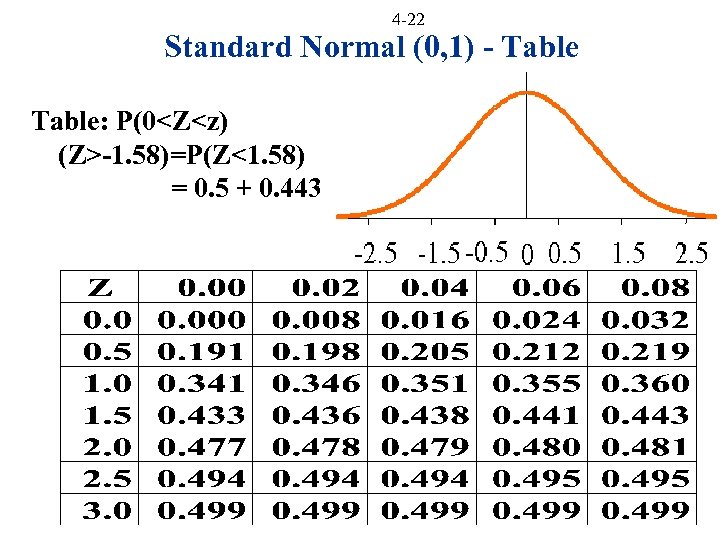
4 -22 Standard Normal (0, 1) - Table: P(0<Z<z) (Z>-1. 58)=P(Z<1. 58) = 0. 5 + 0. 443
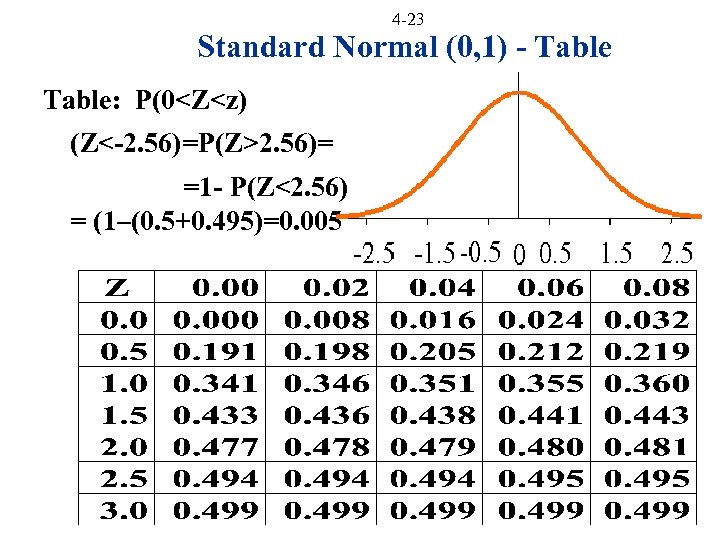
4 -23 Standard Normal (0, 1) - Table: P(0<Z<z) (Z<-2. 56)=P(Z>2. 56)= =1 - P(Z<2. 56) = (1–(0. 5+0. 495)=0. 005
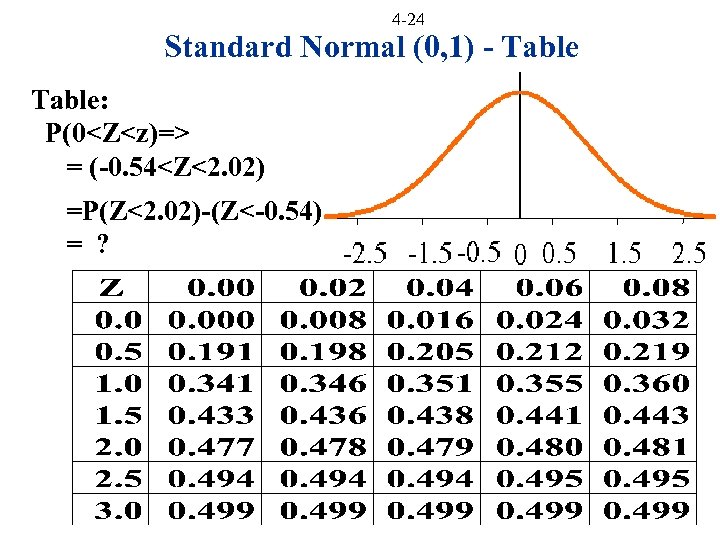
4 -24 Standard Normal (0, 1) - Table: P(0<Z<z)=> = (-0. 54<Z<2. 02) =P(Z<2. 02)-(Z<-0. 54) = ?
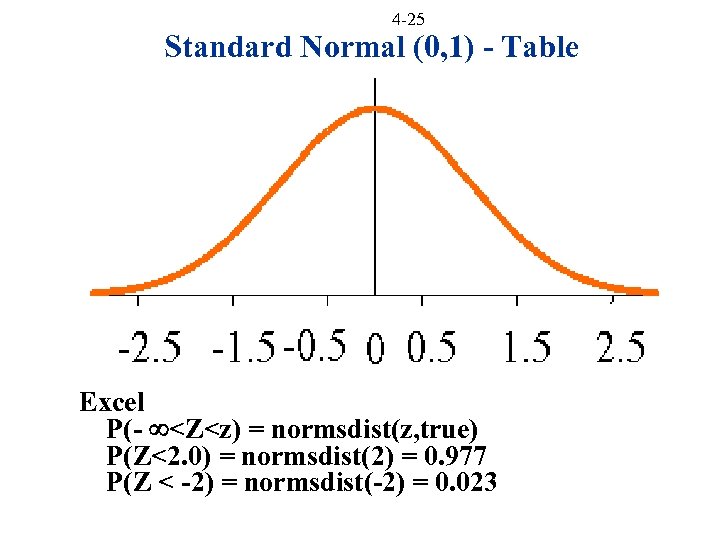
4 -25 Standard Normal (0, 1) - Table Excel P(- <Z<z) = normsdist(z, true) P(Z<2. 0) = normsdist(2) = 0. 977 P(Z < -2) = normsdist(-2) = 0. 023
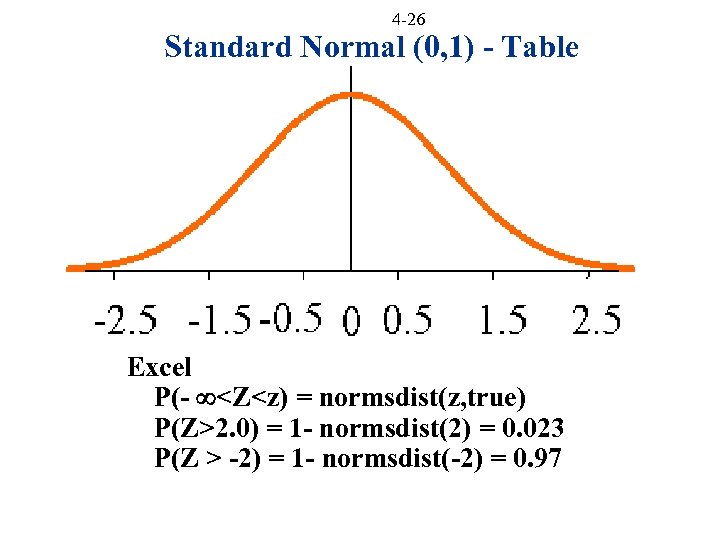
4 -26 Standard Normal (0, 1) - Table Excel P(- <Z<z) = normsdist(z, true) P(Z>2. 0) = 1 - normsdist(2) = 0. 023 P(Z > -2) = 1 - normsdist(-2) = 0. 97

4 -27 Inverse Normal: P(Z<1) = Deviation in rainfall < 1 inch above normal what % of the time? P(Z<-1. 5) = Deviation in rainfall < 1. 5 inch below normal what % of the time? Inverse Normal P(Z<z) = 0. 05 Rain fall deviates < what amount 5% of the time
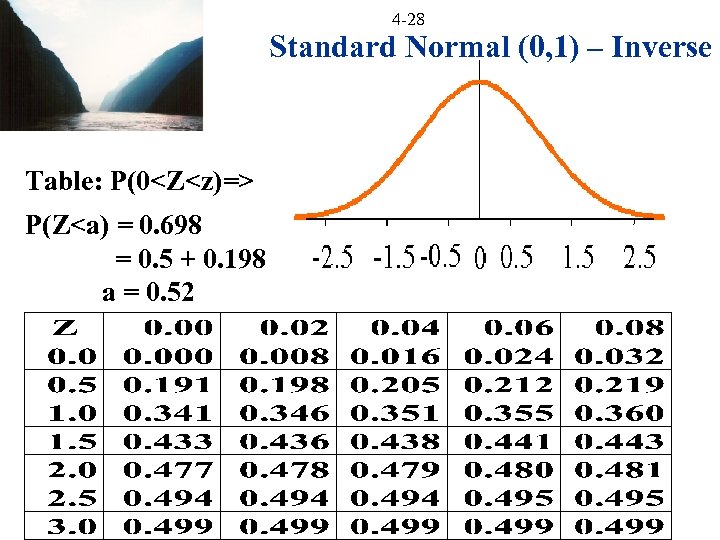
4 -28 Standard Normal (0, 1) – Inverse Table: P(0<Z<z)=> P(Z<a) = 0. 698 = 0. 5 + 0. 198 a = 0. 52
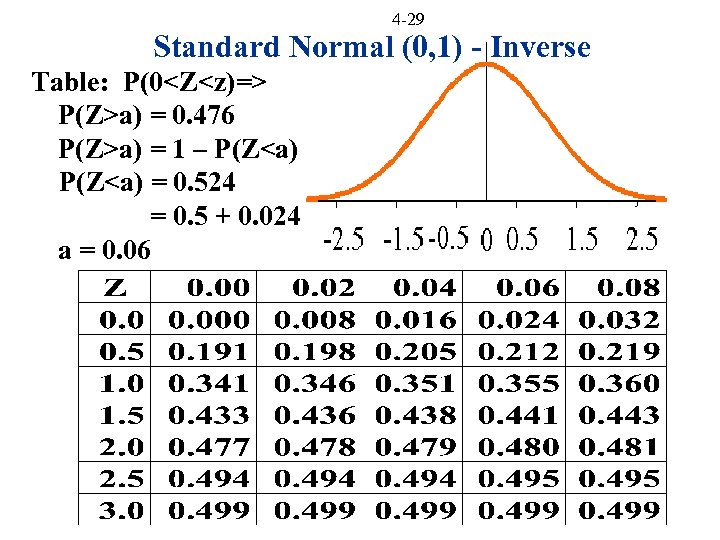
4 -29 Standard Normal (0, 1) - Inverse Table: P(0<Z<z)=> P(Z>a) = 0. 476 P(Z>a) = 1 – P(Z<a) = 0. 524 = 0. 5 + 0. 024 a = 0. 06
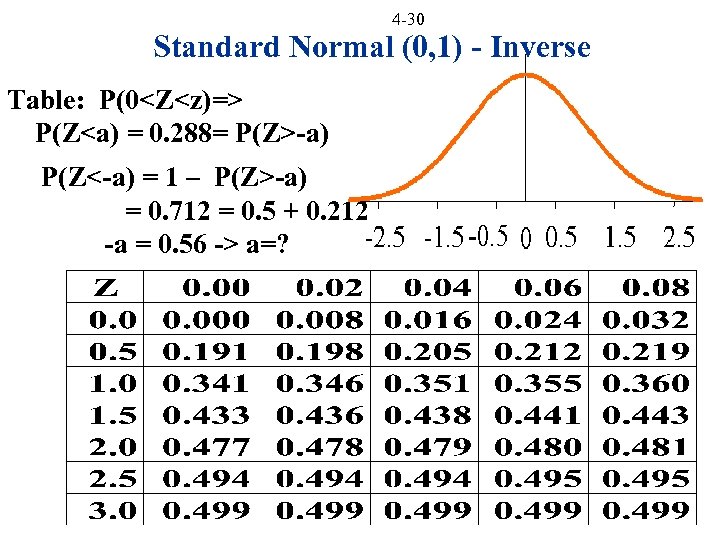
4 -30 Standard Normal (0, 1) - Inverse Table: P(0<Z<z)=> P(Z<a) = 0. 288= P(Z>-a) P(Z<-a) = 1 – P(Z>-a) = 0. 712 = 0. 5 + 0. 212 -a = 0. 56 -> a=?
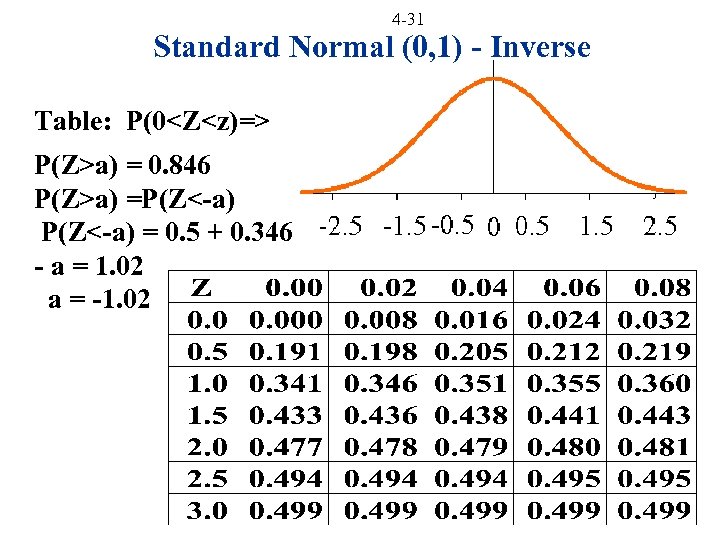
4 -31 Standard Normal (0, 1) - Inverse Table: P(0<Z<z)=> P(Z>a) = 0. 846 P(Z>a) =P(Z<-a) = 0. 5 + 0. 346 - a = 1. 02 a = -1. 02
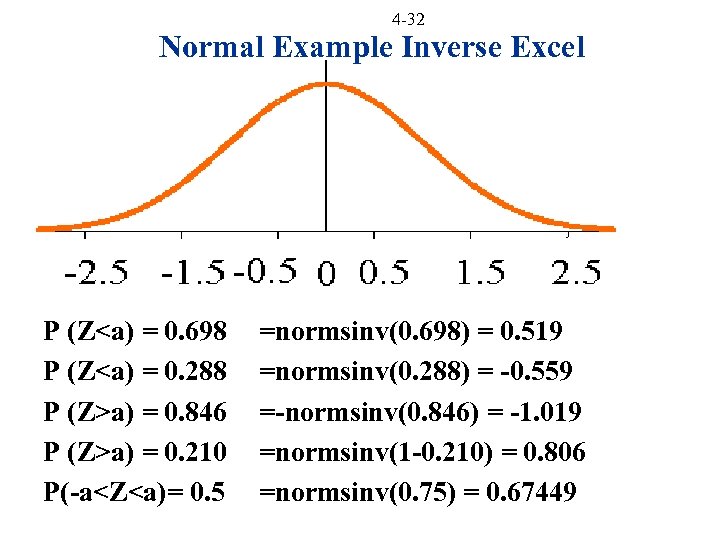
4 -32 Normal Example Inverse Excel P (Z<a) = 0. 698 P (Z<a) = 0. 288 P (Z>a) = 0. 846 P (Z>a) = 0. 210 P(-a<Z<a)= 0. 5 =normsinv(0. 698) = 0. 519 =normsinv(0. 288) = -0. 559 =-normsinv(0. 846) = -1. 019 =normsinv(1 -0. 210) = 0. 806 =normsinv(0. 75) = 0. 67449

4 -33 Properties of Normal Distribution Mean Variance 2 Standard deviation Coefficient of skewness 3=0 Coefficient of kurtosis 4=3 Moment generating function M(t)=e t+( ^2*t^2/2) Characteristic function ( )=ei -( ^2 ^2/2)

4 -34 Relation between Distributions Binomial => Normal n gets large

4 -35 Poisson Distribution Discrete infinite distribution with pdf f(x)=P(X=x)= xe- /x! x=0, 1, 2, 3, . . . = mean decay radioactive particles demands for services demands for repairs

4 -36 Poisson Distribution Example: X number of well workovers/month X ~ poisson mean = 5 P(X = 3) = 53 e-5 = 0. 140 5!

4 -37 Poisson Distribution in Excel = poisson(x, (mean), cumulative) true or false P(X = 3) = poisson(3, 5, false) = 0. 14 P(X< 3) = poisson(3, 5, true) = 0. 265 p(X > 8) = 1 - poisson(7, 5, true) = 0. 13

4 -38 Properties of Poisson Mean = Variance 2 = Standard deviation = 1/2 Coefficient of skewness 3= -1/2 Coefficient of kurtosis 4= 3 + 1/ Moment generating function M(t)=e (e^t-1) Characteristic function ( )=e (e^(i )-1)

4 -39 Relations between Distributions Poisson and Binomial close when n large & p small Poisson and Normal are close when n gets large To standardize Poisson Z = (X - )/ 0. 5

4 -40 Central Limit Theorem random variables X 1, X 2, … independent identically distributed finite mean and variance 2. then X = (X 1 + X 2 +…+Xn)/n goes to a N( , 2/n) as n ->

4 -41 Multinomial Distribution Example: You work for a gas company likelihood a family will buy gas furnace is 1/2 (p 1) electric furnace is 1/3 (p 2) fuel oil furnace is 1/6 (p 3) 10 furnaces (n) replaced in next heating season probability that 5 (x 1) gas? 4 (x 2) electric 1 (x 3) fuel oil?

4 -42 Multinomial Distribution Generalization of binomial A 1, A 2, A 3, …Ak are events occur with probabilities p 1, p 2, …pk If X 1, X 2, …Xk are random variables number of times that A 1, A 2, …Ak occur n trials X 1 + X 2+…+Xk = n then P(X 1 = n 1, X 2 = n 2, …, nk) = n! p 1 n 1 p 2 n 2…pknk n 1! n 2!…nk! Where n 1 + n 2+…, + nk = n

4 -43 Multinomial Distribution Work out probability for 5 (x 1) gas? 4 (x 2) electric 1 (x 3) fuel oil? P(x 1=5, x 2=4, x 3=1) =

4 -44 Hypergeometric Distribution Example: Box of drilling bits contains 5 “X” bit 4 “+” bit 3 “button” bit 6 bits selected at random from box no replacement Find probability: 3 are “X” bits, 2 are “+” bits and 1 is “button” bits

4 -45 Hypergeometric Distribution Probability P(choose x 1 from n 1, x 2 from n 2, etc

4 -46 Hypergeometric Distribution Excel Example: Box contains 6 assays of copper 4 assays of gold choose an essay at random no replacement 5 trials X = number of copper essays chosen P(X=3) Use hypergeometric

4 -47 Hypergeometric Distribution Excel We are choosing from two categories - copper (s) and gold (not s) X - number of copper assays chosen number in s = ns = 6, number in not s = nns= 4 total population = ns+nns = 6 + 4 = 10 sample size = n = 5 =hypgeomdist(x, n, ns+nns) = P(X<x). P(X=3) = hypgeomdist(3, 5, 6, 10) - hypgeomdist(2, 5, 6, 10) = 0. 476

4 -48 Uniform Distribution Random variable X uniformly distributed in a<=x<=b if density functions: 1/(b-a) a<=x<=b f(x) = 0 otherwise

4 -49 Uniform Distribution Example Failure rate on bits X ~ f(x) = 1/2 2 < X < 4 years P (X > 3) = 34(1/2)d. X = 0. 5 X| 34 = 0. 5*4 – 0. 5*3 = 0. 50 half of bits last more than 3 years P (2<X< 2. 5) = 22. 5(1/2)d. X = 0. 5 X| 22. 5 = 0. 5*2. 5 – 0. 5*2 = 0. 25 P(2. 7<X<3. 3) = ?

4 -50 Distributions for Econometric Inference Y = ßo + ß 1 X 1 + ß 2 X 2 + estimate ßs Y^ = bo + b 1 X 1 + b 2 X 2 assumptions about distribution of mean and variance gives us distributions of Y^, bo, b 1 mean and variance
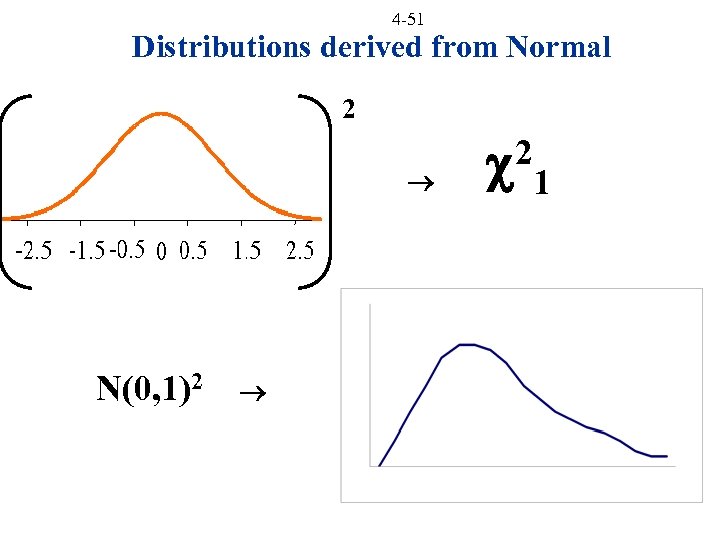
4 -51 Distributions derived from Normal 2 N(0, 1)2 2 1
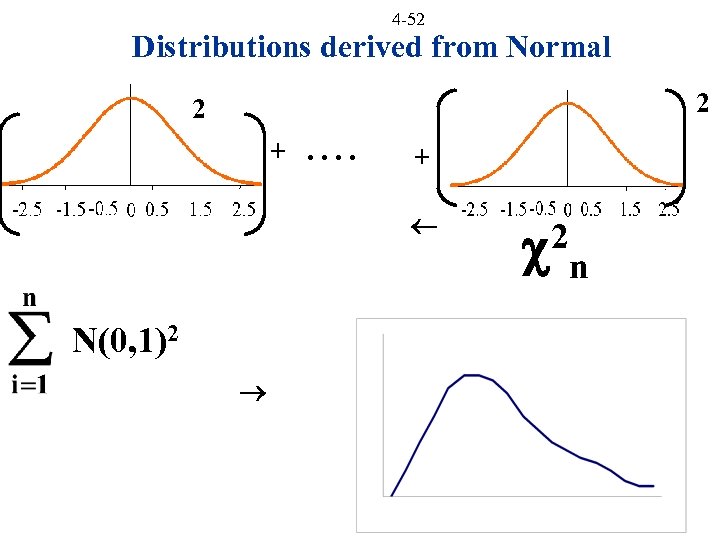
4 -52 Distributions derived from Normal 2 2 + . . + N(0, 1)2 2 n
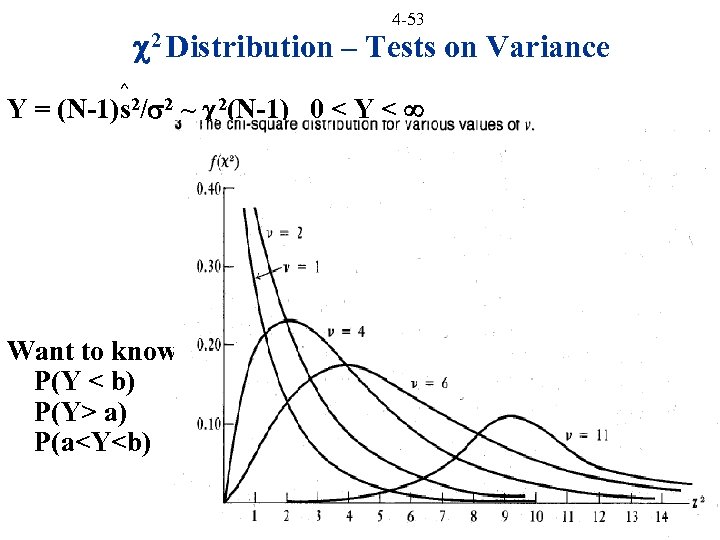
4 -53 2 Distribution – Tests on Variance ^ Y = (N-1)s 2/ 2 ~ 2(N-1) 0 < Y < Want to know P(Y < b) P(Y> a) P(a<Y<b)
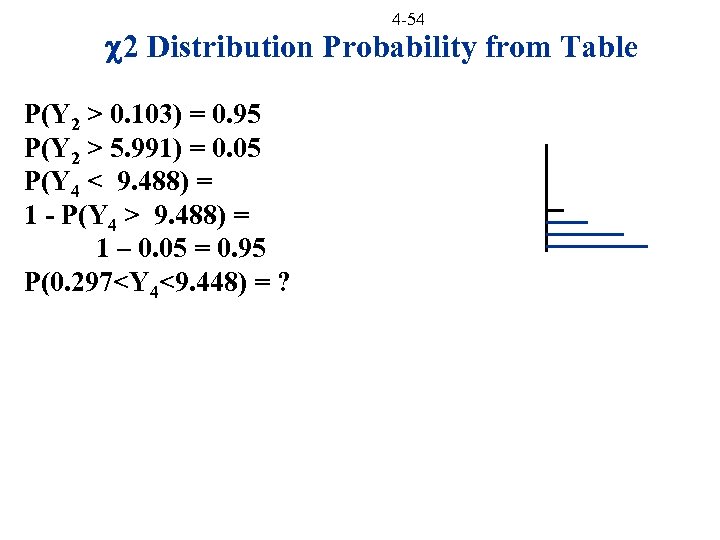
4 -54 2 Distribution Probability from Table P(Y 2 > 0. 103) = 0. 95 P(Y 2 > 5. 991) = 0. 05 P(Y 4 < 9. 488) = 1 - P(Y 4 > 9. 488) = 1 – 0. 05 = 0. 95 P(0. 297<Y 4<9. 448) = ?

4 -55 2 Distribution Inverse Probability from Table P(Y 3 > c) = 0. 95 c = 0. 352 P(Y 4 < c) = 0. 99 1 - P(Y 4 > c) = 1 – 0. 99 = 0. 01 => c = 13. 277

4 -56 2 Distribution Probability from Excel P(Y 5 > c) = chidist(c, 5) = P(Y 5 > 2) = chidist(2, 5) = 0. 849 P(Y 6 < c) = 1 – P(Y 6 > c) = 1 - chidist(c, 6) P(Y 6<4) = 1 - P(Y 6 > 4) = 1 - chidist(4, 6) = 0. 323

4 -57 2 Distribution Inverse Probability from Excel P(Y 3 > c) = => c = chiinv( , 3) P(Y 3 > c) = 0. 05 => c = chiinv(0. 05, 3) = 7. 815 P(Y 6 < c) = P(Y 6 > c) = 1 - => c = chiinv(1 - , 6) P(Y 6<c) = 0. 1 => c = chiinv(0. 90, 6) = 2. 204

4 -58 Distributions for Econometric Inference Y = ßo + ßX 1 + ß 2 X 2 + Y^ = bo + b 1 X 1 + b 2 X 2 assumptions about distribution of = mean E( ) = 0, variance 2 gives us distributions of Y^, bo, b 1, b 2 Each has mean E(Y^), E(bo), E(b 1), E(b 2) Each has variance 2, 2 bo, 2 b 1, 2 b 2 2 tests on variance part of other distributions
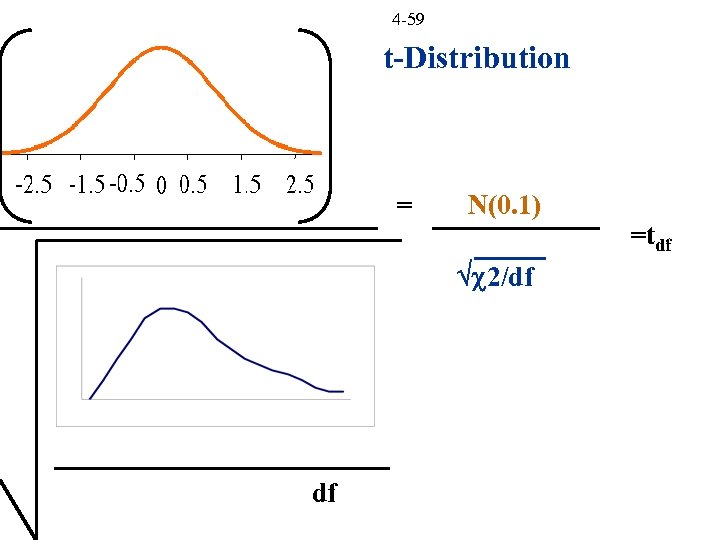
4 -59 t-Distribution = N(0. 1) =tdf 2/df df

4 -60 t-Distribution k degrees of freedom

4 -61 t-Distribution Properties: Ø When df >30 approximates Standard Normal Ø Symmetrical with mean 0 and variance df > 2

4 -62 t-Distribution Uses Used in Econometrics to: ØMake inferences on means ØSimilar to Normal but tables set up differently Ødf bigger the larger the sample Øif n large use normal tables

4 -63 t-Distribution Probabilities Tables P(t 2 > 1. 886) = 0. 10 P(t 4 < 2. 132) = 1 - P(t 4 > 2. 132) = 1 – 0. 05 = 0. 95 P(t 2>-1. 886) = P(t 2<1. 886) = 1 - (t 2>1. 886)= 1 – 0. 10 = 0. 90 P(t 4 < -2. 132) = P(t 4 > 2. 132) = 0. 05 P(1. 638<t 3<3. 182)=?

4 -64 t-Distribution Inverse from Tables P(t 3 > c) = 0. 025 c=3. 182 P(t 4< c) = 0. 90 1 - P(t 4 > c) = 0. 90 P(t 4 > c) = 0. 10 c = 1. 533 P(t 3 > -c) = 0. 975 P(t 3 < c) = 0. 975 = 1 - P(t 3 > c) = 0. 975 P(t 3 > c) = 0. 025 c = 3. 182 P(t 1< -c) = 0. 05 = P(t 1> c) c = 6. 314 P(c 1<t 3<c 2) = 0. 90 ?

4 -65 t-Distribution from Excel P(tdf> c) = = tdist(c, df, 1) = tdist(c, df, 2)/2 P(t 10> 2. 10) = tdist(2. 10, 1) = 0. 031 P(t 20< 1. 86) = 1 - P(t 20>1. 86) = 1 - dist(1. 86, 20, 1) = 0. 961

4 -66 t-Distribution from Excel P(t 15>-1. 56) = P(t 15<1. 56) = 1 - (t 15>1. 56) = 1 – tdist(1. 56, 15, 1) = 0. 93 P(t 12 < -2. 132) = P(t 12 > 2. 132) = tdist(2. 132, 1)= 0. 027 P(c 1<t 3<c 2)= 0. 99 ?

4 -67 t-Distribution Inverse from Excel P(tdf > c) = c=tinv( *2, df 1) P(t 10 > c) = 0. 15 c = tinv(0. 15*2, 10) = 1. 093 P(t 25< c) = 0. 90 1 - P(t 25> c) = 0. 90 P(t 25>c) = 0. 10 c= tinv(0. 10*2, 25) c = 1. 316

4 -68 t-Distribution Inverse from Excel P(t 3 > -c) = 0. 975 P(t 3 < c) = 0. 975 = 1 - P(t 3 > c) = 0. 025 c = tinv(0. 025*2, 3) c = 3. 182 P(t 1< -c) = 0. 05 = P(t 1> c) c =tinv(0. 05*2, 1)=6. 314 P(c 1<t 17<c 2) = 0. 90 ?
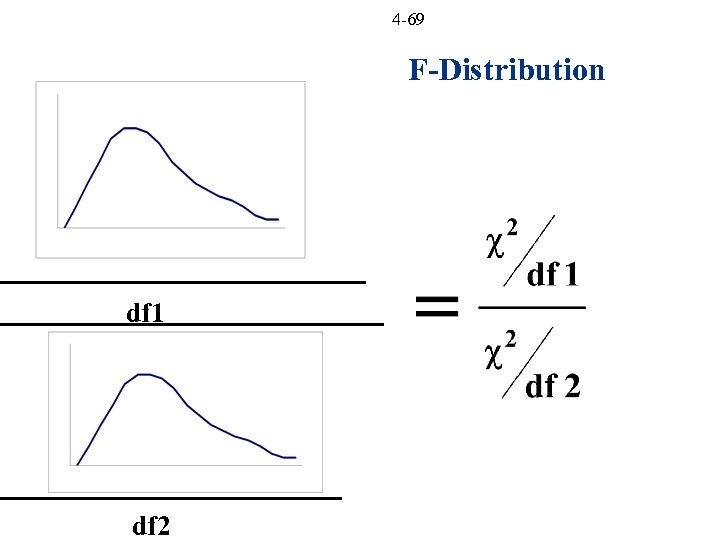
4 -69 F-Distribution df 1 df 2
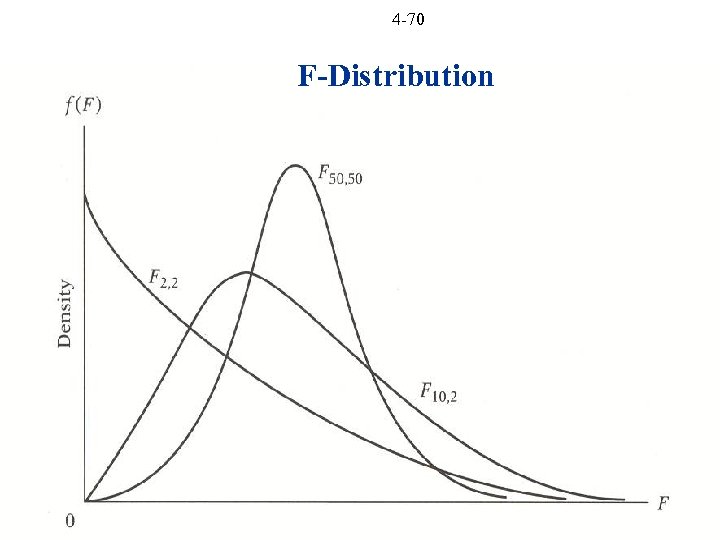
4 -70 F-Distribution

4 -71 F-Distribution Used in Econometrics to: Test between Øtwo variances Øseveral means Øsubset ’s not simultaneously = 0 Comes from 2 so 0<F

4 -72 F-Distribution Relation to Other Distributions If k 2 (denominator df) is large

4 -73 F-Distribution Properties: k 1 = numerator df; k 2 = denominator df Skewed to right approaches N(0, 1) as k 1 and k 2 get larger Mean = k 2 > 2 Variance = k 2 > 4
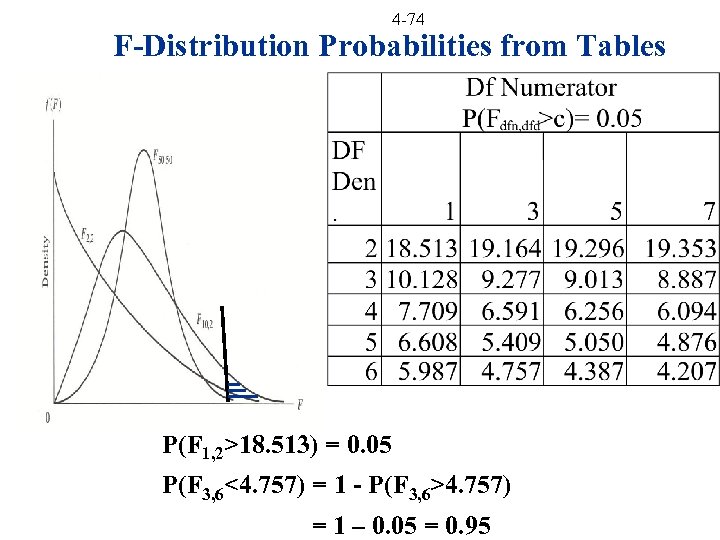
4 -74 F-Distribution Probabilities from Tables P(F 1, 2>18. 513) = 0. 05 P(F 3, 6<4. 757) = 1 - P(F 3, 6>4. 757) = 1 – 0. 05 = 0. 95
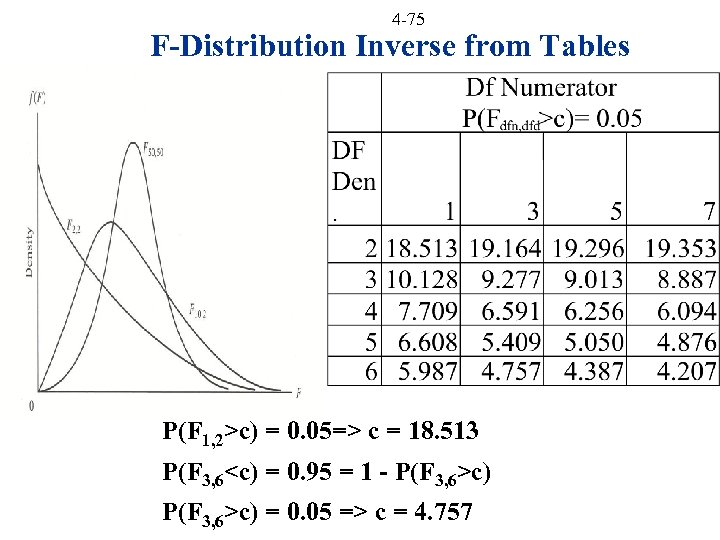
4 -75 F-Distribution Inverse from Tables P(F 1, 2>c) = 0. 05=> c = 18. 513 P(F 3, 6<c) = 0. 95 = 1 - P(F 3, 6>c) = 0. 05 => c = 4. 757
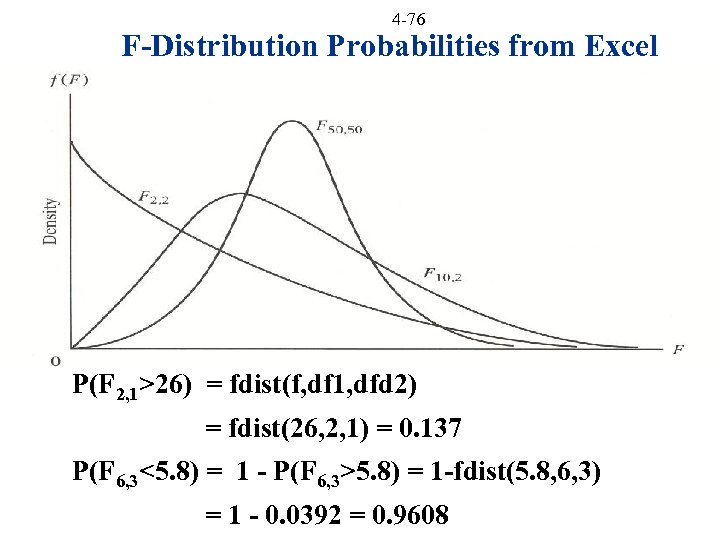
4 -76 F-Distribution Probabilities from Excel P(F 2, 1>26) = fdist(f, df 1, dfd 2) = fdist(26, 2, 1) = 0. 137 P(F 6, 3<5. 8) = 1 - P(F 6, 3>5. 8) = 1 -fdist(5. 8, 6, 3) = 1 - 0. 0392 = 0. 9608
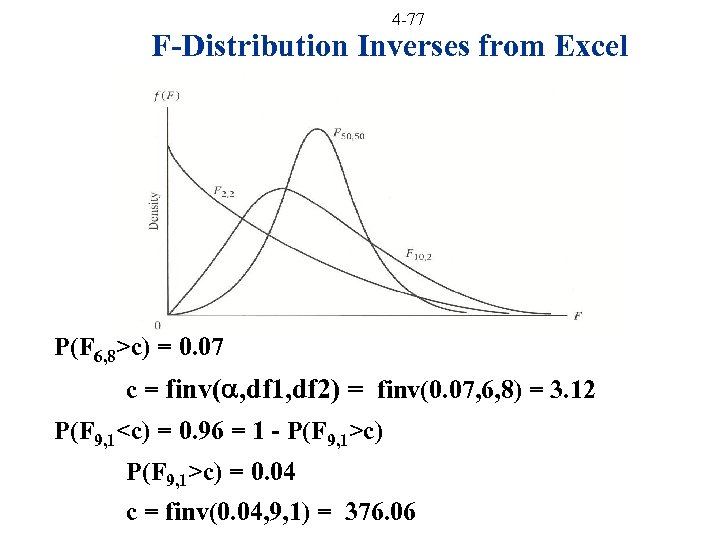
4 -77 F-Distribution Inverses from Excel P(F 6, 8>c) = 0. 07 c = finv( , df 1, df 2) = finv(0. 07, 6, 8) = 3. 12 P(F 9, 1<c) = 0. 96 = 1 - P(F 9, 1>c) = 0. 04 c = finv(0. 04, 9, 1) = 376. 06

4 -78 Cauchy Distribution a f(x) = π (x 2 + a 2) a>0, - <x< symmetric around 0 no moment generating but characteristic function like normal but fatter tails no variance can have bimodal t = 1 degree of freedom is a Cauchy

4 -79 Exponential f(x) = e-(x/ ) x>0 excel =expondist(x, , true) applications queuing theory continuous related to Poisson (same lambda) Poisson = number of repairs exponential time between repairs life of light bulbs

4 -80 Exponential graph the exponential function for = 1, 3, 10

4 -81 Exponential Example: When drilling oil well breakage or lost tool down hole fishing for it expensive no luck fishing deviate well Suppose fish time t ~ exponential =1/3. longer than 7 hours better to deviate percent of time better to deviate? =1 -expondist(7, 1/3, true)=0. 096972

4 -82 Integrate Exponential Functions Make review mineral examples to show to integrate ex, e-x, eax

4 -83 Integrate Exponential Functions Rules add example ¬ General integration rule: ∫ ekx dx = ekx / k for example ∫ ex dx = ex ¬ Integration by substitution rule: x 2 dx ∫ x e Substitute u = x 2 du = 2 x dx or dx = du/2 x Then ∫ x eu (du/2 x) = ½ ∫ eu du = ½ eu

4 -84 Integrate Exponential Functions Rules ¬ Integrate by parts ∫ x ex dx Let f (x) = x and g = ex, then f(x)= 1 and g(x) = ex x dx = f (x). g (x) - ∫ g (x). f (x) dx ∫ x e = x ex - ∫ ex dx = x ex – ex To check take the derivative for this expression (x ex - ex) it will give (x ex )

4 -85 Integrate Exponential Functions integrate by parts: v = x dv = dx u = e-λx du = -λe-λxdx

4 -86 Integrate Exponential Functions

4 -87 Integrate Exponential Functions If = 1 find P(x < 3)
4 -88 Log Normal X is lognormally distributed if Y = Ln(X) is normally distributed Uses - failure rates - mineral deposits

4 -89 Log Normal m = mean s = sigma = standard deviation Source: http: //mathworld. wolfram. com/Log. Normal. Distribution. html
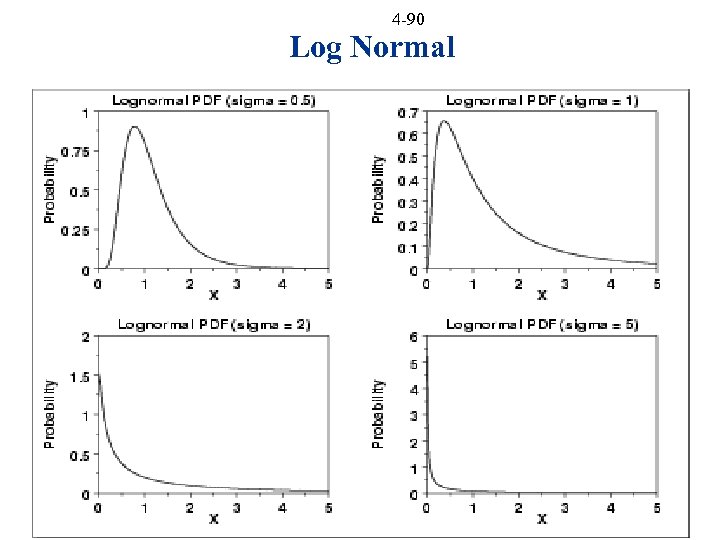
4 -90 Log Normal
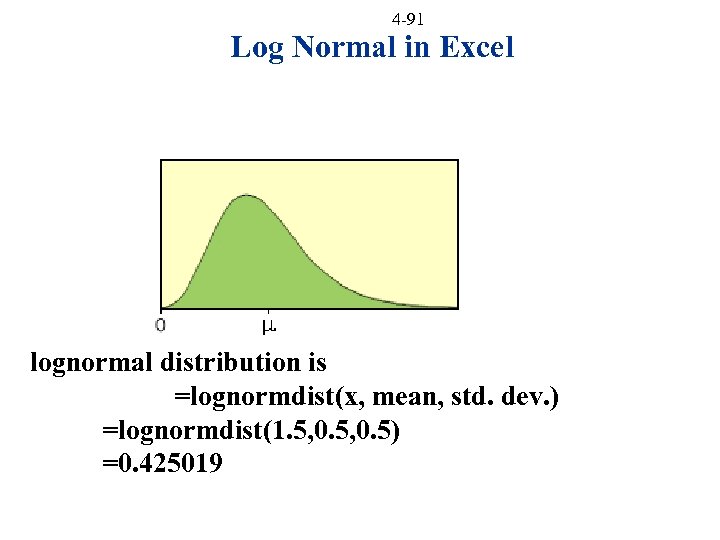
4 -91 Log Normal in Excel lognormal distribution is =lognormdist(x, mean, std. dev. ) =lognormdist(1. 5, 0. 5) =0. 425019

4 -92 Chapter 4 Sum Up Ø Special Distributions Powerful tools Ø Binomial Distribution Ø Normal Distribution Ø Poisson Distribution Ø Relations Between Distributions Binomial and Normal Binomial and Poisson and Normal

4 -93 Chapter 4 Sum Up Ø Central Limit Theorem Ø Multinomial Distribution Ø Hypergeometric Distribution Ø Uniform Distribution Ø Distributions from Normal 2 Distribution t-Distribution F-Distribution Y = ßo + ß 1 X 1 + ß 2 X 2 +

4 -94 Chapter 4 Sum Up Ø Cauchy Ø Exponential Ø Lognormal

4 -95 End of Chapter 4
d76252b226125ba7e6c42311c740493c.ppt