Special Inventory Models Supplement D 2007 Pearson

Special Inventory Models Supplement D © 2007 Pearson Education

Special Inventory Models Ø Three common situations require relaxation of one or more of the assumptions on which the EOQ model is based. Ø Noninstantaneous Replenishment occurs when production is not instantaneous and inventory is replenished gradually, rather than in lots. Ø Quantity Discounts occur when the unit cost of purchased materials is reduced for larger order quantities. Ø One-Period Decisions: Retailers and manufacturers of fashion goods often face situations in which demand is uncertain and occurs during just one period or season. © 2007 Pearson Education

Noninstantaneous Replenishment Ø If an item is being produced internally rather than purchased, finished units may be used or sold as soon as they are completed, without waiting until a full lot is completed. Ø Production rate, p, exceeds the demand rate, d. Ø Cycle inventory accumulates faster than demand occurs Ø a buildup of p – d units occurs per time period, continuing until the lot size, Q, has been produced. © 2007 Pearson Education

On-hand inventory Noninstantaneous Replenishment Production quantity Q Demand during production interval Imax Maximum inventory p–d Time Production and demand Demand only TBO © 2007 Pearson Education

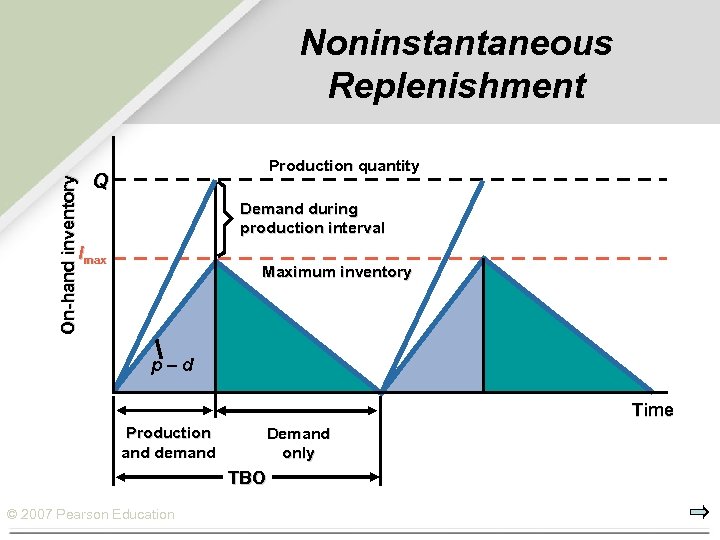
Noninstantaneous Replenishment Ø Cycle inventory is no longer Q/2, as it was with the basic EOQ method; instead, it is the maximum cycle inventory (Imax / 2) ( p–d Q Imax = (p – d) = Q p p ) Ø Total annual cost (C) = Annual holding cost + annual ordering or setup cost ( Q p–d C =2 p © 2007 Pearson Education ) D + (S) Q D = annual demand d = daily demand p = production rate S = setup costs Q = ELS

Economic Lot Size (ELS) Ø Economic production lot size (ELS) is the optimal lot size in a situation in which replenishment is not instantaneous. ELS = © 2007 Pearson Education 2 DS H p p–d D = annual demand d = daily demand p = production rate S = setup costs H = annual unit holding cost

Finding the ELS Example D. 1 1. 2. 3. 4. The manager of a chemical plant must determine the following for a particular chemical: Determine the economic production lot size (ELS). Determine the total annual setup and inventory holding costs. Determine the TBO, or cycle length, for the ELS. Determine the production time per lot. • What are the advantages of reducing the setup time by 10 percent? Demand = 30 barrels/day Production rate = 190 barrels/day Annual demand = 10, 500 barrels © 2007 Pearson Education Setup cost = $200 Annual holding cost = $0. 21/barrel Plant operates 350 days/year

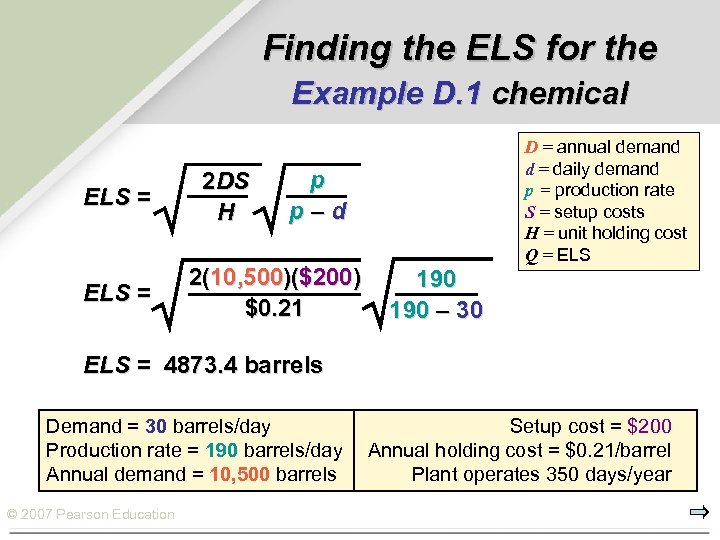Finding the ELS for the Example D. 1 chemical ELS = 2 DS H D = annual demand d = daily demand p = production rate S = setup costs H = unit holding cost Q = ELS p p–d 2(10, 500)($200) $0. 21 190 – 30 ELS = 4873. 4 barrels Demand = 30 barrels/day Production rate = 190 barrels/day Annual demand = 10, 500 barrels © 2007 Pearson Education Setup cost = $200 Annual holding cost = $0. 21/barrel Plant operates 350 days/year

Finding the Total Annual Cost Example D. 1 ( D = annual demand d = daily demand p = production rate S = setup costs H = unit holding cost Q = ELS ) Q p–d D C =2 (H ) + ( S) p Q ( ) 10, 500 4873. 4 190 – 30 C= ($0. 21) + ($200) 4873. 4 2 190 C = $430. 91 + $430. 91 Demand = 30 barrels/day Production rate = 190 barrels/day Annual demand = 10, 500 barrels © 2007 Pearson Education C = $861. 82 Setup cost = $200 Annual holding cost = $0. 21/barrel Plant operates 350 days/year

Finding the TBO Example D. 1 ELS TBOELS = (350 days/year) D 4873. 4 TBOELS = (350 days/year) 10, 500 D = annual demand d = daily demand p = production rate S = setup costs H = unit holding cost Q = ELS TBOELS = 162. 4, or 162 days Demand = 30 barrels/day Production rate = 190 barrels/day Annual demand = 10, 500 barrels © 2007 Pearson Education Setup cost = $200 Annual holding cost = $0. 21/barrel Plant operates 350 days/year

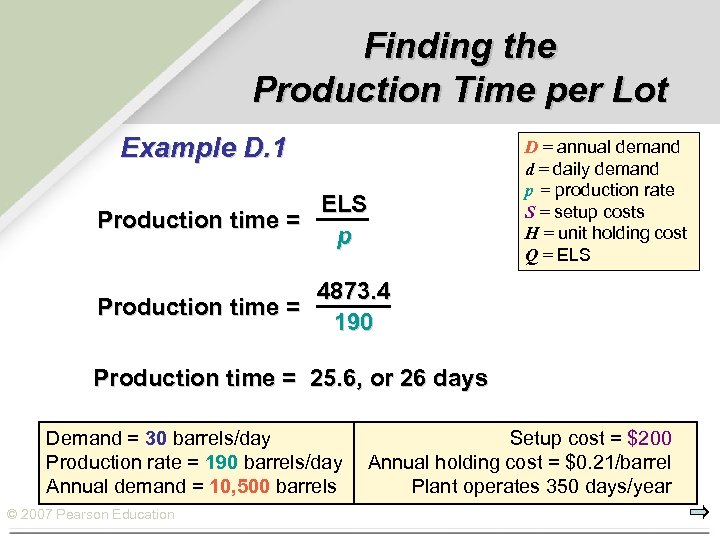Finding the Production Time per Lot Example D. 1 ELS Production time = p D = annual demand d = daily demand p = production rate S = setup costs H = unit holding cost Q = ELS 4873. 4 Production time = 190 Production time = 25. 6, or 26 days Demand = 30 barrels/day Production rate = 190 barrels/day Annual demand = 10, 500 barrels © 2007 Pearson Education Setup cost = $200 Annual holding cost = $0. 21/barrel Plant operates 350 days/year

Advantage of Reducing Setup Time OM Explorer Solver for the Economic Production Lot Size Showing the effect of a 10 Percent Reduction in setup cost. $180 vs original $200 © 2007 Pearson Education

Application D. 1 or 1555 engines © 2007 Pearson Education

Application D. 1 continued © 2007 Pearson Education

Quantity Discounts Ø Quantity discounts, which are price incentives to purchase large quantities, create pressure to maintain a large inventory. Ø For any per-unit price level, P, the total cost is: Total annual cost = Annual holding cost + Annual ordering or setup cost + Annual cost of materials D Q C= ( H) + (S) + PD Q 2 © 2007 Pearson Education D = annual demand S = setup costs P = per-unit price level H = unit holding cost Q = ELS

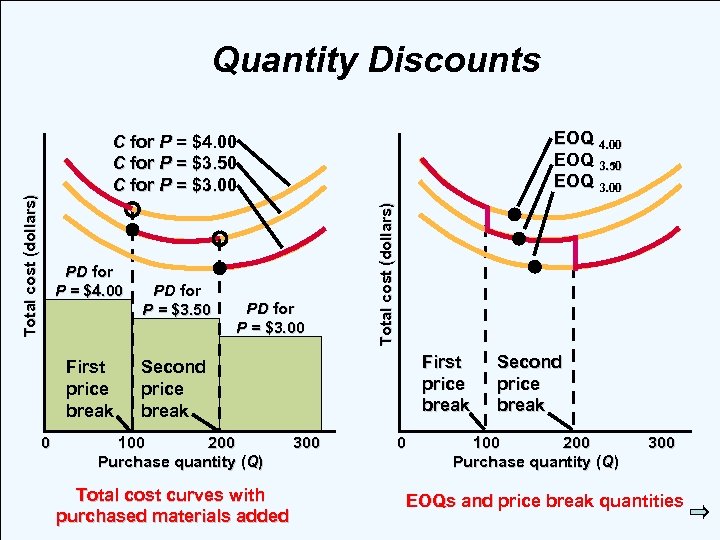Quantity Discounts EOQ 4. 00 EOQ 3. 50 EOQ 3. 00 PD for P = $4. 00 First price break 0 PD for P = $3. 50 PD for P = $3. 00 Total cost (dollars) C for P = $4. 00 C for P = $3. 50 C for P = $3. 00 First price break Second price break 100 200 Purchase quantity (Q) Total cost curves with © 2007 purchased materials added Pearson Education 300 0 Second price break 100 200 Purchase quantity (Q) 300 EOQs and price break quantities

Finding Q with Quantity Discounts Ø Step 1. Beginning with the lowest price, calculate the EOQ for each price level until a feasible EOQ is found. § It is feasible if it lies in the range corresponding to its price. Ø Step 2. If the first feasible EOQ found is for the lowest price level, this quantity is the best lot size. § Otherwise, calculate the total cost for the first feasible EOQ and for the larger price break quantity at each lower price level. The quantity with the lowest total cost is optimal. © 2007 Pearson Education

Example D. 2 A supplier for St. Le. Roy Hospital has introduced quantity discounts to encourage larger order quantities of a special catheter. The price schedule is: Order Quantity 0 – 299 300 – 499 500 or more Price per Unit $60. 00 $58. 80 $57. 00 Annual demand (D) = 936 units Ordering cost (S) = $45 Holding cost (H) = 25% of unit price Step 1: Start with lowest price level: EOQ 57. 00 = © 2007 Pearson Education 2 DS H = 2(936)(45) 0. 25(57. 00) = 77 units

Example D. 2 continued EOQ 57. 00 = 2 DS H = EOQ 58. 80 = 2 DS H EOQ 60. 00 = 2 DS H 2(936)(45) 0. 25(57. 00) = 77 units = 2(936)(45) 0. 25(58. 80) = 76 units = 2(936)(45) 0. 25(60. 00) = 75 units Not feasible Feasible This quantity is feasible because it lies in the range corresponding to its price. Order Quantity 0 – 299 300 – 499 500 or more © 2007 Pearson Education Price per Unit $60. 00 $58. 80 $57. 00 Annual demand (D) = 936 units Ordering cost (S) = $45 Holding cost (H) = 25% of unit price

Example D. 2 continued Ø Step 2: The first feasible EOQ of 75 does not correspond to C= Q 2 C 75 = the lowest price level. Hence, we must compare its total cost with the price break quantities (300 and 500 units) at the lower price levels ($58. 80 and $57. 00): D ( H) + ( S) + PD Q 936 75 [(0. 25)($60. 00)] + ($45) + $60. 00(936) C 75 = $57, 284 75 2 C 300 = 936 300 [(0. 25)($58. 80)] + ($45) + $58. 80(936) = $57, 382 300 2 936 500 C 500 = [(0. 25)($57. 00)] + ($45) + $57. 00(936) = $56, 999 500 2 The best purchase quantity is 500 units, which qualifies for the deepest discount. © 2007 Pearson Education

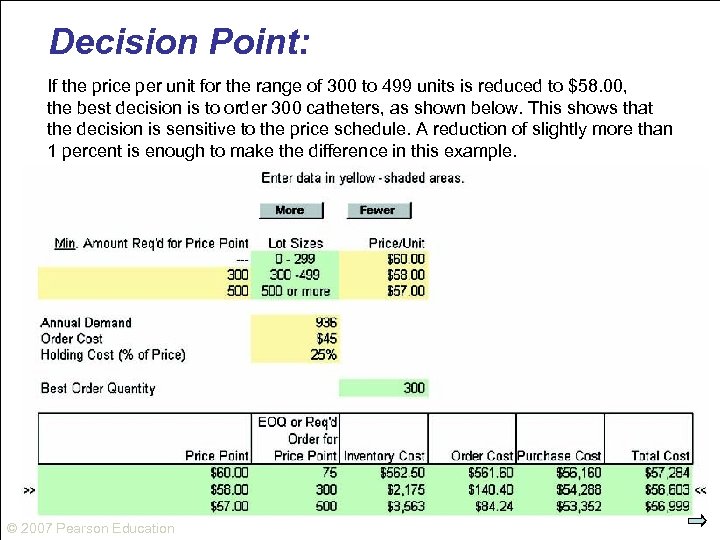Decision Point: If the price per unit for the range of 300 to 499 units is reduced to $58. 00, the best decision is to order 300 catheters, as shown below. This shows that the decision is sensitive to the price schedule. A reduction of slightly more than 1 percent is enough to make the difference in this example. © 2007 Pearson Education

Application D. 2 © 2007 Pearson Education

Application D. 2 Solution © 2007 Pearson Education

One-Period Decisions Ø This type of situation is often called the newsboy problem. If the newspaper seller does not buy enough newspapers to resell on the street corner, sales opportunities are lost. If the seller buys too many newspapers, the overage cannot be sold because nobody wants yesterday’s newspaper. 1. List the different levels of demand that are possible, along with the estimated probability of each. 2. Develop a payoff table that shows the profit for each purchase quantity, Q, at each assumed demand level. 3. Calculate the expected payoff for each Q (or row in the payoff table) by using the expected value decision rule. 4. Choose the order quantity Q with the highest expected payoff. © 2007 Pearson Education

One-Period Decisions Ø The payoff for a given quantity-demand combination depends on whether all units are sold at the regular profit margin, which results in two possible cases. 1. If demand is high enough (Q < D) then all of the cases are sold at the full profit margin, p, during the regular season. Payoff = (Profit per unit)(Purchase quantity) = p. Q 2. If the purchase quantity exceeds the eventual demand (Q > D), only D units are sold at the full profit margin, and the remaining units purchased must be disposed of at a loss, l, after the season. Payoff = (Profit per unit during season) (Demand) – (Loss per unit) (Amount disposed of after season) = p. D – l(Q – D) © 2007 Pearson Education

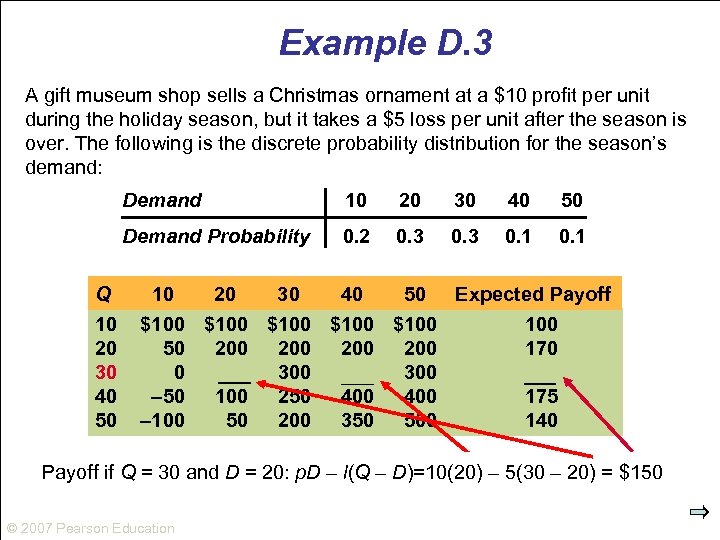Example D. 3 A gift museum shop sells a Christmas ornament at a $10 profit per unit during the holiday season, but it takes a $5 loss per unit after the season is over. The following is the discrete probability distribution for the season’s demand: Demand 20 30 40 50 Demand Probability Q 10 20 30 40 50 10 0. 2 0. 3 0. 1 10 20 30 40 50 Expected Payoff $100 $100 50 200 200 170 0 150 300 300 195 – 50 100 250 400 175 – 100 50 200 350 500 140 Payoff Expected payoff=ifand=D =D 0(0. 2)+(150(0. 3)+300(0. 3+0. 1) = = $150 Payoff if Qif=Q 30 and 20: 40: – l(Q – D)=10(20) – 5(30 – 20) $195 30 Q 30: = p. D = 10(30) = $300 © 2007 Pearson Education

Example D. 3 OM Explorer Solution © 2007 Pearson Education

Solved Problem 1 Ø For Peachy Keen, Inc. , the average demand for mohair sweaters is 100 per week. The production facility has the capacity to sew 400 sweaters per week. Setup cost is $351. The value of finished goods inventory is $40 per sweater. The annual perunit inventory holding cost is 20 percent of the item’s value. Ø a. What is the economic production lot size (ELS)? Ø b. What is the average time between orders (TBO)? Ø c. What is the minimum total of the annual holding cost and setup cost? © 2007 Pearson Education

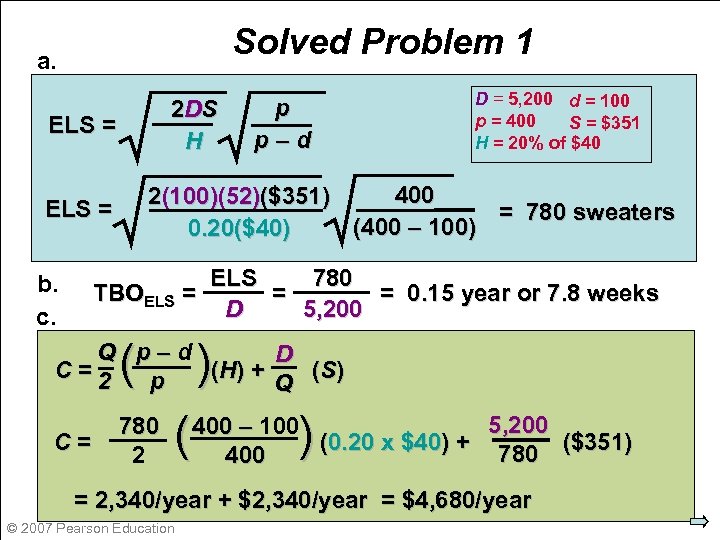Solved Problem 1 a. 2 DS H ELS = p p–d D = 5, 200 d = 100 p = 400 S = $351 H = 20% of $40 400 2(100)(52)($351) = 780 sweaters (400 – 100) 0. 20($40) ELS = ELS 780 = TBOELS = = 0. 15 year or 7. 8 weeks D 5, 200 b. c. ( ) Q p–d D C =2 (H ) + ( S) p Q C= 780 2 ( ) 5, 200 400 – 100 (0. 20 x $40) + 780 ($351) 400 = 2, 340/year + $2, 340/year = $4, 680/year © 2007 Pearson Education

Solved Problem 3 Ø For Swell Productions, a concession stand will sell poodle skirts and other souvenirs of the 1950 s a one-time event. Skirts are purchased for $40 each and are sold during for $75 each. Ø Unsold skirts can be returned for a refund of $30 each. Sales depend on the weather, attendance, and other variables. Ø The following table shows the probability of various sales quantities. How many skirts should be ordered? © 2007 Pearson Education

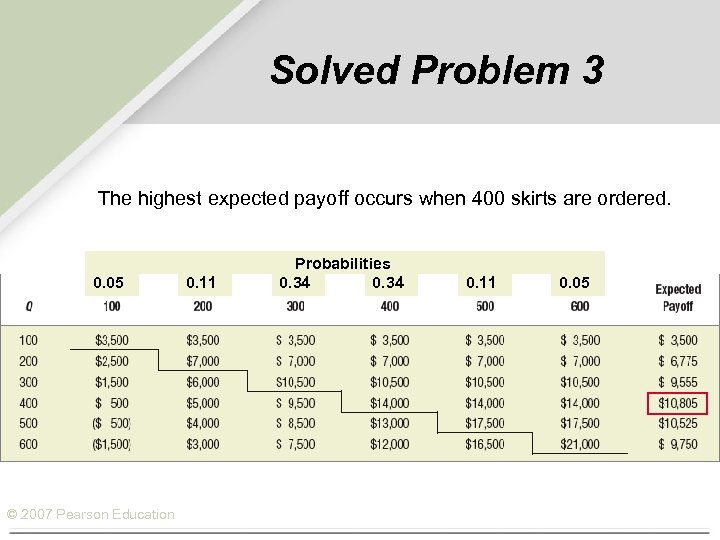Solved Problem 3 The highest expected payoff occurs when 400 skirts are ordered. 0. 05 © 2007 Pearson Education 0. 11 Probabilities 0. 34 0. 11 0. 05