СПб ГУТ им проф М А Бонч-Бруевича Инфокоммуникационные

СПб. ГУТ им. проф. М. А. Бонч-Бруевича Инфокоммуникационные системы 2014 г. 1

Непериодические колебания 2

Случайные колебания 3

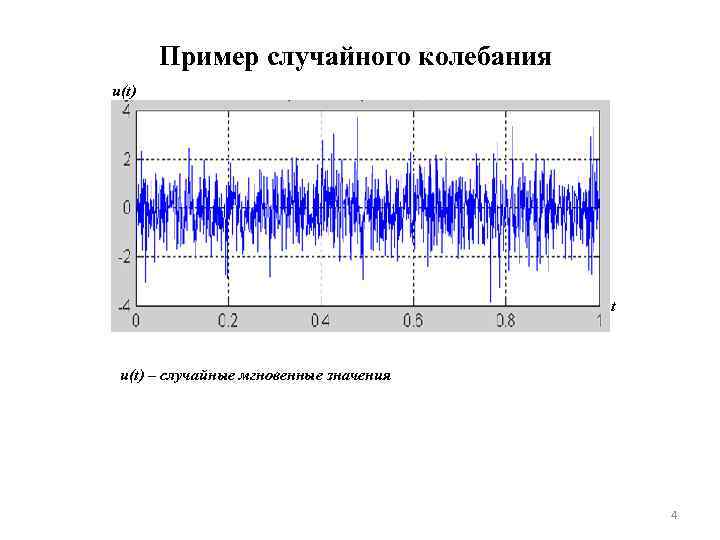
Пример случайного колебания u(t) t u(t) – случайные мгновенные значения 4

Параметры колебания u(t) Математическое ожидание 5

Параметры колебания u(t) Математическое ожидание Дисперсия 6

Параметры колебания u(t) Математическое ожидание Дисперсия Среднеквадратичное значение 7

Оценки параметров колебания u(t) 8

Оценки параметров колебания u(t) Оценка математического ожидания 9

Оценки параметров колебания u(t) Оценка математического ожидания Оценка дисперсии 10

Оценки параметров колебания u(t) Оценка математического ожидания Оценка дисперсии Оценка среднеквадратичного значение 11

Параметры колебания u(t) Плотность вероятности мгновенных значений - W(u) 12

Параметры колебания u(t) Плотность вероятности мгновенных значений - W(u) Нормальный закон распределения случайной величины u(t) 13

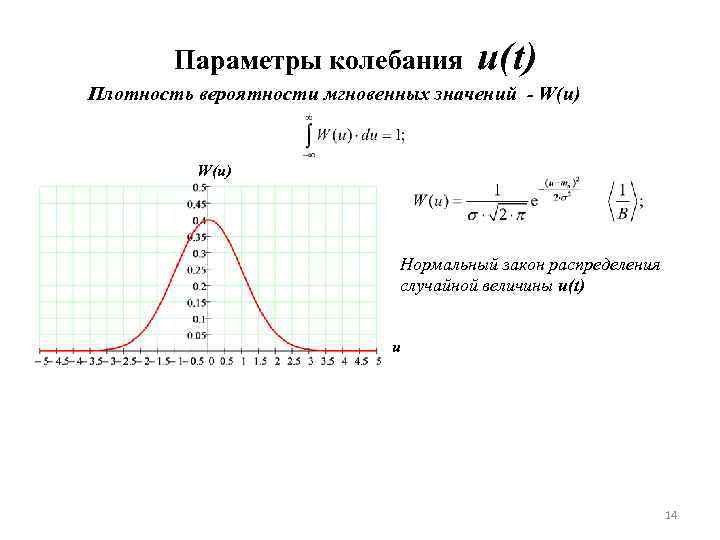
Параметры колебания u(t) Плотность вероятности мгновенных значений - W(u) Нормальный закон распределения случайной величины u(t) u 14

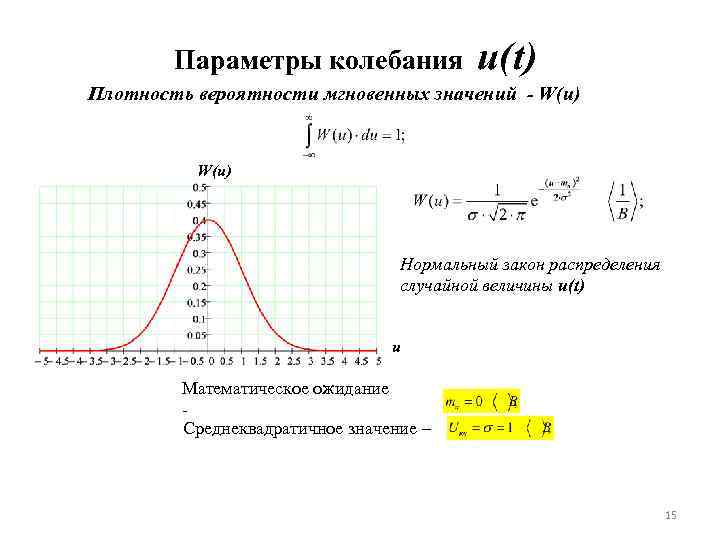
Параметры колебания u(t) Плотность вероятности мгновенных значений - W(u) Нормальный закон распределения случайной величины u(t) u Математическое ожидание Среднеквадратичное значение – 15

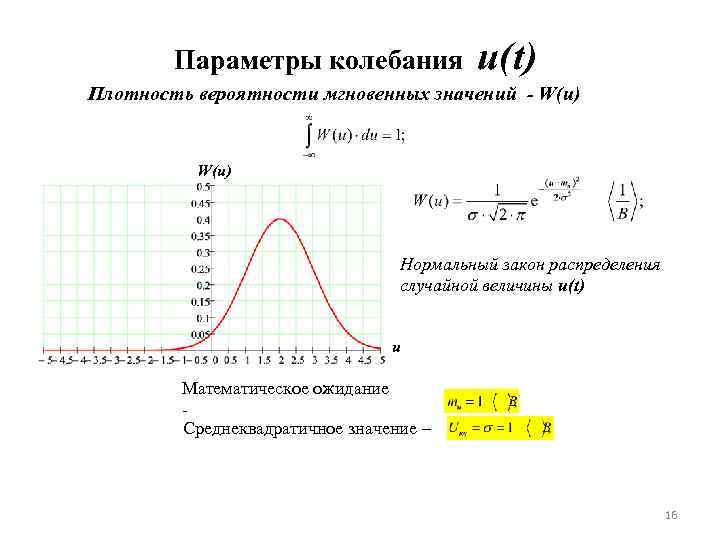
Параметры колебания u(t) Плотность вероятности мгновенных значений - W(u) Нормальный закон распределения случайной величины u(t) u Математическое ожидание Среднеквадратичное значение – 16

Параметры колебания u(t) Интегральная функция распределения - F(u) 17

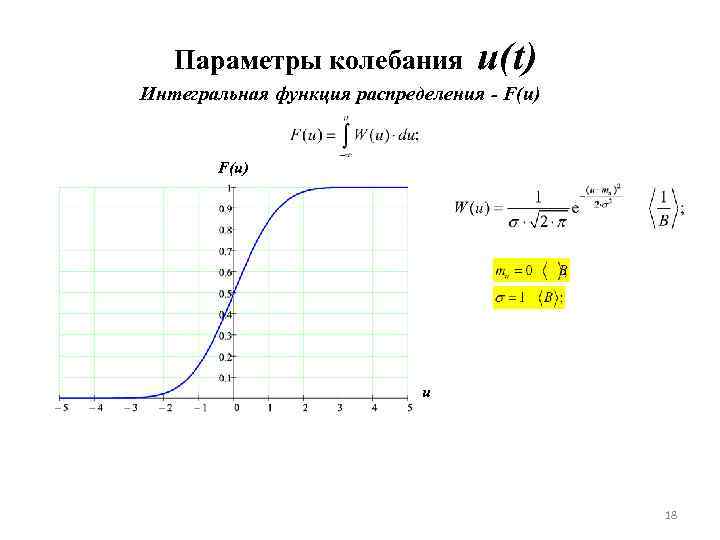
Параметры колебания u(t) Интегральная функция распределения - F(u) u 18

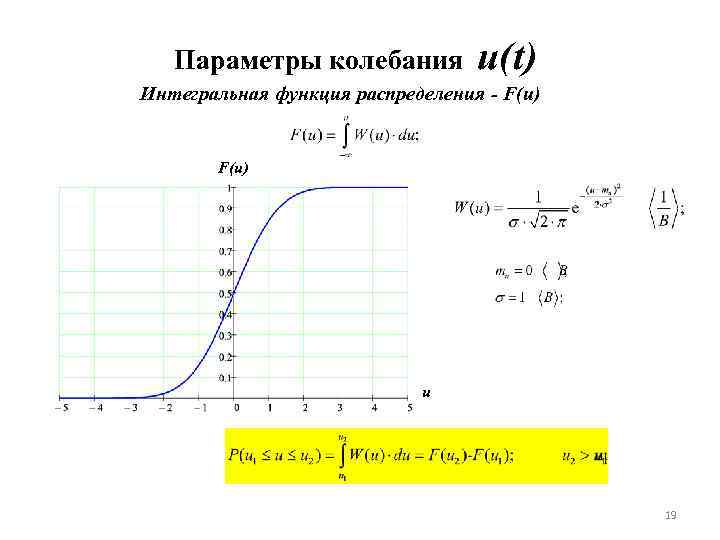
Параметры колебания u(t) Интегральная функция распределения - F(u) u 19

Параметры колебания u(t) Математическое ожидание 20

Параметры колебания u(t) Математическое ожидание Дисперсия 21

Параметры колебания u(t) Математическое ожидание Дисперсия Среднеквадратичное значение 22

Автокорреляционная функция колебания u(t) 23

Автокорреляционная функция колебания u(t) 24

Энергетический спектр колебания u(t) 25

Энергетический спектр колебания u(t) 26

Оценки характеристик колебания u(t) Автокорреляционная функция 27

Оценки характеристик колебания u(t) Автокорреляционная функция Энергетический спектр 28

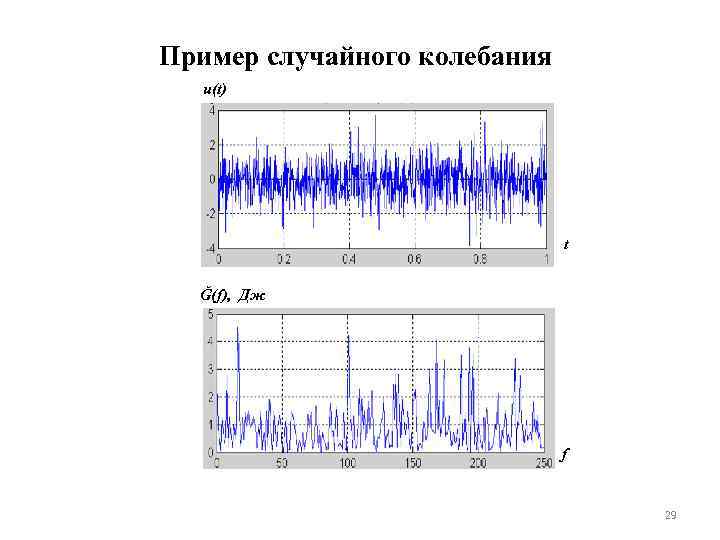
Пример случайного колебания u(t) t Ğ(f), Дж f 29

Тепловые шумы сопротивлений 1928 г. - обнаружение тепловых шумов Джонсоном. Теоретическое обоснование дано Найквистом. где: Uш – среднеквадратичное напряжение шума, В; k – постоянная Больцмана, 1, 38*10 -23 Дж/Ко; T – абсолютная температура, Ко; Re[Z(f)] – реальная составляющая сопротивления двухполюсника; f - частота. 30

Тепловые шумы сопротивлений 1928 г. - обнаружение тепловых шумов Джонсоном. Теоретическое обоснование дано Найквистом. где: Uш – среднеквадратичное напряжение шума, В; k – постоянная Больцмана, 1, 38*10 -23 Дж/Ко; T – абсолютная температура, Ко; Re[Z(f)] – реальная составляющая сопротивления двухполюсника; f - частота. Если Re[Z(f)]=R, 31

Тепловые шумы сопротивлений 1928 г. - обнаружение тепловых шумов Джонсоном. Теоретическое обоснование дано Найквистом. где: Uш – среднеквадратичное напряжение шума, В; k – постоянная Больцмана, 1, 38*10 -23 Дж/Ко; T – абсолютная температура, Ко; Re[Z(f)] – реальная составляющая сопротивления двухполюсника; f - частота. Если Re[Z(f)]=R, Энергетический спектр шума постоянен на всех частотах (Белый шум) При температуре 293 Ко Gш=1, 62 10 -20 Дж. В полосе частот Δf =1 МГц сопротивление R=10000 Ом создаёт шум мощностью Рш=1, 62*10 -10 Вт; шумовое напряжение Uш = 1, 27*10 -5 В 32

Токовые шумы где: Iш – среднеквадратичное значение шумового тока, А; e - заряд электрона, 1, 6*10 -19 К; I 0 - постоянная составляющая тока, А; Δf – полоса частот, Гц. 33

Токовые шумы где: Iш – среднеквадратичное значение шумового тока, А; e - заряд электрона, 1, 6*10 -19 К; I 0 - постоянная составляющая тока, А; Δf – полоса частот, Гц. Энергетический спектр шума постоянен на всех частотах (Белый шум) 34

Токовые шумы где: Iш – среднеквадратичное значение шумового тока, А; e - заряд электрона, 1, 62 10 -19 К; I 0 - постоянная составляющая тока, А; Δf – полоса частот, Гц. Энергетический спектр шума постоянен на всех частотах (Белый шум) При токе I 0 =1 м. А Gш=3, 2*10 -22 Дж, в полосе частот Δf = 1 МГц мощность шума равна Рш=3, 2*10 -16 Вт 35

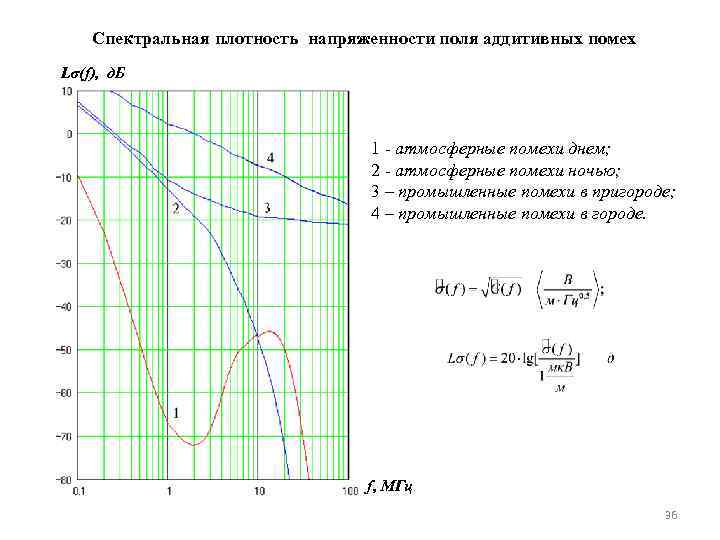
Спектральная плотность напряженности поля аддитивных помех Lσ(f), д. Б 1 - атмосферные помехи днем; 2 - атмосферные помехи ночью; 3 – промышленные помехи в пригороде; 4 – промышленные помехи в городе. f, МГц 36

Спасибо за внимание. 37