Spatiochromatic Vision Models for Imaging with Applications to

Spatiochromatic Vision Models for Imaging with Applications to the Development of Image Rendering Algorithms and Assessment of Image Quality Jan P. Allebach School of Electrical and Computer Engineering Purdue University West Lafayette, Indiana allebach@purdue. edu CIC-19, San Jose, CA, 8 November 2011

What is a model? From dictionary. com: A schematic description of a system, theory, or phenomenon that accounts for its known or inferred properties and may be used for further study of its characteristics. • Model is not a complete description of the phenomenon being modeled. • It should capture only what is important to the application at hand, and nothing more. • Its structure must be responsive to resource constraints. CIC-19, San Jose, CA, 8 November 2011 2/120

Visual system components CIC-19, San Jose, CA, 8 November 2011 3/120

Why do we need spatiochromatic models? • Imaging systems succeed by providing a facsimile of the real world • A few primaries instead of an exact spectral match • Spatially discretized and amplitude quantized representation of images that are continuous in both space and amplitude • These methods only succeed only because of the limitations of the human visual system (HVS) • To design lowest cost systems that achieve the desired objective, it is necessary to take into account the human visual system in the design and evaluation CIC-19, San Jose, CA, 8 November 2011 4/120

Modeling context • Modeling process is very dependent on the intended application - Motivation for developing the models in the first place - Governs choice of features to be captured and computational structure of the model - Provides the final test of the success of the model • Tight interplay between models for imaging system components and the human visual system • Model usage may be either embedded or external CIC-19, San Jose, CA, 8 November 2011 5/120

Pedagogical approach • Spatiochromatic modeling, in principle, builds on all of the following areas: - Color science - Imaging science - Psychophysics - Image systems engineering • As stated in course description, we assume only a rudimentary knowledge of these subjects • Start from basic principles, but move quickly to more advanced level • Focus on what is needed to follow the modeling discussion • See references at end CIC-19, San Jose, CA, 8 November 2011 6/120

Synopsis of tutorial • General framework for spatiochromatic models for the HVS • Introduction to digital halftoning • Application of spatiochromatic models to design of color halftones • Overview of use of HVS models in image quality assessment • Color Image Fidelity Assessor CIC-19, San Jose, CA, 8 November 2011 7/120

For further information • There is an extensive list of references at the end of these notes. • The powerpoint presentation may be downloaded from the web: https: //engineering. purdue. edu/~ece 638/ CIC-19, San Jose, CA, 8 November 2011 8/120

The retinal image is what counts • Every spatiochromatic model has an implied viewing distance • What happens when this condition is not met? - Too far – image looks better than specification - Too close – may see artifacts CIC-19, San Jose, CA, 8 November 2011 9/120

Basic spatiochromatic model structure CIC-19, San Jose, CA, 8 November 2011 10/120

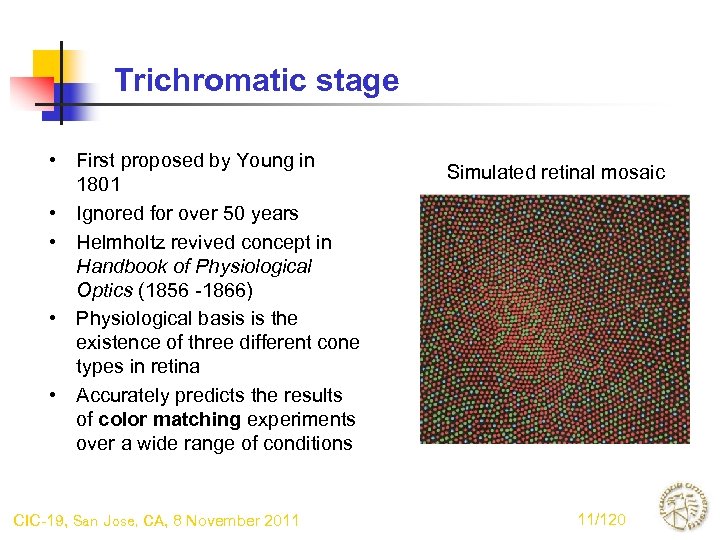Trichromatic stage • First proposed by Young in 1801 • Ignored for over 50 years • Helmholtz revived concept in Handbook of Physiological Optics (1856 -1866) • Physiological basis is the existence of three different cone types in retina • Accurately predicts the results of color matching experiments over a wide range of conditions CIC-19, San Jose, CA, 8 November 2011 Simulated retinal mosaic 11/120

Trichromatic sensor model • are spectral response functions that characterize the sensor • For the human visual system, the spectral response functions can be measured indirectly through color matching experiments CIC-19, San Jose, CA, 8 November 2011 12/120

Transformation between tristimulus representations • The trichromatic sensor model is applicable to a wide range of image capture devices, such as cameras and scanners, as well as the human visual system • If the spectral response functions are a linear transformation of those corresponding to the human visual system, then we call the 3 -tuple response the tristimulus coordinate of that spectral power distribution • For any two sets of spectral response functions that are both linear transformations of those for the human visual system, we can use a 3 x 3 matrix to transform between the corresponding tristimulus coordinates for any spectral stimulus • The color matching functions for visually independent primaries are also equivalent to the cone responses of the human visual system CIC-19, San Jose, CA, 8 November 2011 13/120

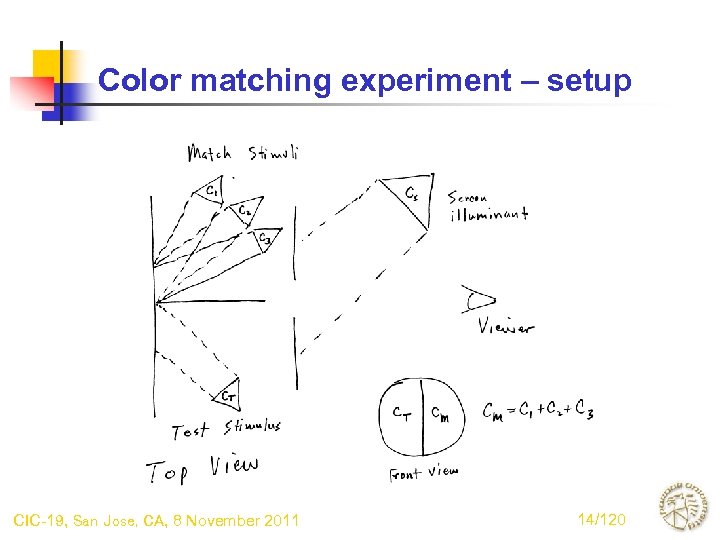Color matching experiment – setup CIC-19, San Jose, CA, 8 November 2011 14/120

Color matching experiment - procedure • Test stimulus is fixed • Observer individually adjusts strengths of the three match stimuli to achieve a visual match between the two sides of the split field • Mixture is assumed to be additive, i. e. radiant power of mixture in any wavelength interval is sum of radiant powers of the three match stimuli in the same interval • To achieve a match with some test stimuli , it may be necessary to move one or two of the match stimuli over to the side where the test stimulus is located • For visually independent primaries, match amounts are equivalent to tristimulus coordinates CIC-19, San Jose, CA, 8 November 2011 15/120

Color matching functions • A color matching experiment yields the amount of each of three primaries required to match a particular stimulus • A special case is a monochromatic stimulus with wavelength • If we repeat this experiment for all wavelengths , we obtain color matching functions • Since any stimulus can be expressed as a weighted sum of monochromatic stimuli, the primary match amounts can be expressed as CIC-19, San Jose, CA, 8 November 2011 16/120

CIE 1931 standard RGB observer • Observer consists of color matching functions corresponding to monochromatic primaries • Primaries - R – 700 nm - G – 546. 1 nm - B – 435. 8 nm • Ratio of radiances • Chosen to place chromaticity of equal energy stimulus E at center of (r-g) chromaticity diagram, i. e. at (0. 333, 0. 333) that areas under color matching functions are identical. • Based on observations in a 2 degree field of view using color matching method discussed earlier. CIC-19, San Jose, CA, 8 November 2011 17/120

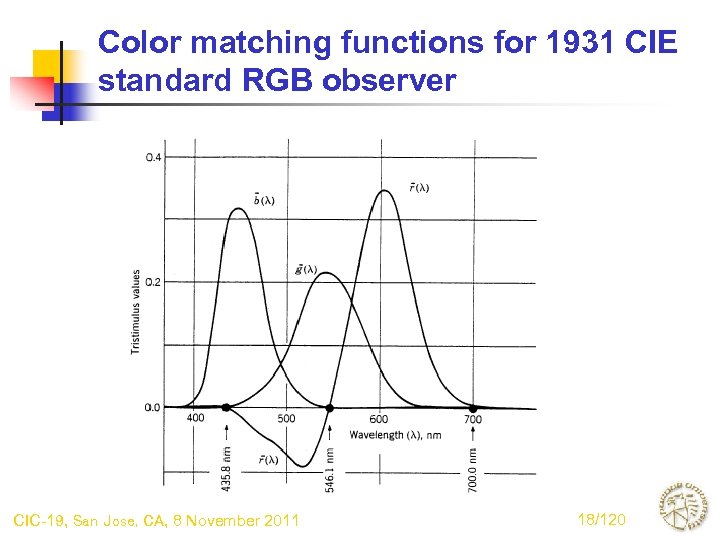Color matching functions for 1931 CIE standard RGB observer CIC-19, San Jose, CA, 8 November 2011 18/120

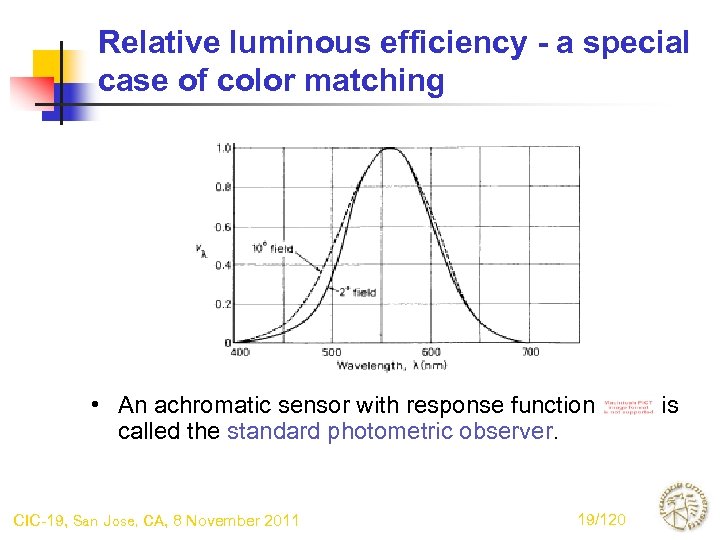Relative luminous efficiency - a special case of color matching • An achromatic sensor with response function called the standard photometric observer. CIC-19, San Jose, CA, 8 November 2011 19/120 is

CIE 1931 standard XYZ observer • The CIE also defined a second standard observer based on a linear transformation from the 1931 RGB color matching functions. • The XYZ observer has the following properties: - The color matching functions are nonnegative at all wavelengths. The chromaticity coordinates of all realizable stimuli are non-negative. - The color matching function is equal to the relative luminous efficiency function • To achieve these properties, it was necessary to use primaries that are not realizable. • The chromaticities of the primaries lie outside the spectral locus. CIC-19, San Jose, CA, 8 November 2011 20/120

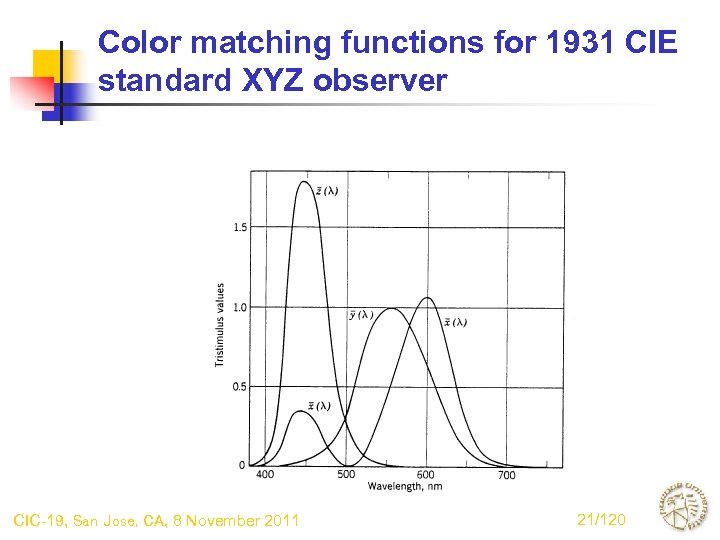Color matching functions for 1931 CIE standard XYZ observer CIC-19, San Jose, CA, 8 November 2011 21/120

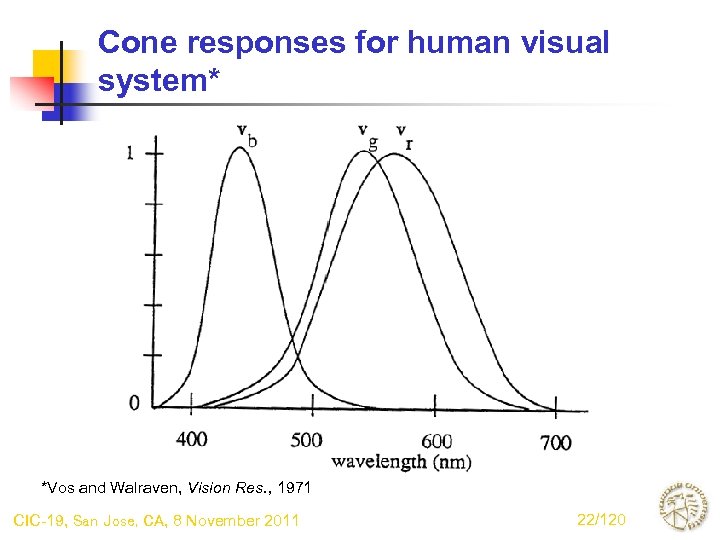Cone responses for human visual system* *Vos and Walraven, Vision Res. , 1971 CIC-19, San Jose, CA, 8 November 2011 22/120

Chromaticity coordinates • Chromaticity coordinates provide an important method for visualizing tristimulus coordinates, i. e. sensor responses or primary match amounts • Let denote either the sensor response or the primary match amounts for a particular stimulus • The corresponding chromaticity coordinates are defined as • We can see by inspection that each coordinate lies between 0 and 1 and that all three coordinates sum to 1 CIC-19, San Jose, CA, 8 November 2011 23/120

Chromaticity diagram for 1931 CIE standard XYZ observer CIC-19, San Jose, CA, 8 November 2011 24/120

How do we use the trichromatic model? • Assuming image is in a standard color space, such as s. RGB, we transform to CIE XYZ as follows: • Remove gamma correction, and transform to linear RGB • Perform 3 x 3 matrix transform from linear RGB to CIE XYZ • The CIE XYZ representation of the image will form the basis for further stages of the model CIC-19, San Jose, CA, 8 November 2011 25/120

Basic spatiochromatic model structure CIC-19, San Jose, CA, 8 November 2011 26/120

Opponent stage • Trichromatic theory provides the basis for understanding whether or not two spectral power distributions will appear the same to an observer when viewed under the same conditions. • However, the trichromatic theory will tell us nothing about the appearance of a stimulus. • In the early 1900’s, Ewald Hering observed some properties of color appearance - Red and green never occur together – there is no such thing as a reddish green, or a greenish red - If I add a small amount of blue to green, it looks bluish-green. If I add more blue to green, it becomes cyan. - In contrast, if I add red to green, the green becomes less saturated. If I add enough red to green, the color appears gray, blue, or yellow - If I add enough red to green, the color appears red, but never reddish green CIC-19, San Jose, CA, 8 November 2011 27/120

Blue-yellow color opponency CIC-19, San Jose, CA, 8 November 2011 28/120

Opponent stage (cont. ) • Hering postulated that there existed two kinds of neural pathways in the visual system - Red-Green pathway fires fast if there is a lot of red, fires slowly if there is a lot of green - Blue-Yellow pathway fires fast if there is a lot of blue, fires slowly if there is a lot of yellow • Hering provided no experimental evidence for his theory; and it was ignored for over 50 years CIC-19, San Jose, CA, 8 November 2011 29/120

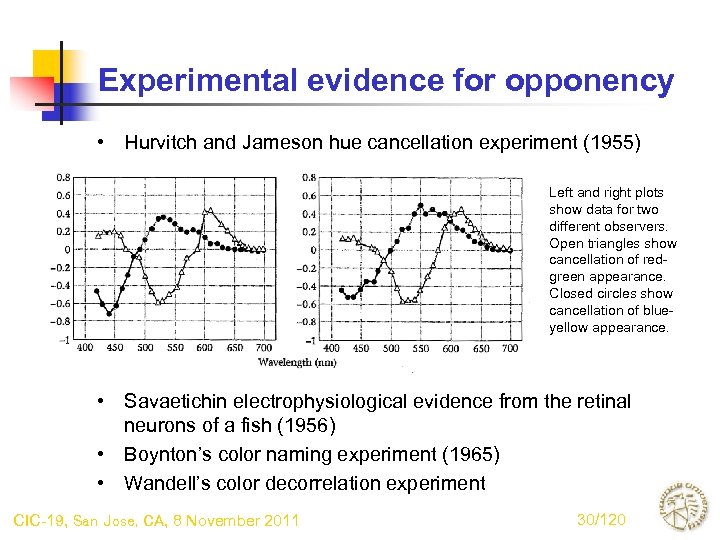Experimental evidence for opponency • Hurvitch and Jameson hue cancellation experiment (1955) • Left and right plots show data for two different observers. Open triangles show cancellation of redgreen appearance. Closed circles show cancellation of blueyellow appearance. • Savaetichin electrophysiological evidence from the retinal neurons of a fish (1956) • Boynton’s color naming experiment (1965) • Wandell’s color decorrelation experiment CIC-19, San Jose, CA, 8 November 2011 30/120

Color spaces that incorporate opponency • • • YUV (NTSC video standard space) YCr. Cb (Kodak Photo. CD space) L*a*b* (CIE uniform color space) YCx. Cz (Linearized CIE L*a*b* space) O 1 O 2 O 3 (Wandell’s optimally decorrelated space) CIC-19, San Jose, CA, 8 November 2011 31/120

CIE L*a*b* and its linearized version YCx. Cz in terms of CIE XYZ • CIE L*a*b* { L* = 116 f(Y/Yn) - 16 f(x) = 7. 787 x +16/116 0 x 0. 008856 x 1/3 0. 008856 x 1 a* = 200[f(X/Xn) - f(Y/Yn) ] b* = 500[f(Y/Yn) - f(Z/Zn) ] white point : (Xn, Yn, Zn) L* -a* -b* +b* • Linearized opponent color space Yy. Cx. Cz +a* Yy = 116 (Y/Yn) correlate of luminance Cx = 200[(X/Xn) - (Y/Yn) ] R-G opponent color chrominance channel Cz = 500[(Y/Yn) - (Z/Zn) ] Y-B opponent color chrominance channel CIC-19, San Jose, CA, 8 November 2011 32/120

Wandell’s space in terms of CIE XYZ* *Wen Wu, “Two Problems in Digital Color Imaging: Colorimetry and Image Fidelity Assessor, ” Ph. D. Dissertation, Purdue University, Dec. 2000 CIC-19, San Jose, CA, 8 November 2011 33/120

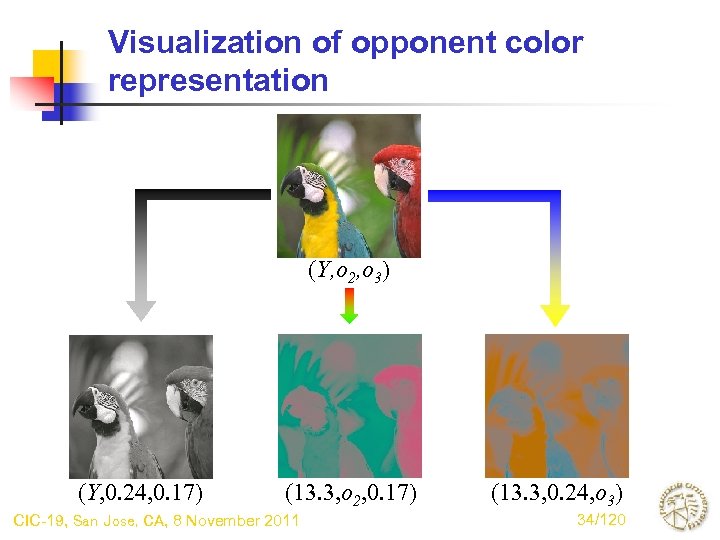Visualization of opponent color representation (Y, o 2, o 3) (Y, 0. 24, 0. 17) (13. 3, o 2, 0. 17) CIC-19, San Jose, CA, 8 November 2011 (13. 3, 0. 24, o 3) 34/120

Basic spatiochromatic model structure CIC-19, San Jose, CA, 8 November 2011 35/120

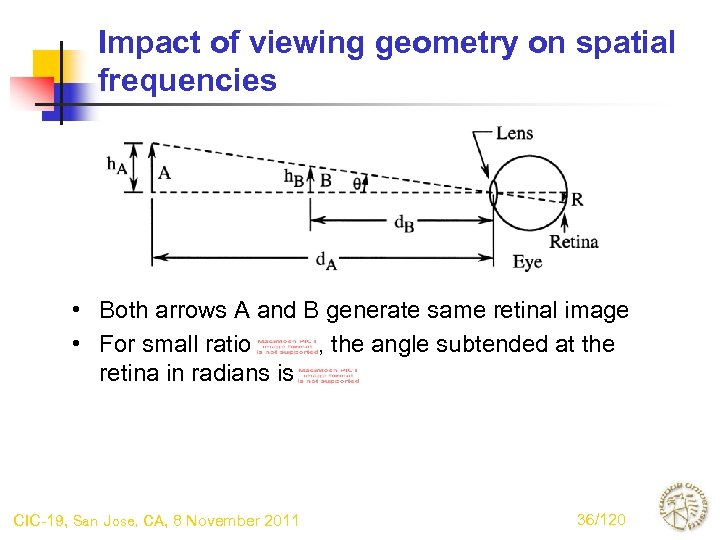Impact of viewing geometry on spatial frequencies • Both arrows A and B generate same retinal image • For small ratio , the angle subtended at the retina in radians is CIC-19, San Jose, CA, 8 November 2011 36/120

Spatial frequency conversion • To convert between (cycles/inch) viewed at distance (inches) and (cycles/degree) subtended at the retina, we thus have • For a viewing distance of 12 inches, this becomes CIC-19, San Jose, CA, 8 November 2011 37/120

Spatial frequency filtering stage • Based on pyschophysical measurements of contrast sensitivity function • Use sinusoidal stimuli with modulation along achromatic, red-green, or blue-yellow axes • For any fixed spatial frequency, threshold of visibility is depends only on. This is Weber’s Law. CIC-19, San Jose, CA, 8 November 2011 38/120

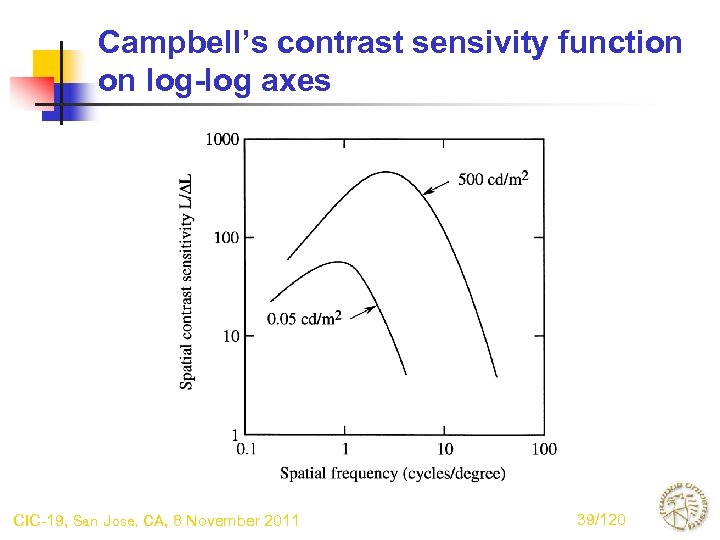Campbell’s contrast sensivity function on log-log axes CIC-19, San Jose, CA, 8 November 2011 39/120

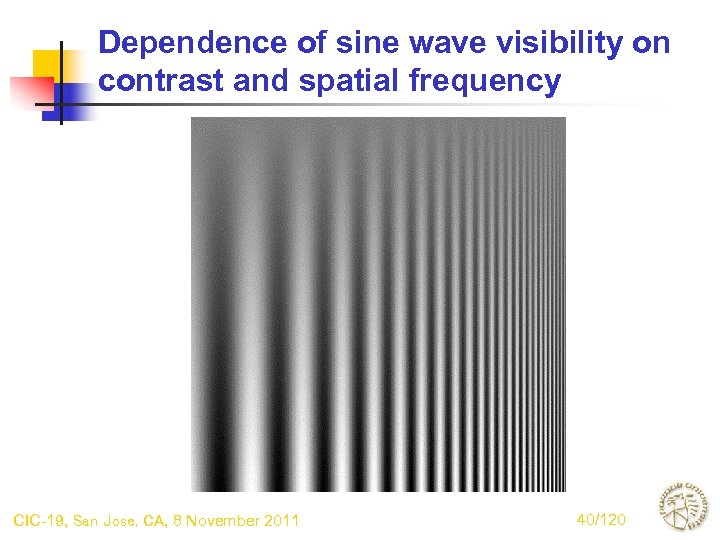Dependence of sine wave visibility on contrast and spatial frequency CIC-19, San Jose, CA, 8 November 2011 40/120

Models for achromatic spatial contrast sensitivty* *Kim and Allebach, IEEE T-IP, March 2002 Author Contrast sensitivity function Constants Campbell 1969 Mannos 1974 Nasanen 1984 Daly 1987 CIC-19, San Jose, CA, 8 November 2011 41/120

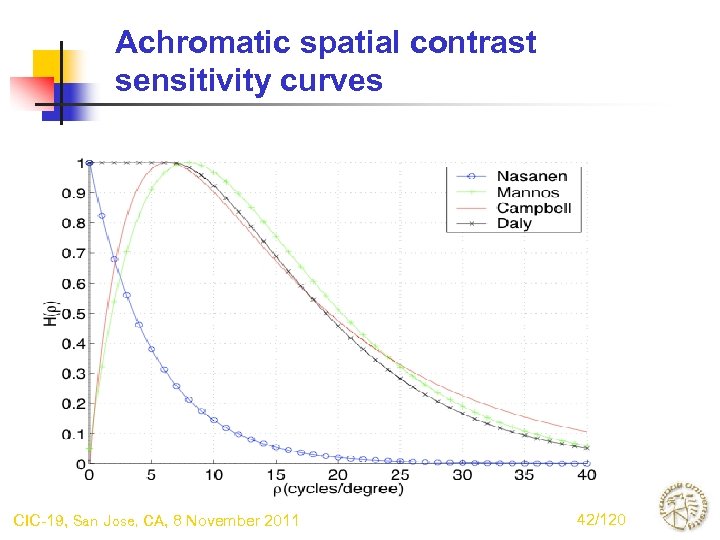Achromatic spatial contrast sensitivity curves CIC-19, San Jose, CA, 8 November 2011 42/120

Chrominance spatial frequency response • Based on Mullen’s data* *K. T. Mullen, J. Physiol. , 1985 CIC-19, San Jose, CA, 8 November 2011 43/120

Spatial Frequency Response of Opponent Channels Luminance [Nasanen] Chrominance [Kolpatzik and Bouman*] *B. Kolpatzik, and C. A. Bouman, J. Electr. Imaging, July 1992 CIC-19, San Jose, CA, 8 November 2011 44/120

Illustration of difference in spatial frequency response of luminance and chrominance channels Original image CIC-19, San Jose, CA, 8 November 2011 O 1 - filtered 45/120

Illustration of difference in spatial frequency response of luminance and chrominance channels Original image CIC-19, San Jose, CA, 8 November 2011 O 2 - filtered 46/120

Illustration of difference in spatial frequency response of luminance and chrominance channels Original image CIC-19, San Jose, CA, 8 November 2011 O 3 - filtered 47/120

Application areas for spatiochromatic models • Color image display on low-cost devices - PDA - Cellphone • Color image printing - Inkjet - Laser electrophotographic • Digital video display - LCD - DMD - Plasma panel • Lossy color image compression - JPEG - MPEG CIC-19, San Jose, CA, 8 November 2011 48/120

Synopsis of tutorial • General framework for spatiochromatic models for the HVS • Introduction to digital halftoning • Application of spatiochromatic models to design of color halftones • Overview of use of HVS models in image quality assessment • Color Image Fidelity Assessor CIC-19, San Jose, CA, 8 November 2011 49/120

What is digital halftoning? • Digital halftoning is the process of rendering a continuous-tone image with a device that is capable of generating only two or a few levels of gray at each point on the device output surface. • The perception of additional levels of gray depends on a local average of the binary or multilevel texture. CIC-19, San Jose, CA, 8 November 2011 50/120

What is digital halftoning (cont. ) • Detail is rendered by local modulation of the texture CIC-19, San Jose, CA, 8 November 2011 51/120

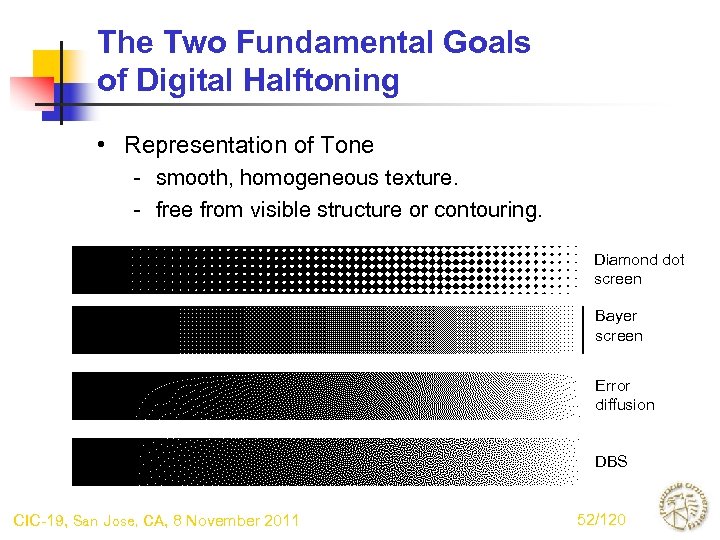The Two Fundamental Goals of Digital Halftoning • Representation of Tone - smooth, homogeneous texture. - free from visible structure or contouring. Diamond dot screen Bayer screen Error diffusion DBS CIC-19, San Jose, CA, 8 November 2011 52/120

The Two Fundamental Goals of Digital Halftoning (cont. ) • Representation of Detail - sharp, distinct, and good contrast in rendering of fine structure in image. - good rendering of lines, edges, and type characters. - freedom from moire due to interference between halftone algorithm and image content Diamond dot DBS screen CIC-19, San Jose, CA, 8 November 2011 Error diffusion DBS 53/120

Types of Halftone Texture Periodic Aperiodic Clustered Dot Dispersed Dot CIC-19, San Jose, CA, 8 November 2011 54/120

Basic structure of screening algorithm The threshold matrix is periodically tiled over the entire continuous-tone image. CIC-19, San Jose, CA, 8 November 2011 55/120

Error diffusion f[m, n] + - u[m, n] Q( • ) wk, l CIC-19, San Jose, CA, 8 November 2011 g[m, n] + d[m, n] 56/120

Direct binary search* Printer model *D. Lieberman and J. P. Allebach, IEEE T-IP, Nov. 2002 CIC-19, San Jose, CA, 8 November 2011 57/120

The Search Heuristic CIC-19, San Jose, CA, 8 November 2011 58/120

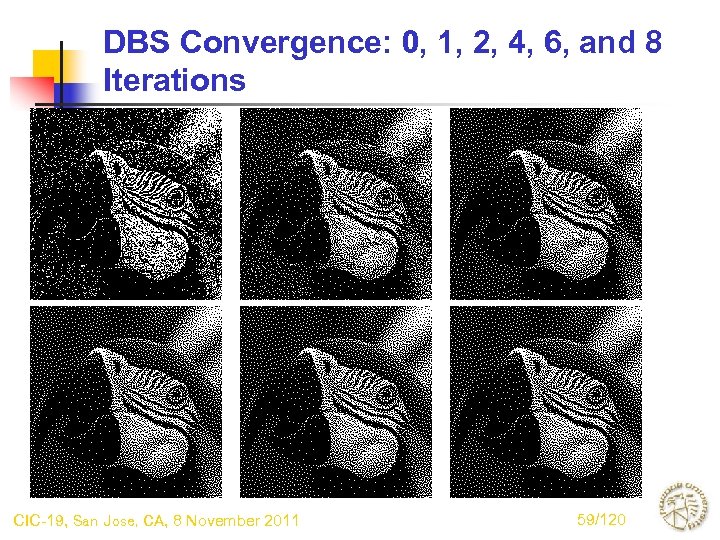DBS Convergence: 0, 1, 2, 4, 6, and 8 Iterations CIC-19, San Jose, CA, 8 November 2011 59/120

Swaps vs. Toggles Toggle only CIC-19, San Jose, CA, 8 November 2011 Swap and toggle 60/120

Dual interpretation for DBS • Minimize mean-squared error at distance D • Minimize maximum error at distance 2 D CIC-19, San Jose, CA, 8 November 2011 61/120

Illustration of Dual Interpretation f[m] g[m] CIC-19, San Jose, CA, 8 November 2011 ~ f[m]*p[m] ~ g[m]*p[m] f[m]*c~~[m] pp g[m]*c~~ [m] pp 62/120

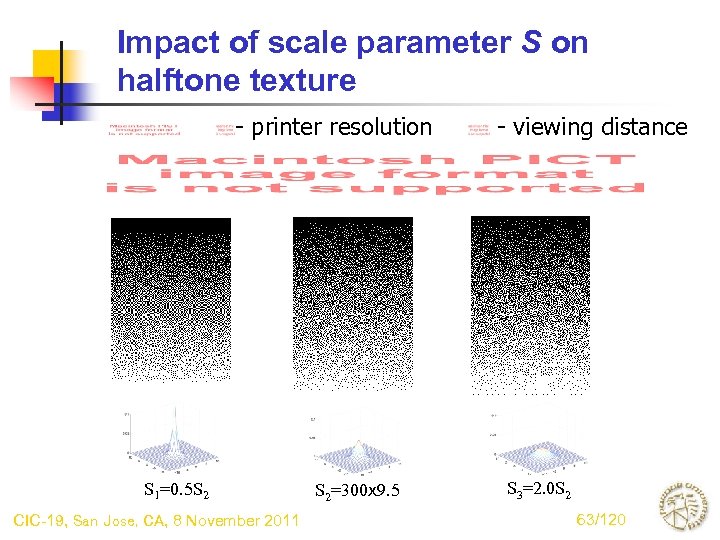Impact of scale parameter S on halftone texture - printer resolution S 1=0. 5 S 2 CIC-19, San Jose, CA, 8 November 2011 S 2=300 x 9. 5 - viewing distance S 3=2. 0 S 2 63/120

Does it make a difference which model we use? • Reason for normalization - Bandwidths of models differ significantly. - Causes a significant difference in texture between the models. - For any fixed model, can achieve a similar range of textures by varying scale parameter. - Would like to compare the models at the same texture scale. • Normalization method - Match the 50% point from the maximum for Nasanen’s model. CIC-19, San Jose, CA, 8 November 2011 64/120

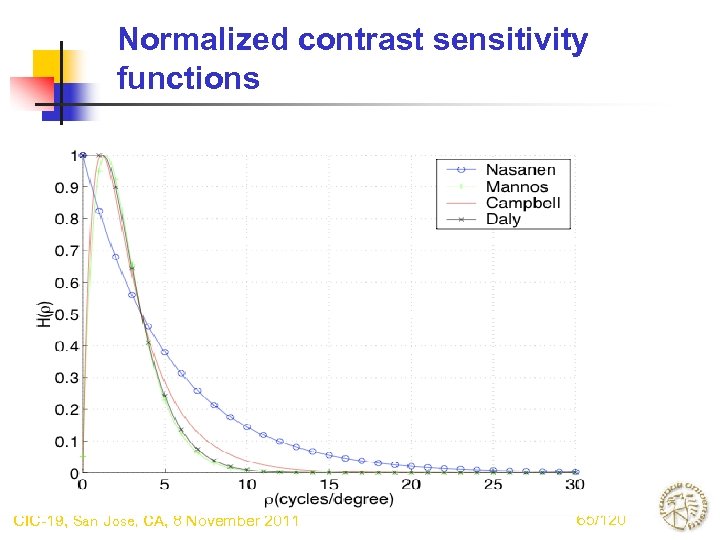Normalized contrast sensitivity functions CIC-19, San Jose, CA, 8 November 2011 65/120

Comparison between models Nasanen Campbell CIC-19, San Jose, CA, 8 November 2011 Daly Mannos 66/120

Comparison between models (cont. ) • In 2003, Monga, Geisler, and Evans published a comparision of the effectiveness of four different color HVS models in the context of error diffusion halftoning* • They concluded that the Flohr et al** model resulted in the best overall image quality *V. Monga, W. Geisler, B. L. Evans, IEEE SP Letters, April 2003 **U. Agar and J. P. Allebach, IEEE T-IP, Dec. 2005 CIC-19, San Jose, CA, 8 November 2011 67/120

Synopsis of tutorial • General framework for spatiochromatic models for the HVS • Introduction to digital halftoning • Application of spatiochromatic models to design of color halftones - Embedding of spatiochromatic model within DBS for color halftoning - Use of spatiochromatic model with hybrid screen to improve highlight texture - Application of spatiochromatic model to design of tile sets for periodic clustered-dot screens • Overview of use of HVS models in image quality assessment • Color Image Fidelity Assessor CIC-19, San Jose, CA, 8 November 2011 68/120

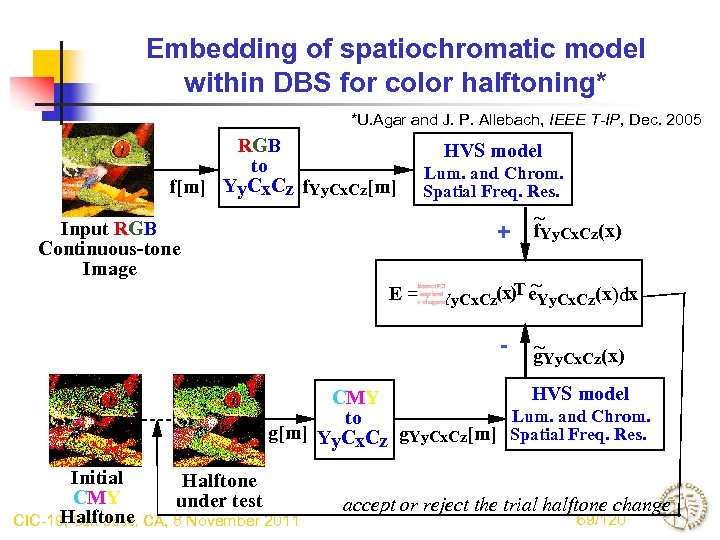Embedding of spatiochromatic model within DBS for color halftoning* *U. Agar and J. P. Allebach, IEEE T-IP, Dec. 2005 RGB to f[m] Yy. Cx. Cz f. Yy. Cx. Cz[m] Input RGB Continuous-tone Image HVS model Lum. and Chrom. Spatial Freq. Res. + ~ f. Yy. Cx. Cz(x) ~ ~ E = e. Yy. Cx. Cz(x)T e. Yy. Cx. Cz(x)dx - ~ g. Yy. Cx. Cz(x) HVS model CMY Lum. and Chrom. to g[m] Yy. Cx. Cz g. Yy. Cx. Cz[m] Spatial Freq. Res. Initial Halftone CMY under test Halftone CIC-19, San Jose, CA, 8 November 2011 accept or reject the trial halftone change 69/120

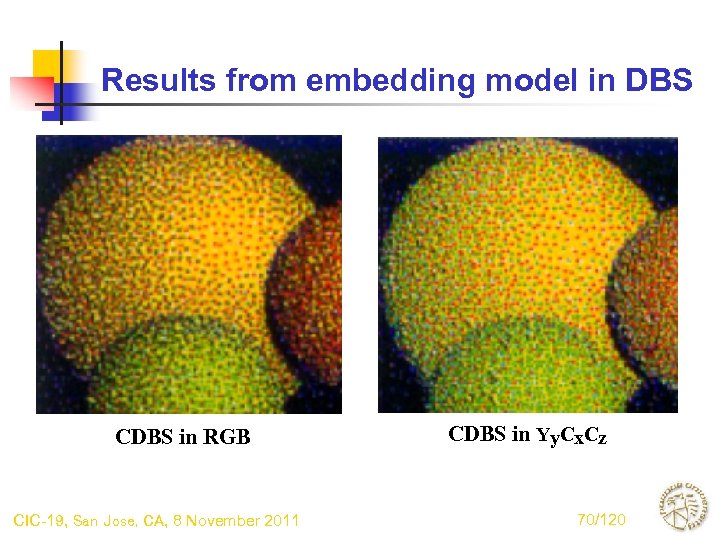Results from embedding model in DBS CDBS in RGB CIC-19, San Jose, CA, 8 November 2011 CDBS in Yy. Cx. Cz 70/120

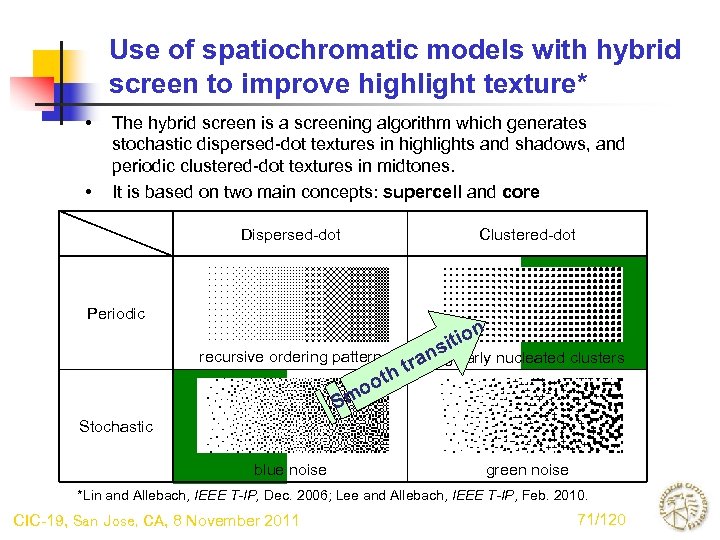Use of spatiochromatic models with hybrid screen to improve highlight texture* • • The hybrid screen is a screening algorithm which generates stochastic dispersed-dot textures in highlights and shadows, and periodic clustered-dot textures in midtones. It is based on two main concepts: supercell and core Dispersed-dot Clustered-dot Periodic recursive ordering pattern n tio i ns regularly nucleated clusters ra t th oo m S Stochastic blue noise green noise *Lin and Allebach, IEEE T-IP, Dec. 2006; Lee and Allebach, IEEE T-IP, Feb. 2010. CIC-19, San Jose, CA, 8 November 2011 71/120

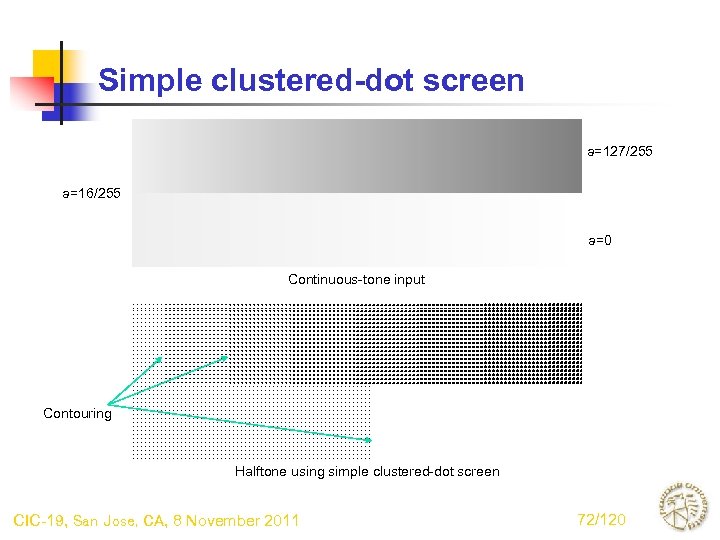Simple clustered-dot screen a=127/255 a=16/255 a=0 Continuous-tone input Contouring Halftone using simple clustered-dot screen CIC-19, San Jose, CA, 8 November 2011 72/120

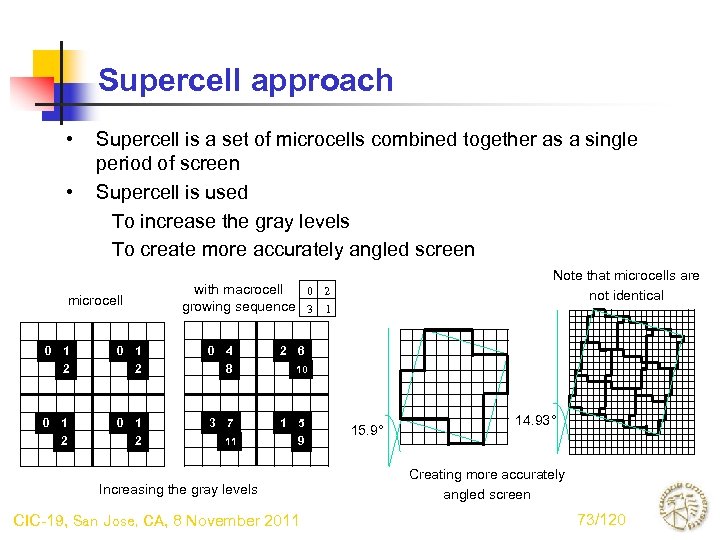Supercell approach • • Supercell is a set of microcells combined together as a single period of screen Supercell is used To increase the gray levels To create more accurately angled screen microcell Note that microcells are not identical with macrocell 0 2 growing sequence 3 1 0 1 2 0 4 8 2 6 0 1 2 3 7 1 5 9 11 10 Increasing the gray levels CIC-19, San Jose, CA, 8 November 2011 15. 9° 14. 93° Creating more accurately angled screen 73/120

Limitation on supercell Periodic dot withdrawal pattern Abrupt texture change - Bayer structure Clustered-dot microcell with Bayer macrocell growing sequence Stochastic dot withdrawal pattern Homogeneous dot distribution Maze-like artifact Clustered-dot microscreen with stochastic-dispersed macrocell growing sequence CIC-19, San Jose, CA, 8 November 2011 74/120

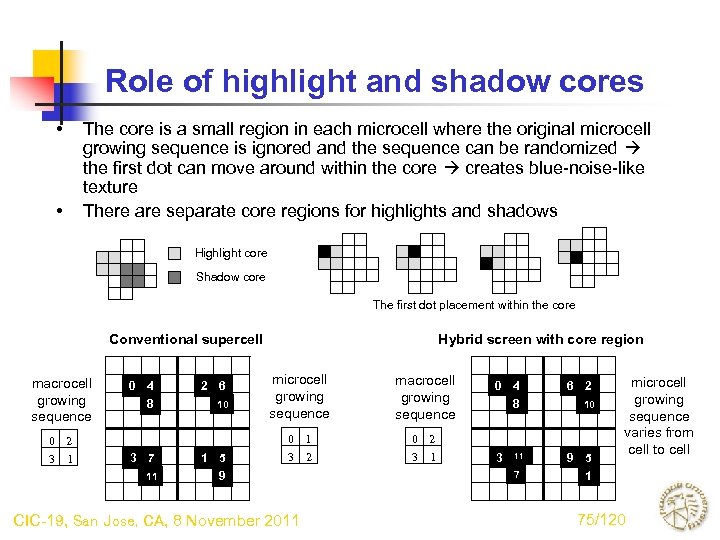Role of highlight and shadow cores • • The core is a small region in each microcell where the original microcell growing sequence is ignored and the sequence can be randomized the first dot can move around within the core creates blue-noise-like texture There are separate core regions for highlights and shadows Highlight core Shadow core The first dot placement within the core Conventional supercell macrocell growing sequence 0 2 3 1 0 4 8 3 7 11 2 6 10 1 5 9 Hybrid screen with core region microcell growing sequence macrocell growing sequence 0 1 3 2 0 2 3 1 CIC-19, San Jose, CA, 8 November 2011 0 4 8 6 2 3 9 5 1 11 7 10 microcell growing sequence varies from cell to cell 75/120

Improvement of texture quality with hybrid screen Clustered-dot microscreen with stochastic-dispersed macrocell growing sequence Stochastic dot withdrawal pattern Homogeneous dot distribution Maze-like artifact The hybrid screen – clustered-dot microcell with 2 x 2 core with DBS macrocell growing sequence No noticeable dot withdrawal pattern CIC-19, San Jose, CA, 8 November 2011 More homogeneous dot distribution No maze-like artifact 76/120

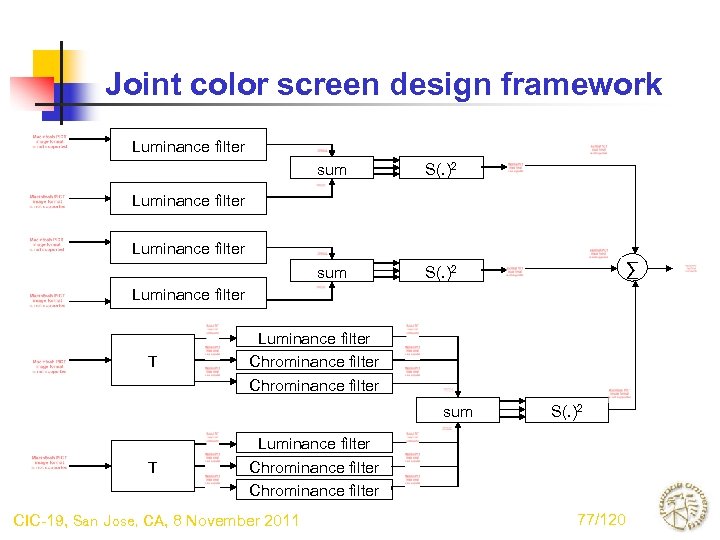Joint color screen design framework Luminance filter sum S(. )2 Luminance filter ∑ Luminance filter T Luminance filter Chrominance filter sum T S(. )2 Luminance filter Chrominance filter CIC-19, San Jose, CA, 8 November 2011 77/120

Joint screen design results Cyan halftone – plane independent screen design Cyan halftone – joint screen design with magenta screen CIC-19, San Jose, CA, 8 November 2011 78/120

Joint screen design results Magenta halftone – plane independent screen design Magenta halftone – joint screen design with cyan screen CIC-19, San Jose, CA, 8 November 2011 79/120

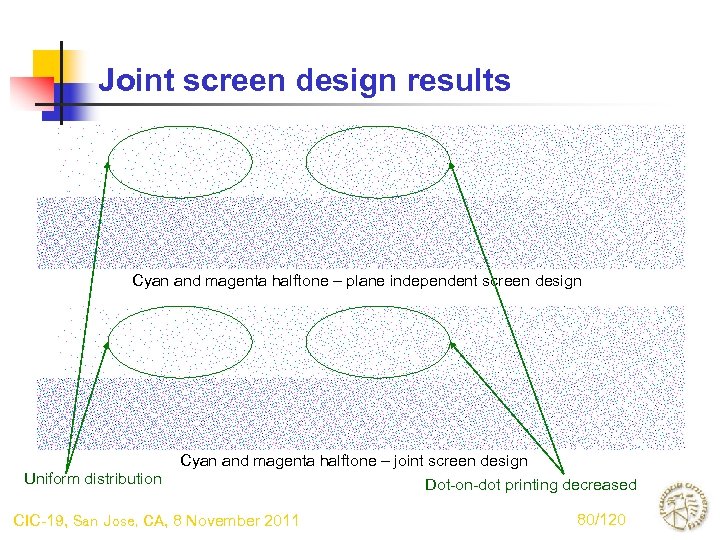Joint screen design results Cyan and magenta halftone – plane independent screen design Uniform distribution Cyan and magenta halftone – joint screen design Dot-on-dot printing decreased CIC-19, San Jose, CA, 8 November 2011 80/120

Synopsis of tutorial • General framework for spatiochromatic models for the HVS • Introduction to digital halftoning • Application of spatiochromatic models to design of color halftones - Embedding of spatiochromatic model within DBS for color halftoning - Use of spatiochromatic model with hybrid screen to improve highlight texture - Application of spatiochromatic model to design of tile sets for periodic clustered-dot screens • Overview of use of HVS models in image quality assessment • Color Image Fidelity Assessor CIC-19, San Jose, CA, 8 November 2011 81/120

Continuous Parameter Halftone Cell (CPHC) *F. Baqai and J. P. Allebach, Proc. IEEE, Jan. 2002 CIC-19, San Jose, CA, 8 November 2011 82/120

Finding Discrete Parameter Halftone Cell (DPHC) • Compute number of pixels in unit cell = |det(N)| • Assign pixels to unit cell in order of decreasing area of overlap with CPHC • Skip over pixels that are congruent to a pixel that has already been assigned to DPHC Area CIC-19, San Jose, CA, 8 November 2011 DPHC 83/120

Threshold Assignment by Growing Dots and Holes Simultaneously s[m] i[m] Abs. = 0. 26 Abs. = 0. 53 CIC-19, San Jose, CA, 8 November 2011 Abs. = 0. 74 84/120

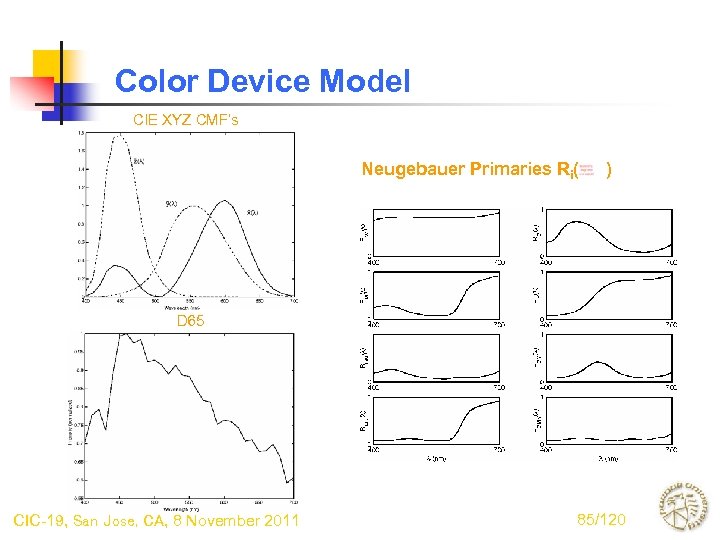Color Device Model CIE XYZ CMF’s Neugebauer Primaries Ri( ) D 65 CIC-19, San Jose, CA, 8 November 2011 85/120

Opponent Color Channels • Use linearized version of L*a* b* color space to represent opponent color channels of the human visual system Flohr et al [1993] CIC-19, San Jose, CA, 8 November 2011 86/120

Spatial Frequency Response of Opponent Channels Luminance [Nasanen] cyc les/ sam ple Chrominance [Kolpatzik and Bouman] e ampl cy cles/s CIC-19, San Jose, CA, 8 November 2011 cyc les/ sam ple e ampl s/s cycle 87/120

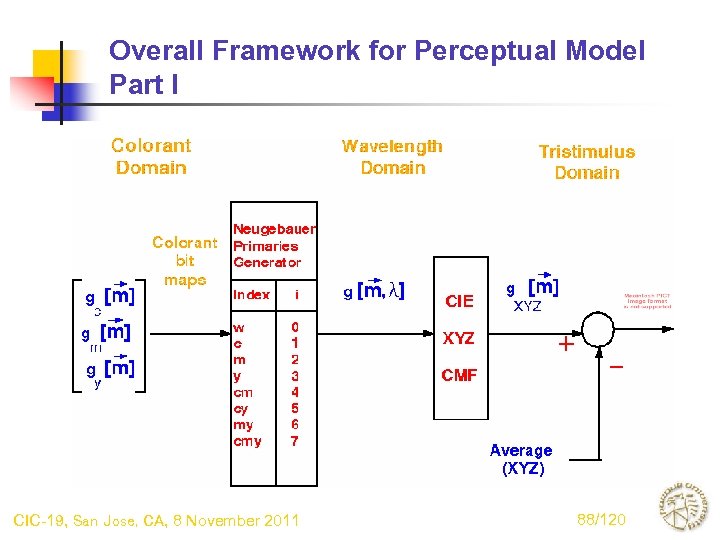Overall Framework for Perceptual Model Part I CIC-19, San Jose, CA, 8 November 2011 88/120

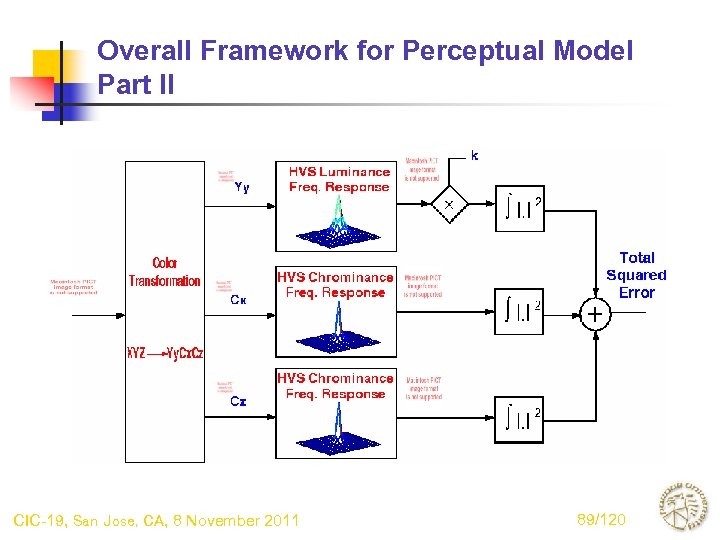Overall Framework for Perceptual Model Part II CIC-19, San Jose, CA, 8 November 2011 89/120

Magnified Scanned Textures for Various Screens Best Absorptance = 0. 25 Worst MSE = 9 x Best Optimized for Registration Errors MSE = 4 x Best CIC-19, San Jose, CA, 8 November 2011 Conventional MSE = 5 x Best 90/120

Weighted Spectra of Error in Yy. Cx. Cz Best CIC-19, San Jose, CA, 8 November 2011 Worst 91/120

Weighted Spectra of Error in Yy. Cx. Cz Optimized for Registration Errors CIC-19, San Jose, CA, 8 November 2011 Conventional 92/120

Synopsis of tutorial • General framework for spatiochromatic models for the HVS • Introduction to digital halftoning • Application of spatiochromatic models to design of color halftones • Overview of use of HVS models in image quality assessment • Color Image Fidelity Assessor CIC-19, San Jose, CA, 8 November 2011 93/120

An image quality example • Noise in low-light parts of scene • Moire on Prof. Bouman’s shirt • JPEG artifacts • Poor color rendering – too red • Poor contrast and tone – too dark • Glare from flash CIC-19, San Jose, CA, 8 November 2011 ”It's a little frightening to think that this picture is associated with the Transactions on Image Processing” – C. A. Bouman 94/120

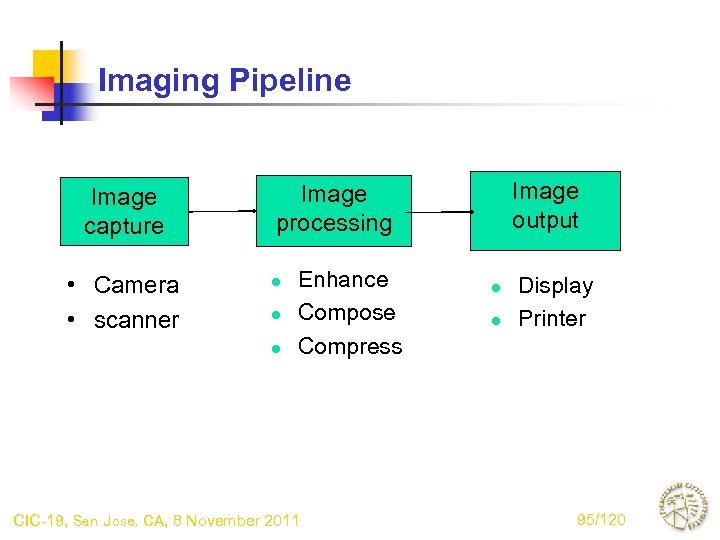Imaging Pipeline Image capture • Camera • scanner Image output Image processing l l l Enhance Compose Compress CIC-19, San Jose, CA, 8 November 2011 l l Display Printer 95/120

Image quality perspectives – image vs. system • Imaging systems based - Resolution (modulation transfer function) - Dynamic range - Noise characteristics • Image-based - Sharpness - Contrast - Graininess/mottle CIC-19, San Jose, CA, 8 November 2011 96/120

Image quality vs. print quality • Image quality - Broader viewpoint - Often focuses on issues that arise during image processing phase below, especially compression. - May also consider image capture and display • Print quality - Specifically considers issues that arise during printing Image capture Image processing CIC-19, San Jose, CA, 8 November 2011 Image output 97/120

Typical image quality issues • See discussion of photograph of Charles A. Bouman et al CIC-19, San Jose, CA, 8 November 2011 98/120

Typical print quality issues • Bands – orthogonal to process direction • Streaks – parallel to process direction • Spots - Repetitive - Random • • Color plane registration errors Ghosting Toner scatter Swath misalignment CIC-19, San Jose, CA, 8 November 2011 http: //www. hp. com/cpso-supportnew/pq/4700/home. html 99/120

Image quality assessment functionalities • Metrics vs. maps - Local or global strength of a particular defect – a single number - Map showing defect strength throughout the image – an image • Single defect vs. summative measures - Assess strength of a single defect, i. e. noise - Assess overall image quality – must account for all significant defects and their interactions • Reference vs. no-reference methods CIC-19, San Jose, CA, 8 November 2011 100/120

Image quality assessment factors • Masking – image content may mask visibility of defect - Texture - Edges • Tent-pole effect – worse defect dominates percept of image quality defects and overall assessment of image quality CIC-19, San Jose, CA, 8 November 2011 101/120

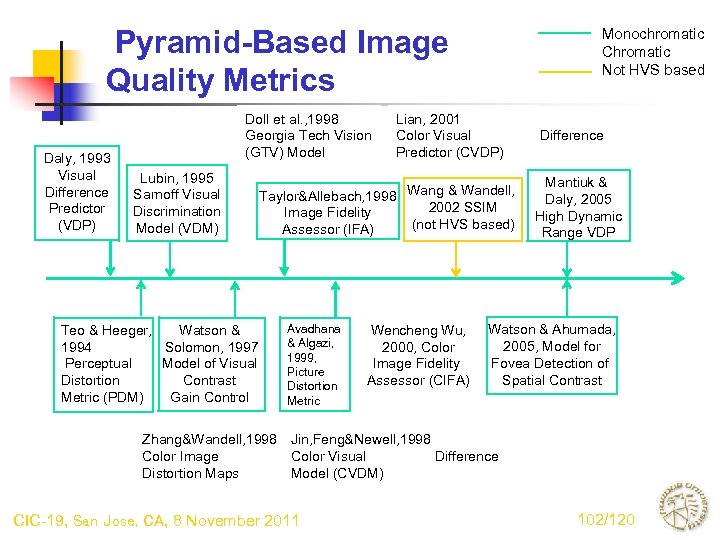Pyramid-Based Image Quality Metrics Daly, 1993 Visual Difference Predictor (VDP) Doll et al. , 1998 Georgia Tech Vision (GTV) Model Lubin, 1995 Sarnoff Visual Discrimination Model (VDM) Teo & Heeger, Watson & 1994 Solomon, 1997 Perceptual Model of Visual Distortion Contrast Metric (PDM) Gain Control Monochromatic Chromatic Not HVS based Lian, 2001 Color Visual Predictor (CVDP) Taylor&Allebach, 1998 Wang & Wandell, 2002 SSIM Image Fidelity (not HVS based) Assessor (IFA) Avadhana & Algazi, 1999, Picture Distortion Metric Wencheng Wu, 2000, Color Image Fidelity Assessor (CIFA) Difference Mantiuk & Daly, 2005 High Dynamic Range VDP Watson & Ahumada, 2005, Model for Fovea Detection of Spatial Contrast Zhang&Wandell, 1998 Jin, Feng&Newell, 1998 Color Image Color Visual Difference Distortion Maps Model (CVDM) CIC-19, San Jose, CA, 8 November 2011 102/120

Structural Similarity (SSIM) Index* • The SSIM Index expresses the similarity of image X and image Y at a point (i, j) where is a measure of local luminance similarity is a measure of local contrast similarity is a measure of local structure similarity *Wang & Bovik, IEEE Signal Processing Letters, March 02 *Wang, Bovik, Sheikh & Simoncelli, Trans on IP, March 04 CIC-19, San Jose, CA, 8 November 2011 103/120

Luminance similarity where, local average luminance window function or , the luminance of the pixel; A typical window is a 11 X 11 circular-symmetric Gaussian weighting function. CIC-19, San Jose, CA, 8 November 2011 104/120

Contrast similarity where or , the luminance of the pixel; A typical window is a 11 X 11 circular-symmetric Gaussian weighting function. CIC-19, San Jose, CA, 8 November 2011 105/120

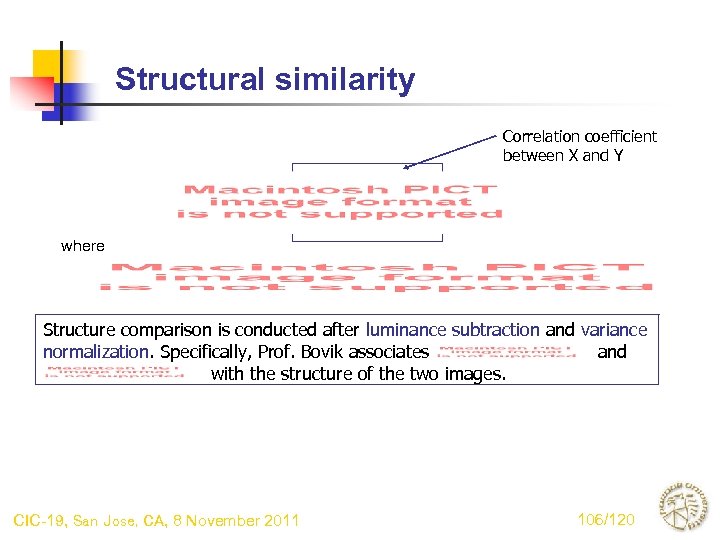Structural similarity Correlation coefficient between X and Y where Structure comparison is conducted after luminance subtraction and variance normalization. Specifically, Prof. Bovik associates and with the structure of the two images. CIC-19, San Jose, CA, 8 November 2011 106/120

Synopsis of tutorial • General framework for spatiochromatic models for the HVS • Introduction to digital halftoning • Application of spatiochromatic models to design of color halftones • Overview of use of HVS models in image quality assessment • Color Image Fidelity Assessor CIC-19, San Jose, CA, 8 November 2011 107/120

*C. Taylor, Z. Pizlo, and J. P. Allebach, IS&T PICS, May. 1998 * CIC-19, San Jose, CA, 8 November 2011 108/120

Model for assessment of color image fidelity • Color extension of Taylor’s achromatic IFA • The model predicts perceived image fidelity - Assesses visible differences in the opponent channels - Explains the nature of visible difference (luminance change vs. color shift) Ideal Rendered Color Image Fidelity Assessor (CIFA) *W. Wu, Z. Pizlo, and J. P. Viewing parameters Allebach, IS&T PICS, Apr. 2001 CIC-19, San Jose, CA, 8 November 2011 Image maps of predicted visible differences 109/120

Chromatic difference (Definition) • Objective: evaluate the spatial interaction between colors • First transform CIE XYZ to opponent color space (O 2, O 3) * Luminance Red-Green Blue-Yellow • Then normalize to obtain opponent chromaticities (o 2, o 3) • Define chromatic difference (analogous to luminance contrast c 1) * X. Zhang and B. A. Wandell, “A SPATIAL EXTENSION OF CIELAB FOR DIGITAL COLOR IMAGE REPRODUCTION”, SID-97 CIC-19, San Jose, CA, 8 November 2011 110/120

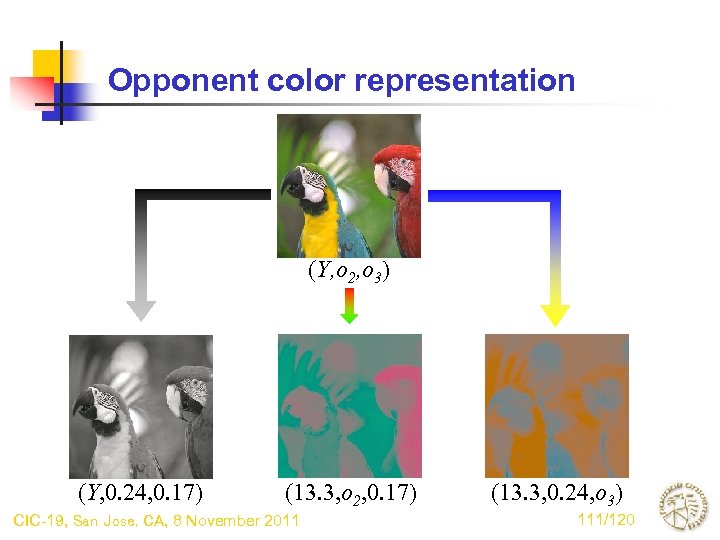Opponent color representation (Y, o 2, o 3) (Y, 0. 24, 0. 17) (13. 3, o 2, 0. 17) CIC-19, San Jose, CA, 8 November 2011 (13. 3, 0. 24, o 3) 111/120

Chromatic difference (illustration) 0. 1 • 0. 05 0. 2 0. 1 Chromatic difference is the amplitude of the sinusoidal grating • Chromatic difference is a measure of chromaticity variation • Chromatic difference is a spatial feature derived from opponent chromaticity that has little dependence upon luminance CIC-19, San Jose, CA, 8 November 2011 112/120

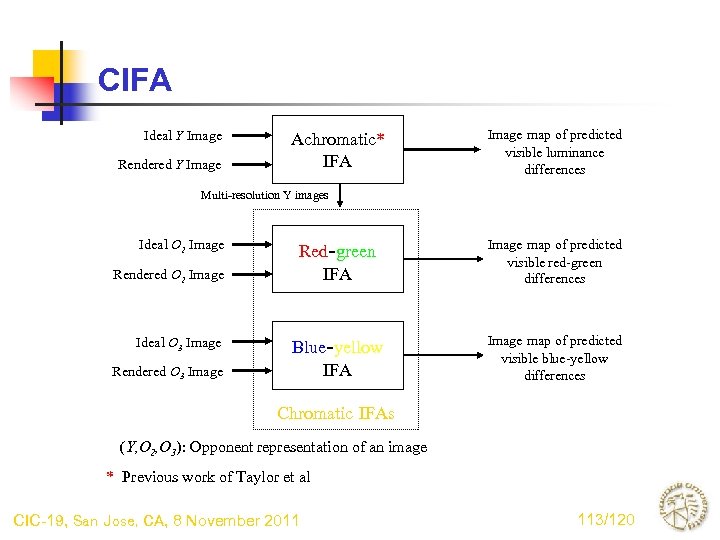CIFA Ideal Y Image Rendered Y Image Achromatic* IFA Image map of predicted visible luminance differences Multi-resolution Y images Ideal O 2 Image Rendered O 2 Image Ideal O 3 Image Rendered O 3 Image Red-green IFA Image map of predicted visible red-green differences Blue-yellow IFA Image map of predicted visible blue-yellow differences Chromatic IFAs (Y, O 2, O 3): Opponent representation of an image * Previous work of Taylor et al CIC-19, San Jose, CA, 8 November 2011 113/120

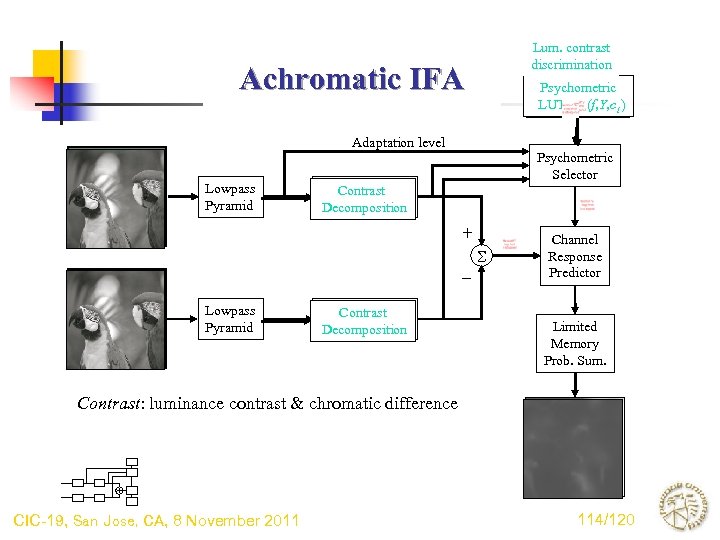Lum. contrast Chromatic diff. discrimination Psychometric LUT (f, Y, c ) LUT (f, o 2, c 21) Achromatic IFA Red-green IFA Adaptation level Lowpass Pyramid Psychometric Selector Chromatic Diff. Contrast Decomposition + S – Lowpass Pyramid Chromatic Diff. Contrast Decomposition Channel Response Predictor Limited Memory Prob. Sum. Contrast: luminance contrast & chromatic difference CIC-19, San Jose, CA, 8 November 2011 114/120

Estimating parameters of LUT (Psychophysical method) Probability of choosing left • Red-green stimulus: (Y, o 2, o 3) specifies the background color, c 2 is the ref. chromatic difference • Which stimulus has less chromatic difference? CIC-19, San Jose, CA, 8 November 2011 115/120

Representative results Blue-yellow discrimination at BY 1: (Y, o 2, o 3)=(5, 0. 3, 0. 2) Threshold Red-green discrimination at RG 1: (Y, o 2, o 3)=(5, 0. 2, -0. 3) Reference c 2 Reference c 3 • Results for f = 16, 8, 4, 2, 1 cycle/deg are drawn in red, green, blue, yellow, and black. • Threshold is not affected strongly by the reference chromatic difference • Chromatic channels function like low-pass filters CIC-19, San Jose, CA, 8 November 2011 116/120

CIFA output for example distortions (Hue change) Luminance CIC-19, San Jose, CA, 8 November 2011 R-G B-Y 117/120

CIFA output for example distortions (Blurring) Luminance CIC-19, San Jose, CA, 8 November 2011 R-G B-Y 118/120

CIFA output for example distortions (Limited gamut) Luminance CIC-19, San Jose, CA, 8 November 2011 R-G B-Y 119/120

Thank you for your attention! CIC-19, San Jose, CA, 8 November 2011 120/120