Spatial Methods in Econometrics Daniela Gumprecht Department for

Spatial Methods in Econometrics Daniela Gumprecht Department for Statistics and Mathematics, University of Economics and Business Administration, Vienna

Content • • Spatial analysis – what for? Spatial data Spatial dependency and spatial autocorrelation Spatial models Spatial filtering Spatial estimation R&D Spillovers 2

Spatial data – what for? • Exploitation of regional dependencies (information spillover) to improve statistical conclusions. • Techniques from geological and environmental sciences. • Growing number of applications in social and economic sciences (through the dispersion of GIS). 3

Spatial data • Spatial data contain attribute and locational information (georeferenced data). • Spatial relationships are modelled with spatial weight matrices. • Spatial weight matrices measure similarities (e. g. neighbourhood matrices) or dissimilarities (distance matrices) between spatial objects. 4

Spatial dependency • “Spatial dependency is the extent to which the value of an attribute in one location depends on the values of the attribute in nearby locations. ” (Fotheringham et al, 2002). • “Spatial autocorrelation (…) is the correlation among values of a single variable strictly attributable to the proximity of those values in geographic space (…). ” (Griffith, 2003). • Spatial dependency is not necessarily restricted to geographic space 5

Spatial weight matrices • • • W = [wij], spatial link matrix. wij = 0 if i = j wij > 0 if i and j are spatially connected If w*ij = wij / Σj wij, W* is called row-standardized W can measure similarity (e. g. connectivity) or dissimilarity (distances). • Similarity and dissimilarity matrices are inversely related – the higher the connectivity, the smaller the distance. 6

Spatial stochastic processes • Spatial autoregressive (SAR) processes. • Spatial moving average (SMA) processes. • Spatial lag operator is a weighted average of random variables at neighbouring locations (spatial smoother): Wy W n n spatial weights matrix y n 1 vector of observations on the random variable Elements W: non-stochastic and exogenous 7

SAR and SMA processes • Simultaneous SAR process: y = ρWy+ε = (I-ρW)-1ε • Spatial moving average process: y = λWε+ε = (I+λW)ε y centred variable I n n identity matrix ε i. i. d. zero mean error terms with common variance σ² ρ, λ autoregressive and moving average parameters, in most cases |ρ|<1. 8

SAR and SMA processes • Variance-covariance matrix for y is a function of two parameters, the noise variance σ² and the spatial coefficient, ρ or λ. • SAR structure: Ω(ρ) = Cov[y, y] = E[yy’] = σ²[(I-ρW)’(I-ρW)]-1 • SMA structure: Ω(λ) = Cov[y, y] = E[yy’] = σ²(I+ λW)’ 9

Spatial regression models • Spatial lag model: Spatial dependency as an additional regressor (lagged dependent variable Wy) y = ρWy+Xβ+ε • Spatial error model: Spatial dependency in the error structure (E[uiuj] ≠ 0) y = Xβ+u and u = ρWu+ε y = ρWy+Xβ-ρWXβ+u Spatial lag model with an additional set of spatially lagged exogenous variables WX. 10

Moran‘s I • Measure of spatial autocorrelation: I = e’(1/2)(W+W’)e / e’e e vector of OLS residuals • E[I] = tr(MW) / (n-k) • Var[I] = tr(MWMW’)+tr(MW)²+tr((MW))² / (n-k)(n-k+2)–[E(I)]² M = I-X(X’X)-1 X’ projection matrix 11

Test for spatial autocorrelation • One-sided parametric hypotheses about the spatial autocorrelation level ρ H 0: ρ ≤ 0 against H 1: ρ > 0 for positive spatial autocorrelation. H 0: ρ ≥ 0 against H 1: ρ < 0 for negative spatial autocorrelation. • Inference for Moran’s I is usually based on a normal approximation, using a standardized zvalue obtained from expressions for the mean and variance of the statistic. z(I) = (I-E[I])/√Var[I] 12

Spatial filtering • Idea: Separate regional interdependencies and use conventional statistical techniques that are based on the assumption of spatially uncorrelated errors for the filtered variables. • Spatial filtering method based on the local spatial autocorrelation statistic Gi by Getis and Ord (1992). 13

Spatial filtering • Gi(δ) statistic, originally developed as a diagnostic to reveal local spatial dependencies that are not properly captured by global measures as the Moran’s I, is the defining element of the first filtering device • Distance-weighted and normalized average of observations (x 1, . . . , xn) from a relevant variable x. Gi(δ) = Σjwij(δ)xj / Σjxj, i ≠ j • Standardized to corresponding approximately Normal (0, 1) distributed z-scores z. Gi, directly comparable with well-known critical values. 14

Spatial filtering • Expected value of Gi(δ) (over all random permutations of the remaining n-1 observations) E[Gi(δ)] = Σjwij(δ) / (n-1) represents the realization at location i when no autocorrelation occurs. • Its ratio to the observed value indicates the local magnitude of spatial dependence. • Filter the observations by: xi* = xi[Σjwij(δ) / (n-1)] / Gi(δ) 15

Spatial filtering • (xi-xi*) purely spatial component of the observation. • xi* filtered or “spaceless” component of the observation. • If δ is chosen properly the z. Gi corresponding to the filtered values xi* will be insignificant. • Applying this filter to all variables in a regression model isolates the spatial correlation into (xixi * ). 16

Spatial estimation • S 2 SLS (from Kelejian and Prucha, 1995). It consists of IV or GMM estimator of the auxiliary parameters: (ρ , σ ²) = Arg min {[Γ(ρ, ρ², σ²)-γ]’[Γ(ρ, ρ², σ²) -γ]} with Ω =Ω(ρ , σ ²) = σ ²[I-W(ρ )]-1[I-W(ρ )’]-1 where ρ [-a, a], σ² [0, b] FGLS estimator: β FGLS = [X’Ω -1 X]-1 X’Ω -1 y 17

R&D Spillovers • Theories of economic growth that treat commercially oriented innovation efforts as a major engine of technological progress and productivity growth (Romer 1990; Grossman and Helpman, 1991). • Coe and Helpman (1995): productivity of an economy depends on its own stock of knowledge as well as the stock of knowledge of its trade partners. 18

R&D Spillovers • Coe and Helpman (1995) used a panel dataset to study the extent to which a country’s productivity level depends on domestic and foreign stock of knowledge. • Cumulative spending for R&D of a country to measure the domestic stock of knowledge of this country. • Foreign stock of knowledge: import-weighted sum of cumulated R&D expenditures of the trade partners of the country. 19

R&D Spillovers • Panel dataset with 22 countries (21 OECD countries plus Israel) during the period from 1971 to 1990. • Variables total factor productivity (TFP), domestic R&D capital stock (DRD) and foreign R&D capital stock (FRD) are constructed as indices with basis 1985 (1985=1). • Panel data model with fixed effects. 20

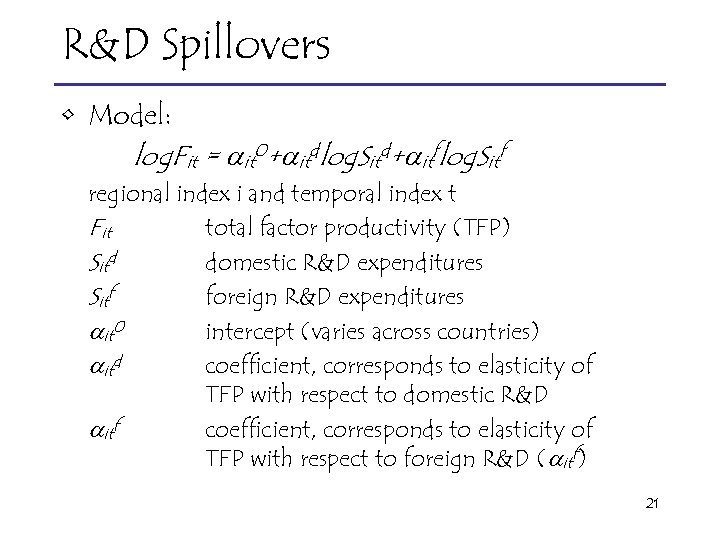R&D Spillovers • Model: log. Fit = it 0+ itdlog. Sitd+ itflog. Sitf regional index i and temporal index t Fit total factor productivity (TFP) Sitd domestic R&D expenditures Sitf foreign R&D expenditures it 0 intercept (varies across countries) itd coefficient, corresponds to elasticity of TFP with respect to domestic R&D itf coefficient, corresponds to elasticity of TFP with respect to foreign R&D ( itf) 21

R&D Spillovers • Assumption: variables R&D spending are spatially autocorrelated => no need to use separate variables for domestic and foreign R&D spendings. • Trade intensity: average of bilateral import shares between two countries = connectivity- or distance measure. 22

R&D Spillovers • The bilateral trade intensity between country i and j: w ij = (bij+bji)/2 w ij = 0 for i = j • bij are the bilateral import shares of country i from country j 23

R&D Spillovers • Distance between two countries: inverse connectivity 1 / w ij • The higher the connectivity the smaller the distance and vice versa. dij = wi j-1 for all i and j dii = 0 • Distance matrix D: symmetric n n matrix (231 distances for n = 22). 24

R&D Spillovers • Plot the distances between all countries. • Project all 231 distances from IR 21 to IR 2. • Minimize the sum of squared distances between the original points and the projected points: minx, y Σi(di-di. P)2 xnx 1, ynx 1 coordinates of points di original distances di. P distances in the projection space IR 2 25

R&D Spillovers 26

R&D Spillovers 27

R&D Spillovers • C&H results: using a standard fixed effects panel regression they yielded log. Fit = it 0+0, 097 log. Sitd+0, 0924 log. Sitf (10, 6836)*** (5, 8673)*** • Domestic and foreign R&D expenditures have a positive effect on total factor productivity of a country. 28

R&D Spillovers • Results using a dynamic random coefficients model: log. Fit = it 0+0, 3529 log. Sitd-0, 085 log. Sitf (7, 7946)*** (-1, 1866) • Domestic R&D expenditures have a positive effect on total factor productivity of a country, foreign R&D spending have no effect. 29

R&D Spillovers • Spatial analysis: standard fixed effects model with a spatial lagged exogenous variable: • log. Fit = it 0+0, 0673 Sitd+0, 1787 bijt. Sitd (4, 1483)*** (8, 2235)*** • Domestic and foreign R&D expenditures have a positive effect on total factor productivity of a country. 30

R&D Spillovers • Spatial analysis: dynamic random coefficients model with a spatially lagged exogenous variable: log. Fit = it 0+0, 1252 Sitd+0, 1663 bijt. Sitd (2, 2895)** (2, 1853)** • Domestic and foreign R&D expenditures have a positive effect on total factor productivity of a country. 31

R&D Spillovers • Conclusion: • Different estimation techniques lead to different results • Still not clear whether foreign R&D spending have an influence on total factor productivity. • Further research needed 32