Spatial Meaning and Quantification Yoad Winter Technion Utrecht

Spatial Meaning and Quantification Yoad Winter – Technion/Utrecht (Joint work with Sela Mador-Haim – Technion/UPenn) April 8, 2008 – Frankfurt SALT paper downloadable at: www. cs. technion. ac. il/~winter 1

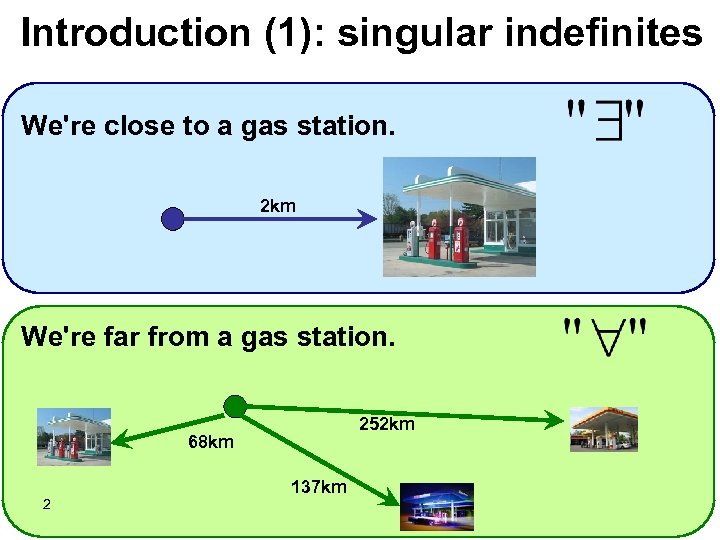Introduction (1): singular indefinites We're close to a gas station. 2 km We're far from a gas station. 252 km 68 km 2 137 km

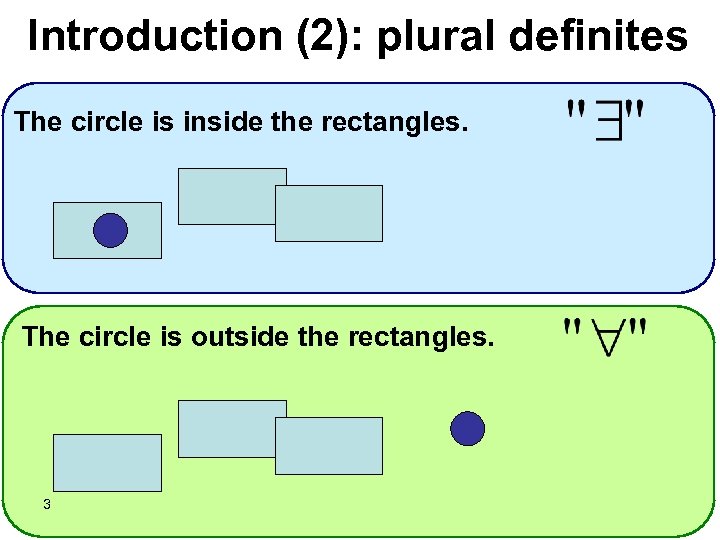Introduction (2): plural definites The circle is inside the rectangles. The circle is outside the rectangles. 3

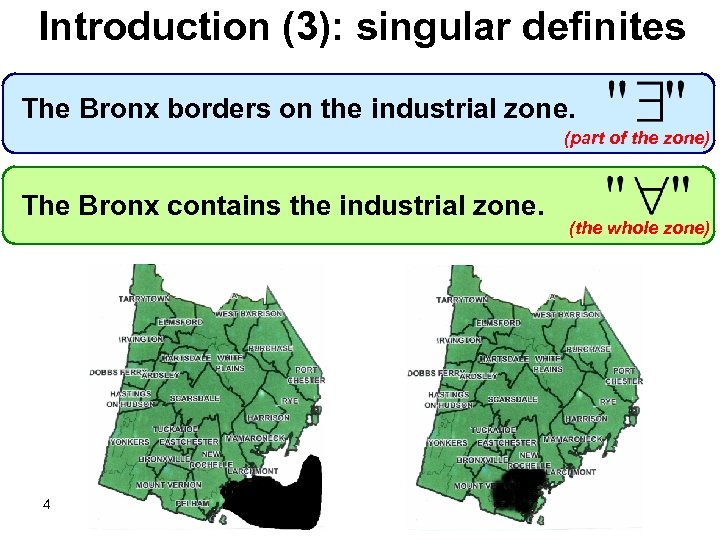Introduction (3): singular definites The Bronx borders on the industrial zone. (part of the zone) The Bronx contains the industrial zone. 4 (the whole zone)

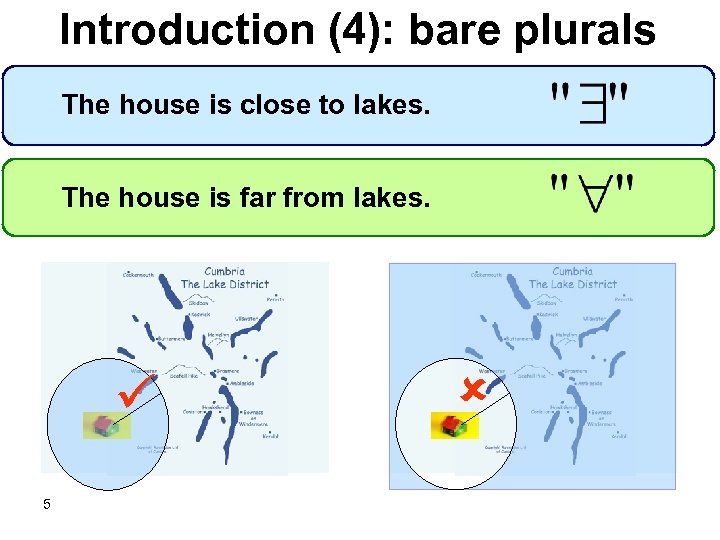Introduction (4): bare plurals The house is close to lakes. The house is far from lakes. 5

Empirical conclusion The identity of the spatial preposition affects (pseudo)-quantificational effects with: - Singular indfinites - Bare plurals - Singular and plural definites Which mechanisms govern this behavior? 6

Mechanism 1: Spatial Meaning of Preposition [[ outside(the lake) ]] = area outside the eigenspace of the lake 7 outside the lake

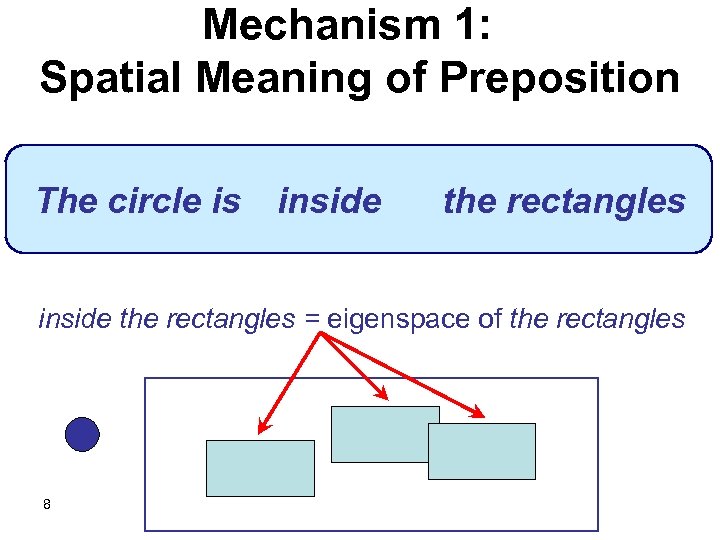Mechanism 1: Spatial Meaning of Preposition The circle is inside the rectangles = eigenspace of the rectangles 8

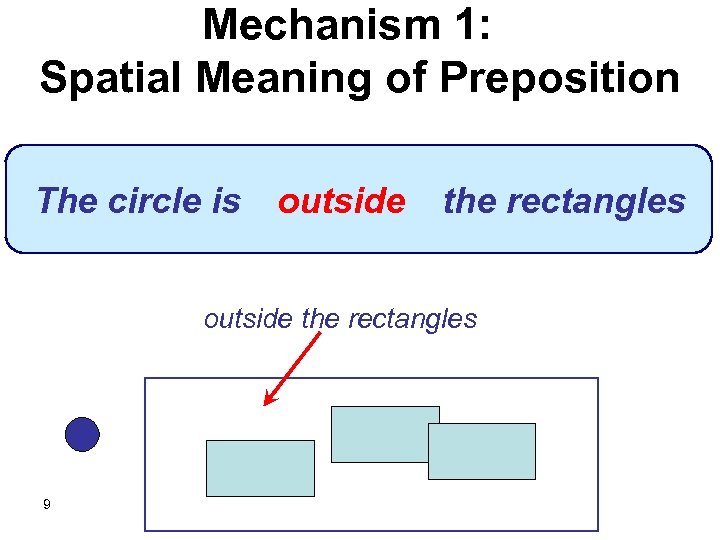Mechanism 1: Spatial Meaning of Preposition The circle is outside the rectangles 9

Mechanism 2: Semantic Incorporation [[ outside(a lake) ]] = area outside the eigenspace of the property for a lake eigenspace of “a lake” 10 outside a lake

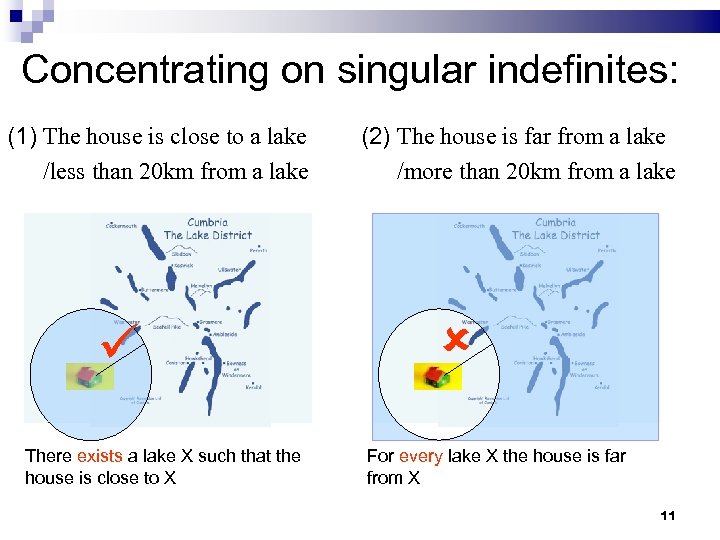Concentrating on singular indefinites: (1) The house is close to a lake /less than 20 km from a lake There exists a lake X such that the house is close to X (2) The house is far from a lake /more than 20 km from a lake For every lake X the house is far from X 11

Questions Which prepositions display non-existential effects with singular indefinites? Locative and temporal Not upward monotone Which singular indefinites? Predicative indefinites (a vs. some) What’s “Semantic Incorporation”? Zimmermann, Mc. Nally, Van Geenhoven, and others: a mechanism that allows predicative (property denoting) indefinites to become 12 arguments of other predicates.

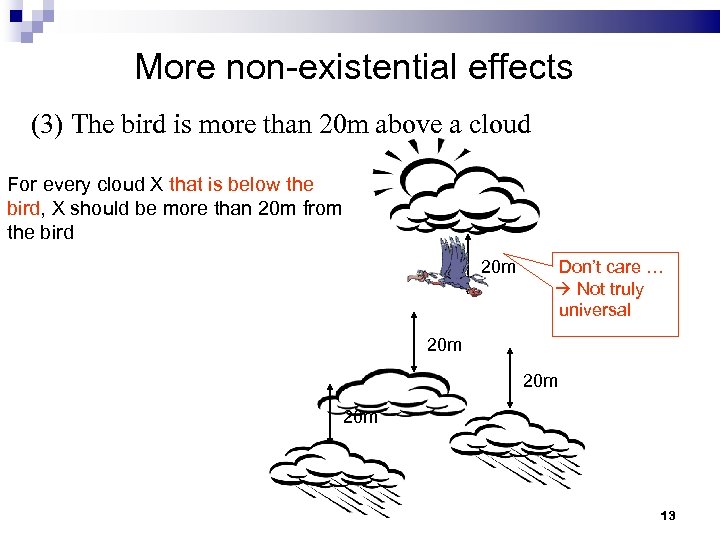More non-existential effects (3) The bird is more than 20 m above a cloud For every cloud X that is below the bird, X should be more than 20 m from the bird 20 m Don’t care … Not truly universal 20 m 20 m 13

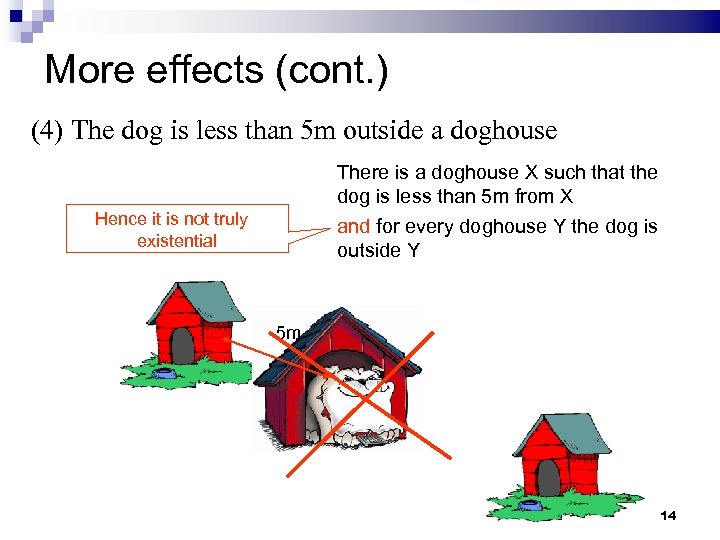More effects (cont. ) (4) The dog is less than 5 m outside a doghouse There is a doghouse X such that the dog is less than 5 m from X and for every doghouse Y the dog is outside Y Hence it is not truly existential 5 m 14

More effects (cont. ) (5) The house is (exactly) 100 m from a lake There is a lake X such that the house is exactly 100 m from X and for every lake Y the house is at least 100 m from Y 100 m 15

Conclusion from examples There is a broad spectrum of quantificational effects that are sensitive to the prepositional structure in use (1) The house is close to a lake (existential) (2) The house is far from a lake (universal) (3) The bird is more than 20 m above a cloud (semi-universal) (4) The dog is less than 5 m outside a doghouse (semi-existential) (5) The house is (exactly) 100 m from a lake (combination) What kind of mechanism can account for the different quantificational effects in (1)-(5)? 16

Proposed solution A predicative denotation of the indefinite A building: x. building(x) Locatives take such predicates as arguments semantic incorporation 17

Semantic incorporation Motivation: narrow scope of indefinites Obligatory narrow scope: There sentences (Mc. Nally 1992, 1998): There isn't a cloud in the sky Transitive constructions in West-Greenlandic (Van Geenhoven 1998): John fish-buy-NEG-IND-[tr]-3 sg ( / * ) Optional narrow scope as opposed to other NPs (Zimmermann 1993, Van Geenhoven and Mc. Nally 2005) John is looking for a dog/every dog Claim: Also in PPs, non-existential indefinites appear due to narrow scope via incorporation 18

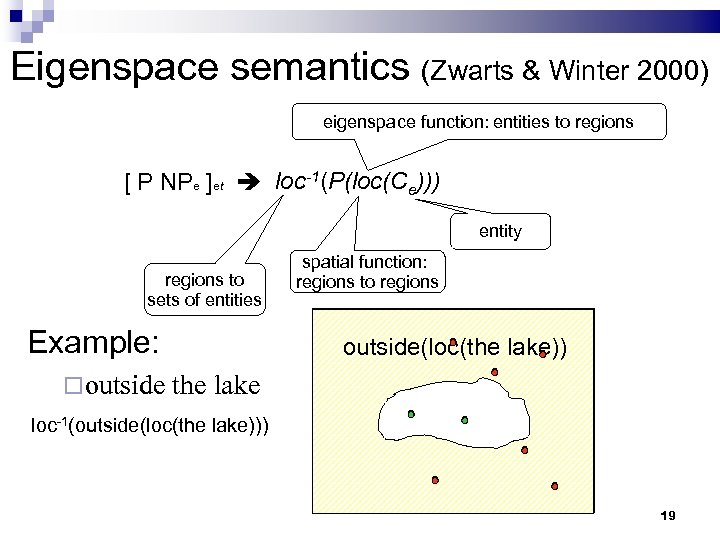Eigenspace semantics (Zwarts & Winter 2000) eigenspace function: entities to regions [ P NPe ]et loc-1(P(loc(Ce))) entity regions to sets of entities Example: outside spatial function: regions to regions outside(loc(the lake)) the lake loc-1(outside(loc(the lake))) loc(the lake) 19

Semantic incorporation of PPs Entity denoting (Zwarts and Winter): loc-1(P(loc(Ce))) The house is far from some lake bird is more than 50 above every cloud Predicative: loc-1(P(loc'(Cet))) The house is far from a lake The airplane is more than 20 m from mountains loc'(Cet) = x Cloc(x) 20

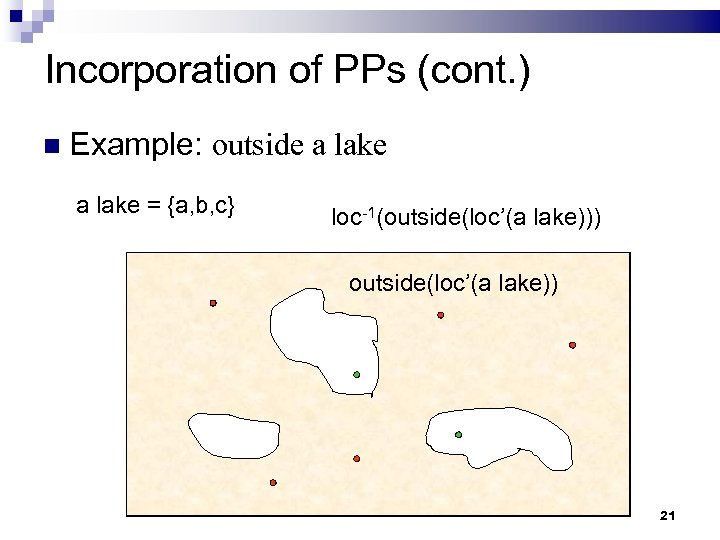Incorporation of PPs (cont. ) Example: outside a lake = {a, b, c} loc-1(outside(loc’(a lake))) outside(loc’(a lake)) loc’(a lake) b a c 21

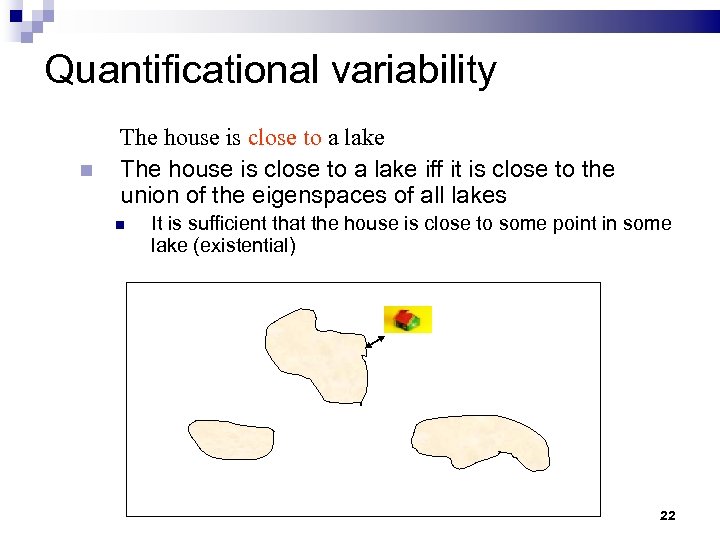Quantificational variability The house is close to a lake iff it is close to the union of the eigenspaces of all lakes It is sufficient that the house is close to some point in some lake (existential) 22

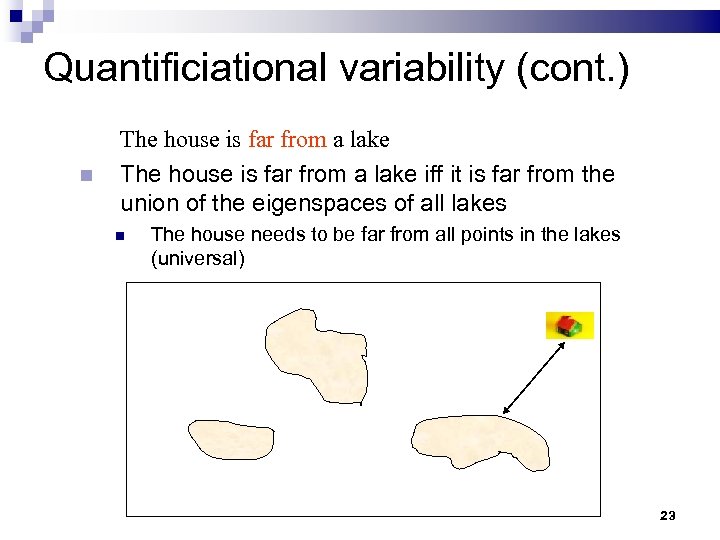Quantificiational variability (cont. ) The house is far from a lake iff it is far from the union of the eigenspaces of all lakes The house needs to be far from all points in the lakes (universal) 23

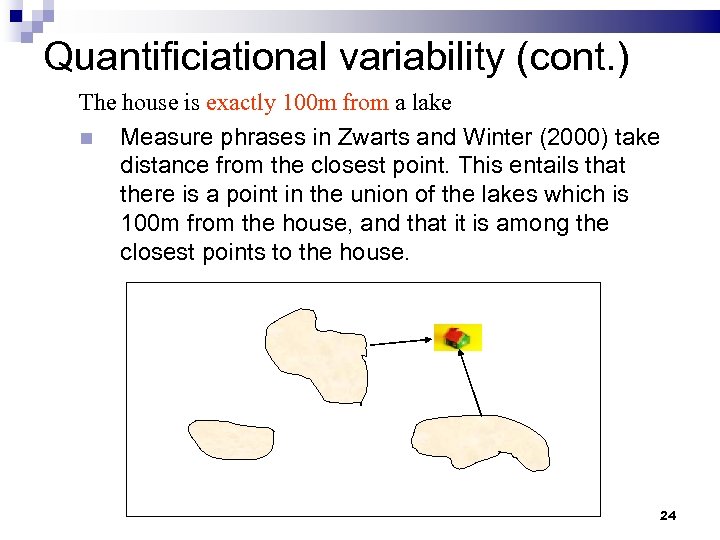Quantificiational variability (cont. ) The house is exactly 100 m from a lake Measure phrases in Zwarts and Winter (2000) take distance from the closest point. This entails that there is a point in the union of the lakes which is 100 m from the house, and that it is among the closest points to the house. 24

Quantificiational variability (cont. ) The dog is less than 5 m outside a doghouse Less than 5 m from the union of the eigenspaces of the doghouses, and not in that area 25

Point monotonicity (Zwarts and Winter) Which prepositions support existential B quantification? Only upward monotone Ps! A P is upward monotone if for all eigenspaces A, B s. t. A B: x P A x P B. Examples: inside, close to Similarly, only prepositions that are downward monotone lead to universal interpretation Examples: outside, far from 26 x

Downward Monotonicity – standard tests Downward/Upward entailing environments: The house is far from a lake The house is far from a small lake The house is close to a lake The house is close to a small lake NPI licensing (6) The house is far from/*close to any lake Not accounted for if PPs take entity arguments! 27

Other PPs Analogous effects with temporal PPs: (6) This shelter was built less than 2 years after a war Existential (7) This shelter was built more than 2 years after a war Semi-universal: similar to more than 2 meters above a cloud NPI licensing: before/*after any war Conclusion: temporal PPs can likewise incorporate their complement Directional PPs do not incorporate (thanks to J. Zwarts): (8) We went around a lake - (existential only) 28

Summary and conclusions Prepositions with indefinite complements exhibit a wide spectrum of quantificational variability A result of incorporation between predicative indefinites and prepositions Preposition monotonicity governs existential-universal variability Monotonicity is also verified by standard tests (NPI licensing, entailment) Incorporation – a general process with both locative and temporal prepositions 29

References Mc. Nally, L. 1992. An Interpretation for the English Existential Construction. Ph. D. Diss. , UCSC. Published 1997. Garland, New York Mc. Nally, L. 1998. Existential sentences without existential quantification. Linguistics and Philosophy 21, 353 -392 Mc. Nally, L. and V. Van Geenhoven 2005. On the property analysis of opaque complements. Lingua 115, 885 -914. Van Geenhoven, V. 1998. Semantic Incorporation and Indefinite Descriptions. CSLI Publications. Zimmermann, T. E. 1993. On the proper treatment of opacity in certain verbs. Natural Language Semantics 1, 149 -179. Zwarts, J. and Y. Winter 2000. Vector space semantics. Journal of Logic, Language and Information, 171 -213. 30