dbdb3df3b854774498f82f69bae123d9.ppt
- Количество слайдов: 59
![Spatial Databases First law of geography [Tobler]: Everything is related to everything, but nearby Spatial Databases First law of geography [Tobler]: Everything is related to everything, but nearby](https://present5.com/presentation/dbdb3df3b854774498f82f69bae123d9/image-1.jpg)
Spatial Databases First law of geography [Tobler]: Everything is related to everything, but nearby things are more related than distant things. Lecture 8 : Spatial Statistics Autocorrelation & Moran’s I Pat Browne

Statistical Spatial Data • In this lecture we consider spatial data contains an attribute e. g. house prices, occurrences of disease, occurrences of accidents, crop yield, poverty patterns, crime rates, etc. Earlier parts of the course covered the vector representation of physical objects such as houses, counties, and roads. These objects were arranged by theme. Here we consider attributes of those objects e. g. the population of an ED.

Spatial Statistics • Spatial statistics is the statistical study of spatial data that varies over discrete space e. g. crime rates broken down by neighbourhood. Spatial statistical models can be used for estimation, description, and prediction based on probability theory (not covered).
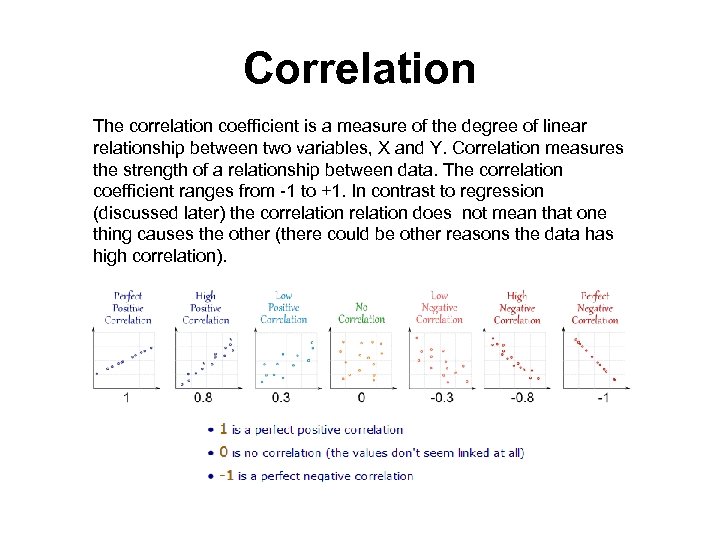
Correlation The correlation coefficient is a measure of the degree of linear relationship between two variables, X and Y. Correlation measures the strength of a relationship between data. The correlation coefficient ranges from -1 to +1. In contrast to regression (discussed later) the correlation does not mean that one thing causes the other (there could be other reasons the data has high correlation).
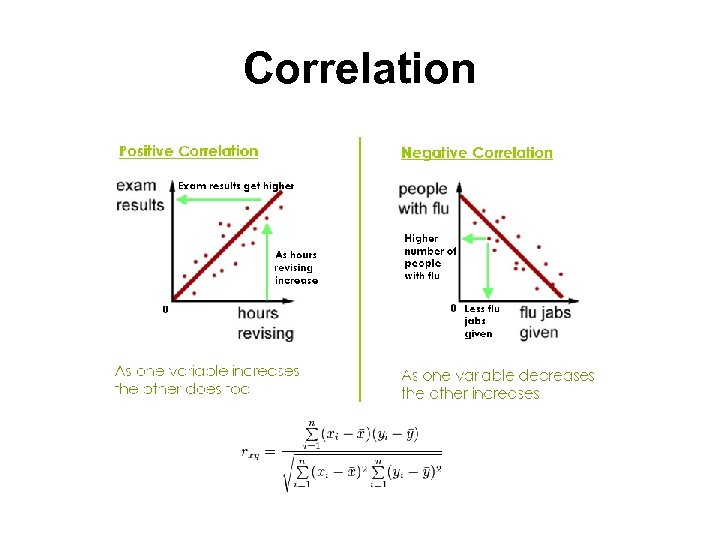
Correlation
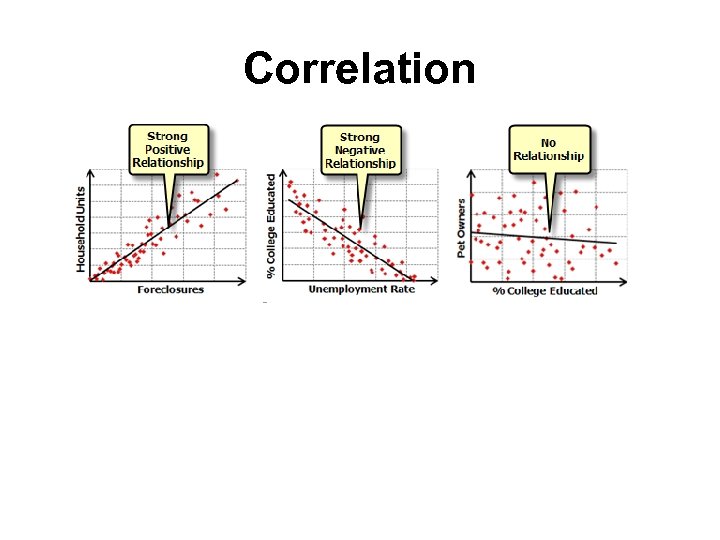
Correlation

Regression • Regression: takes a numerical dataset and develops a mathematical formula that fits the data. The results can be used to predict future behaviour. Works well with continuous quantitative data like weight, speed or age. Not good for categorical data where order is not significant, like colour, name, gender, nest/no nest. Example: plotting snowfall against height above sea level.
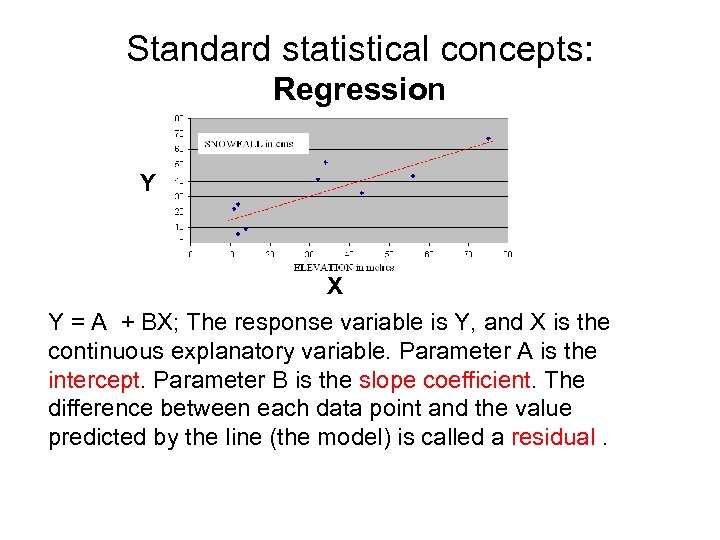
Standard statistical concepts: Regression Y X Y = A + BX; The response variable is Y, and X is the continuous explanatory variable. Parameter A is the intercept. Parameter B is the slope coefficient. The difference between each data point and the value predicted by the line (the model) is called a residual.

Regression Y X Where X , Y are the means of X and Y. Alternative terminology for linear regression equation: Y = a + b. X where • Y is the dependent variable • a is the intercept • b is the slope or regression coefficient • X is the independent variable

Standard statistical concepts: i. i. d • A collection of two or more random variables {X 1, X 2, … , } is independent and identically distributed (i. i. d) if the variables have the same probability distribution, and are independent. For example tossing a coin several times. For every coin, the probability is the same. This is known as identical probability for each coin. Also, each toss is independent i. e. how one coin lands does not determine how another coin lands.

Standard statistical concepts: Examples • Example i. i. d: All other things being equal, a sequence of dice rolls is i. i. d. • Example of non i. i. d: bird nesting patterns in wetlands, where the independent variables are distance from water, length of grass, depth of water and the dependent variable would be the presence of a nest site. A uniform distribution of these variables on a map would indicate an even distribution, however a more complex emerges where the variables are spatially dependent.
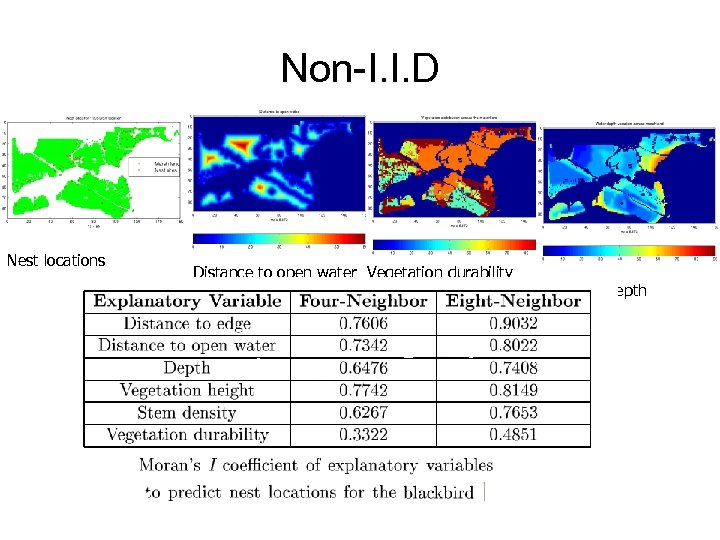
Non-I. I. D Nest locations Distance to open water Vegetation durability Water depth
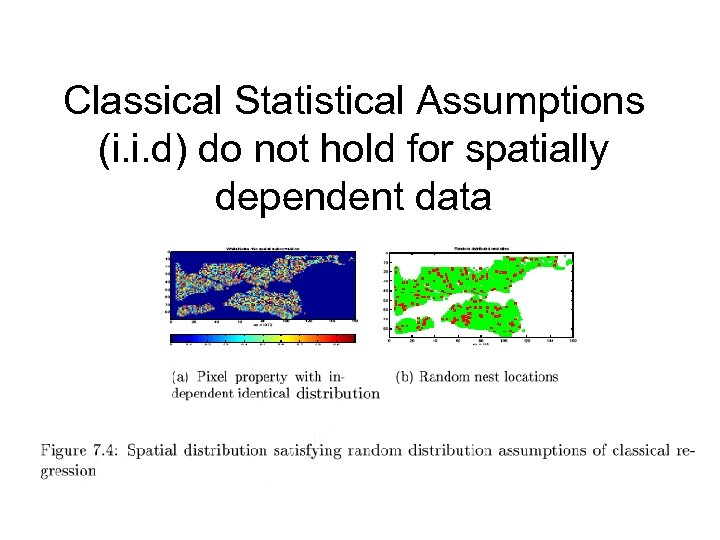
Classical Statistical Assumptions (i. i. d) do not hold for spatially dependent data

Standard statistical concepts: Correlation • Correlation: A correlation is a single number that describes the degree of relationship between two normally distributed variables. The variables are not designated as dependent or independent. The value of a correlation coefficient can vary from minus one to plus one. A minus one indicates a perfect negative correlation, while a plus one indicates a perfect positive correlation. A correlation of zero means there is no relationship between the two variables. When there is a negative correlation between two variables, as the value of one variable increases, the value of the other variable decreases, and vice versa.

Standard statistical concepts: Correlation • Correlation is a measure of the degree of linear relationship between two variables, say X and Y. While in regression the emphasis is on predicting one variable from the other, in correlation the emphasis is on the degree to which a linear model may describe the relationship between two variables. In regression the interest is directional, one variable is predicted and the other is the predictor; in correlation the interest is nondirectional, the relationship is the critical aspect. The correlation coefficient may take on any value between plus and minus one (-1 < r < 1).
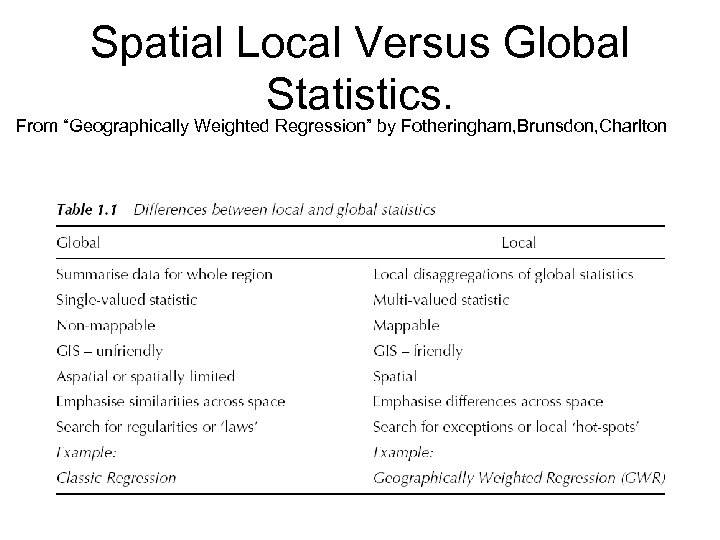
Spatial Local Versus Global Statistics. From “Geographically Weighted Regression” by Fotheringham, Brunsdon, Charlton

Local Versus Global Statistics. From “Geographically Weighted Regression” by Fotheringham, Brunsdon, Charlton

The ecological fallacy and the modifiable areal unit problem From “Spatial data analysis” by Christopher D. Lloyd We often need to use spatially aggregated data, for example census zones or cells in remotely sensed images. Such zones are unlikely to be internally homogeneous. A cell in a remotely sensed image has only one value, but in the real world there may be several features in the area covered by the cell. The variation within an area is lost if the area is larger than the individual features it contains.

Ecological fallacy/Modifi able areal unit problem(MAUP) From “Spatial data analysis” by Christopher D. Lloyd The ecological fallacy refers to the problem of making inferences about individuals from aggregate data. For example, not all people in one census zone are likely to share the same characteristics. The majority of people in a census zone may be wealthy, but if there is a housing estate (high density) just inside one edge of the zone then clearly generalizations about the population of the zone may be unsound.

Modifable areal unit problem(MAUP) From “Spatial data analysis” by Christopher D. Lloyd • The MAUP is composed of two parts: – The scale effect: Statistical analyses based on data aggregated over areas of different sizes will produce different results. – The zoning effect : Two sets of zones can have the same or similar areas but very different forms and analyses based on two such sets of zones may vary.
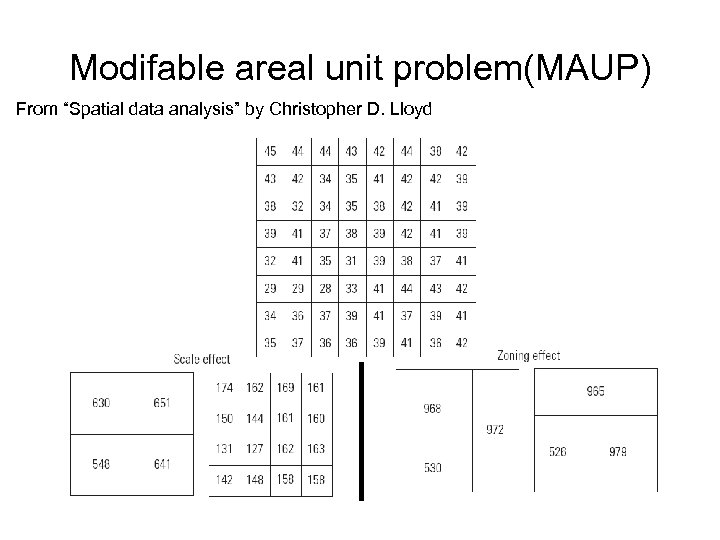
Modifable areal unit problem(MAUP) From “Spatial data analysis” by Christopher D. Lloyd

Modifable areal unit problem(MAUP) From “Spatial data analysis” by Christopher D. Lloyd

Moving Window From “Spatial data analysis” by Christopher D. Lloyd Moving windows (MW) map how values change from place to place. MW used in many contexts, including finding the gradient of the terrain locally

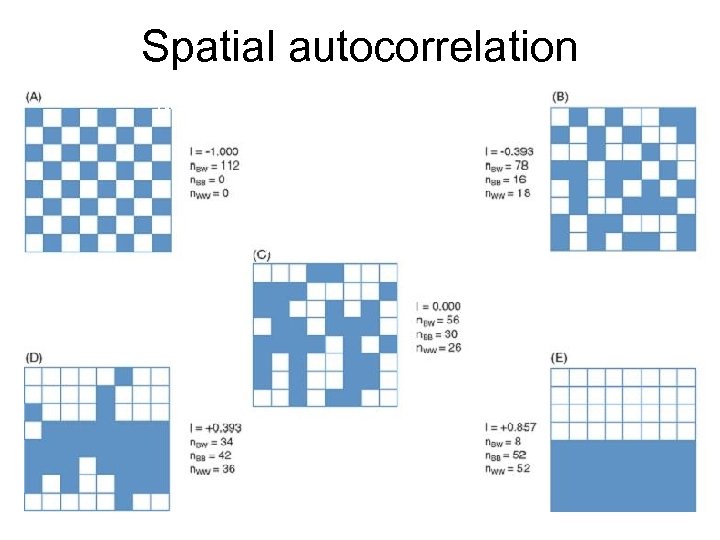
Spatial autocorrelation • Spatial autocorrelation (SA) is the degree of correlation between neighbouring values of some property of a region (e. g. population). SA occurs when the value of a variable in a location is correlated with values of the same variable in the neighbourhood. SA is measured with Moran’s I. • Moran’s I measures the average correlation between the value of a variable at one location and the value at nearby locations. The essential idea is to specify pairs of locations that influence each other along with the relative intensity of interaction. Moran’s I provides a global view of spatial autocorrelation.

Moran’s I • The range of the Moran's I statistic depends on the spatial weight matrix. • When Moran's I is scaled by its bounds the statistic is restricted to the range ± 1 • Moran’s I can serve as a tool for modeling spatial dependencies in many data mining techniques.
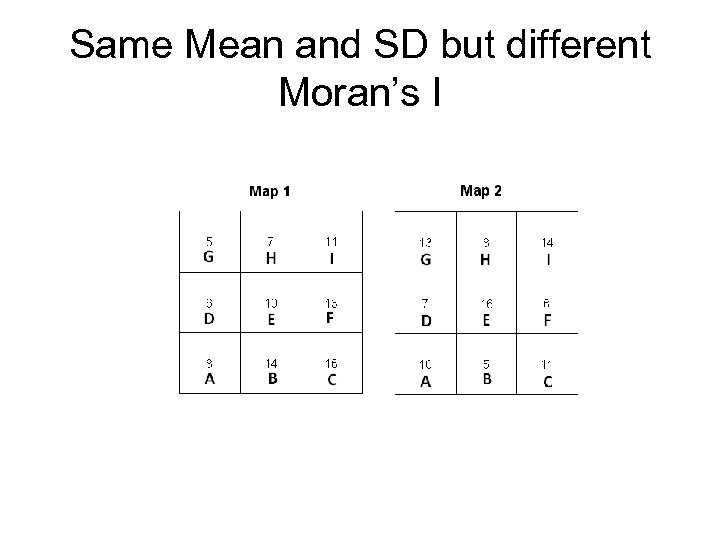
Same Mean and SD but different Moran’s I
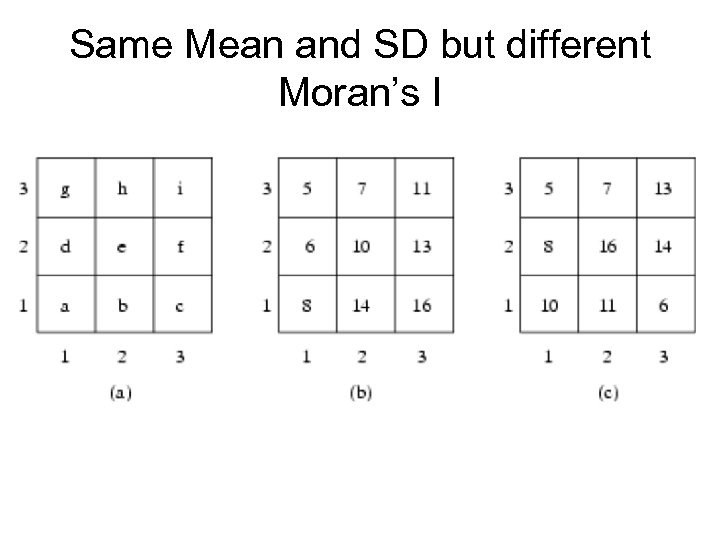
Same Mean and SD but different Moran’s I
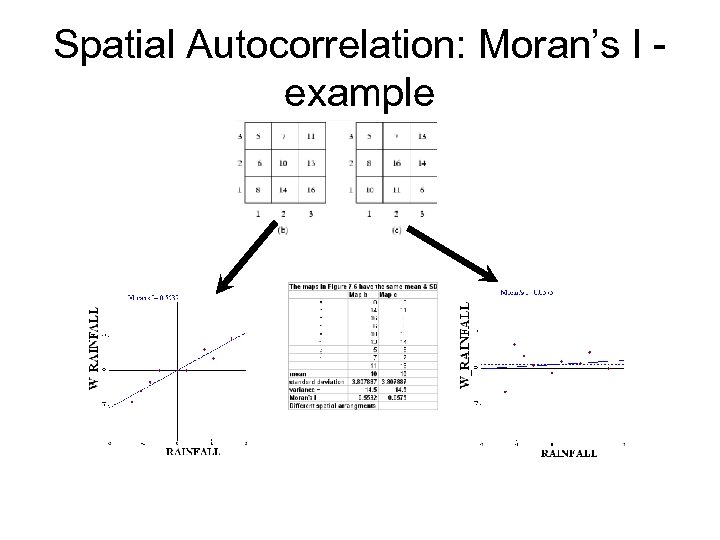
Spatial Autocorrelation: Moran’s I example

Moran’s I - example Figure 7. 5, pp. 190 • Pixel value set in (b) and (c ) are same but their Moran Is are different. • Q? Which dataset between (b) and (c ) has higher spatial autocorrelation?
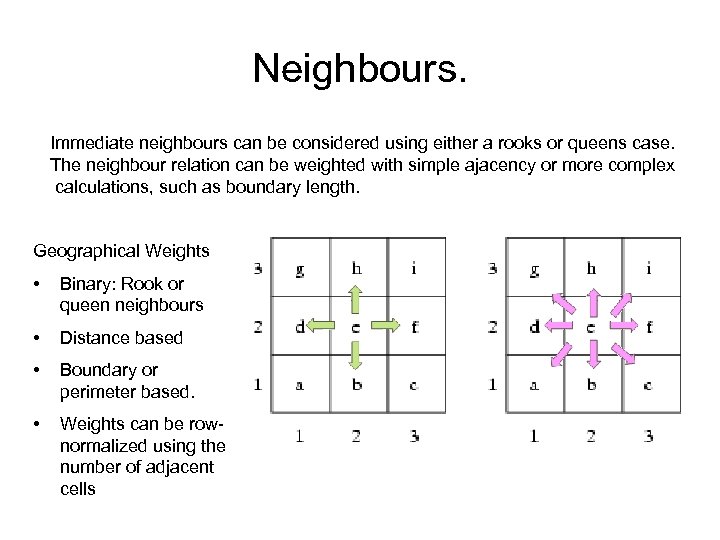
Neighbours. Immediate neighbours can be considered using either a rooks or queens case. The neighbour relation can be weighted with simple ajacency or more complex calculations, such as boundary length. Geographical Weights • Binary: Rook or queen neighbours • Distance based • Boundary or perimeter based. • Weights can be rownormalized using the number of adjacent cells

Neigbourhood relationship contiguity matrix

Spatial Lag Example 1 2 7 4 3 6 5 4 7 6 5 8 5 4 • Spatial lag = sum of spatiallyweighted values of neighboring cells 4 9 6 Lag for cell 2 = 1/3(7) + 1/3(5) +1/3(4) = 5. 3 3 Sample Region Ids top left and Values in centre

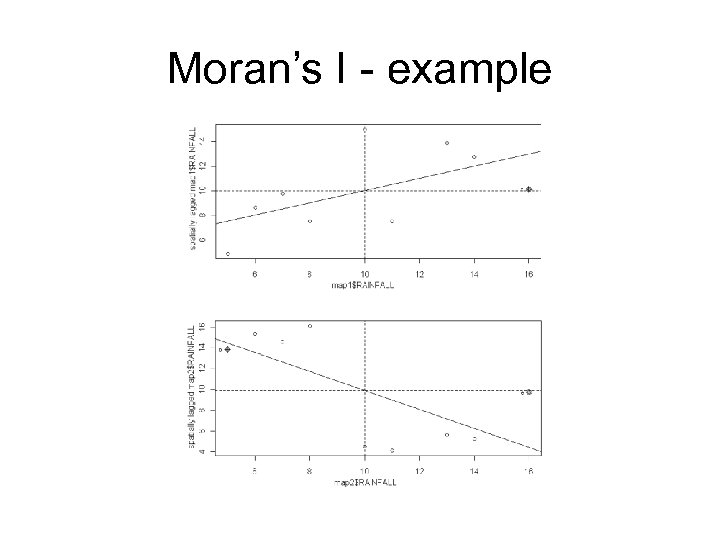
Spatial Lag • Map 1 and Map 2 represent a set of rainfall readings for regions labelled A to I. For both maps the mean is 10, and the standard deviation is 3. 8. • Lag for E in Map 1=(6+7+13+14)/4=10 • Lag for E in Map 2=(7+8+6+5)/4 =6. 5 • In Map 1 the lag=E, in Map 2 lag<E, hence E is more like its neighbours in Map 1 than in Map 2 (Rooks case).
Spatial autocorrelation Negative Dispersed Spatial Independence Spatial Clustering Positive

Moran’s I • Global Moran’s I • What is the extent of clustering in the total area? • Is this clustering significantly different from a random spatial distribution? • Local Moran’s I • Do local clusters (high-high or low-low) or local spatial outliers (high-low or low-high) exist? • Are these local clusters and spatial outliers statistically significant? • Local Moran is a special case of Local indicators of spatial association (LISA)

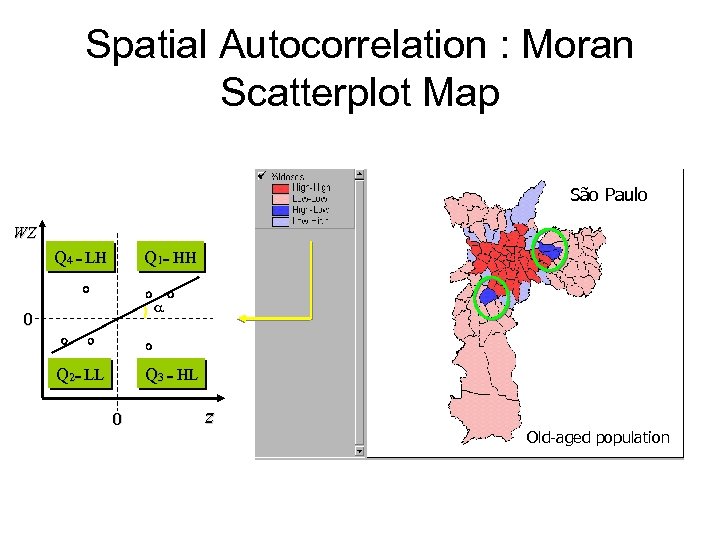
Moran Scatter Plot Scatter Diagram between X and Lag-X, the “spatial lag” of X formed by averaging all the values of X for the neighboring polygons Identifies which type of spatial autocorrelation exists. Low/High negative SA Low/Low positive SA High/High positive SA High/Low negative SA Briggs Henan University 2010 36

Moran’s I index

Unique features of spatial data Statistics • General Statistics assumes the samples are independently generated, which is may not the case with spatial dependent data, where: – Like things tend to cluster together. – Change tends to be gradual over space.
Moran’s I - example
Spatial Autocorrelation : Moran Scatterplot Map São Paulo WZ Q 4 = LH Q 1= HH a 0 Q 2= LL Q 3 = HL 0 z Old-aged population
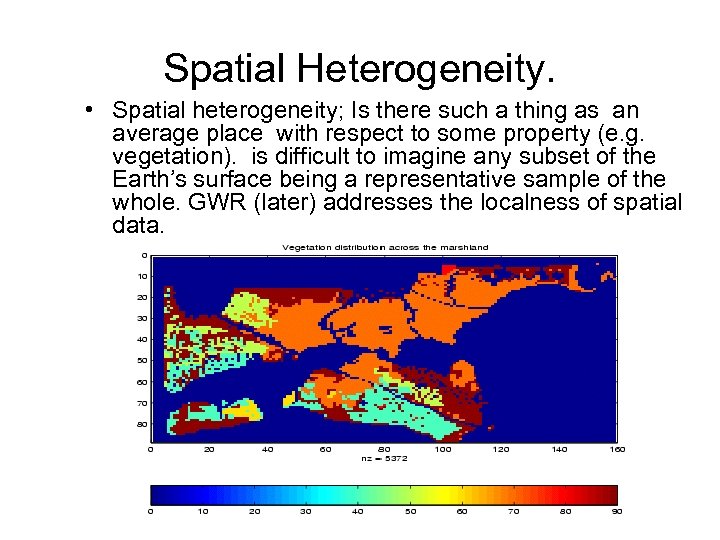
Spatial Heterogeneity. • Spatial heterogeneity; Is there such a thing as an average place with respect to some property (e. g. vegetation). is difficult to imagine any subset of the Earth’s surface being a representative sample of the whole. GWR (later) addresses the localness of spatial data.

Moran’s I: A measure of spatial autocorrelation • Given sampled over n locations. Moran I is defined as Where and W is a normalized contiguity matrix. Fig. 7. 5, pp. 190

How to decide the weight wij ? The weight indicates the spatial interaction between entities. 1) Binary wij, also called absolute adjacency. Covers the general case answering the question is a value in a region similar or different to its neighbours. wij = 1 if two geographic entities are adjacent; otherwise, wij = 0. Choice of adjacency definition queens(8) or rooks(4).

How to decide the weight wij ? The weight indicates the spatial interaction between entities. 2) The distance between geographic entities. Often the inverse distance is used, further objects get less weight, near object get more weight e. g. centre of epidemic. wij = f(dist(i, j)), dist(i, j) is the distance between i and j. 3) The length of common boundary for area entities. Policing borders, smaller borders less weight. wij = f(leng(i, j)), leng(i, j) is the length of common boundary between i and j.

How to decide the weight wij ? 1 The choice of weights should ultimately be driven by a rationale for including those areas as neighbors that have a spatial effect on a given location. This rationale can be derived from theory or be the result of using ESDA to experiment with different weights and connectivity orders. Since weights matrices are used to create spatial lags that average neighboring values, the choice of a weights matrix will determine which neighboring values will be averaged. For instance, since rook weights will usually have fewer neighbors than queen weights, on average, each neighboring observation has more influence.

How to decide the weight wij ? 1 The question of which weights to choose is more pertinent in the context of modeling than ESDA since modeling is based on substantive notions of spatial effects while ESDA prioritizes the rejection of spatial randomness. Therefore, if there are no substantive reasons to guide the choice of weights in ESDA, using a weights file with as few neighbors as possible (such as rook) makes sense. Especially with irregular areal units (as opposed to grids), the difference between rook and queen weights is often minimal. However, it is advisable to test how sensitive your results are to your weights specifications by comparing multiple weights matrices.

Spatial Outlier Detection • Global outliers are observations which appear inconsistent with the remainder of that data set. • Global outliers deviate so much from other observations that it may be possible that they were generated by a different mechanism. • Spatial outliers are observations that appear inconsistent with their neighbours.

Spatial Outlier Detection • Detecting spatial outliers has important applications in transportation, ecology, public safety, public health, climatology and location based services. • Geographic objects have a spatial (location, shape, metric & topological properties) & non-spatial component (house owner, sensor id. , soil type).

Spatial Outlier Detection • Spatial neighbourhoods may be defined using spatial attributes & spatial relations. • Comparisons between spatially referenced objects can be based on non-spatial attributes. • A spatial outlier is a spatially referenced object whose non-spatial attribute values differ from those of other spatially referenced objects in its spatial neighbourhood.
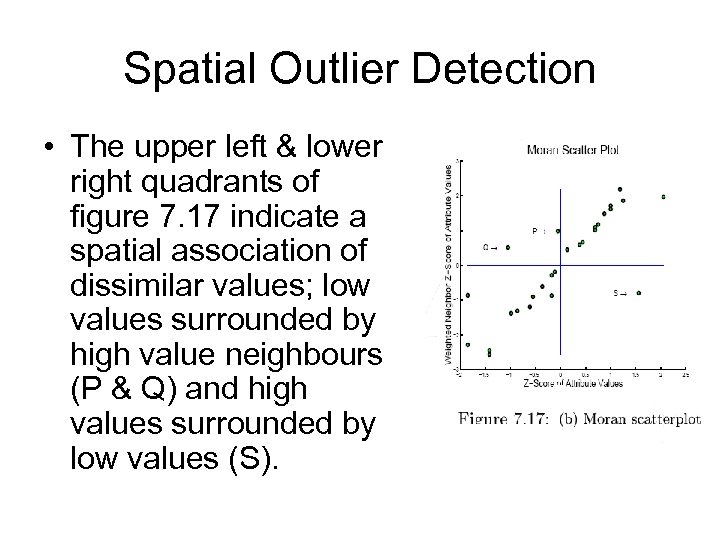
Spatial Outlier Detection • The upper left & lower right quadrants of figure 7. 17 indicate a spatial association of dissimilar values; low values surrounded by high value neighbours (P & Q) and high values surrounded by low values (S).
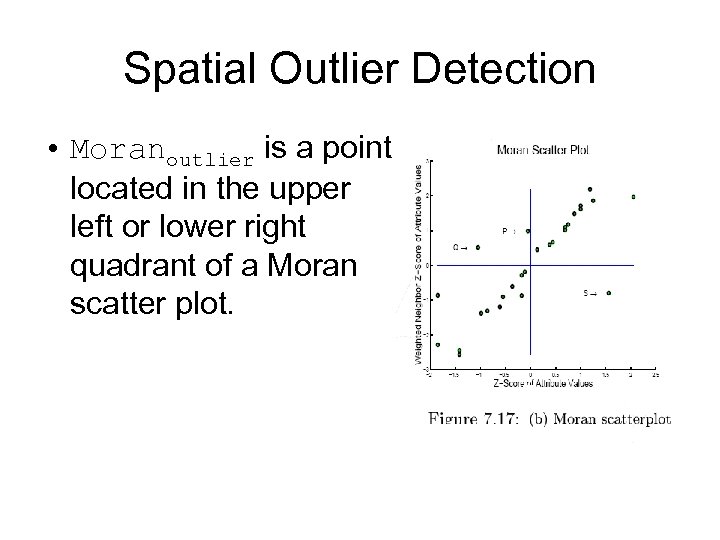
Spatial Outlier Detection • Moranoutlier is a point located in the upper left or lower right quadrant of a Moran scatter plot.
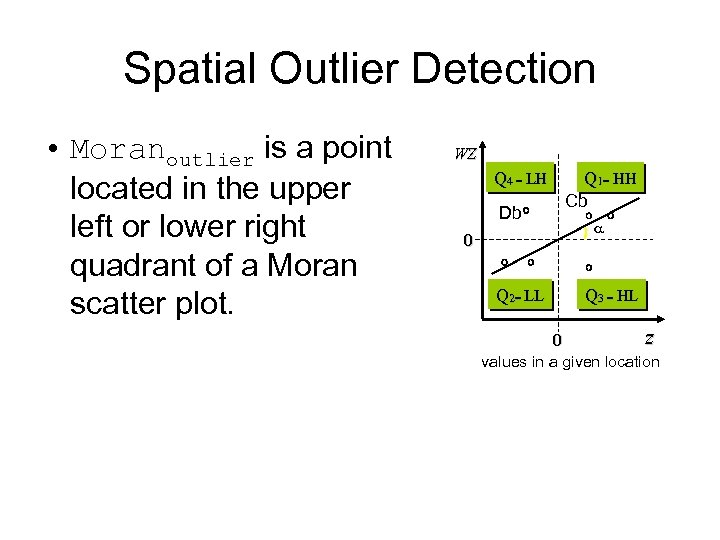
Spatial Outlier Detection • Moranoutlier is a point located in the upper left or lower right quadrant of a Moran scatter plot. WZ Q 4 = LH Db 0 Q 2= LL Q 1= HH Cb a Q 3 = HL z 0 values in a given location

2. Some definitions • Spatial non-stationarity: the same stimulus provokes a different response in different parts of the study region • Global models: statements about processes which are assumed to be stationary and as such are location independent

Some definitions • Local models: spatial decompositions of global models, the results of local models are location dependent – a characteristic we usually anticipate from geographic (spatial) data

Regression • Regression establishes relationship among a dependent variable and a set of independent variable(s) • A typical linear regression model looks like: • yi= 0 + 1 x 1 i+ 2 x 2 i+……+ nxni+ i • With yi the dependent variable, xji (j from 1 to n) the set of independent variables, and i the residual, all at location i
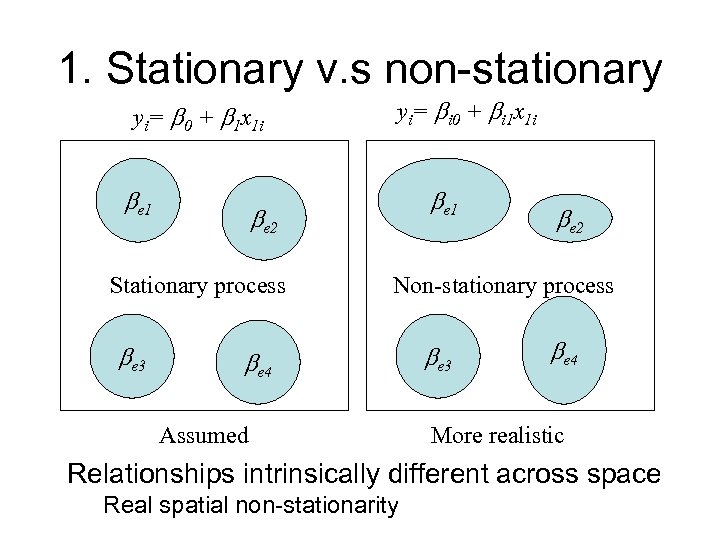
1. Stationary v. s non-stationary yi= 0 + 1 x 1 i e 1 e 2 Stationary process e 3 yi= i 0 + i 1 x 1 i e 2 Non-stationary process e 4 Assumed e 3 e 4 More realistic Relationships intrinsically different across space Real spatial non-stationarity
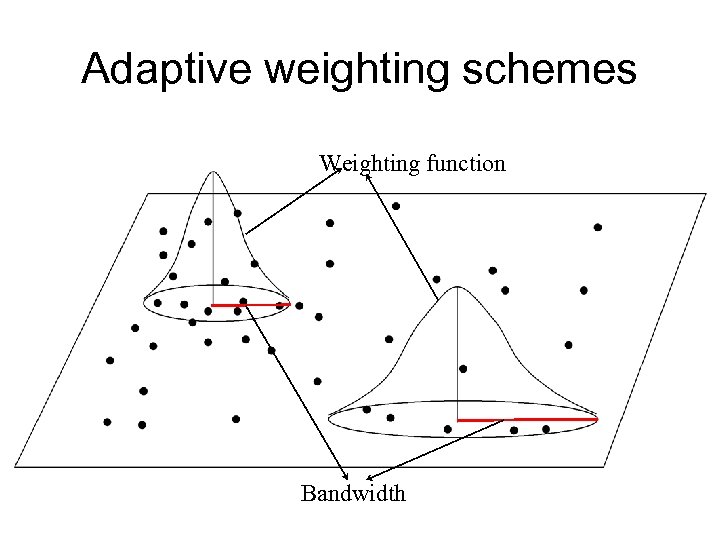
Adaptive weighting schemes Weighting function Bandwidth
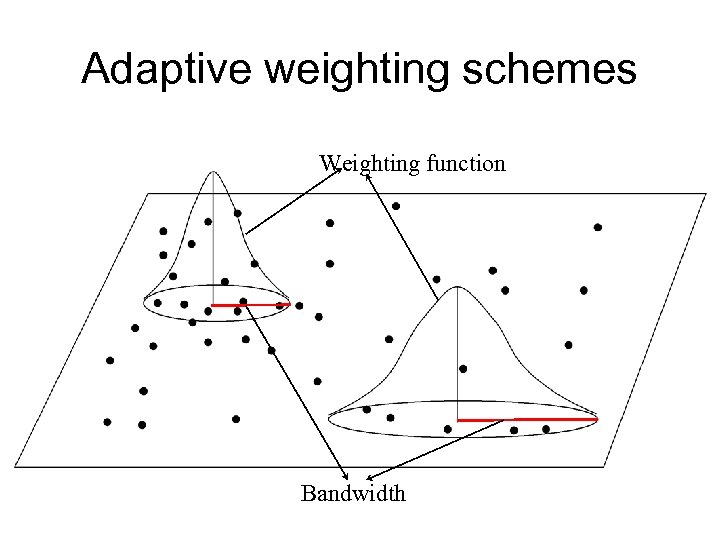
Adaptive weighting schemes Weighting function Bandwidth

Geographically Weighted Regress ion (GWR)
dbdb3df3b854774498f82f69bae123d9.ppt