7cf03dcf8c2b01c90135050ce076fa4c.ppt
- Количество слайдов: 44

Sparsity-based sub-wavelength imaging and super-resolution in time and frequency Yoav Shechtman Physics Department, Technion, Haifa 32000, Israel Alex Szameit, Snir Gazit, Pavel Sidorenko, Elad Bullkich, Eli Osherovic, Michael Zibulevsky, Irad Yavneh, Yonina Eldar , Oren Cohen, Moti Segev FRISNO 2011 Nonlinear Optics Laboratory

Sub-wavelength images in the microscope Nonlinear Optics Laboratory

Optical cut-off for high spatial frequencies field propagation (z = 0 → z > 0) propagating waves evanescent waves Nonlinear Optics Laboratory

Hardware solutions for sub-wavelength imaging • Scanning near-field optical microscope • Methods using florescent particles • Structured Illumination • Negative-index / metamaterials structures: superlens, hyperlens • Hot-spot methods: nano-hole array, super-oscillations Require scanning, averaging over multiple experiments Is it possible to have real-time, single exposure subwavelength imaging using a ‘regular’ microscope? Nonlinear Optics Laboratory

Analytic Continuation • The 2 D Fourier transform of a spatially bounded function is an analytic function. • Problem: Existing analytic continuation methods are not very robust: • sampling theorem based extrapolations yield a highly ill posed matrix. • Iterative methods (Gerchberg - Papoulis) are sensitive to noise Nonlinear Optics Laboratory

Common wisdom “All methods for extrapolating bandwidth beyond the diffraction limit are known to be extremely sensitive to both • noise in the measured data and • the accuracy of the assumed a priori knowledge. ” “It is generally agreed that the Rayleigh diffraction limit represents a practical frontier that cannot be overcome with a conventional imaging system. ” J. W. Goodman, Introduction to Fourier Optics, 2005 Nonlinear Optics Laboratory
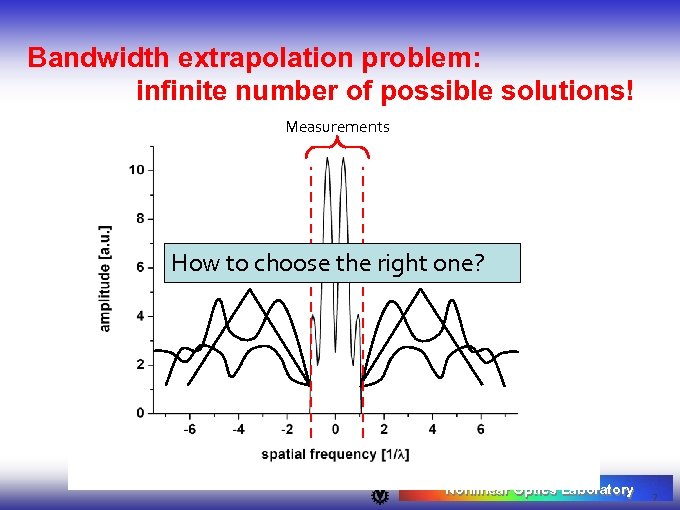
Bandwidth extrapolation problem: infinite number of possible solutions! Measurements How to choose the right one? Nonlinear Optics Laboratory 7

Problem: non-invertible filter FT(signal) Measurements Filtered Fourier transform (non-invertible) Fourier transform (invertible) signal buried in the noise (exponentially small evanescent waves) Nonlinear Optics Laboratory 8

Under-determined system of equations • Under-determined system of equations: more variables than equations • Infinite number of solutions (x) • Choose the one that “makes the most sense” We choose the solution with maximum sparsity – • Based on what? the one with the fewest nonzero elements. Based on the knowledge that the object is sparse in a known basis. Nonlinear Optics Laboratory 9

Why sparsity? • General: Many objects are sparse in some (general) basis. • Powerful: • Robust to noise. Without noise, in a sparse enough case the sparsest solution is unique • Sparsity is used successfully for image denoising, deconvolution, compression, enhancement of MR images and more. However – has never been used for sub-λ imaging, or temporal bandwidth extrapolation. • Attainable: Efficient algorithms exist for estimating Nonlinear Optics Laboratory 10 the sparsest solution.

Sparsity – a general feature of information Sparsity in real space image biological species: Real-space sparsity ~ 2 - 5% Sparsity in another basis Electronic chips: Sparsity in gradient basis ~ few % Nonlinear Optics Laboratory

How to do it: for example - Basis Pursuit Solve the (convex) optimization problem: • x : unknown image • y: measured image • A: Low-pass filter + sparsity basis • ε: Noise parameter • The requirement on the l 1 norm is to promote sparsity. • Find the sparsest x that is consistent with the measurements. [S. S. Chen et al. , SIAM Journal on Scientific Computing, 20, 33 (1998)] Nonlinear Optics Laboratory 12
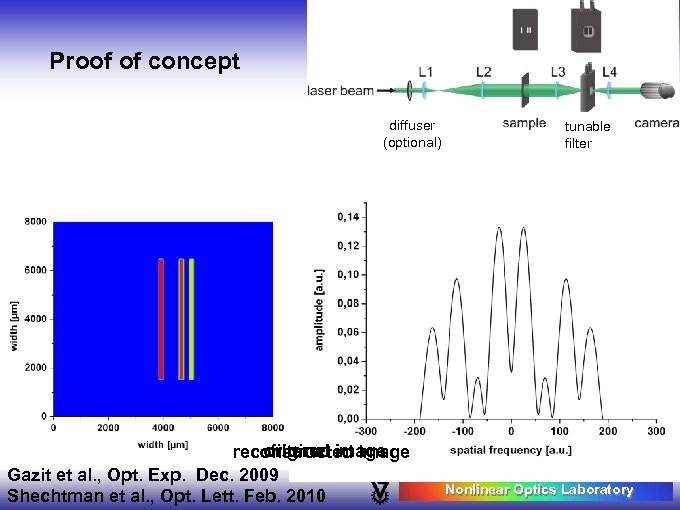
Proof of concept diffuser (optional) original image filtered reconstructed image Gazit et al. , Opt. Exp. Dec. 2009 Shechtman et al. , Opt. Lett. Feb. 2010 tunable filter Nonlinear Optics Laboratory
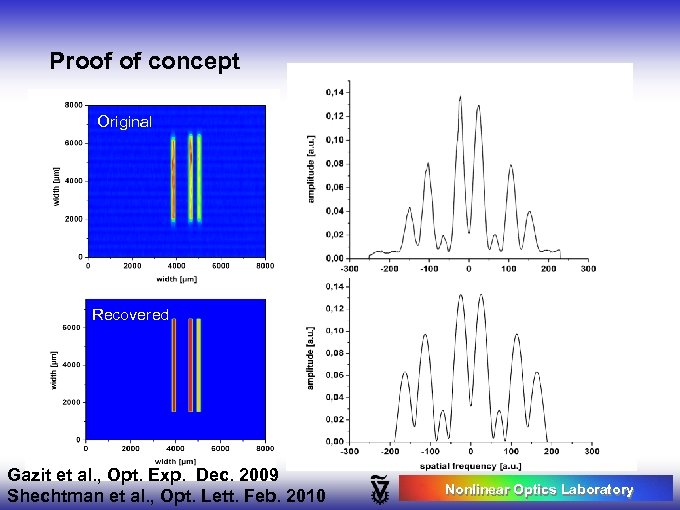
Proof of concept Original Recovered Gazit et al. , Opt. Exp. Dec. 2009 Shechtman et al. , Opt. Lett. Feb. 2010 Nonlinear Optics Laboratory

True sub-l experiments – 1 D @ l = 532 nm SEM image Chromium Glass Width: 150 nm Length: 20 µm Spacing: 150 nm (left/right pair) 300 nm (center) ~ diffraction limit Fabrication: Kley – group University of Jena kley@iap. uni-jena. de Nonlinear Optics Laboratory

Best possible microscope image (NA ≈ 1) Nonlinear Optics Laboratory
Microscope image far-field Nonlinear Optics Laboratory
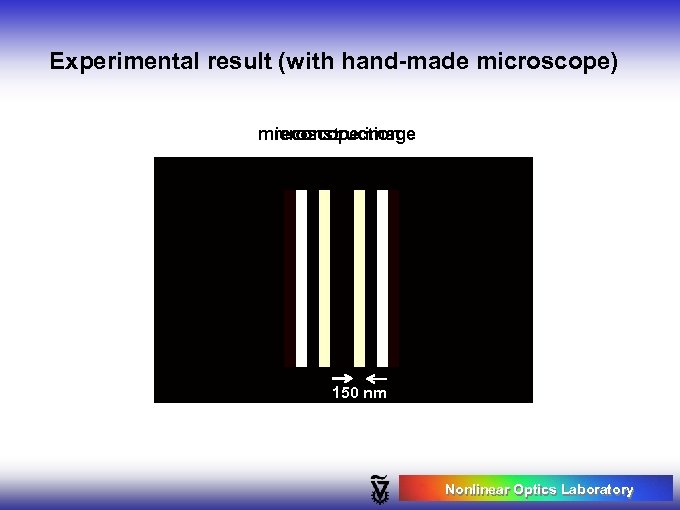
Experimental result (with hand-made microscope) reconstruction microscope image 150 nm Nonlinear Optics Laboratory
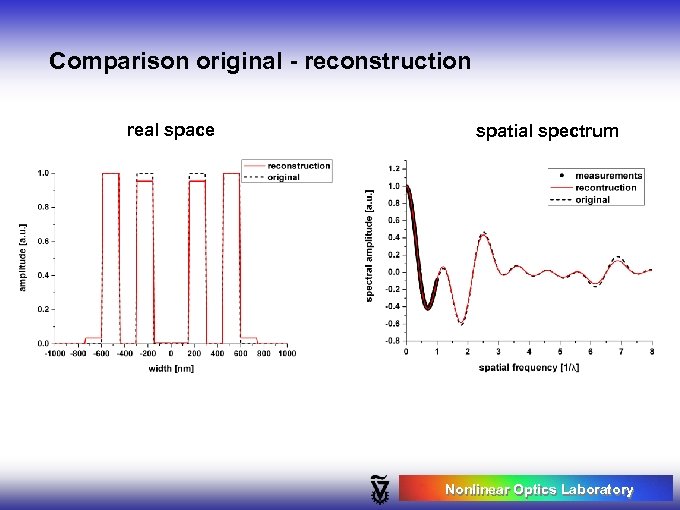
Comparison original - reconstruction real space spatial spectrum Nonlinear Optics Laboratory

True sub-l experiments – 2 D @ l = 532 nm 100 nm Nonlinear Optics Laboratory

Best possible microscope image (NA ≈ 1) Nonlinear Optics Laboratory
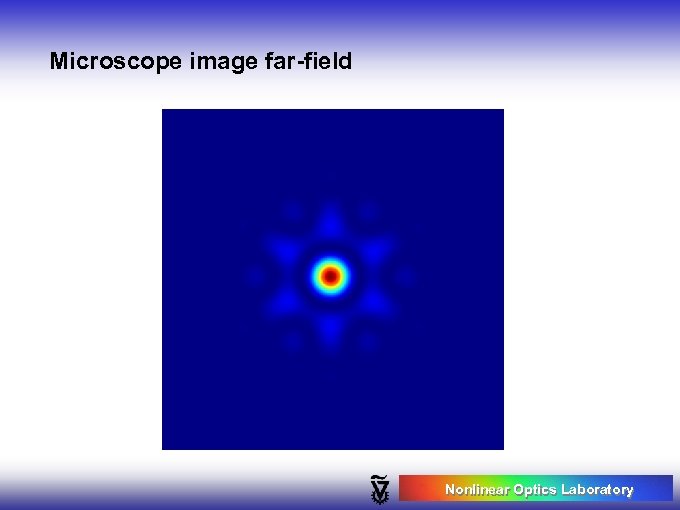
Microscope image far-field Nonlinear Optics Laboratory

Loss of power in the far-field more than 90% of the intensity is lost Nonlinear Optics Laboratory
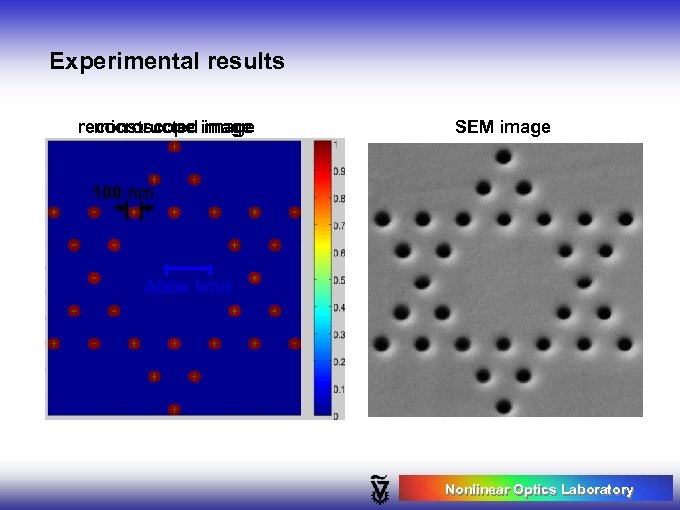
Experimental results microscope image reconstructed image SEM image 100 nm Abbe limit Nonlinear Optics Laboratory

Sub-l imaging from far-field intensity measurements Can we do sub-wavelength reconstruction based on intensity measurements only? Without measuring phase at all? Yes, indeed. The knowledge of sparsity is powerful. First: Fourier phase recovery using iterative algorithm* – given the blurred image intensity and Fourier intensity. Second: sparsity-based reconstruction using recovered phase. or, better, combine the two! * J. R. Fienup, Appl. Opt. 21 (1982) Nonlinear Optics Laboratory
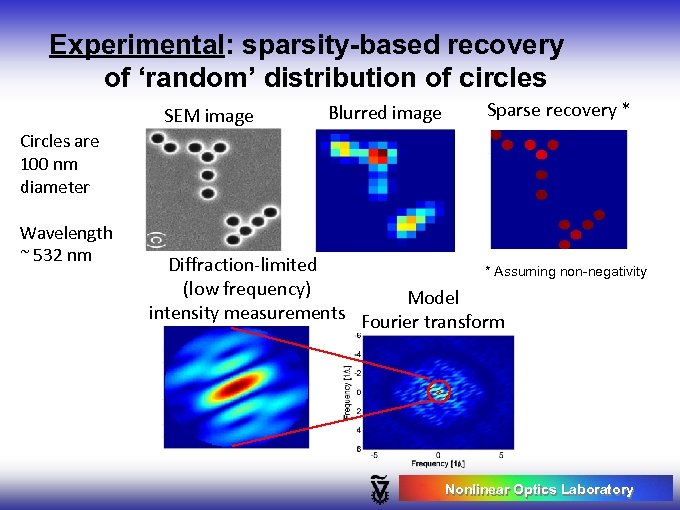
Experimental: sparsity-based recovery of ‘random’ distribution of circles SEM image Blurred image Sparse recovery * Circles are 100 nm diameter Wavelength ~ 532 nm Diffraction-limited * Assuming non-negativity (low frequency) Model intensity measurements Fourier transform Nonlinear Optics Laboratory
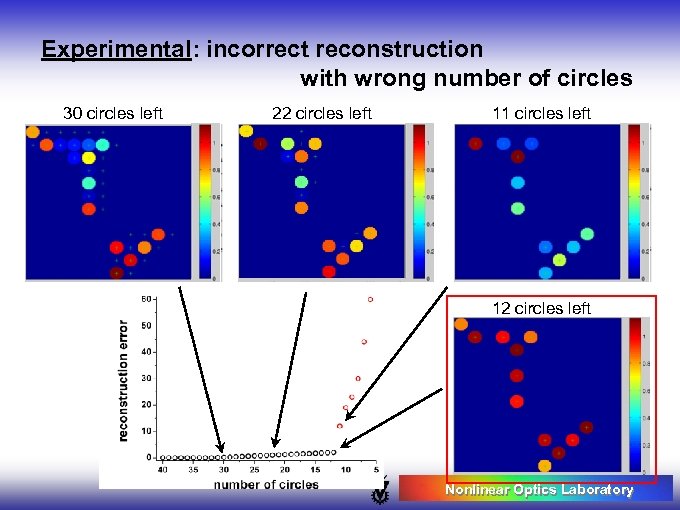
Experimental: incorrect reconstruction with wrong number of circles 30 circles left 22 circles left 11 circles left 12 circles left Nonlinear Optics Laboratory
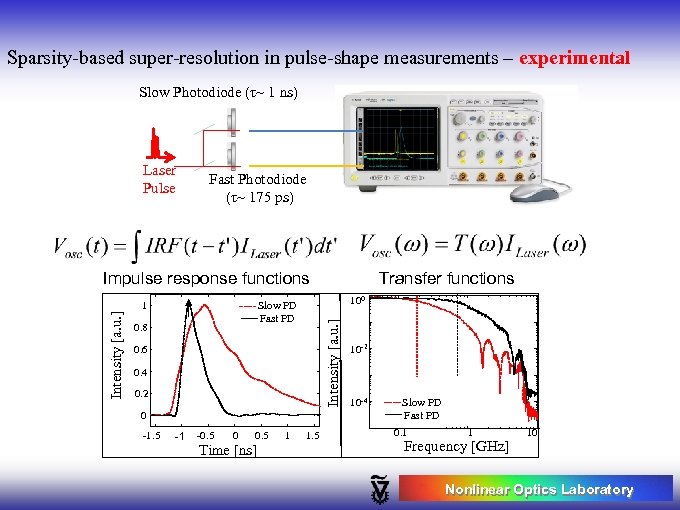
Sparsity-based super-resolution in pulse-shape measurements – experimental Slow Photodiode (τ~ 1 ns) Laser Pulse Fast Photodiode (τ~ 175 ps) Impulse response functions Transfer functions (b) 1 Slow PD Fast PD 0. 8 0. 6 0. 4 0. 2 100 Intensity [a. u. ] (c) 10 -2 Slow PD Fast PD 10 -4 0 -1. 5 -1 -0. 5 0 0. 5 Time [ns] 1 1. 5 0. 1 1 Frequency [GHz] 10 Nonlinear Optics Laboratory
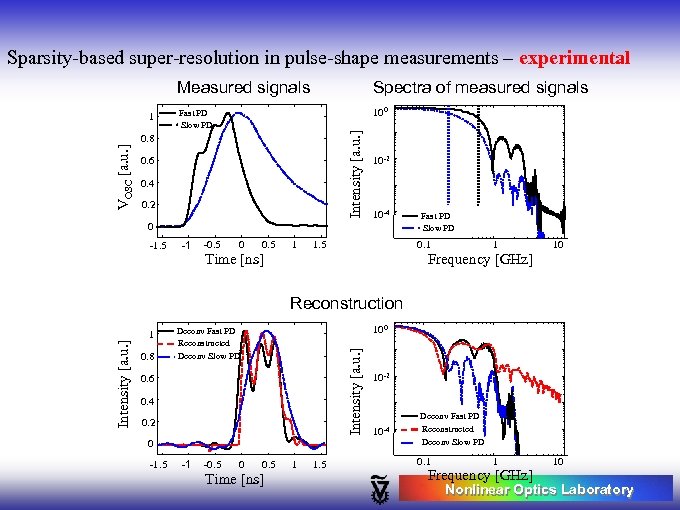
Sparsity-based super-resolution in pulse-shape measurements – experimental Measured signals Fast PD Slow PD 100 Intensity [a. u. ] 1 VOSC [a. u. ] Spectra of measured signals 0. 8 0. 6 0. 4 0. 2 0 -1. 5 -1 -0. 5 0 0. 5 1 (c) 10 -2 10 -4 Fast PD Slow PD 1. 5 0. 1 1 Frequency [GHz] Time [ns] 10 Deconv Fast PD Reconstructed Deconv Slow PD 1 0. 8 0. 6 0. 4 0. 2 0 -1. 5 -1 -0. 5 0 100 Intensity [a. u. ] Reconstruction 0. 5 Time [ns] 1 1. 5 (c) 10 -2 Deconv Fast PD Reconstructed Deconv Slow PD 10 -4 0. 1 1 Frequency [GHz] 10 Nonlinear Optics Laboratory

Sparsity-based super-resolution FTIR spectroscopy -x 0 x Light Source Power (W) Fixed Mirror BS Moving Mirror Power (W) X (cm) λ (nm) Detector Because the interferogram cannot be collected from x = - to + , it is always truncated, hence some error arises in the resulting spectrum: the spectral line is broadened + side-lobes are added Resolution of a F-T spectrometer: Δλ = 1 / (path difference = 4 x) Nonlinear Optics Laboratory
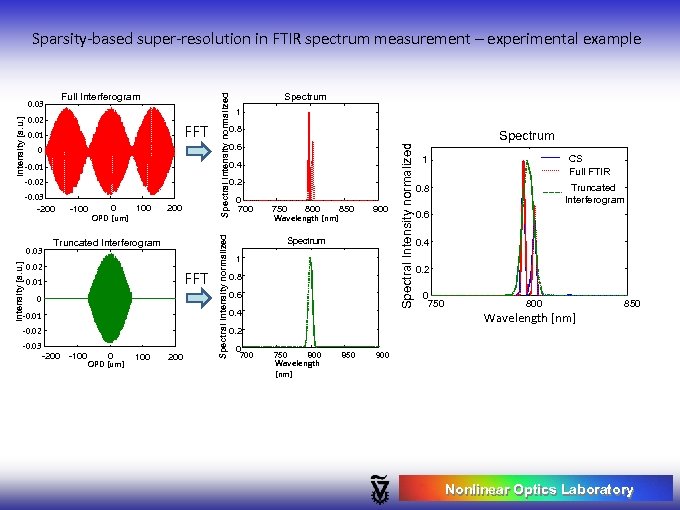
FFT 0. 01 0. 6 0 0. 4 -0. 01 -0. 02 0. 2 -0. 03 -200 Intensity [a. u. ] 0. 03 -100 0 100 OPD [um] 200 Truncated Interferogram 0. 02 FFT 0. 01 0 -0. 01 -0. 02 -0. 03 1 0. 8 -200 -100 0 OPD [um] 100 200 Spectral Intensity normalized Intensity [a. u. ] 0. 02 Spectrum 0 700 750 800 850 Wavelength [nm] 900 Spectrum 1 0. 8 0. 6 0. 4 Spectral Intensity normalized Full Interferogram 0. 03 Spectral Intensity normalized Sparsity-based super-resolution in FTIR spectrum measurement – experimental example Spectrum CS Full FTIR 1 Truncated Interferogram 0. 8 0. 6 0. 4 0. 2 0 750 800 850 Wavelength [nm] 0. 2 0 700 750 800 Wavelength [nm] 850 900 Nonlinear Optics Laboratory

Conclusions • method for recovering sub-l information from the optical far-field of images • requires no additional hardware • works in real time and with ultrashort pulses • applicable to all microscopes (optical and non-optical) • reconstruction also with incoherent / partially coherent light • Ideas are universal: can be used to recover • shapes of ultrashort pulses in time • spectral features quantum info! Nonlinear Optics Laboratory

Many thanks for your attention! Nonlinear Optics Laboratory

Nonlinear Optics Laboratory
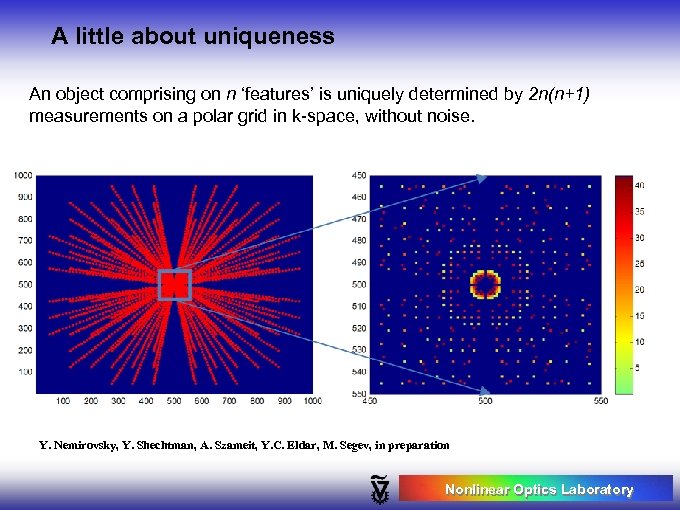
A little about uniqueness An object comprising on n ‘features’ is uniquely determined by 2 n(n+1) measurements on a polar grid in k-space, without noise. Y. Nemirovsky, Y. Shechtman, A. Szameit, Y. C. Eldar, M. Segev, in preparation Nonlinear Optics Laboratory

Comparison of approaches Original CS approach Our CS-related approach • measurement in uncorrelated basis (commonly Fourier basis) • measurement in far-field (= Fourier basis) OR blurred near field or in between • sampling (randomly) over the entire measurement basis with low resolution • sampling in a small part of the measurement basis (kx < k) with high resolution • reduction of required samples to retrieve the function • obtain maximal info on the frequency region where we do NOT measure We do NOT do CS. We do NOT use CS “rules”. Why does it work for us? Nonlinear Optics Laboratory

Unique sparse solution sparse triangle inequality: if every S 1+S 2 columns of W are linearly independant if , then there is a unique sparse solution matrix coherence Nonlinear Optics Laboratory
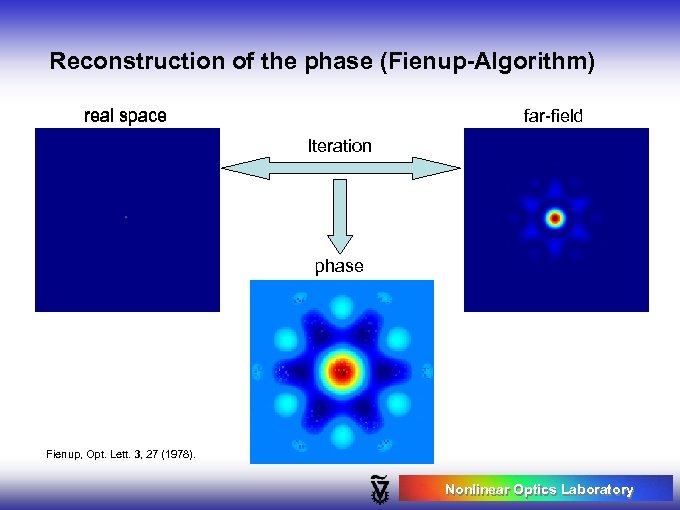
Reconstruction of the phase (Fienup-Algorithm) real space far-field Iteration phase Fienup, Opt. Lett. 3, 27 (1978). Nonlinear Optics Laboratory
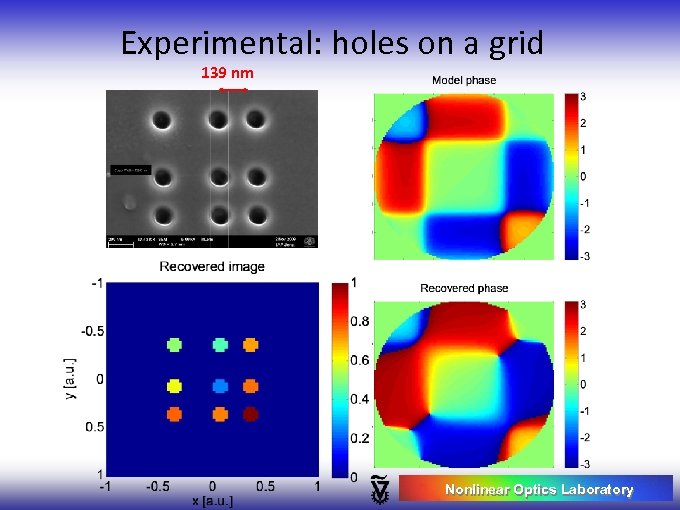
Experimental: holes on a grid 139 nm Nonlinear Optics Laboratory

* Consider a function spikes: that can be written as a superposition of If it is comprises of spikes, and N is a prime number, then can be uniquely defined by any of its Fourier measurements, defined as: Specifically, the low pass Fourier coefficients will do. * Candes, E. J. ; Romberg, J. ; Tao, T. ; , "Robust uncertainty principles: exact signal reconstruction from highly incomplete frequency information, " Information Theory, IEEE Transactions on , vol. 52, no. 2, pp. 489 - 509, Feb. 2006 Nonlinear Optics Laboratory
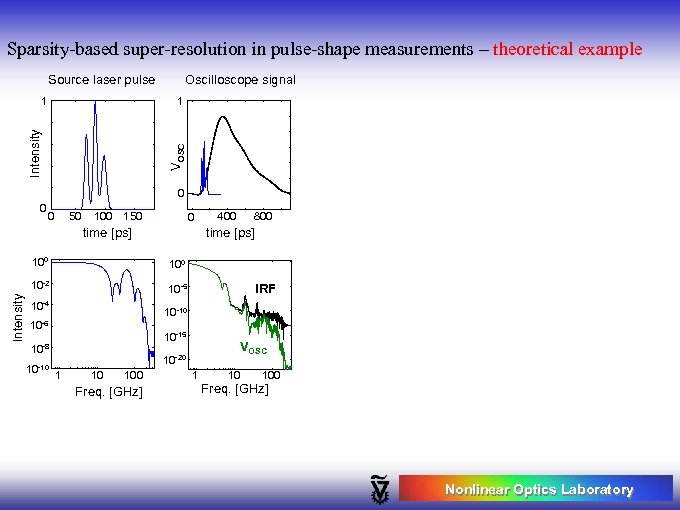
Sparsity-based super-resolution in pulse-shape measurements – theoretical example Source laser pulse Oscilloscope signal 1 VOSC Intensity 1 0 0 0 50 100 150 0 time [ps] 800 time [ps] 100 Intensity 400 10 -2 10 -5 10 -4 10 -10 10 -6 10 -15 10 -8 10 -10 IRF VOSC 10 -20 1 10 100 Freq. [GHz] Nonlinear Optics Laboratory
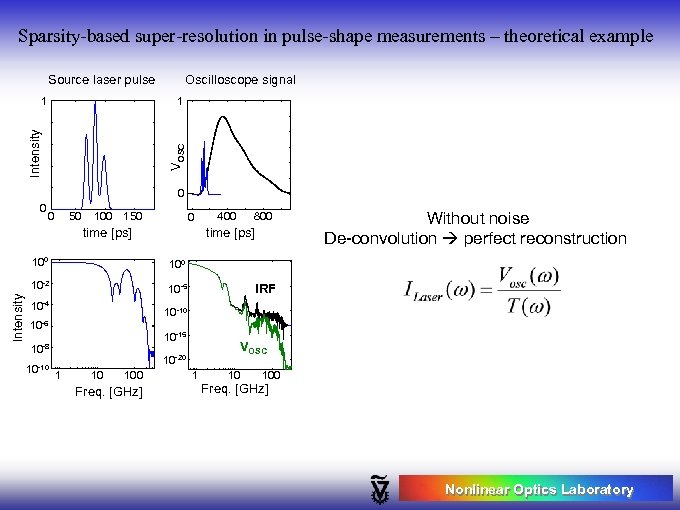
Sparsity-based super-resolution in pulse-shape measurements – theoretical example Source laser pulse Oscilloscope signal 1 VOSC Intensity 1 0 0 0 50 100 150 0 time [ps] 800 time [ps] 100 Intensity 400 10 -2 10 -5 Without noise De-convolution perfect reconstruction 10 -4 10 -10 10 -6 10 -15 10 -8 10 -10 IRF VOSC 10 -20 1 10 100 Freq. [GHz] Nonlinear Optics Laboratory
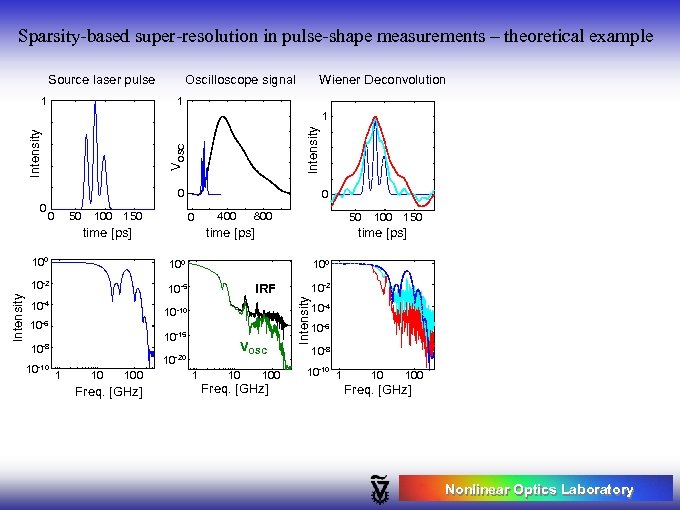
Sparsity-based super-resolution in pulse-shape measurements – theoretical example Source laser pulse Oscilloscope signal Wiener Deconvolution VOSC Intensity 1 1 0 0 0 50 100 150 0 0 time [ps] 800 50 10 -2 10 -5 IRF 10 -15 10 -8 10 -10 10 -6 VOSC 10 -20 1 10 100 Freq. [GHz] 100 150 time [ps] 1 10 100 Freq. [GHz] Intensity 400 time [ps] 100 10 -4 1 10 -2 10 -4 10 -6 10 -8 10 -10 100 Freq. [GHz] Nonlinear Optics Laboratory
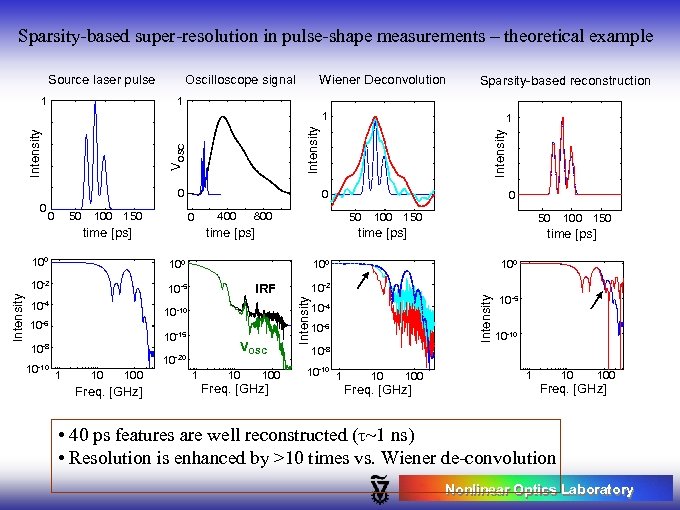
Sparsity-based super-resolution in pulse-shape measurements – theoretical example Source laser pulse Oscilloscope signal Wiener Deconvolution 0 50 100 150 0 0 time [ps] 800 10 -5 10 -4 10 -10 IRF 10 -15 10 -8 VOSC 10 -20 1 10 100 Freq. [GHz] 50 1 10 100 Freq. [GHz] 100 150 time [ps] 100 10 -10 10 -6 100 150 time [ps] 100 10 -2 0 50 Intensity 400 time [ps] 100 1 10 -2 Intensity 0 1 Intensity VOSC Intensity 1 1 0 Sparsity-based reconstruction 10 -4 10 -6 10 -5 10 -10 10 -8 10 -10 100 Freq. [GHz] • 40 ps features are well reconstructed (τ~1 ns) • Resolution is enhanced by >10 times vs. Wiener de-convolution Nonlinear Optics Laboratory
7cf03dcf8c2b01c90135050ce076fa4c.ppt