Space Geometry Skew line
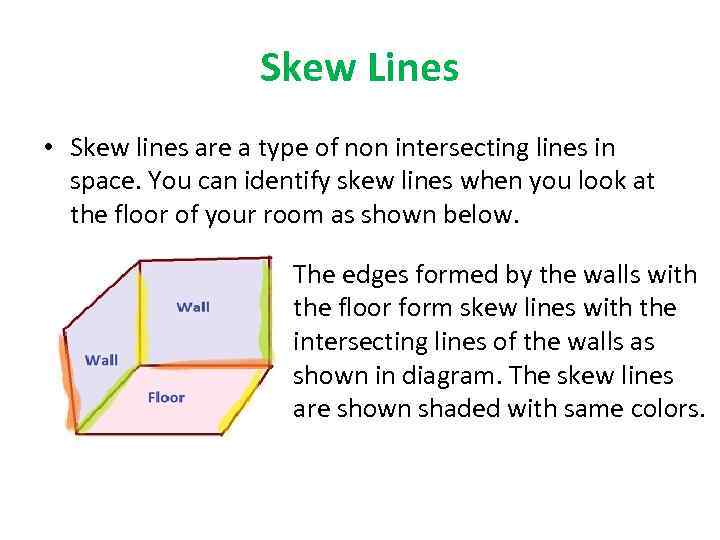Skew Lines • Skew lines are a type of non intersecting lines in space. You can identify skew lines when you look at the floor of your room as shown below. The edges formed by the walls with the floor form skew lines with the intersecting lines of the walls as shown in diagram. The skew lines are shown shaded with same colors.
Skew Lines Definition • Non coplanar lines in space that do not intersect are called skew lines. • Segments and rays contained in skew lines are also skew. Let us identify the skew edges of the cube ABCDEFGH. 1. Edges AB and CD. 2. Edges AB and GH. 3. Edges BC and AF. 3. Edges BC and GH. 5. Edges CH and AF. 6. Edges CH and BE. 7. Edges AH and BE. 8. Edges AH and CD. 9. Edges DE and AF. 10. Edges DE and GH. 11. Edges EF and GH. 12. Edged EF and CD. 13. Edges FG and BE 14. Edges FG and CD. 15. Edges GD and BE. 16. Edges GD and AF. NOTE: You may also note any diagonal of a face is skew to the edges of the opposite face, like AC is skew to GD. The angle between two lines the angle between two coplanar lines drawn parallel to the two lines.
Skew line in life
Skew Lines in Real Life • 1. A road over a bridge crossing a railway track below. 2. The upright tree on one bank of a river, to the straight opposite Bank. 3. The edge of your cupboard door and the spread on your bed. 4. The Balcony railing is skew to the stick placed with its top touching the side wall. You can find many such examples inside and outside your house or if you look around your class room.
Distance between Skew Lines • The shortest distance between two skew lines is the length of the line segment perpendicular to both the lines. It is possible to identify two parallel planes each containing one of the skew lines. In the example of cube, we identified AB and CD as two skew line segments. The plane ABEF containing the line AB and the plane CDGH containing the line CD are parallel panes. Hence the distance between the two skew lines AB and CD = distance between the parallel planes ABEF and CDGH. = distance BC
Thus we can identify a parallel plane ax + by + cz + d = 0 containing one of the skew lines and a point P(x 0, y 0, z 0) lying on the other skew line and use the formula to find the perpendicular distance of the plane from the point, which would be the distance between the two skew lines.
Solved Example Question: Find the distance between the skew lines L 1 and L 2 whose parametric equations are given as follows: L 1 : x = 1 + 2 t, y = 3 t and z = 2 - t. L 2 : x = -1 + s, y = 4 + s, z = 1 + 3 s. • Step 1: Finding equation of a plane containing the line L 2. Let P 1 and P 2 be the two parallel planes containing L 1 and L 2. The common normal vector of these planes 'n' must be orthogonal to both v 1 = <2, 3, -1> (direction of L 1) and v 2 = <1, 1, 3> (direction of L 2). The normal vector n = v 1 x v 2 = = i(9 + 1) -j(6 + 1) +k(2 - 3) = 10 i -7 j - k. • If we put s =0, in the equation of L 2, we get a point on L 2 as (-1, 4, 1). Thus the equation of the plane P 2 is, a(x - x 0) + B(y - y 0) + c(z -z 0) = 10 10(x + 1) -7(y - 4) -(z -1) = 0 10 x - 7 y - z + 39 = 0 Equation of plane P 2.
• Step 2: Finding a point on line L 1. If we let t = 0 in the equation of L 1, we get the point on L 1 as (1, 0, 2). • Step 3: Use distance formula to find the distance between the skew lines Now we need to find the distance between the point (1, 0, 2) and the plane P 2, using the formula • The distance between the skew lines L 1 and L 2 ≈ 3. 84 units.