Современная теория алгоритмов Лекция 2 -2

Современная теория алгоритмов Лекция № 2 -2

Современная теория алгоритмов • Начальной точкой отсчета современной теории алгоритмов можно считать теорему о неполноте символических логик, доказанную немецким математиком Куртом Геделем в 1931 г. • В этой работе было показано, что некоторые математические проблемы не могут быть решены алгоритмами определенного класса. • Общность результата Геделя связана с вопросом о том, совпадает ли использованный им класс алгоритмов с классом всех алгоритмов в интуитивном понимании этого термина. • Эта работа дала толчок к поиску и анализу различных формализаций понятия «алгоритм» .

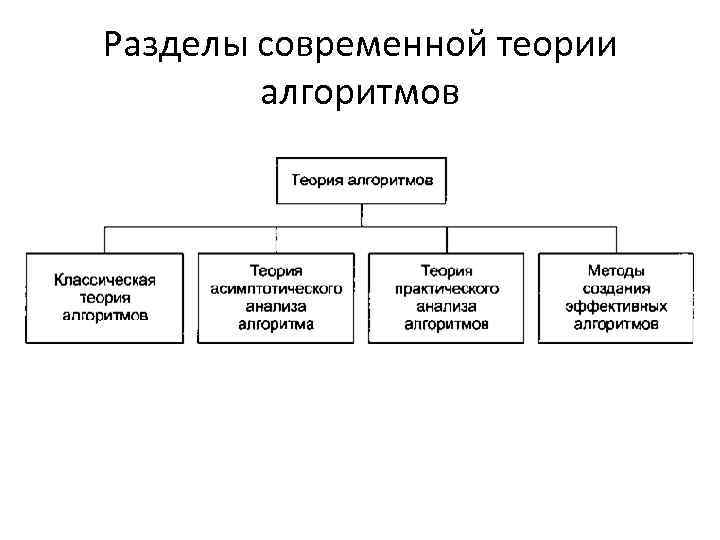Разделы современной теории алгоритмов

Классическая теория алгоритмов • формулировка задач в терминах формальных языков; • понятие задачи разрешения; описание сложных классов задач; • введение новых моделей вычислений — алгебраического дерева вычислений, машины с произвольным доступом к памяти, схем алгоритмов Янова, стандартных схем программ Котова

Теория асимптотического анализа алгоритмов • понятие сложности и трудоемкости алгоритма; • критерии оценки алгоритмов; • методы получения асимптотических оценок, в частности, для рекурсивных алгоритмов; • асимптотический анализ трудоемкости или времени выполнения; • получение теоретических нижних оценок сложности задач.

Теория практического анализа вычислительных алгоритмов • получение явных функций трудоемкости; • интервальный анализ функций; • практически значимые критерии качества алгоритмов; • методики выбора рациональных алгоритмов.

Методы создания эффективных алгоритмов • множество алгоритмов, среди которых динамическое программирование, метод ветвей и границ, метод декомпозиции, «жадные» алгоритмы, специальные структуры данных.

Современные теории алгоритмов • формализация понятия «алгоритм» и исследование формальных алгоритмических систем; • доказательство алгоритмической неразрешимости задач; • формальное доказательство правильности и эквивалентности алгоритмов; • классификации задач, определение и исследование сложных классов; • доказательство теоретических нижних оценок сложности задач; • получение методов разработки эффективных алгоритмов; • асимптотический анализ сложности итерационных алгоритмов; • исследование и анализ рекурсивных алгоритмов; • получение явных функций трудоемкости алгоритмов; • разработка классификаций алгоритмов; • исследование емкостной (по ресурсу памяти) сложности задач и алгоритмов; • разработка критериев сравнительной оценки ресурсной эффективности алгоритмов и методов их сравнительного анализа.

Обработка данных в виде символьных цепочек • Символьные цепочки представляют собой обыкновенные массивы типа CHAR. • Особенность этого типа данных состоит в том, что символьный массив в подавляющем большинстве случаев является осмысленным текстом, а значит, имеет логическую структуру: разделен на слова, предложения, строки и абзацы. • Поэтому алгоритмы обработки символьных цепочек почти всегда включают в себя поиск специальных символов-разделителей, разделение текста на логические единицы (слова, предложения, строки) и выполнение операций (подсчет, сортировка, поиск и замена) над этими единицами.

Обработка данных в виде одно- и двусвязных списков • Структура данных, в которой объекты расположены в линейном порядке, называется связным списком. • Однако в отличие от массива, в котором этот порядок определяется индексами, порядок в связном списке определяется указателями на объекты

Элемент (узел) связного списка • помимо полей с данными, имеет поле next, в котором содержится указатель на следующий элемент списка. • Если это последний элемент списка, поле next принимает нулевое значение. • Помимо своих элементов, каждый список содержит указатель head на первый элемент списка. • Если этот указатель равен 0, значит, список пуст.

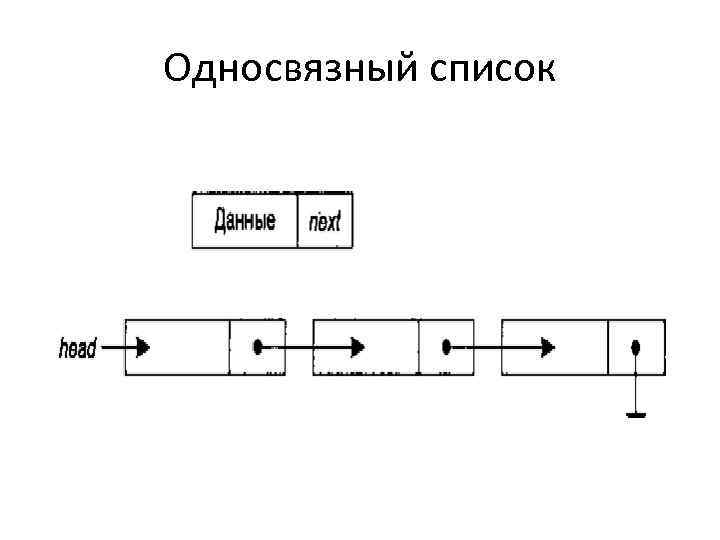Односвязный список

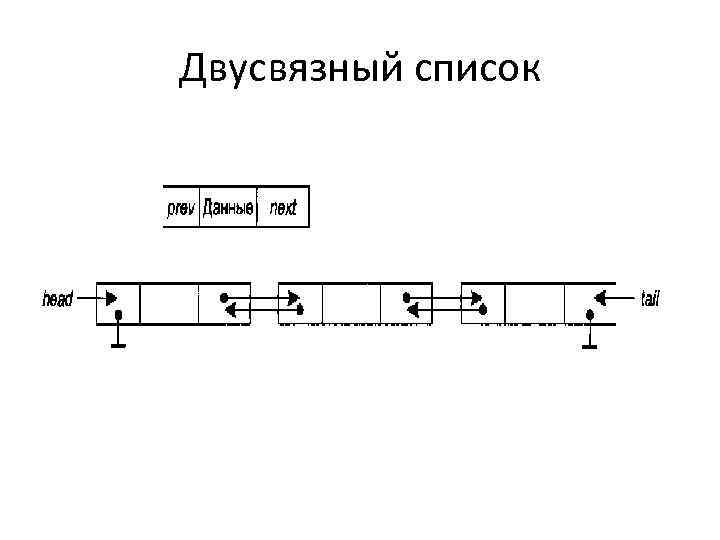Двусвязный список

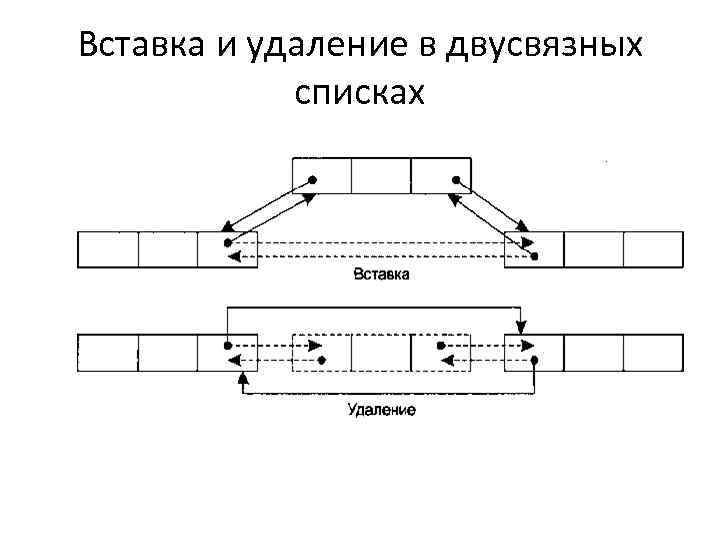Вставка и удаление в двусвязных списках

Обработка данных в виде деревьев • Элементы данных могут образовывать и более сложные структуры, чем линейный список. • Часто данные, подлежащие обработке, образуют иерархическую структуру, которую необходимо отобразить в памяти компьютера и, соответственно, описать в структурах данных. • Такая структура получила название дерева. Каждый элемент такой структуры, называемый узлом, может содержать ссылки на элементы более низкого уровня иерархии, а может быть, и на объект, находящийся на более высоком уровне иерархии. • Узел, находящийся на самом верхнем уроне иерархии, называется корневым.

Корень дерева • это единственный узел, не имеющий непосредственного предка. • Имеется множество типов деревьев. Важнейшим с точки зрения информатики подмножеством структуры типа дерева является подмножество бинарных деревьев поиска. • У бинарного дерева каждый узел имеет не более двух дочерних узлов, причем левый и правый узлы различаются. • Каждый узел содержит несколько полей: поля значения, хранящегося в узле, и полей, указывающих на левый и правый потомки данного узла, а также на родительский узел.

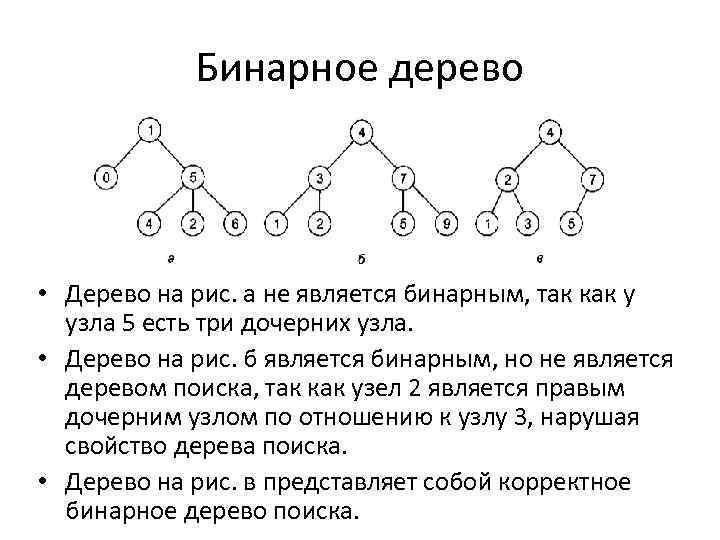Бинарное дерево • Дерево на рис. а не является бинарным, так как у узла 5 есть три дочерних узла. • Дерево на рис. б является бинарным, но не является деревом поиска, так как узел 2 является правым дочерним узлом по отношению к узлу 3, нарушая свойство дерева поиска. • Дерево на рис. в представляет собой корректное бинарное дерево поиска.

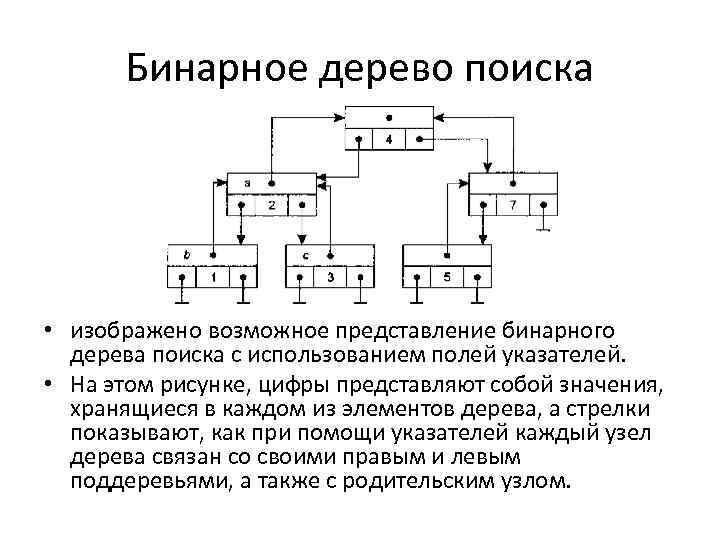Бинарное дерево поиска • изображено возможное представление бинарного дерева поиска с использованием полей указателей. • На этом рисунке, цифры представляют собой значения, хранящиеся в каждом из элементов дерева, а стрелки показывают, как при помощи указателей каждый узел дерева связан со своими правым и левым поддеревьями, а также с родительским узлом.

Обработка данных в виде графов • Графы формально описывают множество близких ситуаций. • Самым привычным примером служит карта автодорог, на которой изображены перекрестки и связывающие их дороги. • Перекрестки являются вершинами графа, а дороги — его ребрами. • Графы могут быть ориентированы (подобно улицам с односторонним движением) или взвешены, когда каждой дороге приписана стоимость путешествия по ней (если, например, дороги платные).

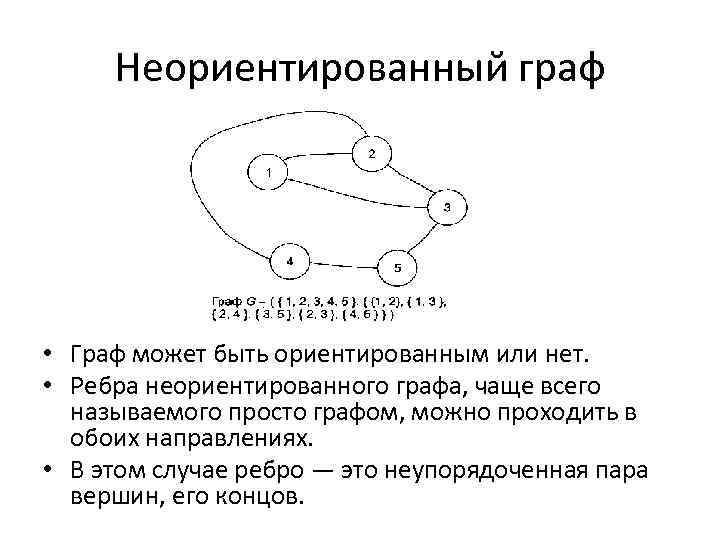Неориентированный граф • Граф может быть ориентированным или нет. • Ребра неориентированного графа, чаще всего называемого просто графом, можно проходить в обоих направлениях. • В этом случае ребро — это неупорядоченная пара вершин, его концов.

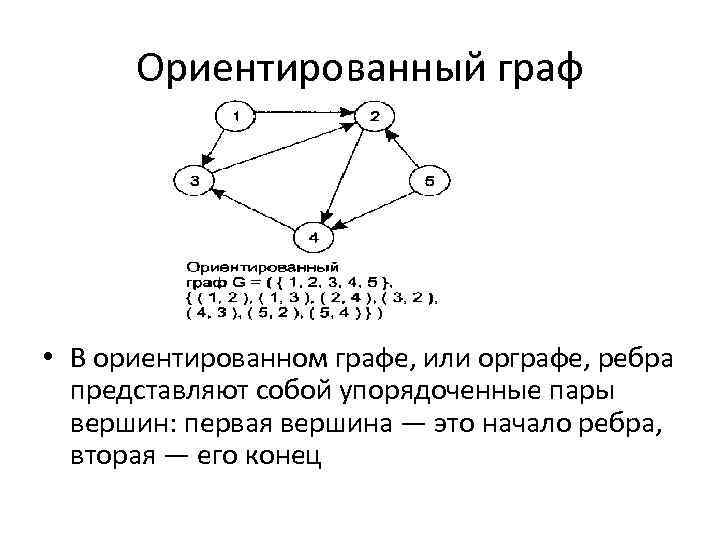Ориентированный граф • В ориентированном графе, или орграфе, ребра представляют собой упорядоченные пары вершин: первая вершина — это начало ребра, вторая — его конец

Полный граф • это граф, в котором каждая вершина соединена со всеми остальными. • Количество ребер в полном графе без петель с N вершинами равно (N 2 - N)/2. • В полном ориентированном графе разрешается переход из любой вершины в любую другую. Поскольку в графе переход по ребру разрешается в обоих направлениях.

Работа с графом • При работе с графами часто приходится выполнять некоторое действие по одному разу с каждой из вершин графа, например, когда некоторую порцию информации следует передать каждому из компьютеров в сети. При этом нерационально посещать какой-либо компьютер дважды. • Аналогичная ситуация возникает, если нужно собирать, а не распространять информацию. • Подобный обход можно совершать двумя способами. При обходе в глубину проход по выбранному пути осуществляется настолько глубоко, насколько это возможно, а при обходе по уровням происходит равномерное движение вдоль всех возможных направлений.

Обход в глубину • При обходе в глубину происходит посещение первого узла, а затем передвижение вдоль ребер графа, пока не будет достигнут тупик. Узел неориентированного графа является тупиком, если уже посещены все примыкающие к нему узлы. В ориентированном графе тупиком также оказывается узел, из которого нет выходящих ребер. • После попадания в тупик следует вернуться назад вдоль пройденного пути, пока не будет обнаружена вершина, у которой есть еще не посещенный сосед, а затем двигаться в новом направлении. Процесс оказывается завершенным после того, как произошел возврат в отправную точку, а все примыкающие к ней вершины уже посещены

Обход по уровням • При обходе графа по уровням после посещения первого узла происходит обход всех соседних с ним вершин. • При втором проходе посещаются все вершины на расстоянии «двух ребер» от начальной. • При каждом новом проходе обходятся вершины, расстояние от которых до начальной на единицу больше предыдущего. • В графе могут быть циклы, поэтому не исключено, что одну и ту же вершину можно соединить с начальной двумя различными путями. • При обходе этой вершины впервые проходится самый короткий до нее путь, и посещать ее второй раз нет необходимости. Поэтому, чтобы предупредить повторное посещение, приходится либо вести список посещенных вершин, либо сопоставить каждой вершине флажок, указывающий, посещена она или нет.

Алгоритмы сортировки и поиска • Известны следующие распространенные методы сортировки: • сортировка вставками; • пузырьковая сортировка; • сортировка Шелла; • корневая сортировка; • пирамидальная сортировка; • сортировка слиянием; • быстрая сортировка.

Сортировка вставками • Основная идея сортировки вставками состоит в том, что при добавлении нового элемента в уже отсортированный список его сразу вставляют в нужное место вместо того, чтобы вставлять его в произвольное место, а затем заново сортировать весь список. • При сортировке вставками первый элемент любого списка считается отсортированным списком длины 1. • Двухэлементный отсортированный список создается добавлением второго элемента исходного списка в нужное место одноэлементного списка, содержащего первый элемент. • После этого можно вставить третий элемент исходного списка в отсортированный двухэлементный список. • Этот процесс повторяется до тех пор, пока все элементы исходного списка не окажутся в расширяющейся отсортированной части списка.

Пузырьковая сортировка • В алгоритме пузырьковой сортировки совершается несколько проходов по списку. При каждом проходе происходит сравнение соседних элементов. Если порядок соседних элементов неправильный, то они меняются местами. Каждый проход начинается с начала списка. Сперва сравниваются первый и второй элементы, затем — второй и третий, потом — третий и четвертый, и т. д. ; элементы с неправильным порядком в паре переставляются. • При обнаружении на первом проходе наибольшего элемента списка он переставляется со всеми последующими элементами, пока не дойдет до конца списка. Поэтому при втором проходе нет необходимости производить сравнение с последним элементом.

Сортировка Шелла • Суть сортировки Шелла состоит в том, что весь список рассматривается как совокупность перемешанных подсписков. • На первом шаге эти подсписки представляют собой просто пары элементов. • На втором шаге в каждой группе оказывается по четыре элемента. При повторении процесса количество элементов в каждом подсписке увеличивается, а количество подсписков, соответственно, падает.

Корневая сортировка • При корневой сортировке упорядочивание списка происходит без непосредственного сравнения ключевых значений между собой. • При этом создается набор «стопок» , а элементы распределяются по стопкам в зависимости от значений ключей. • Собрав значения обратно и повторив всю процедуру для последовательных частей ключа, можно получить отсортированный список. • Чтобы такая процедура работала, распределение по стопкам и последующую сборку следует выполнять очень аккуратно.

Пирамидальная сортировка • Сортировка начинается с построения пирамиды. При этом максимальный элемент списка оказывается в вершине дерева: ведь потомки вершины обязательно должны быть меньше. • Затем корень записывается последним элементом списка, а пирамида с удаленным максимальным элементом переформировывается. • В результате в корне оказывается второй по величине элемент, он копируется в список, и процедура повторяется, пока все элементы не окажутся возвращенными в список.

Сортировка слиянием • один из распространенных алгоритмов рекурсивной сортировки. • В ее основе лежит замечание, согласно которому слияние двух отсортированных списков выполняется быстро. • Список из одного элемента уже отсортирован, поэтому при сортировке слиянием список разбивается на одноэлементные куски, которые затем постепенно сливаются. • Поэтому вся деятельность заключается в слиянии двух списков.

Быстрая сортировка • один из наиболее популярных алгоритмов рекурсивной сортировки. • При быстрой сортировке после выбора в списке элемента список с его помощью делится на две части. • В первую часть попадают все элементы, меньшие выбранного, во вторую — большие выбранного. • В среднем такая сортировка эффективна, однако в наихудшем случае ее эффективность такая же, как у сортировки вставками и у пузырьковой сортировки.

Поиск • Под алгоритмами поиска понимается процесс просмотра списка в поисках некоторого конкретного элемента, называемого целевым. • При последовательном поиске всегда предполагается, что список не отсортирован, поскольку некоторые алгоритмы на отсортированных списках показывают лучшую производительность. • Обычно поиск производится не просто для проверки того, что нужный элемент в списке имеется, а и для того, чтобы получить данные, относящиеся к этому значению ключа.

Последовательный поиск • В алгоритме последовательного поиска последовательно просматривается по одному элементу списка, начиная с первого, до тех пор, пока не будет найден целевой элемент. • Очевидно, что чем дальше в списке находится конкретное значение ключа, тем больше времени уйдет на его поиск. • Это следует помнить при анализе алгоритма последовательного поиска.

Двоичный поиск • При сравнении целевого значения со средним элементом отсортированного списка возможен один из трех результатов: значения равны, целевое значение меньше элемента списка, целевое значение больше элемента списка. • В первом, и наилучшем, случае поиск завершен. В остальных двух случаях можно отбросить половину списка. • Когда целевое значение меньше среднего элемента, известно, что если оно имеется в списке, то находится перед этим средним элементом. • Когда же оно больше среднего элемента, известно, что если оно имеется в списке, то находится после этого среднего элемента